c4e2f7baea2c62e57c535415445ea7d7.ppt
- Количество слайдов: 23

Alternating-Offers Bargaining under One-Sided Uncertainty on Deadlines Francesco Di Giunta and Nicola Gatti Dipartimento di Elettronica e Informazione Politecnico di Milano, Italy

Summary We game-theoretically study alternating-offers protocol under one-sided uncertain deadlines (exclusively in pure strategies) • Original contributions 1. A method to find (when there are) the pure equilibrium strategies given a natural system of beliefs 2. Proof of non-existence of the equilibrium strategies (in pure strategies) for some values of the parameters
![Principal Works in Incomplete Information Bargaining • Classic (theoretical) literature • [Rubinstein, 1985] A Principal Works in Incomplete Information Bargaining • Classic (theoretical) literature • [Rubinstein, 1985] A](https://present5.com/presentation/c4e2f7baea2c62e57c535415445ea7d7/image-3.jpg)
Principal Works in Incomplete Information Bargaining • Classic (theoretical) literature • [Rubinstein, 1985] A bargaining model with incomplete information about time preferences • No deadlines (uncertainty over discount factors) • [Chatterjee and Samuelson, 1988] Bargaining under two-sided incomplete information: the unrestricted offers case • No deadlines (uncertainty over reservation prices) • Computer science literature • [Sandholm and Vulkan, 1999] Bargaining with deadlines • Non alternating-offers protocol (war-of-attrition refinement) • Continuous time • [Fatima et al. , 2002] Multi-issue negotiation under time constraints • Non perfectly rational agents (negotiation decision function paradigm based agents)
![Revision of Complete Information Solution [Napel, 2002] Revision of Complete Information Solution [Napel, 2002]](https://present5.com/presentation/c4e2f7baea2c62e57c535415445ea7d7/image-4.jpg)
Revision of Complete Information Solution [Napel, 2002]

The Model of the Alternating. Offers with Deadlines • Player function • Actions • Preferences
![Complete Information Solution • • • Equilibrium notion • Subgame Perfect Equilibrium [Selten, 1972], Complete Information Solution • • • Equilibrium notion • Subgame Perfect Equilibrium [Selten, 1972],](https://present5.com/presentation/c4e2f7baea2c62e57c535415445ea7d7/image-6.jpg)
Complete Information Solution • • • Equilibrium notion • Subgame Perfect Equilibrium [Selten, 1972], it defines the equilibrium strategies of any agent in any possible reachable subgame Backward induction • • • The game is not rigorously a finite horizon game However, no rational agent will play after his deadline Therefore, there is a point from which we can build backward induction construction • • We call it the deadline of the bargaining T It is: T = min {Tb, Ts} Solution construction 1. 2. The deadline of the bargaining is determined From the deadline backward induction construction is employed to determine agents’ equilibrium offers and acceptances
![Backward Propagation x 3[b] x x 2[b] x s x b x 2[s] x Backward Propagation x 3[b] x x 2[b] x s x b x 2[s] x](https://present5.com/presentation/c4e2f7baea2c62e57c535415445ea7d7/image-7.jpg)
Backward Propagation x 3[b] x x 2[b] x s x b x 2[s] x t-3 t-2 t-1 t x 3[s] t-3 t-2 t-1 t
![Backward Induction Construction time Tb price RPb Ts Infinite Horizon Construction (RPs) 3[bs]b (RPs) Backward Induction Construction time Tb price RPb Ts Infinite Horizon Construction (RPs) 3[bs]b (RPs)](https://present5.com/presentation/c4e2f7baea2c62e57c535415445ea7d7/image-8.jpg)
Backward Induction Construction time Tb price RPb Ts Infinite Horizon Construction (RPs) 3[bs]b (RPs) 2[bs]b (RPs) bsb (RPs) 3[bs] (RPs) 2[bs] Finite Horizon Construction RPs (seller) (buyer) (seller) (RPs) bs (buyer) RPs (seller) (buyer) (seller)

Equilibrium Strategies • We call x*(t) the offers found by backward induction for each time point t • Equilibrium strategies are expressed in function of x*(t)

One-Sided Uncertainty Over Deadlines Solution (exclusively with pure strategies)

The Model Concerning Uncertain Deadlines • We consider the situation in which buyer’s deadline is uncertain • The seller has an initial belief concerning buyer’s deadline: a finite probability distribution over the buyer’s possible deadlines • Formally:

Equilibrium of a Imperfect Information Extensive Form Game • Assessment (µ, ) • System of beliefs µ that defines the agents’ beliefs in each information set • Equilibrium strategies that defines the agents’ action in each information set • Equilibrium assessment • Equilibrium strategies are sequentially rational given the system of beliefs µ • System of beliefs are somehow “consistent” with equilibrium strategies µ
![Notions of Equilibrium • Weak Sequential Equilibrium (WSE) [Fudenberg and Tirole, 1991] • Consistency Notions of Equilibrium • Weak Sequential Equilibrium (WSE) [Fudenberg and Tirole, 1991] • Consistency](https://present5.com/presentation/c4e2f7baea2c62e57c535415445ea7d7/image-13.jpg)
Notions of Equilibrium • Weak Sequential Equilibrium (WSE) [Fudenberg and Tirole, 1991] • Consistency is given by Bayes consistency on the equilibrium path, nothing can be said off equilibrium path, being Bayes rule not applicable • Sequential Equilibrium (SE) [Kreps and Wilson, 1982] • Provide a criterion to analyse off-equilibrium-path consistency • The consistency is given by the existence of a sequence of completely behavioural assessment that converges to the equilibrium assessment

The Basis of Our Method • The method 1. We fix a (natural) system of beliefs m 2. We use backward induction together with the considered system of beliefs to determine (if there is any) the sequentially rational strategies 3. We prove a posteriori the consistency (of Kreps and Wilson) • The considered system of beliefs • Once a possible deadline Tb, i is expired, it is removed from the seller’s beliefs and the probabilities are normalized by Bayes rule

Backward Induction with m (1) • The time point from which employing backward induction is T = min{ max{Tb, 1, …, Tb, m}, Ts} • Seller’s optimal offer • In complete information, it is the backward propagation of the next buyer’s optimal offer • Under uncertainty, if the next time point is a possible buyer’s deadline, the seller could offer RPb • Seller’s acceptance • In complete information, it is the backward propagation of the seller’s optimal offer • Under uncertainty, as the seller optimal offer could be rejected, she will accept an offer lower than the backward propagation of her optimal offer

Backward Induction with m (2) • Defining • Equivalent price e of an offer x: Us(e, t) = EUs(x, t) • Deadline function d(t): the probability, given at time t according to m, that time t is a deadline for the buyer • We summarize • Seller’s optimal offer: the offer with the highest equivalent price between RPb and the backward propagation of the optimal offer of the buyer at the next time point • Seller’s optimal acceptance: the backward propagation of the equivalent price of the seller’s optimal offer • Expected utilities

price Agent s Acting in a Possible time Deadline of Agent b Tb, e 1 e 3[sb] Tb, l e 2[sb] e sb 0 b e(offer 0 b) = 0·ω + (1 - ω) · (0 b) e sbs e 2[sb]s e e s 0 (seller) Ts (buyer) (seller) (buyer) 0 (seller) (buyer) (seller)
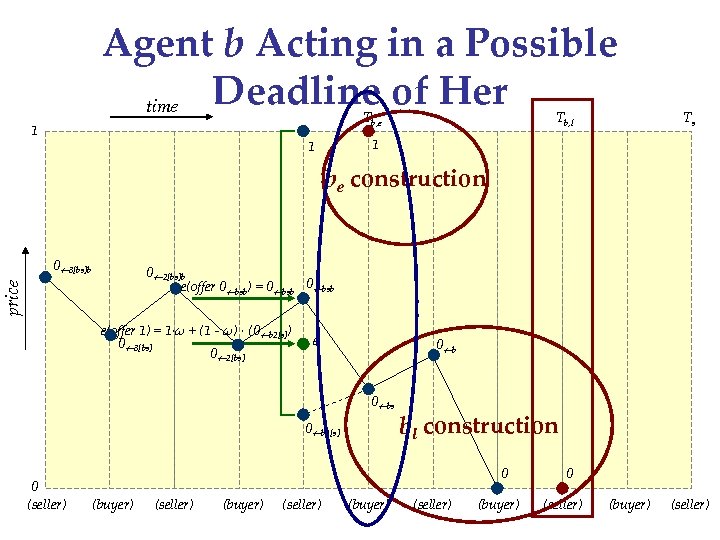
Agent b Acting in a Possible Deadline of Her time Tb, e 1 Tb, l Ts 1 1 be construction 0 3[bs]b price 0 2[bs]b e(offer 0 bsb) = 0 bsb e(offer 1) = 1·ω + (1 - ω) · (0 b 2[s]) 0 3[bs] 0 2[bs] e 0 bs 0 b 2[s] 0 (seller) bl construction 0 (buyer) (seller) (buyer) 0 (seller) (buyer) (seller)
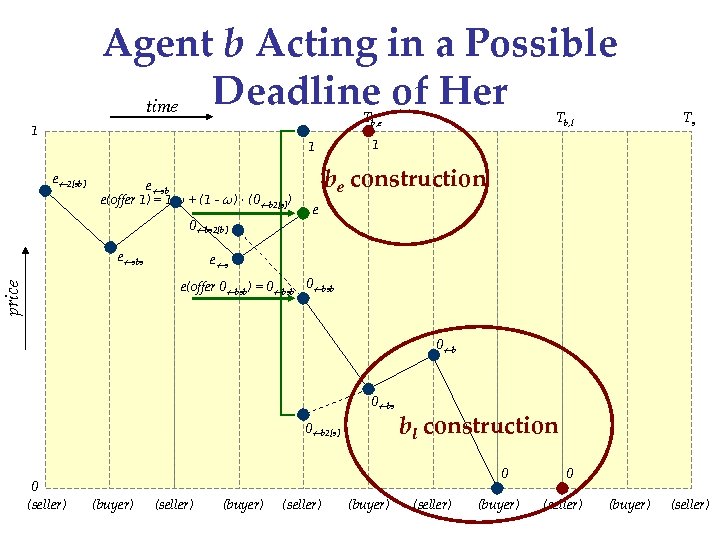
Agent b Acting in a Possible Deadline of Her time Tb, e 1 e sb e(offer 1) = 1·ω + (1 - ω) · (0 b 2[s]) 0 bs 2[b] e sbs Ts 1 1 e 2[sb] Tb, l be construction e e s price e(offer 0 bsb) = 0 bsb 0 bs 0 b 2[s] 0 (seller) bl construction 0 (buyer) (seller) (buyer) 0 (seller) (buyer) (seller)
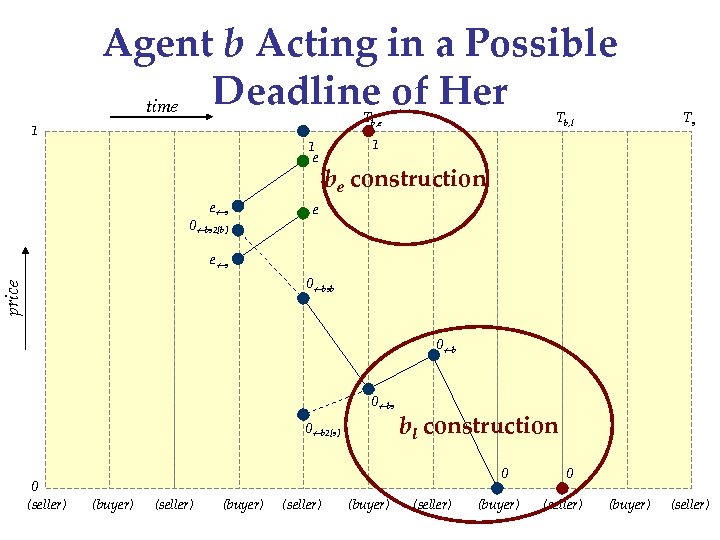
Agent b Acting in a Possible Deadline of Her time Tb, e 1 1 e e s 0 bs 2[b] Tb, l Ts 1 be construction e e s price 0 bsb 0 bs 0 b 2[s] 0 (seller) bl construction 0 (buyer) (seller) (buyer) 0 (seller) (buyer) (seller)

The Equilibrium Assessment • Theorem: If for all t such that i(t)=b holds Us(x*(t 2), t-2) ≥ Us(x*(t), then the considered assessment is a sequential equilibrium • The consistency proof can be derived from the following fully behavioural strategy: • Seller and any buyer’s types before their deadlines: probability (1 -1/n) of performing the equilibrium action, and (1/n) uniformly distributed among the other actions • Buyer’s types after their deadlines: probability (1 -1/n 2) of performing the equilibrium action, and (1/n 2) uniformly distributed among the other actions

Equilibrium Non-Existence Theorem • Theorem: Alternating-offers bargaining with uncertain deadlines does not admit always a sequential equilibrium in pure strategies • The proof reported in the paper • Is (partially) independent from the system of beliefs • Assumes (only) that after a deadline, such a deadline is removed from the seller’s beliefs • It can be proved that the non-existence theorem holds for any system of beliefs, removing the above assumption

Conclusions and Future Works • Conclusions • We have studied the alternating-offers bargaining under one-sided uncertain deadlines • We provide method to find equilibrium pure strategies when they exist • We prove that for some values of the parameters it does not admit any sequential equilibrium in pure strategies • Future works • Introduction of an equilibrium behavioural strategy (which theory assures to exist) to address the equilibrium non-existence in pure strategies • Study of two-sided uncertainty on deadlines and of other kind of uncertainty
c4e2f7baea2c62e57c535415445ea7d7.ppt