Скачать презентацию ALMATY KAZAKH-TURKISH LYCEUM LINES AND PLANES IN SPACE
2-Lesson (LINES AND PLANES IN SPACE).pptx
- Количество слайдов: 16
ALMATY KAZAKH-TURKISH LYCEUM LINES AND PLANES IN SPACE Math Teacher: Kozhahmetov Kuat
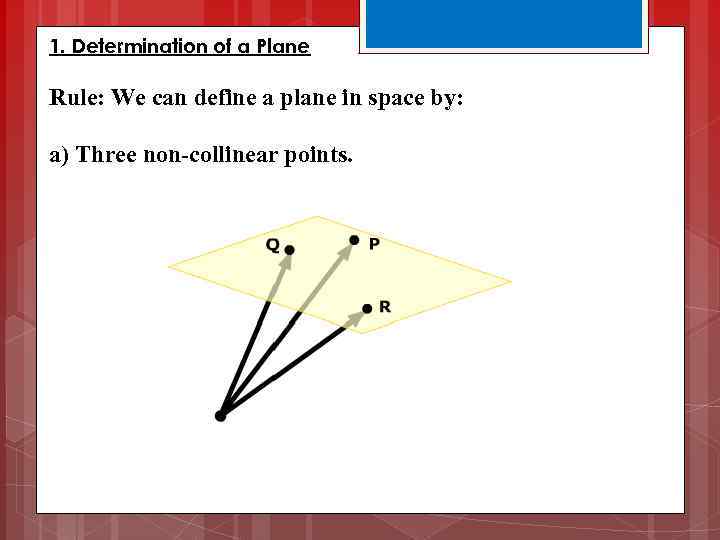1. Determination of a Plane Rule: We can define a plane in space by: a) Three non-collinear points.
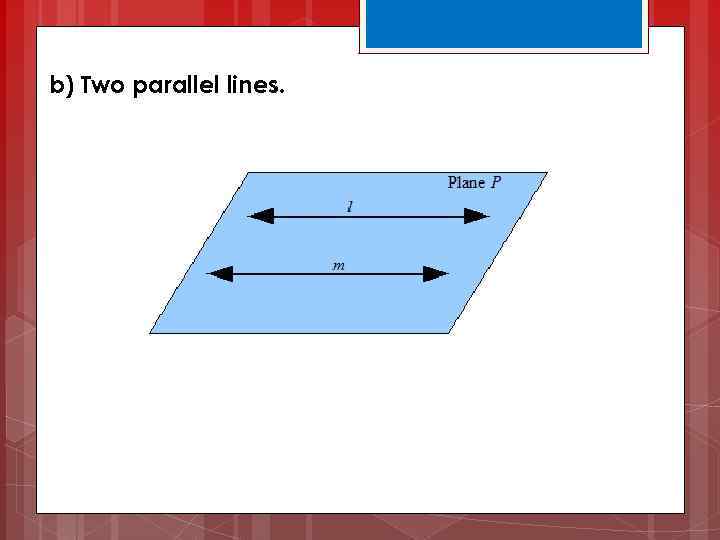b) Two parallel lines.
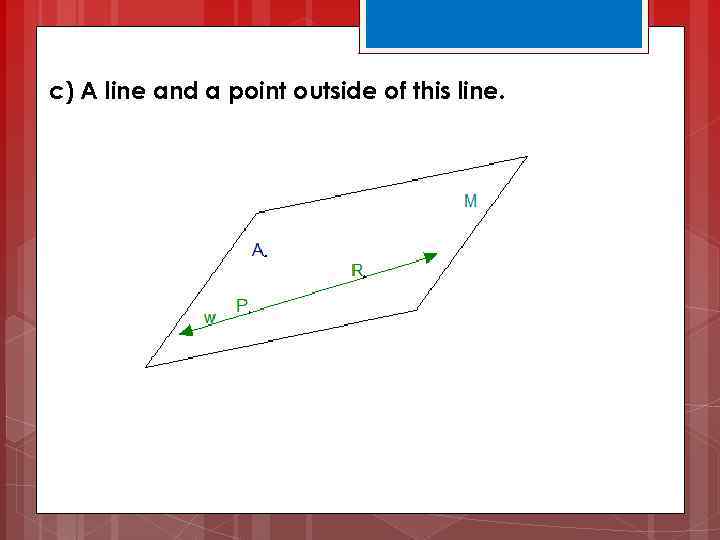c) A line and a point outside of this line.
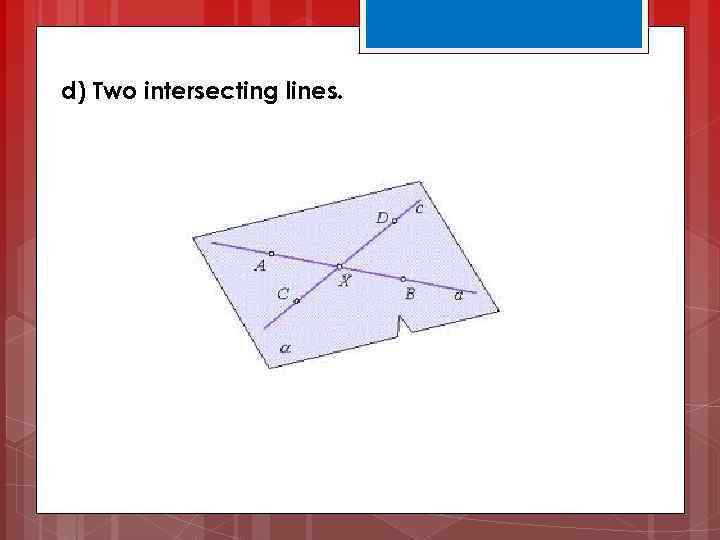d) Two intersecting lines.
Mutual Positions of Two Lines in Space Coincident lines: If two lines are coincident then they have infinitely many intersections. Actually, if two lines have two common points, they are coincident.
One common point: From plane geometry we know that if two lines are intersecting and not coincident then they intersect each other at a unique point. We proved that two intersecting lines determine a plane. So intersecting lines are always coplanar lines.
No common point: If two lines have no common points they may have two conditions: Parallel lines: coplanar Skew lines: Not coplanar
Definition: (Skew Quadrilateral) A quadrilateral whose vertices are four non-coplanar points is called as a skew quadrilateral.
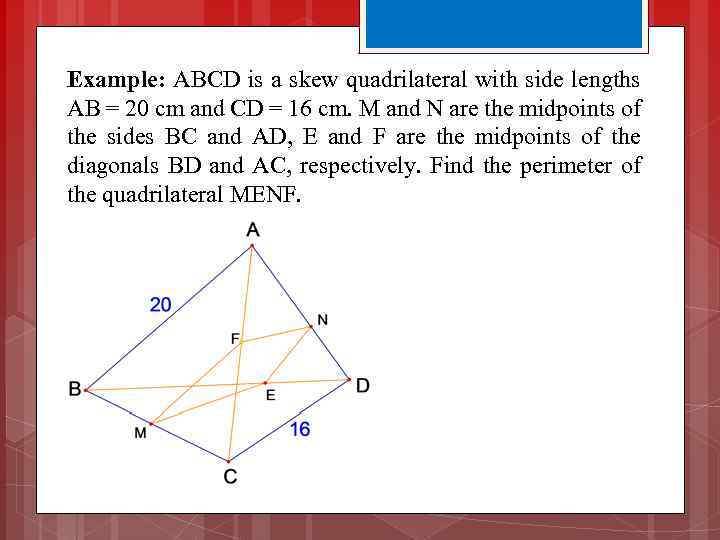Example: ABCD is a skew quadrilateral with side lengths AB = 20 cm and CD = 16 cm. M and N are the midpoints of the sides BC and AD, E and F are the midpoints of the diagonals BD and AC, respectively. Find the perimeter of the quadrilateral MENF.
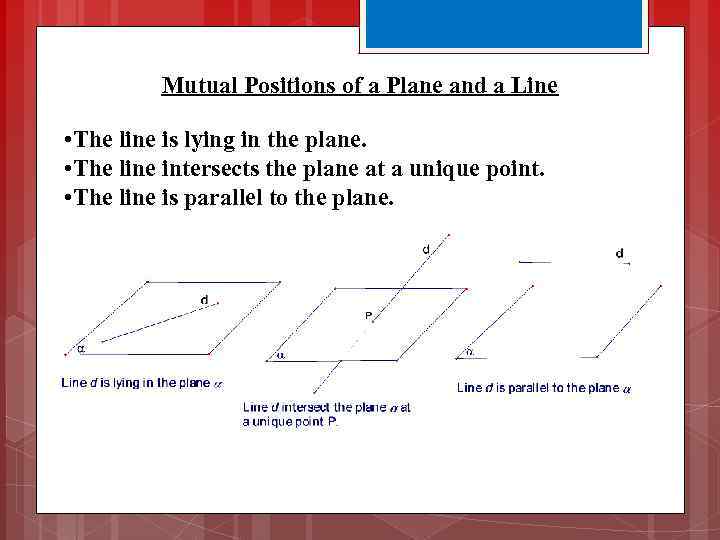Mutual Positions of a Plane and a Line • The line is lying in the plane. • The line intersects the plane at a unique point. • The line is parallel to the plane.
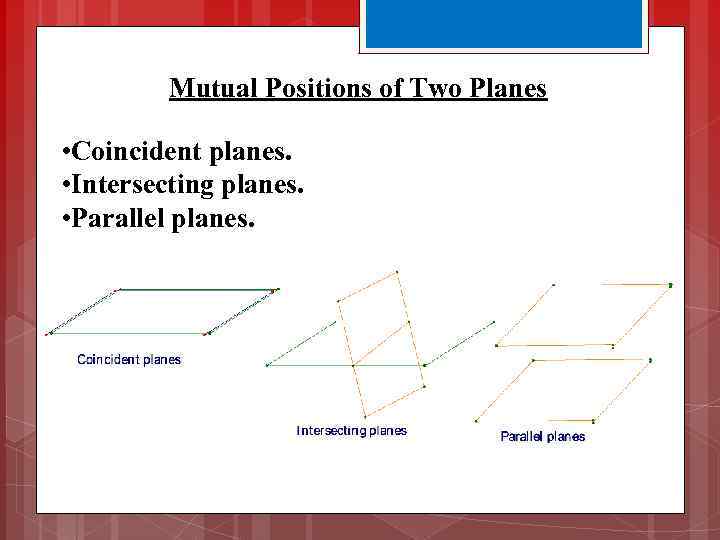Mutual Positions of Two Planes • Coincident planes. • Intersecting planes. • Parallel planes.
HOME WORK: 1. How many planes can be determined by three parallel lines? (Write all possible cases) 2. How many planes can be determined by three intersecting lines? (Write all possible cases) 3. a) From 8 non-collinear points is space how many lines can we draw? b) From 8 non-coplanar points is space how many planes can we draw?
4. State the followings as true or false. a) If lines m and n pass through points M and N, then m and n are coincident. b) If two lines in space have no common point, they are parallel. c) Skew lines can be coplanar or non-coplanar lines. 5. Which of the following figures may not be coplanar? a) triangle b) rhombus c) regular hexagon d) quadrilateral e) circle
