Algorytm uzupełnienia Complement type fr i 21 o

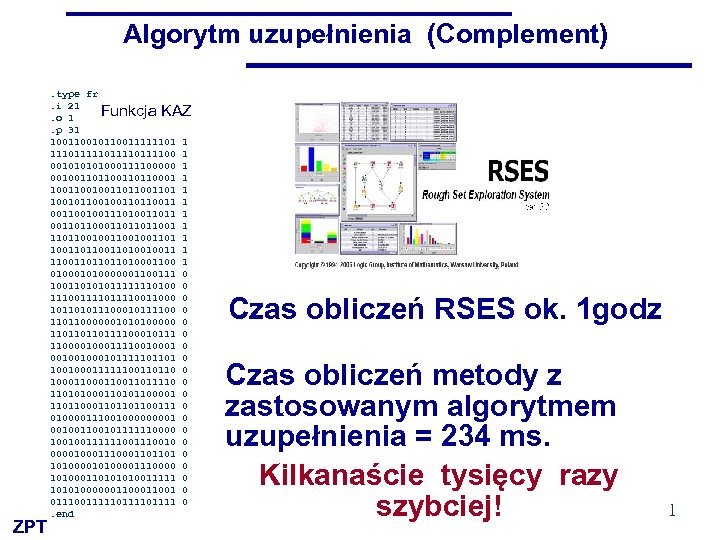Algorytm uzupełnienia (Complement). type fr. i 21. o 1. p 31 100101100111111011110111100 00101000111100000 00100110110001 1001001101101 10010110010011011001100100111010011011011001 110110010011010010011 110011011011010001100 01000101000000111 100110101011111110100 1110011110011000 101101011100010111100 110110000001010100000 110110110111100010111 11000011110010001 00100101111101101 100100011111100110110 1000110011011110 110101000110101100001 110110001101101100111 01000011100100001 00100101111110000 1001001111110010 00001110001101101 10100001110000 10100011010011111 1010100000011001 0111001111101111. end Funkcja KAZ ZPT 1 1 1 0 0 0 0 0 Czas obliczeń RSES ok. 1 godz Czas obliczeń metody z zastosowanym algorytmem uzupełnienia = 234 ms. Kilkanaście tysięcy razy szybciej! 1

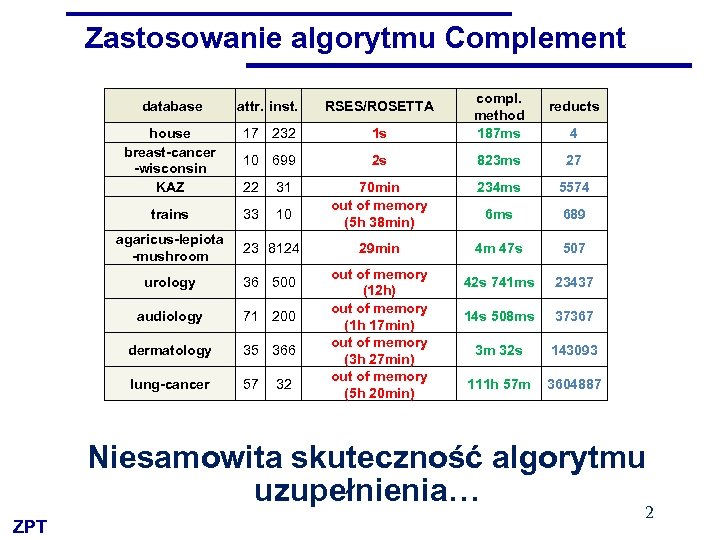Zastosowanie algorytmu Complement database attr. inst. RSES/ROSETTA house breast-cancer -wisconsin KAZ 17 232 1 s compl. method 187 ms 10 699 2 s 823 ms 27 70 min out of memory (5 h 38 min) 234 ms 5574 6 ms 689 29 min 4 m 47 s 507 42 s 741 ms 23437 14 s 508 ms 37367 3 m 32 s 143093 111 h 57 m 3604887 trains 22 31 33 10 agaricus-lepiota -mushroom 23 8124 urology 36 500 audiology 71 200 dermatology 35 366 lung-cancer 57 32 out of memory (12 h) out of memory (1 h 17 min) out of memory (3 h 27 min) out of memory (5 h 20 min) reducts 4 Niesamowita skuteczność algorytmu uzupełnienia… ZPT 2

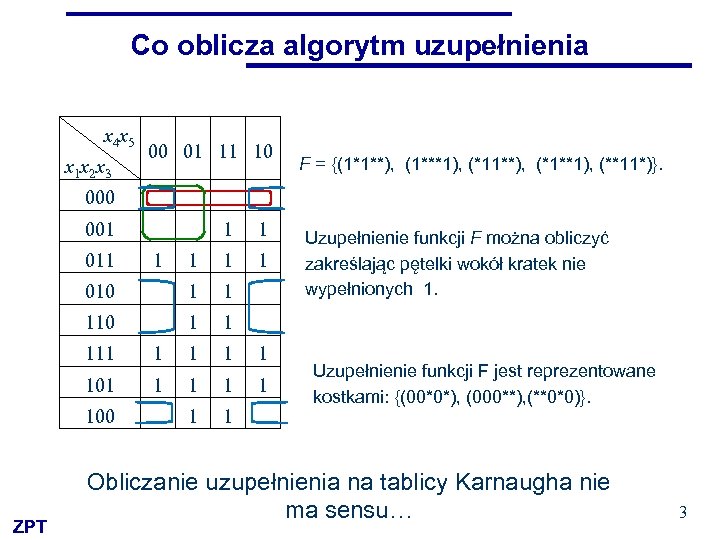Co oblicza algorytm uzupełnienia x 4 x 5 x 1 x 2 x 3 00 01 11 10 F = {(1*1**), (1***1), (*11**), (*1**1), (**11*)}. 000 001 1 1 010 1 1 110 1 1 011 1 101 1 1 1 100 ZPT Uzupełnienie funkcji F można obliczyć zakreślając pętelki wokół kratek nie wypełnionych 1. Uzupełnienie funkcji F jest reprezentowane kostkami: {(00*0*), (000**), (**0*0)}. Obliczanie uzupełnienia na tablicy Karnaugha nie ma sensu… 3

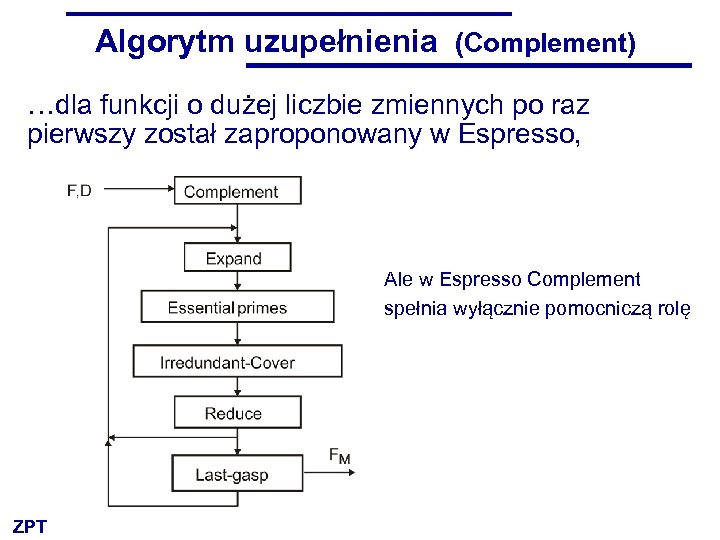Algorytm uzupełnienia (Complement) …dla funkcji o dużej liczbie zmiennych po raz pierwszy został zaproponowany w Espresso, Ale w Espresso Complement spełnia wyłącznie pomocniczą rolę ZPT

Algorytm uzupełnienia (Complement) Sprytna procedura uzupełniania polega na iteracyjnym rozkładzie zbioru kostek reprezentującego funkcję f na kofaktory. Kofaktory te są obliczane tak długo, aż odpowiadające im zbiory kostek staną się „łatwe” do obliczenia ich uzupełnienia. f = Proces kończy „scalanie” wyników cząstkowych. ZPT 5

Complement funkcji jednorodnej Szczególnie prosto oblicza się uzupełnienie funkcji jednorodnej. F = xj F 0 + F 1 Kostki funkcji jednorodnej reprezentuje się binarnie. Uzupełnienie oblicza się dla macierzy M. ZPT 6

Rozkład macierzy M Wybór zmiennej: 1) Wybieramy kostkę (wiersz macierzy M) z największą liczbą zer. 2) W wybranej kostce wybieramy zmienne, które mają jedynkę w tej kostce. 3) Spośród wybranych w punkcie 2) zmiennych wybieramy tę, która ma najwięcej jedynek w swojej kolumnie. ZPT 7

Rozkład macierzy M Obliczanie kofaktorów: Kofaktory macierzy M oblicza się według następującego schematu: Kofaktor jedynkowy macierzy M względem zmiennej xj otrzymujemy przez ustawienie wszystkich pozycji j-tej kolumny macierzy M na zera. Kofaktor zerowy macierzy M względem zmiennej xj otrzymujemy przez wypisanie z M tych kostek (wierszy), w których zmienna xj przyjmuje wartość zero. ZPT 8

Complement kofaktorów Podstawą uzupełnienia funkcji jednorodnej jest rozszczepianie macierzy M na podzbiory kostek, których uzupełnienie łatwo można obliczyć. 1) Jeżeli kofaktor zawiera tylko jedną kostkę, jego uzupełnienie oblicza się wg prawa De Morgana. 2) Jeżeli kofaktor zawiera kostkę (wiersz) samych 0, jego uzupełnienie jest zbiorem pustym. 3) Jeżeli kofaktor jest zbiorem pustym, jego uzupełnienie jest Tautologią. ZPT 9

Scalanie uzupełnionych kofaktorów F = xj F 0 + F 1 Znaczy to, że jeżeli otrzymany kofaktor był zerowy (ozn. F 0), to jego Complement mnożymy przez odpowiednie xj i dodajemy do Complementu kofaktora jedynkowego. ZPT 10

. type fr. i 7. o 1. p 9 1000101 0 1011110 0 1101110 0 1110111 0 0100101 1 1000110 1 1010000 1 1010110 1 1110101 1. e Przykład EXTL Zredukowana macierz porównań 1100000 0010101 0110000 0100001 (x 1 + x 2) (x 3 + x 5 + x 7) (x 2 + x 3) x 2 + x 7) = ( = (x 2 +x 1)(x 2 + x 3)(x 2 + x 7)(x 3 + x 5 + x 7) = =(x 2 +x 1 x 3 x 7)(x 3 + x 5 + x 7) = = x 2 x 3 + x 2 x 5 +x 2 x 7 + x 1 x 3 x 7 {x 4, x 6} {x 2, x 3, x 4, x 6} ZPT {x 2, x 4, x 5, x 6} {x 2, x 4, x 6, x 7} {x 1, x 3, x 4, x 6, x 7} 11

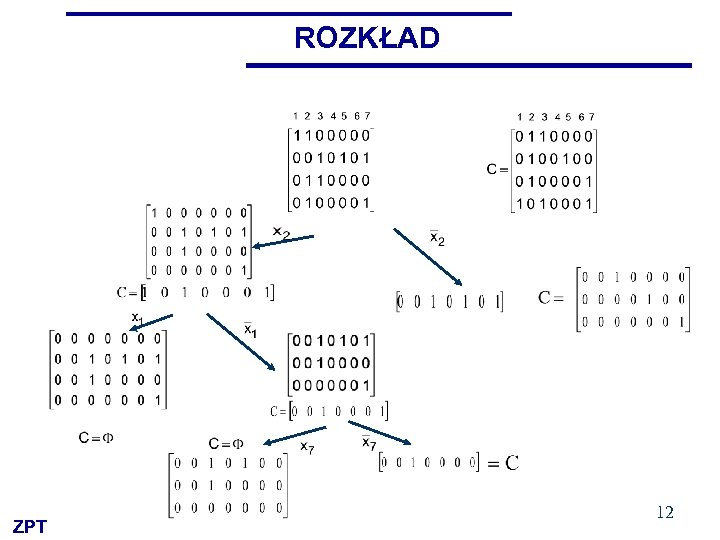ROZKŁAD ZPT 12

SCALANIE C(x 7) = x 7 [0010000]+ = [0010001] C(x 1) = x 1 [0010001]+ = [1010001] C(x 2) = x 2 + [1010001] = Minimalne pokrycia: x 2, x 3, x 2, x 5, x 2, x 7, x 1, x 3, x 7 ZPT Redukty: + x 4, x 6 Dokładnie tak samo jak w metodzie klasycznej! 13

Interpretacja dla funkcji boolowskiej. type fr. i 7. o 1. p 9 1000101 0 1011110 0 1101110 0 1110111 0 0100101 1 1000110 1 1010000 1 1010110 1 1110101 1. e ZPT Zredukowana macierz porównań 1100000 0010101 0110000 0100001 . i 7. o 1. p 6 11 ------1 -1 -1 -11 ----1 -------1. end 1 1 1 reprezentuje funkcję boolowską 14

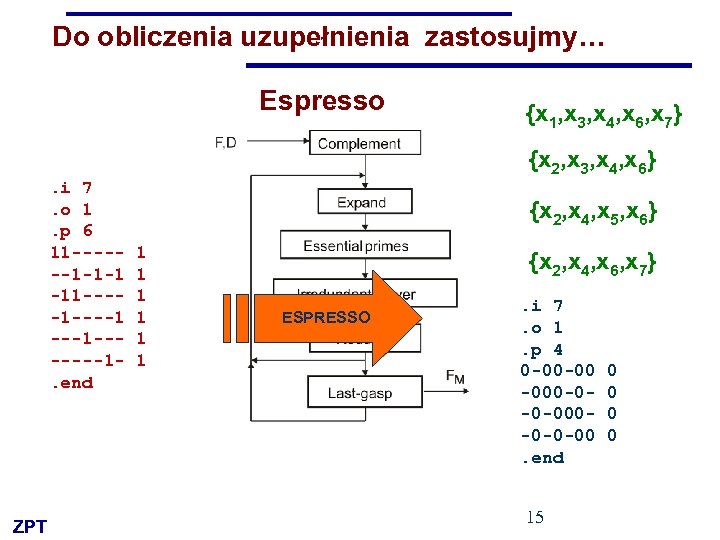Do obliczenia uzupełnienia zastosujmy… Espresso {x 1, x 3, x 4, x 6, x 7} {x 2, x 3, x 4, x 6} . i 7. o 1. p 6 11 ------1 -1 -1 -11 ----1 -------1. end ZPT {x 2, x 4, x 5, x 6} 1 1 1 {x 2, x 4, x 6, x 7} ESPRESSO . i 7. o 1. p 4 0 -00 -00 -000 -0 -0 -00. end 15 0 0

Wnioski w Metoda jest skuteczna w Daje rewelacyjne wyniki w Prosta do implementacji w Jest źródłem ciekawych prac dyplomowych ZPT 16

Konkurs KOMPUTEROWE NARZĘDZIA SYNTEZY LOGICZNEJ Prace dyplomowe Błyskawica (ZIP - 364 k. B) Espresso Pandor Proton (ZIP - 2 947 k. B) Espresso 64 (ZIP - 159 k. B) instant. RS (ZIP - 5 097 k. B) Hummingbird (EXE - 131 k. B) Rough Set Exploration System (ZIP - 3 260 k. B) Downloading Rough Set Exploration System GENERATOR (EXE - 62 k. B) kazmin 1. tab kazmin 2. tab ZPT