АЛГОРИТМЫ ВВЕДЕНИЕ Денис Звонов для ФАЛТ МФТИ http

АЛГОРИТМЫ. ВВЕДЕНИЕ. Денис Звонов для ФАЛТ МФТИ http: //vk. com/algetc

Кто я • Сбербанк-Технологии: руководитель разработки • Дойче Банк: старший разработчик • Выпускник ФАЛТ 2000 • zdv@yahoo. com

Исходники • Amarasinghe, Saman, and Charles Leiserson. 6. 172 Performance Engineering of Software Systems, Fall 2010. (MIT Open. Course. Ware: Massachusetts Institute of Technology), License: Creative Commons BY-NC-SA • Demaine, Erik, and Srinivas Devadas. 6. 006 Introduction to Algorithms, Fall 2011. (MIT Open. Course. Ware: Massachusetts Institute of Technology), License: Creative Commons BY-NC-SA • Leiserson, Charles, and Erik Demaine. 6. 046 J Introduction to Algorithms (SMA 5503), Fall 2005. (MIT Open. Course. Ware: Massachusetts Institute of Technology), License: Creative Commons BY-NC-SA

Исходники • Algorithms, 4 th Edition by Robert Sedgewick and Kevin Wayne • http: //algs 4. cs. princeton. edu/home/ • Используется с разрешения авторов.

Содержание курса • Базовые алгоритмы и их анализ • Современные архитектуры, кэш и его влияние • Параллельные алгоритмы

Оргвопросы • Во сколько начинать? • Как долго продлится? • Если не будут ходить? • Будет ли зачет? • Язык программирования • Умение программировать • Перспективы • Продолжение • http: //vk. com/algetc

Зачем мне это надо • Сопричастность • Результат • Гордость • Связи • Общее дело • Чувство востребованности • Новая/альтернативная область деятельности • Другой уровень знаний • Карма

Зачем вам это надо • Проще, чем изучать самому (но медленнее) • Отобрано важное • Возможность спросить • Общий базис –> возможность обсудить и сделать • Психологический эффект, взгляд на себя • Перспективы обучения • Связи • Диверсификация • Opportunity • Не только IT

АНАЛИЗ АЛГОРИТМОВ Теоретическое исследование производительности компьютерных программ и использования ими ресурсов.

Что важнее производительности? • Модульность • Корректность • Поддерживаемость • Функциональность • Устойчивость • Удобство использования • Время разработки • Простота • Расширяемость • Надежность

Зачем изучать алгоритмы и производительность? • Понимать масштабируемость • Понимать пределы возможностей • Алгоритмы дают язык, на котором говорят о поведении программ • Производительность – это деньги (валюта) IT • Простор для открытий – в алгоритмах и в науках • Стимулирование интеллекта • Профессия • Fun! • Challenge! • Profit!

Зачем изучать что-то другое?

Анализ алгоритмов. • Предсказывать производительность • Сравнивать алгоритмы • Иметь гарантии

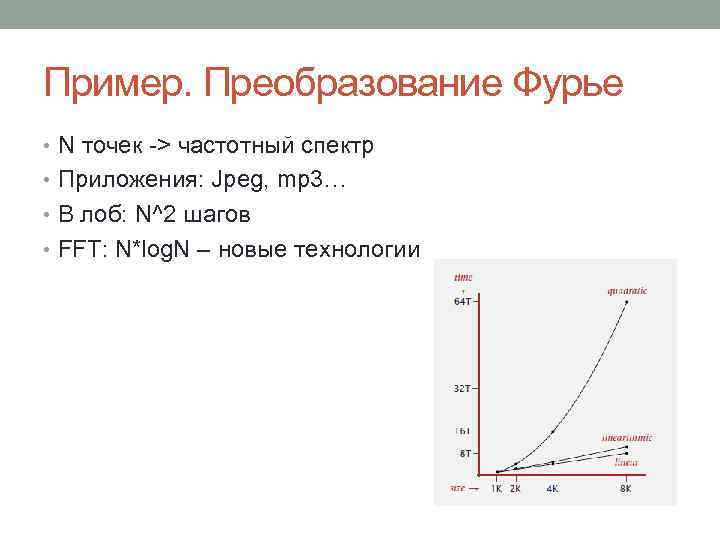Пример. Преобразование Фурье • N точек -> частотный спектр • Приложения: Jpeg, mp 3… • В лоб: N^2 шагов • FFT: N*log. N – новые технологии

Практическая сторона вопроса Сможет ли моя программа решать задачу на реальных входных данных большого объема? Понимание <- научный метод

Научный метод • Наблюдение • Выдвижение гипотезы • Предсказание на базе гипотезы • Проверка предсказаний наблюдениями • Оценка и повторение Принципы: • Эксперимент должен быть повторяемым • Гипотеза должна быть фальсифицируемой

Пример. 3 -sum • Дано: N целых чисел • Вопрос: сколько троек, дающих в сумме 0?

В лоб • • • • public static int count(int[] a) { int N = a. length; int cnt = 0; for (int i = 0; i < N; i++) { for (int j = i+1; j < N; j++) { for (int k = j+1; k < N; k++) { if (a[i] + a[j] + a[k] == 0) { cnt++; } } return cnt; }

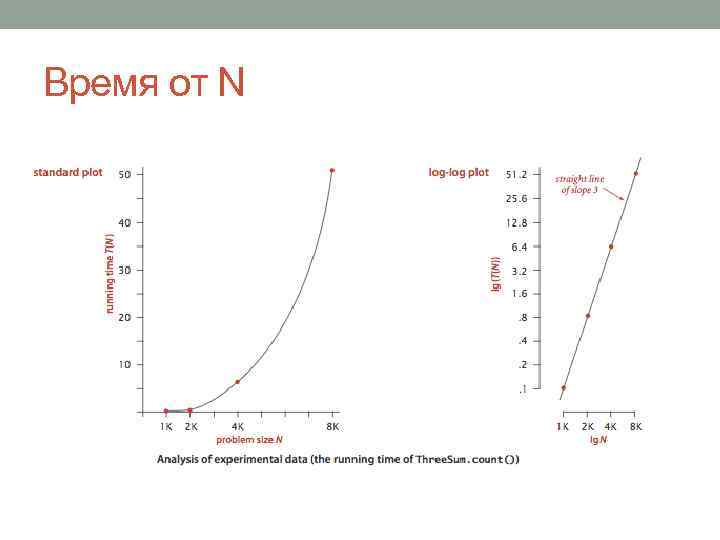Время от N

Бинарный поиск • Дано: сортированный массив целых чисел длиной N • Найти порядковый номер числа k Алгоритм: • Сравнить k с серединой, если ==, то нашли • k меньше -> рассматриваем правую половину • k больше -> рассматриваем левую половину

Количество операций 2 -SUM int cnt = 0; for (int i = 0; i < N; i++) { for (int j = i+1; j < N; j++) if (a[i] + a[j] == 0) { cnt++; } } } 0 + 1 + 2 + … + (N-1) = ?

Количество операций • 3 -SUM int cnt = 0; for (int i = 0; i < N; i++) { for (int j = i+1; j < N; j++) { for (int k = j+1; k < N; k++) { if (a[i] + a[j] + a[k] == 0) { cnt++; } }

Бинарный поиск: код Тривиально? • Впервые опубликовано в 1946 • Первая реализация без ошибок 1962 • Ошибка в Java Arrays. binary. Search() в 2006 • public static int binary. Search(int[] a, int key) { • int low = 0; int high = a. length - 1; • while (low <= high) { • int mid = low + (high - low)/2; • int mid. Val = a[mid]; • if (mid. Val < key) low = mid + 1; • else if (mid. Val > key) high = mid - 1; • else return mid; // key found • } • return -1; // key not found. • }

Бинарный поиск: анализ • T(N) – количество операций сравнения для массива длиной N T(N) <= T(N/2) + 1, если N>1; T(1) = 1 <= T(N/4) + 1 <= T(N/8) + 1 + 1 … <=T(N/N) + 1 + … + 1 =1 + lg. N

3 -SUM: улучшаем • Шаг 1: сортируем входной массив • Шаг 2: Для каждой пары a[i] и a[j], ищем бинарным поиском: –(a[i]+a[j]) Анализ: • Шаг 1: N^2 с самой простой сортировкой • Шаг 2: (N^2)log. N Гипотеза: алгоритм (N^2)log. N гораздо быстрее чем N^3