сортировка_2.pptx
- Количество слайдов: 52

Алгоритмы сортировки Быстрые сортировки

СОРТИРОВКА СЛИЯНИЕМ

Сортировка слиянием Merge sort Алгоритм основан на методе разбиения ( «разделяй и властвуй» ). Сложная задача разбивается на несколько более простых, которые подобны исходной задаче, но имеют меньший объем. Далее эти вспомогательные задачи решаются рекурсивным методом, после чего полученные решения комбинируются с целью получить решение исходной задачи. § массив разбивается на две равные части § обе части массива сортируются методом слияния § две отсортированные части массива сливаются в один упорядоченный массив

Сортировка слиянием Описание алгоритма Mergesort (i, j) if i<j then Mergesort (i, i+(j–i) div 2); Mergesort (i+(j–i) div 2+1, j); Merge (i, j, A); {процедура слияния двух частей массива}
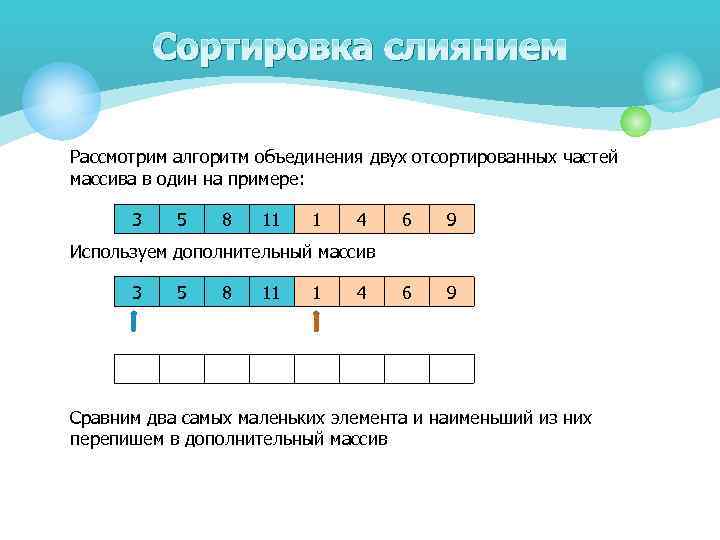
Сортировка слиянием Рассмотрим алгоритм объединения двух отсортированных частей массива в один на примере: 3 5 8 11 1 4 6 9 Используем дополнительный массив 3 5 8 11 1 4 Сравним два самых маленьких элемента и наименьший из них перепишем в дополнительный массив
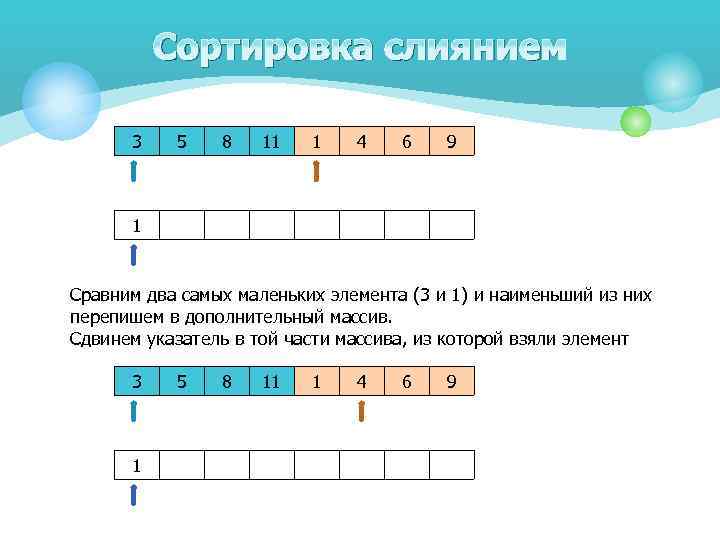
Сортировка слиянием 3 5 8 11 1 4 6 9 1 Сравним два самых маленьких элемента (3 и 1) и наименьший из них перепишем в дополнительный массив. Сдвинем указатель в той части массива, из которой взяли элемент 3 1 5 8 11 1 4 6 9
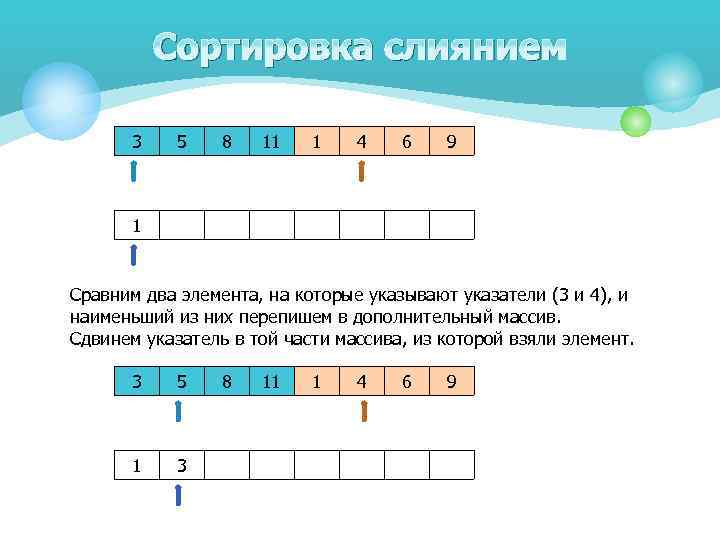
Сортировка слиянием 3 5 8 11 1 4 6 9 1 Сравним два элемента, на которые указывают указатели (3 и 4), и наименьший из них перепишем в дополнительный массив. Сдвинем указатель в той части массива, из которой взяли элемент. 3 5 1 3 8 11 1 4 6 9
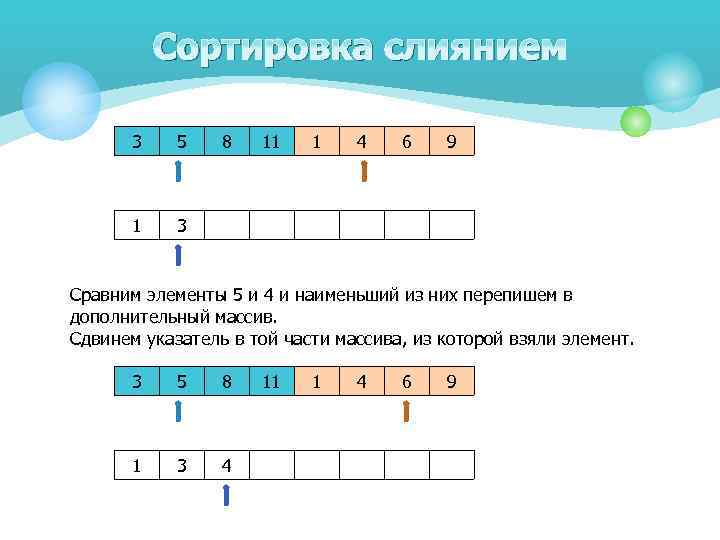
Сортировка слиянием 3 5 1 8 11 1 4 6 9 3 Сравним элементы 5 и 4 и наименьший из них перепишем в дополнительный массив. Сдвинем указатель в той части массива, из которой взяли элемент. 3 5 8 1 3 4 11 1 4 6 9

Сортировка слиянием 3 5 8 1 3 11 1 4 6 9 4 Сравним элементы 5 и 6 и наименьший из них перепишем в дополнительный массив. Сдвинем указатель в той части массива, из которой взяли элемент. 3 5 8 11 1 3 4 5 1 4 6 9
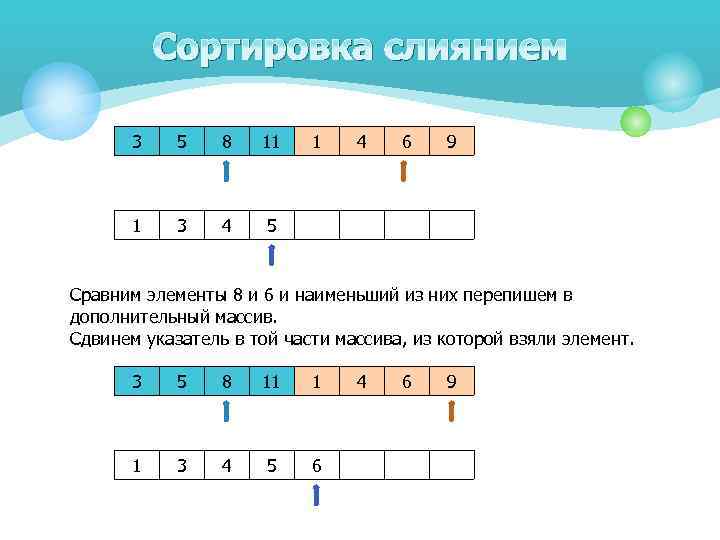
Сортировка слиянием 3 5 8 11 1 3 4 1 4 6 9 5 Сравним элементы 8 и 6 и наименьший из них перепишем в дополнительный массив. Сдвинем указатель в той части массива, из которой взяли элемент. 3 5 8 11 1 1 3 4 5 6 4 6 9
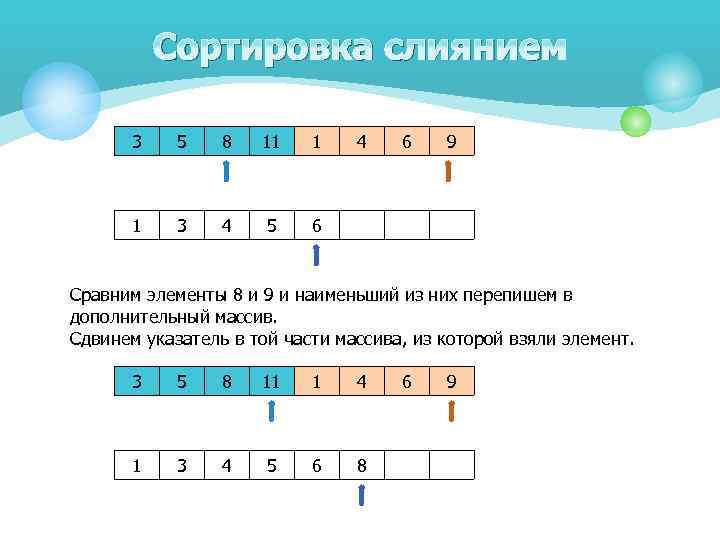
Сортировка слиянием 3 5 8 11 1 1 3 4 5 4 6 9 6 Сравним элементы 8 и 9 и наименьший из них перепишем в дополнительный массив. Сдвинем указатель в той части массива, из которой взяли элемент. 3 5 8 11 1 4 1 3 4 5 6 8 6 9
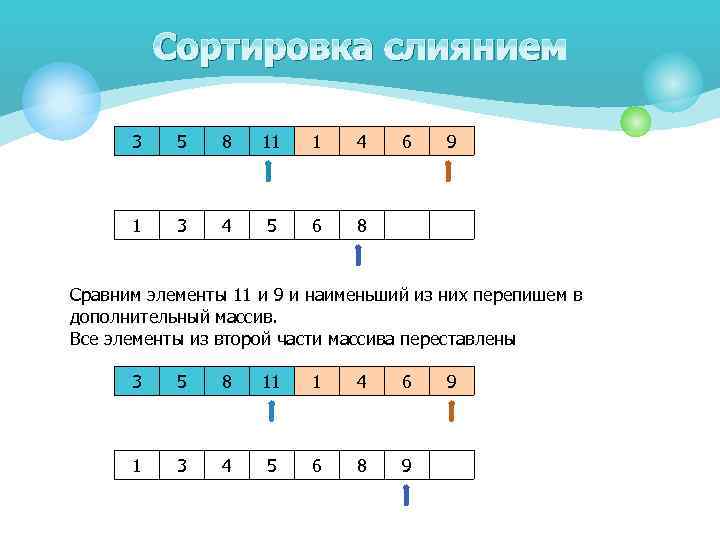
Сортировка слиянием 3 5 8 11 1 4 1 3 4 5 6 6 9 8 Сравним элементы 11 и 9 и наименьший из них перепишем в дополнительный массив. Все элементы из второй части массива переставлены 3 5 8 11 1 4 6 1 3 4 5 6 8 9 9
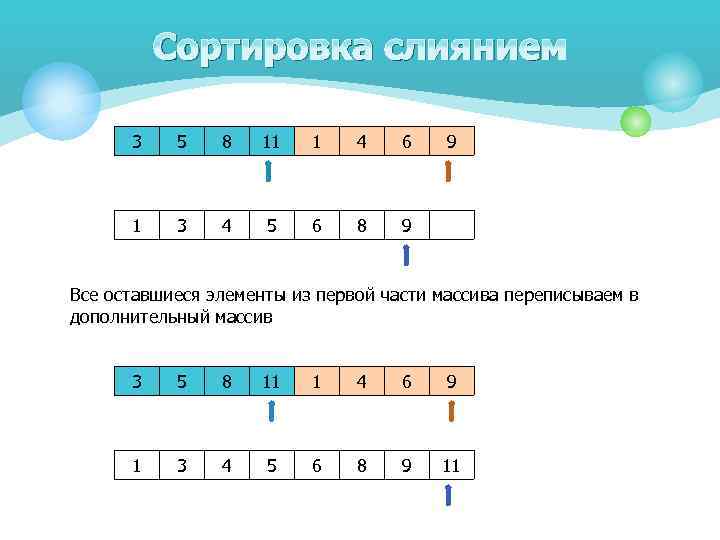
Сортировка слиянием 3 5 8 11 1 4 6 1 3 4 5 6 8 9 9 Все оставшиеся элементы из первой части массива переписываем в дополнительный массив 3 5 8 11 1 4 6 9 1 3 4 5 6 8 9 11
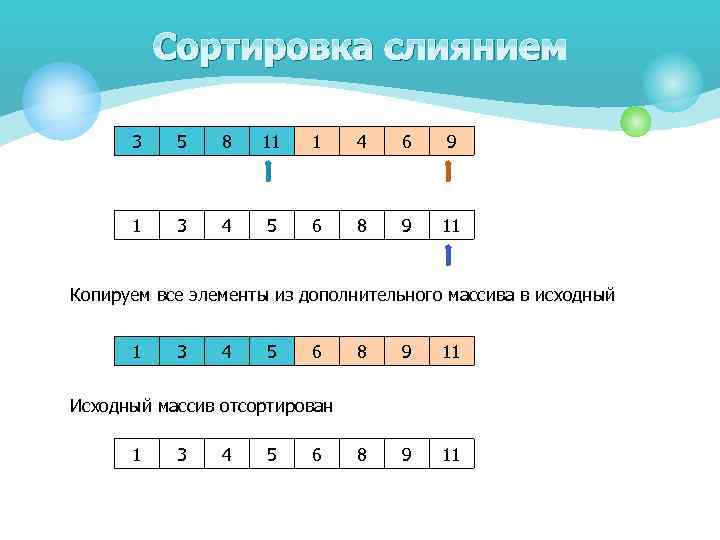
Сортировка слиянием 3 5 8 11 1 4 6 9 1 3 4 5 6 8 9 11 Копируем все элементы из дополнительного массива в исходный 1 3 4 5 6 8 9 11 Исходный массив отсортирован 1 3 4 5 6

Сортировка слиянием Описание алгоритма Mergesort (i, j) if i<j then begin Mergesort (i, i+(j–i) div 2); Mergesort (i+(j–i) div 2+1, j); Merge (i, j, A); {процедура слияния двух частей массива} end;

СОРТИРОВКА ХОАРА

Сортировка Хоара Метод предложен Ч. Э. Р. Хоаром в 1962 г. (QSORT). Алгоритм основан на парадигме «разделяй и властвуй» . В массиве выбирается некоторый элемент (барьерный). Выполняется перестановка элементов массива таким образом, чтобы барьерный элемент встал на свое место, слева находились все элементы меньшие его, справа – большие. Исходный массив теперь разбит на две неупорядоченные части. К обеим частям массива применяется тот же алгоритм до тех пор, пока в каждой из частей не останется по одному элементу.
![Сортировка Хоара Quick sort Массив A[p. . r] разбивается (путем переупорядочения его элементов) на Сортировка Хоара Quick sort Массив A[p. . r] разбивается (путем переупорядочения его элементов) на](https://present5.com/presentation/1/23332036_276003777.pdf-img/23332036_276003777.pdf-18.jpg)
Сортировка Хоара Quick sort Массив A[p. . r] разбивается (путем переупорядочения его элементов) на два подмассива A[p. . q– 1] и A[q+1. . r]. Каждый элемент подмассива A[p. . q– 1] не превышает элемент A[q], а каждый элемент подмассива не меньше элемента A[q]. Индекс q вычисляется в ходе процедуры разбиения. Подмассивы A[p. . q– 1] и A[q+1. . r] сортируются путем рекурсивного вызова процедуры быстрой сортировки. QSort (A, p, r); if p<r then q Partition (A, p, r) {перестановка элементов} Qsort (A, p, q– 1) Qsort (A, q+1, r)
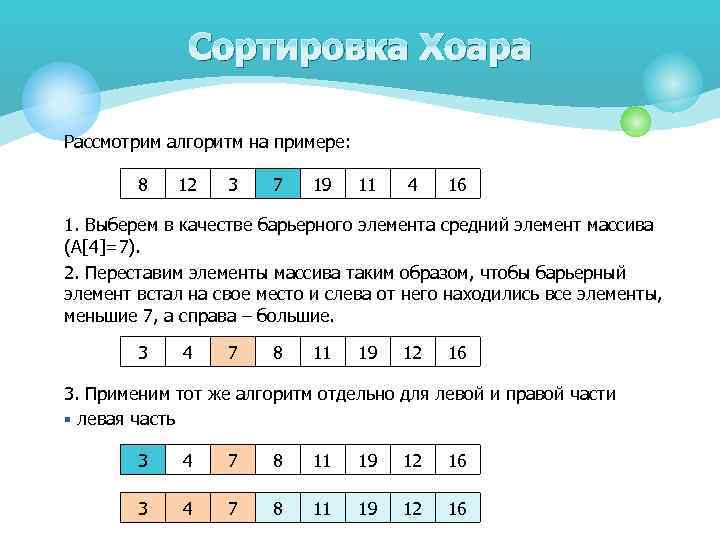
Сортировка Хоара Рассмотрим алгоритм на примере: 8 12 3 7 19 11 4 16 1. Выберем в качестве барьерного элемента средний элемент массива (A[4]=7). 2. Переставим элементы массива таким образом, чтобы барьерный элемент встал на свое место и слева от него находились все элементы, меньшие 7, а справа – большие. 3 4 7 8 11 19 12 16 3. Применим тот же алгоритм отдельно для левой и правой части § левая часть 3 4 7 8 11 19 12 16
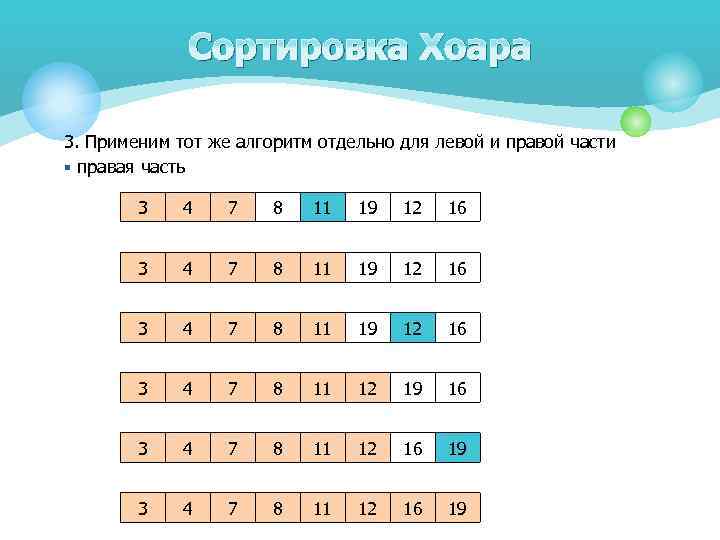
Сортировка Хоара 3. Применим тот же алгоритм отдельно для левой и правой части § правая часть 3 4 7 8 11 19 12 16 3 4 7 8 11 12 19 16 3 4 7 8 11 12 16 19
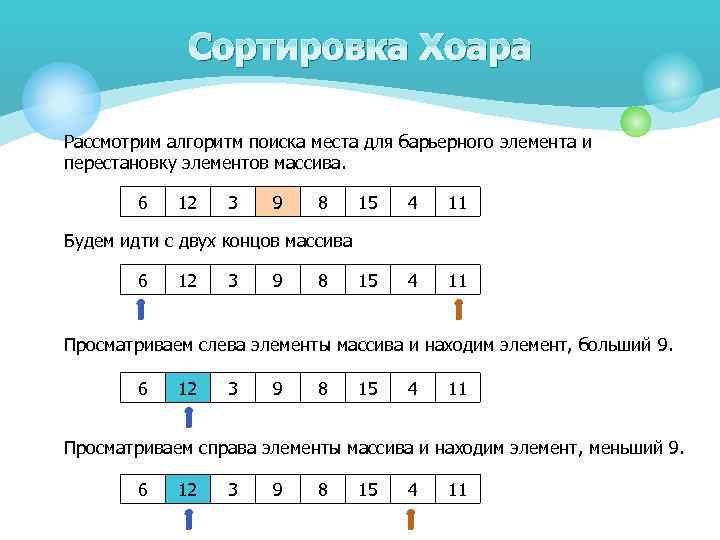
Сортировка Хоара Рассмотрим алгоритм поиска места для барьерного элемента и перестановку элементов массива. 6 12 3 9 8 15 4 11 Будем идти с двух концов массива 6 12 3 9 8 Просматриваем слева элементы массива и находим элемент, больший 9. 6 12 3 9 8 15 4 11 Просматриваем справа элементы массива и находим элемент, меньший 9. 6 12 3 9 8 15 4 11

Сортировка Хоара Переставляем эти элементы (меняем местами) 6 4 3 9 8 15 12 11 Продолжаем эти действия до тех пор, пока указатели не встретятся (их значения не станут равными) 8 6 3 9 8 15 12 16 6 12 3 9 8 15 12 16 9 15 12 16 Меняем элементы местами 6 12 3 8

Сортировка Хоара Переставляем эти элементы (меняем местами) 6 4 3 9 8 15 12 11 Продолжаем эти действия до тех пор, пока указатели не встретятся (их значения не станут равными) 8 6 3 9 8 15 12 16 6 12 3 9 8 15 12 16 9 15 12 16 Меняем элементы местами 6 12 3 8 Применяем алгоритм к левой и правой части массива

ПИРАМИДАЛЬНАЯ СОРТИРОВКА

Пирамидальная сортировка Heap sort Метод предложен Дж. Уильямсом и Р. У. Флойдом в 1964 г. Пирамидальную сортировку еще называют сортировкой «кучей» . Пирамида (binary heap) это структура данных, представляющая собой массив, который можно рассматривать как бинарное дерево.
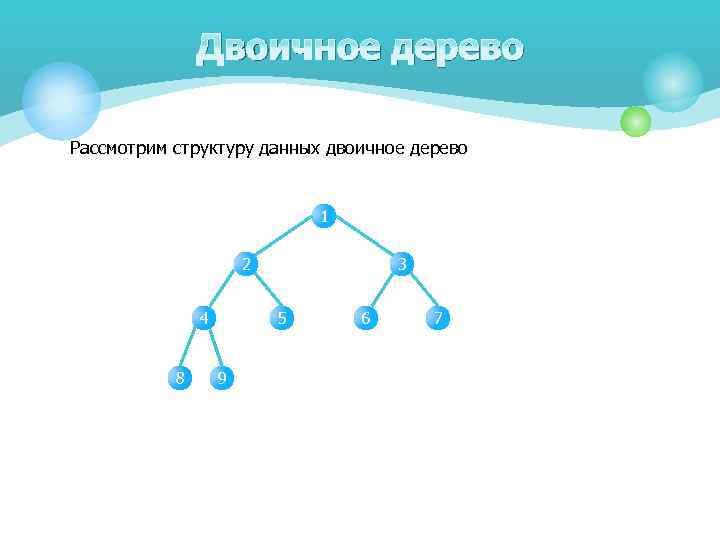
Двоичное дерево Рассмотрим структуру данных двоичное дерево 1 2 4 8 3 5 9 6 7
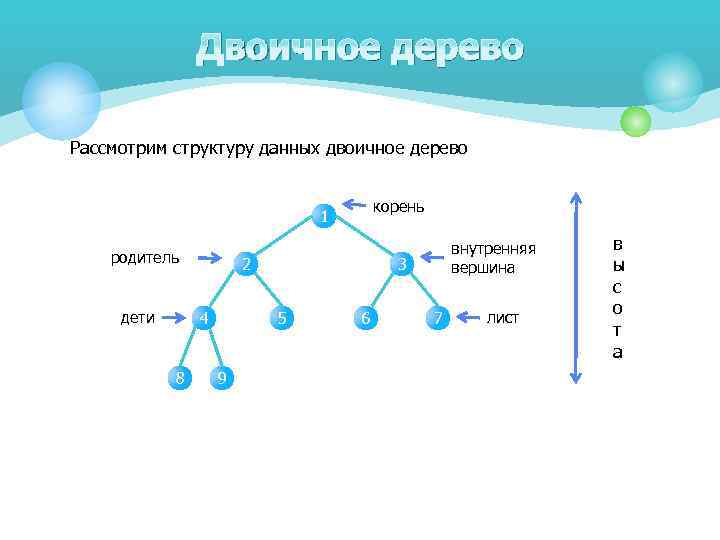
Двоичное дерево Рассмотрим структуру данных двоичное дерево корень 1 родитель дети 2 4 8 3 5 9 внутренняя вершина 6 7 лист в ы с о т а

Двоичное дерево § Корнем дерева называют единственную вершину, находящуюся вверху дерева. § Самые нижние вершины дерева называются листьями. § Вершину называют внутренней, если она не является ни корнем ни листом. § Вершина, которая находится непосредственно над другой вершиной, называется родителем (предком). § Вершина, которая находится непосредственно под другой вершиной, называется ребенком (потомком). § Высота дерева – максимальный уровень какой-либо вершины дерева.

Куча (пирамида) Почти полное двоичное дерево – двоичное дерево с дополнительными условиями: § разница в глубине поддеревьев не более 1; § нижний слой может быть не до конца заполнен. Куча (пирамида) – почти полное двоичное дерево, для всех узлов (вершин) которого выполняется условие: значение ключа родителя меньше значений ключей детей.
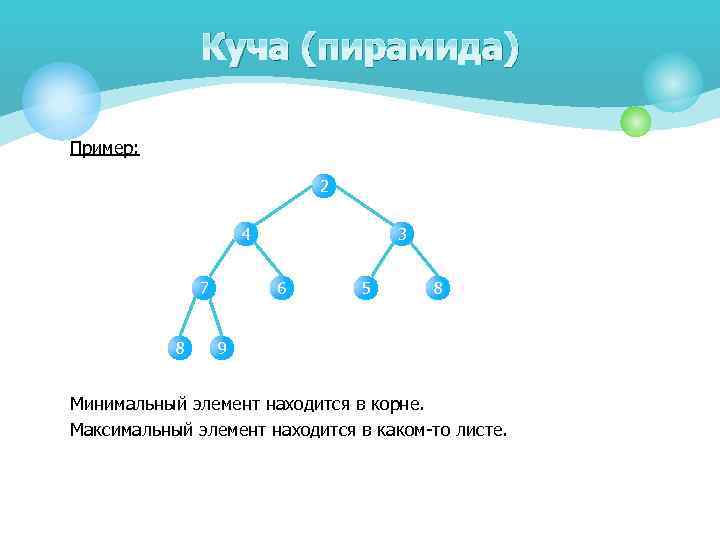
Куча (пирамида) Пример: 2 4 7 8 3 6 5 8 9 Минимальный элемент находится в корне. Максимальный элемент находится в каком-то листе.
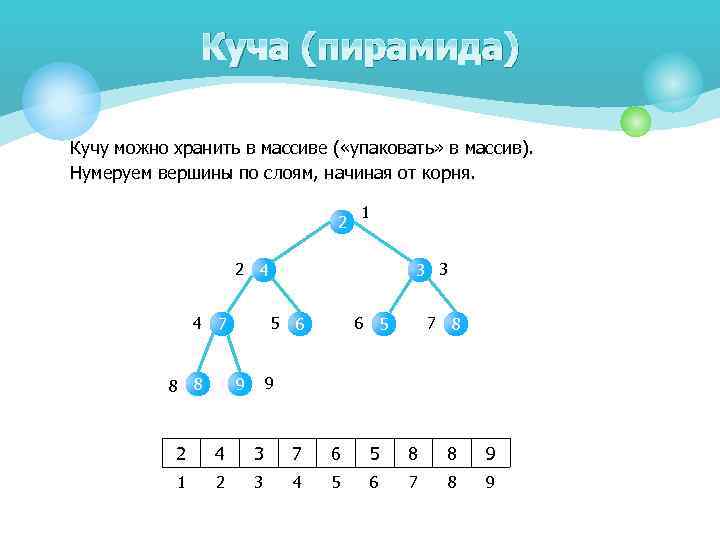
Куча (пирамида) Кучу можно хранить в массиве ( «упаковать» в массив). Нумеруем вершины по слоям, начиная от корня. 2 1 2 4 4 7 8 8 3 3 5 6 6 5 7 8 9 9 2 4 3 7 6 5 8 8 9 1 2 3 4 5 6 7 8 9
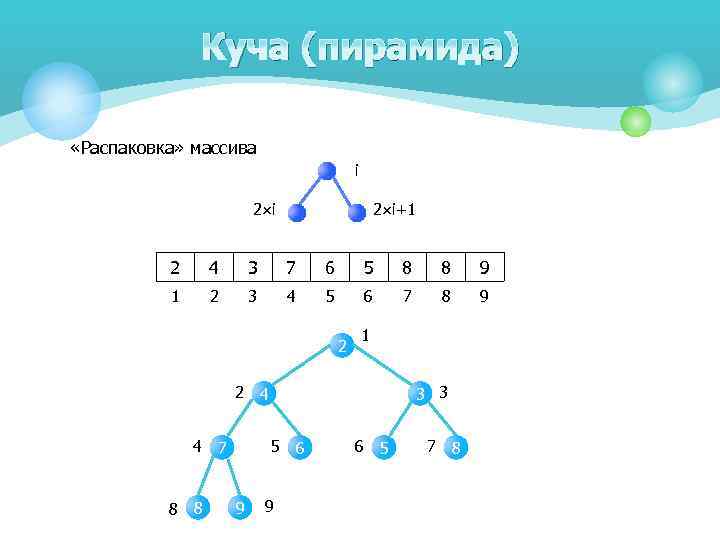
Куча (пирамида) «Распаковка» массива i 2 ×i 2×i+1 2 4 3 7 6 5 8 8 9 1 2 3 4 5 6 7 8 9 2 1 2 4 4 7 8 8 3 3 5 6 9 9 6 5 7 8

Куча (пирамида) Нахождение номера родителя для вершины i div 2 i 2 ×i 2×i+1 Условие кучи: A[i div 2] ≤ A[i]

Основные операции Рассмотрим операции с кучей: § добавление элемента (insert); § извлечение минимального элемента (ex_min).
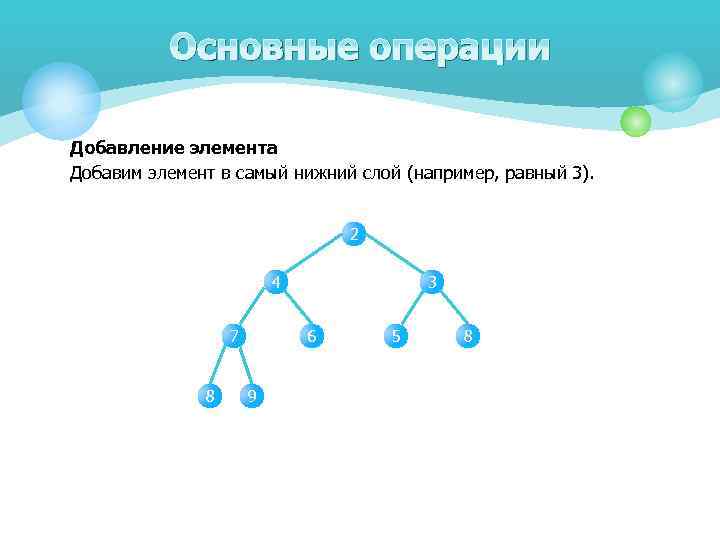
Основные операции Добавление элемента Добавим элемент в самый нижний слой (например, равный 3). 2 4 7 8 3 6 9 5 8
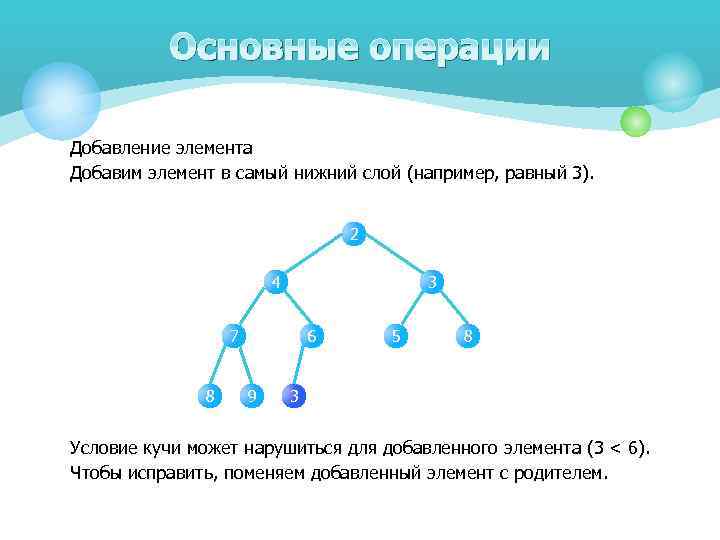
Основные операции Добавление элемента Добавим элемент в самый нижний слой (например, равный 3). 2 4 3 7 8 6 9 5 8 3 Условие кучи может нарушиться для добавленного элемента (3 < 6). Чтобы исправить, поменяем добавленный элемент с родителем.
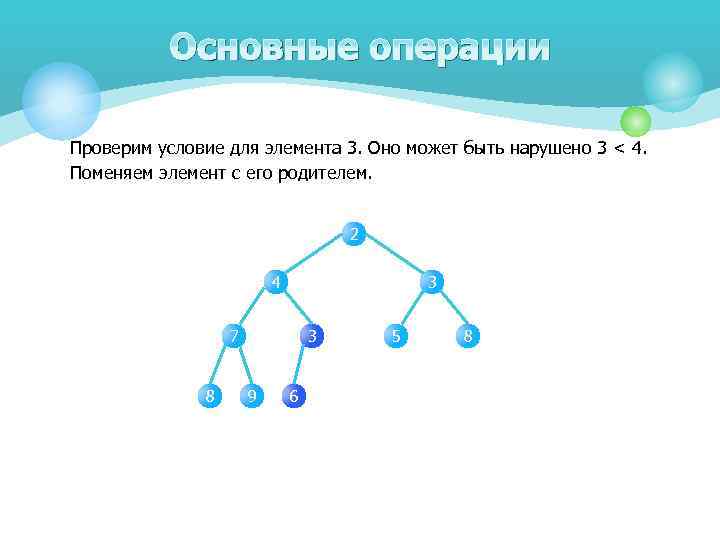
Основные операции Проверим условие для элемента 3. Оно может быть нарушено 3 < 4. Поменяем элемент с его родителем. 2 4 3 7 8 3 9 6 5 8
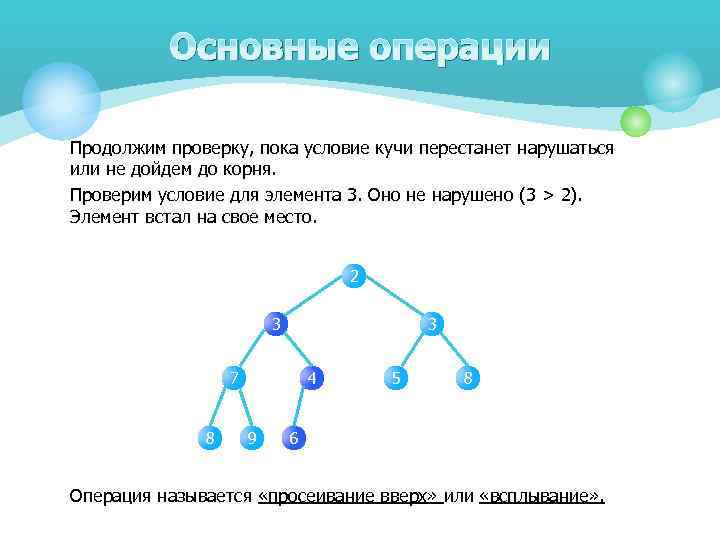
Основные операции Продолжим проверку, пока условие кучи перестанет нарушаться или не дойдем до корня. Проверим условие для элемента 3. Оно не нарушено (3 > 2). Элемент встал на свое место. 2 3 3 7 8 4 9 5 8 6 Операция называется «просеивание вверх» или «всплывание» .
![Основные операции Процедура «просеивание вверх» (siftup) siftup (i); while(i>1) and (A[i div 2]>A[i]) do Основные операции Процедура «просеивание вверх» (siftup) siftup (i); while(i>1) and (A[i div 2]>A[i]) do](https://present5.com/presentation/1/23332036_276003777.pdf-img/23332036_276003777.pdf-39.jpg)
Основные операции Процедура «просеивание вверх» (siftup) siftup (i); while(i>1) and (A[i div 2]>A[i]) do begin A[i] A[i div 2] {обмен} i: =i div 2; end;
![Основные операции Процедура добавления элемента (insert) insert (v); n: =n+1; A[n]: =v; siftup (n); Основные операции Процедура добавления элемента (insert) insert (v); n: =n+1; A[n]: =v; siftup (n);](https://present5.com/presentation/1/23332036_276003777.pdf-img/23332036_276003777.pdf-40.jpg)
Основные операции Процедура добавления элемента (insert) insert (v); n: =n+1; A[n]: =v; siftup (n); {n – количество элементов}
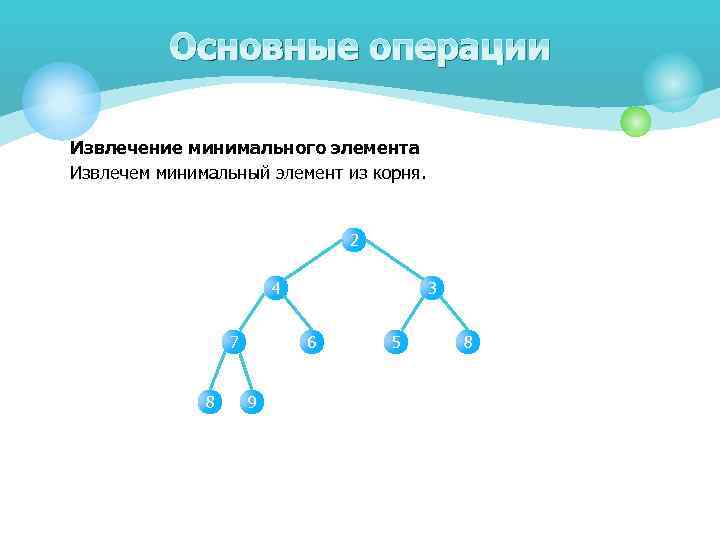
Основные операции Извлечение минимального элемента Извлечем минимальный элемент из корня. 2 4 7 8 3 6 9 5 8
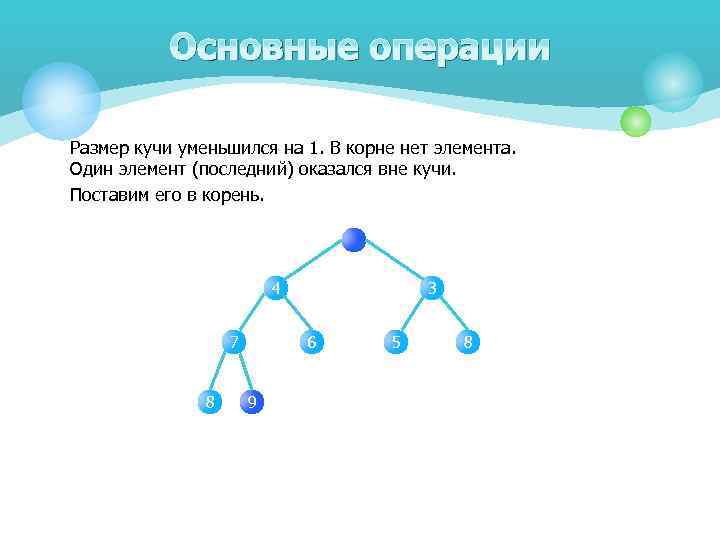
Основные операции Размер кучи уменьшился на 1. В корне нет элемента. Один элемент (последний) оказался вне кучи. Поставим его в корень. 4 7 8 3 6 9 5 8
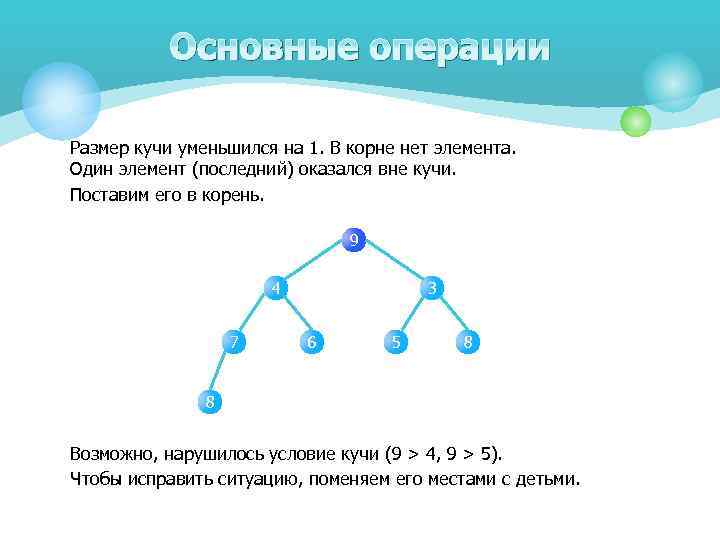
Основные операции Размер кучи уменьшился на 1. В корне нет элемента. Один элемент (последний) оказался вне кучи. Поставим его в корень. 9 4 7 3 6 5 8 8 Возможно, нарушилось условие кучи (9 > 4, 9 > 5). Чтобы исправить ситуацию, поменяем его местами с детьми.
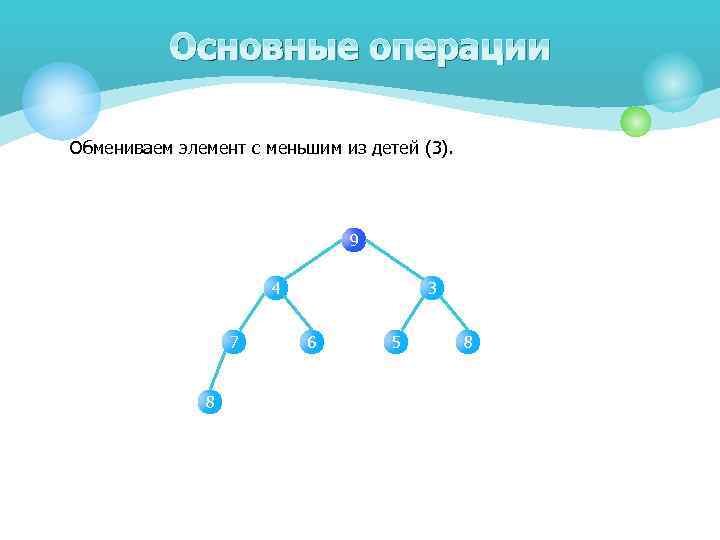
Основные операции Обмениваем элемент с меньшим из детей (3). 9 4 7 8 3 6 5 8
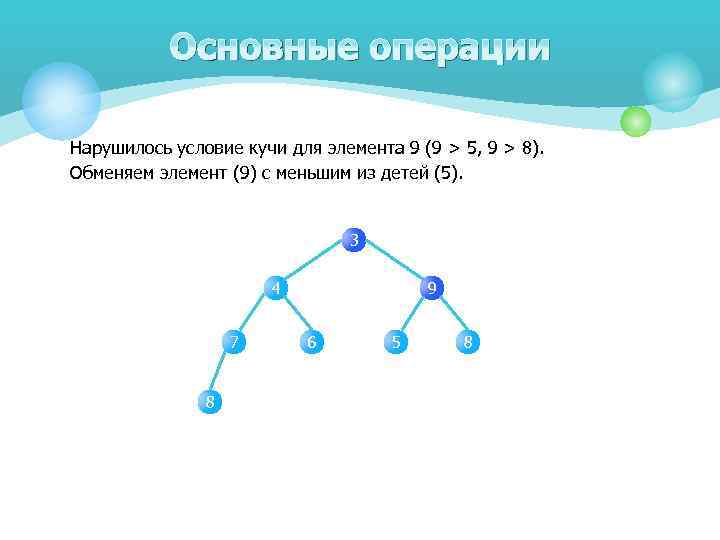
Основные операции Нарушилось условие кучи для элемента 9 (9 > 5, 9 > 8). Обменяем элемент (9) с меньшим из детей (5). 3 4 7 8 9 6 5 8
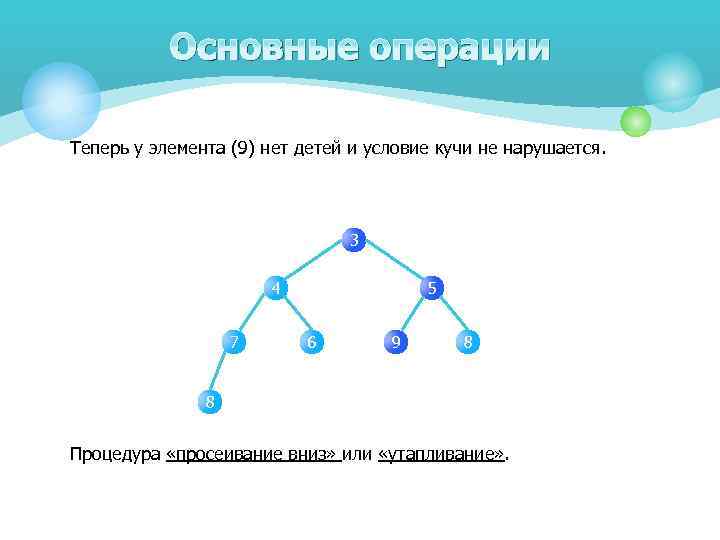
Основные операции Теперь у элемента (9) нет детей и условие кучи не нарушается. 3 4 7 5 6 9 8 8 Процедура «просеивание вниз» или «утапливание» .
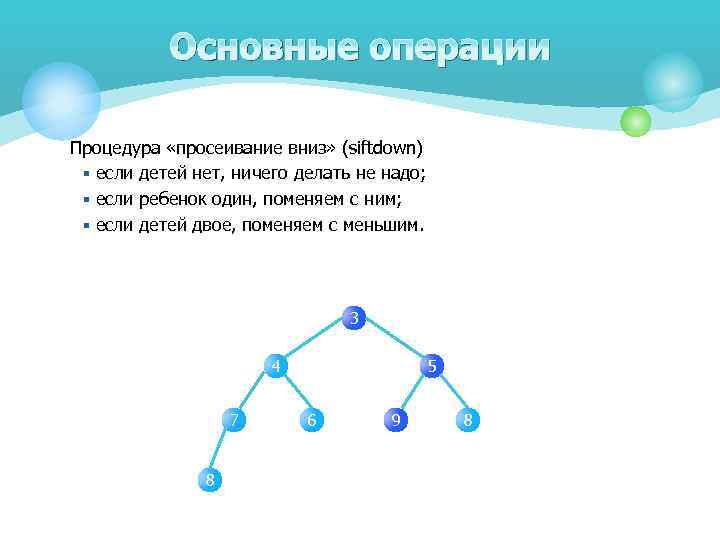
Основные операции Процедура «просеивание вниз» (siftdown) § если детей нет, ничего делать не надо; § если ребенок один, поменяем с ним; § если детей двое, поменяем с меньшим. 3 4 7 8 5 6 9 8

Основные операции Процедура «просеивание вниз» (siftdown) siftdown (i); while (2*i ≤ n) do begin j: =i; { поиск min} if (A[2*i] < A[j]) then j: =2*i; if (2*i+1 ≤ n) and(A[2*i+1] < A[j] then j: =2*i+1; if i=j then break; A[i] A[j]; {обмен} i: =j; end;
![Основные операции Функция извлечения минимального элемента (ex_min) ex_min; ex_min: =A[1]; A[1]: =A[n]; siftdown (1); Основные операции Функция извлечения минимального элемента (ex_min) ex_min; ex_min: =A[1]; A[1]: =A[n]; siftdown (1);](https://present5.com/presentation/1/23332036_276003777.pdf-img/23332036_276003777.pdf-49.jpg)
Основные операции Функция извлечения минимального элемента (ex_min) ex_min; ex_min: =A[1]; A[1]: =A[n]; siftdown (1); {n – количество элементов} Добавление элемента и извлечение минимального элемента работают за log n

Сортировка с помощью кучи Heap sort 1. Для сортировки массива используем дополнительный массив, в котором будем хранить кучу. Создадим кучу, выполнив для всех элементов массива процедуру insert. Извлекая из кучи минимальный элемент и вставляя его в массив, выполним сортировку. куча массив
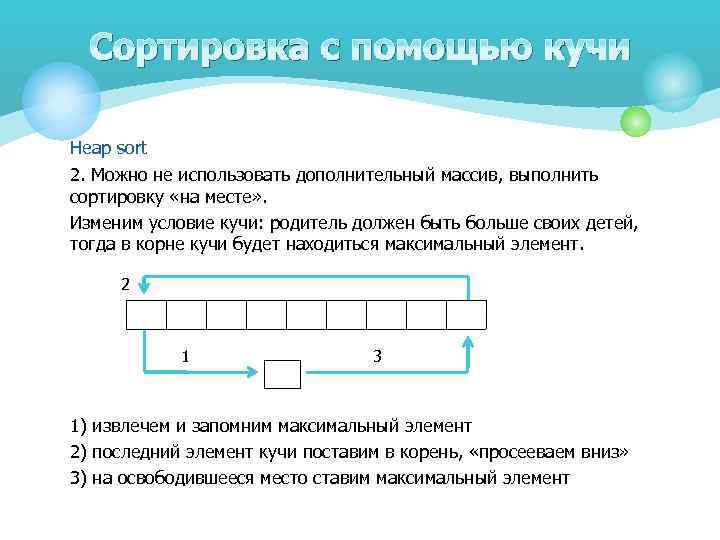
Сортировка с помощью кучи Heap sort 2. Можно не использовать дополнительный массив, выполнить сортировку «на месте» . Изменим условие кучи: родитель должен быть больше своих детей, тогда в корне кучи будет находиться максимальный элемент. 2 1 3 1) извлечем и запомним максимальный элемент 2) последний элемент кучи поставим в корень, «просееваем вниз» 3) на освободившееся место ставим максимальный элемент

Сортировка с помощью кучи Heap sort Построение кучи в массиве 1. Для каждого элемента, начиная с первого, выполним insert, «просеивая вверх» элементы массива. (Время работы log n) 2. Для каждого элемента массива, начиная с последнего и заканчивая первым, выполнить операцию «просеивания вниз» . (Время работы n) for i: = n downto 1 do siftdown (i); Время работы алгоритма сортировки n log n
сортировка_2.pptx