Алгоритмы поиска и сортировки Пропорциональность в композиции

Алгоритмы поиска и сортировки

Пропорциональность в композиции Пропорция – это одно из классических средств композиции, с помощью которого достигается организованность формы Масштаб Пропорция Пропорциональный — значит находящийся в определенном отношении к какой-либо величине Пропорциональные величины — величины, зависящие друг от друга таким образом, что с увеличением одной из них в несколько раз соответственно во столько же раз увеличивается другая величина.

Правило «золотого сечения» соотношение сечения листа 0, 618 к 0, 382 коэффициентами последовательности Фибоначчи

Группа № 18 -11

Сортировка Это процесс перегруппировки заданной последовательности (кортежа) объектов в некотором определенном порядке

Структурированная информация (структура данных) бывает следующего типа : линейная (файл, списки), табличная (числовая матрица), иерархическая (дерево)

Эффективность алгоритма зависит от множества факторов числа сортируемых элементов; степени начальной отсортированности (диапазона и распределения значений сортируемых элементов); необходимости исключения или добавления элементов; доступа к сортируемым элементам (прямого или последовательного).

2 способа доступа к сортируемым данным: Прямой (доступ к любому элементу структуры). Примеры: список, массив Последовательный (доступ к элементу осуществляется, при прохождении всех элементов по очереди) Примеры: файл, стек

Поиск Это процесс нахождения в заданном множестве объекта, обладающего свойствами эталона (образца)

Линейный поиск прямой, последовательный просмотр всех элементов массива данных и сравнение их с некоторым эталоном X. При их совпадении запоминается номер элемента. a 1, a 2, a 3, … , an – задан массив из n элементов; X – это эталон;

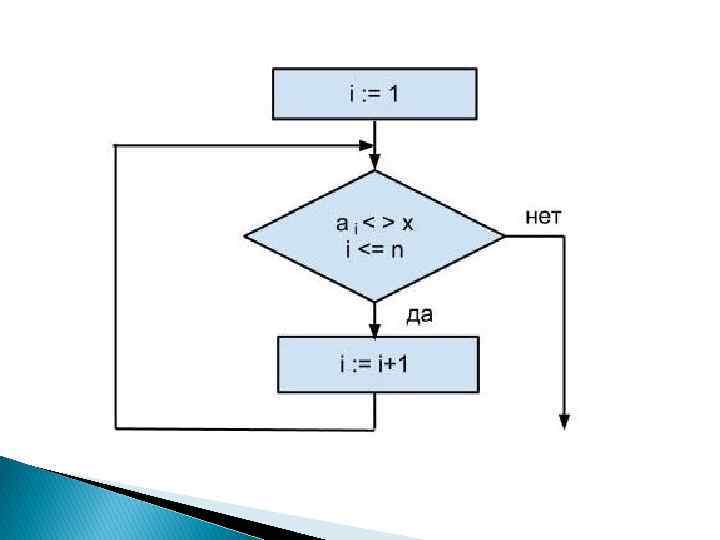
Линейный поиск имеет ряд недостатков: если значение х встречается в массиве несколько раз, то найдено будет последнее из них; после того, как нужное значение уже найдено, массив просматривается до конца, то есть всегда выполняется N сравнений

Поиск с барьером Вводится дополнительно граничный элемент массива a[N+l] При таком способе поиска в случае наличия в массиве нескольких элементов, удовлетворяющих заданному свойству, будет также найден элемент с наименьшим номером (обязательно найдём X элемент).

Поиск делением пополам Применяется тогда, когда массив упорядочен (телефонный справочник, библиотечные каталоги и пр. ) Сравнение эталона х осуществляется с элементом, расположенным в середине массива и в зависимости от результата сравнения (больше или меньше) дальнейший поиск проводится в левой или правой половине массива.

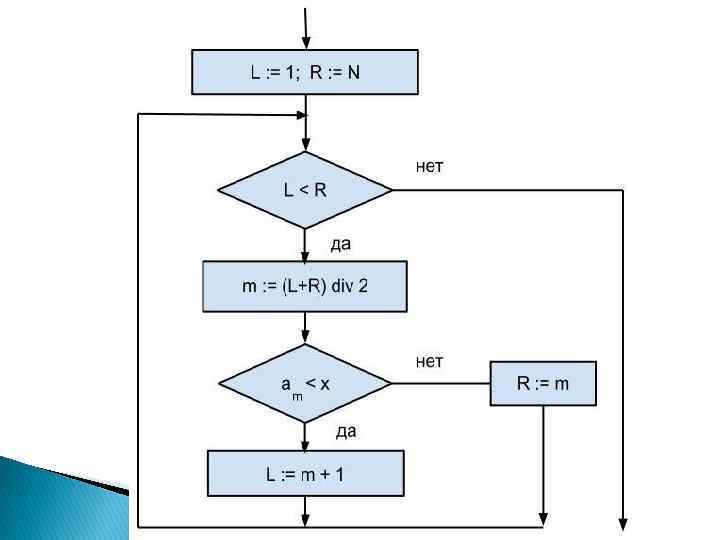
Пример: a 1, a 2, a 3, a 4, a 5, a 6, a 7, a 8, a 9 1, 3, 4, 7, 8, 9, 13, 20, 23 X=13 найти-? M = (L+R) div 2 – номер среднего элемента (div) если am < x (LR) = от 6 до 9 = m (6+9) div 2 = 7 m=7

Сортировка с помощью прямого включения Элементы мысленно делятся на уже «готовую последовательность» и неправильно расположенную последовательность Теперь на каждом шаге, начиная с i = 2, из 2 неправильно расположенной последовательности извлекается очередной элемент и перекладывается в готовую последовательность на нужное место.

На каждом шаге правый элемент из числа неотсортированных включается на соответствующее ему место в отсортированной последовательности, сдвигая правую часть отсортированной последовательности на одно место вправо. a 4, a , a 1 , a 2 , a 3 , 5 отсортированный a 1 , a 2 , a 4, a 6 неотсортированный 3 a 5 , a 6 , a 7 - отсортированные сдвигаются вправо

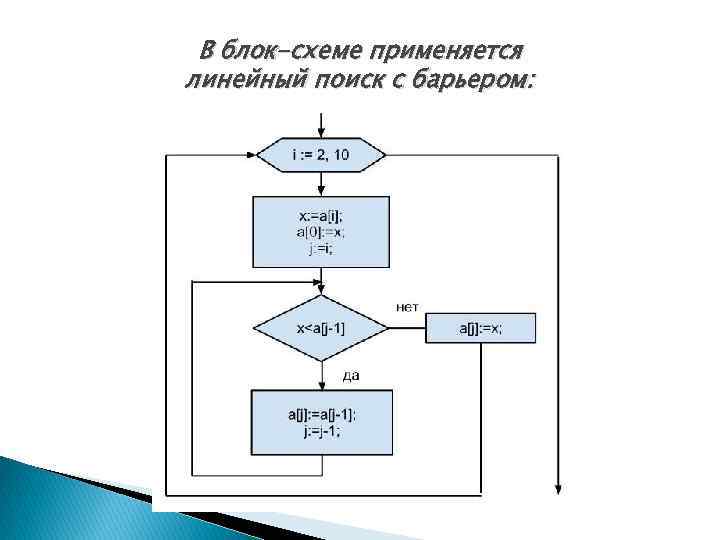В блок-схеме применяется линейный поиск с барьером:

Пример: 23, 34, 12, 13, 9 12, 23, 34, 13, 9 12, 13, 23, 34, 9 9, 12, 13, 23, 34

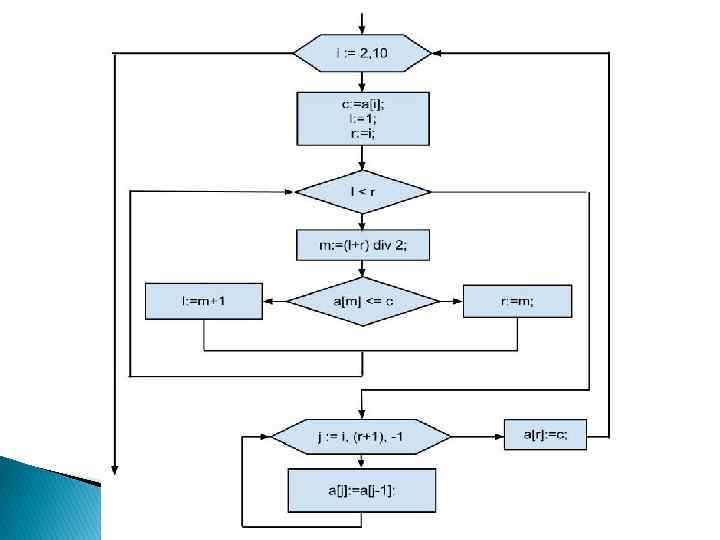
Сортировка с двойным включением определяется поиском деления пополам

Улучшенная сортировка включения (был предложен Д. Шеллом) Последовательность элементов делится на несколько групп, таким образом, что 2 элемента одной группы отстоят друг от друга на одинаковом расстоянии. Затем выполняется сортировка в каждой группе. После сортировки уменьшается количество групп и снова выполняется сортировка в группах. После этого эта операция выполняется до тех пор, пока не останется одна группа.

Пример: 44, 55, 12, 42, 94, 18, 6, 67 - расстояние 4 44, 18, 6, 42, 94, 55, 12, 67 – расстояние 2 6, 18, 12, 44, 55, 94, 67 – расстояние 1 6, 12, 18, 42, 44, 55, 67, 94

Сортировка с помощью прямого выбора На каждом этапе сортировки в неотсортированной части последовательности выполняется искомый элемент (наименьший) и помещается на первое место в этой неотсортированной части последовательности. Левая часть не трогается!

Пример: 1 2 3 4 5 12 15 17 11 13 i=2, min= 11 11 15 17 12 13 i=3. min=12 11 12 17 15 13 i=4, min=13 11 12 13 15 17 i=5, min=15