Алгоритмы обработки массивов Лекция Массив

Алгоритмы обработки массивов Лекция

Массив – структурированный тип данных, состоящий из фиксированного числа элементов одного типа, обозначенных одним именем Значение 12. 5 элемента Номер элемента в массиве 1 0. 48 -2. 4 2 3 43. 1 0 4 5 -17. 9 8. 0 6 7 248. 4 8

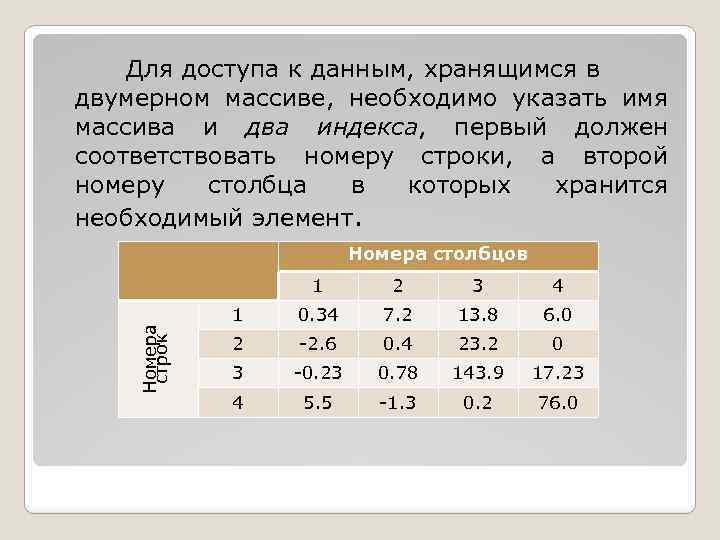
Для доступа к данным, хранящимся в двумерном массиве, необходимо указать имя массива и два индекса, первый должен соответствовать номеру строки, а второй номеру столбца в которых хранится необходимый элемент. Номера столбцов Номера строк 1 2 3 4 1 0. 34 7. 2 13. 8 6. 0 2 -2. 6 0. 4 23. 2 0 3 -0. 23 0. 78 143. 9 17. 23 4 5. 5 -1. 3 0. 2 76. 0

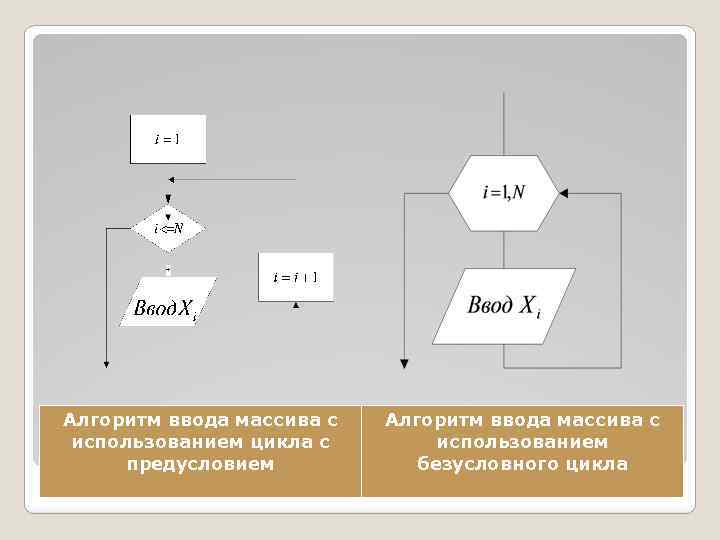
Алгоритм ввода массива с использованием цикла с предусловием Алгоритм ввода массива с использованием безусловного цикла

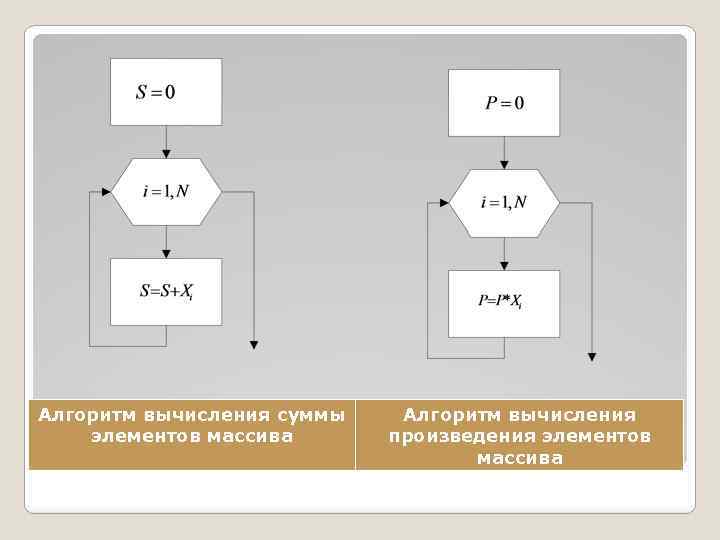
Алгоритм вычисления суммы элементов массива Алгоритм вычисления произведения элементов массива

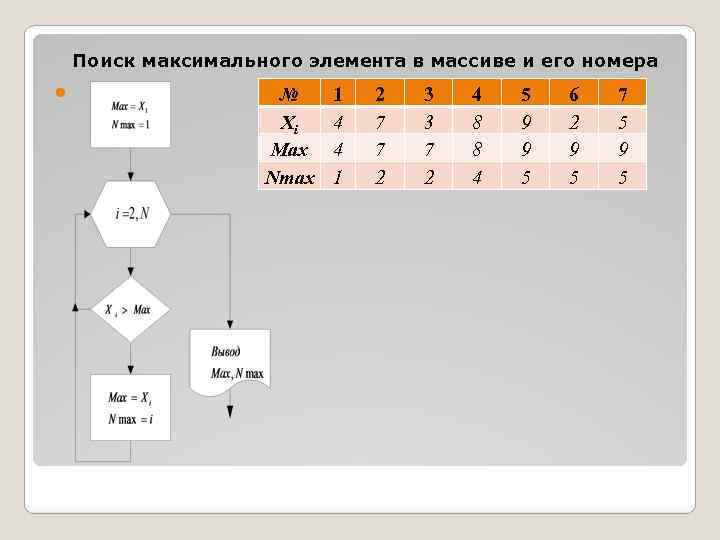
Поиск максимального элемента в массиве и его номера № Xi Max Nmax 1 4 4 1 2 7 7 2 3 3 7 2 4 8 8 4 5 9 9 5 6 2 9 5 7 5 9 5

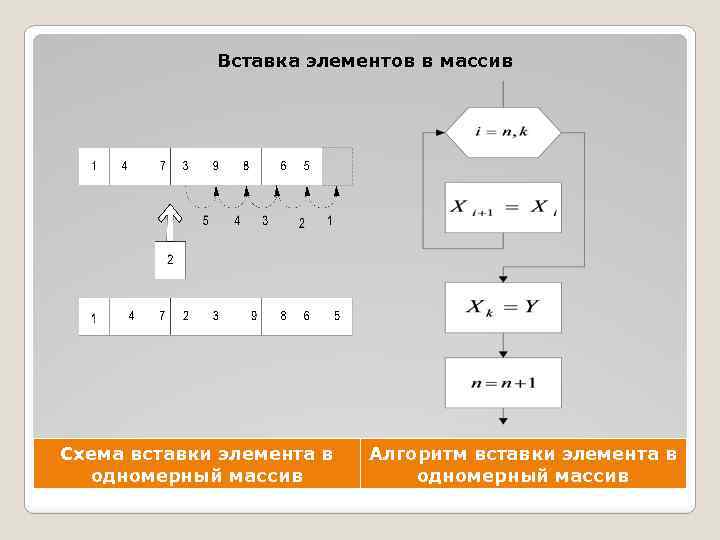
Вставка элементов в массив Схема вставки элемента в одномерный массив Алгоритм вставки элемента в одномерный массив

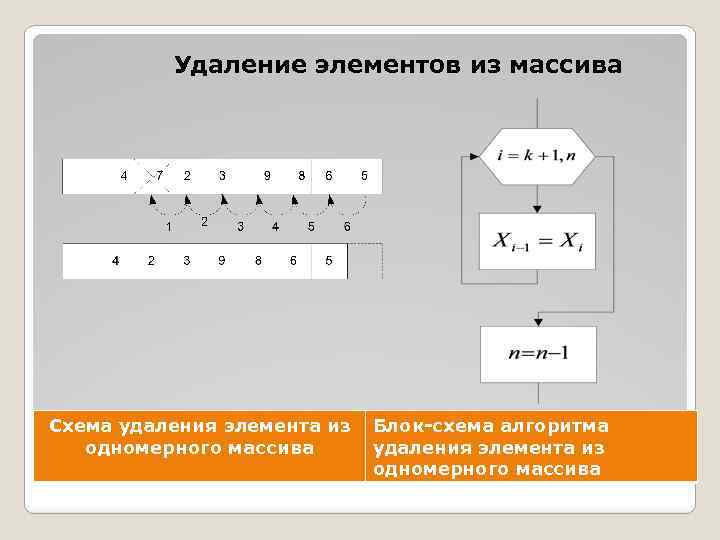
Удаление элементов из массива Схема удаления элемента из Блок-схема алгоритма одномерного массива удаления элемента из одномерного массива

Сортировка элементов в массиве Сортировка представляет собой процесс упорядочения элементов в массиве в порядке возрастания или убывания их значений. Например, массив X из n элементов будет отсортирован в порядке возрастания значений его элементов, если X 1≤X 2≤… ≤Xn, и в порядке убывания, если X 1≥X 2≥… ≥Xn. Существует большое количество алгоритмов сортировки, но все они базируются на трех основных: сортировка обменом; сортировка выбором; сортировка вставкой.

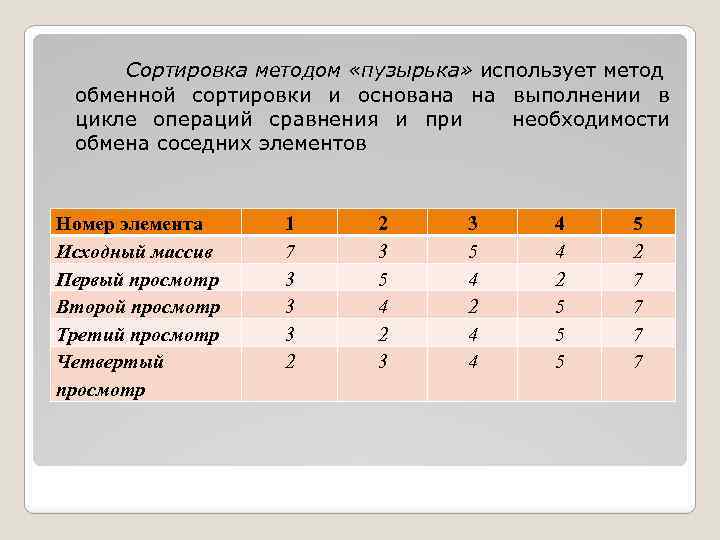
Сортировка методом «пузырька» использует метод обменной сортировки и основана на выполнении в цикле операций сравнения и при необходимости обмена соседних элементов Номер элемента Исходный массив Первый просмотр Второй просмотр Третий просмотр Четвертый просмотр 1 7 3 3 3 2 2 3 5 4 2 3 3 5 4 2 4 4 2 5 5 2 7 7

Блок-схема алгоритма сортировки массива методом «пузырька»

Сортировка выбором Алгоритм сортировки выбором основан на нахождении в массиве самого большого элемента и обмене его местами с последним. Далее, уменьшив количество просматриваемых элементов на единицу, меняем его местами с предпоследним элементом. Эту операцию поиска проводим до полного упорядочивания элементов в массиве

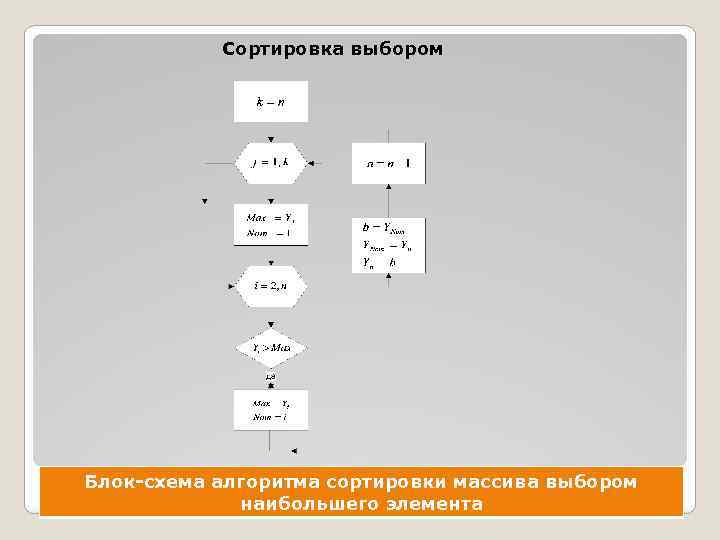
Сортировка выбором Блок-схема алгоритма сортировки массива выбором наибольшего элемента

Сортировка вставкой заключается в том, что сначала упорядочиваются два элемента массива. Затем делается вставка третьего элемента в соответствующее место по отношению к первым двум элементам. Четвертый элемент помещают в список из уже упорядоченных трех элементов. Этот процесс повторяется до тех пор, пока все элементы не будут упорядочены.

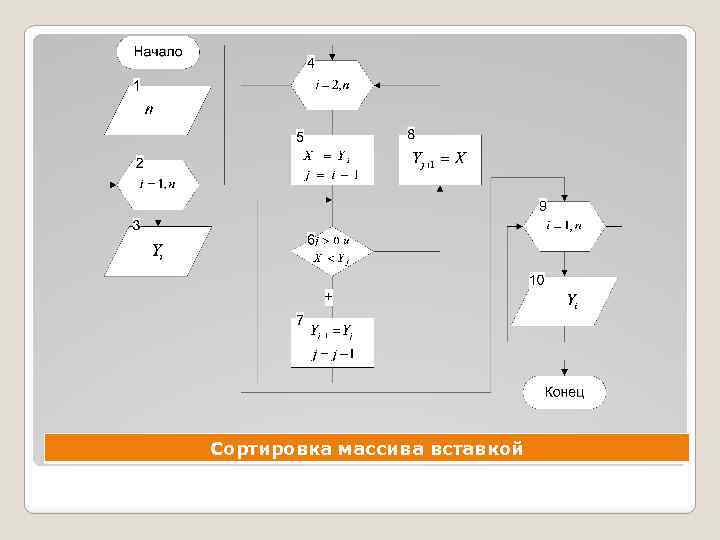
Сортировка массива вставкой

Примеры алгоритмов обработки массивов Дан массив А состоящий из k целых положительных чисел. Записать все четные по значению элементы массива А в массив В. i 1 2 3 4 5 6 7 8 А 3 7 4 9 2 8 1 6 В 4 2 8 6 m 1 2 3 4

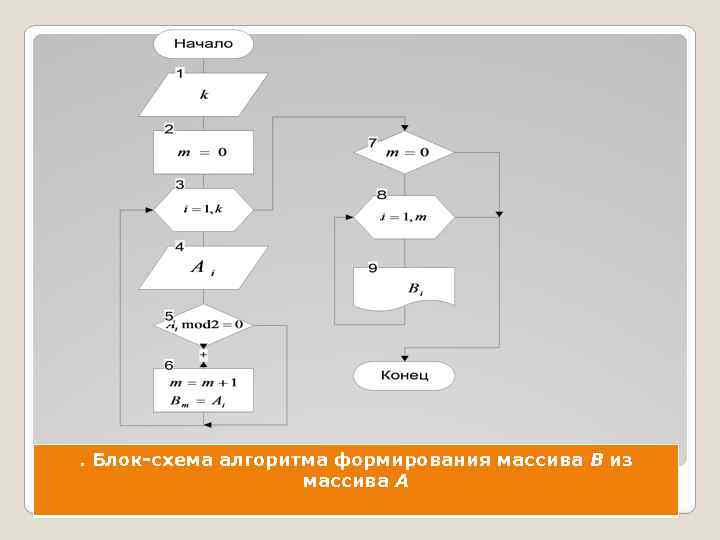
. Блок-схема алгоритма формирования массива В из массива А

Алгоритмы обработки матриц Матрица– это двумерный массив, каждый элемент которого имеет два индекса: номер строки – i; номер столбца – j. Поэтому для работы с элементами матрицы необходимо использовать два цикла. Если значениями параметра первого цикла будут номера строк матрицы, то значениями параметра второго – столбцы (или наоборот). Обработка матрицы заключается в том, что вначале поочередно рассматриваются элементы первой строки (столбца), затем второй и т. д. до последней.

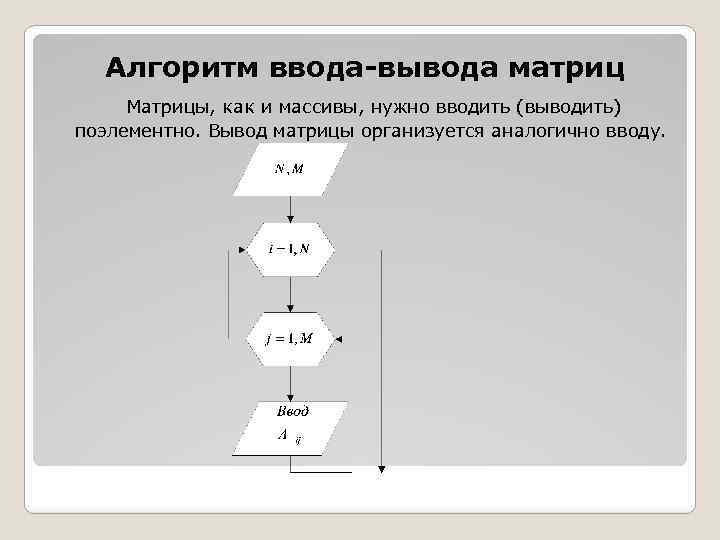
Алгоритм ввода-вывода матриц Матрицы, как и массивы, нужно вводить (выводить) поэлементно. Вывод матрицы организуется аналогично вводу.

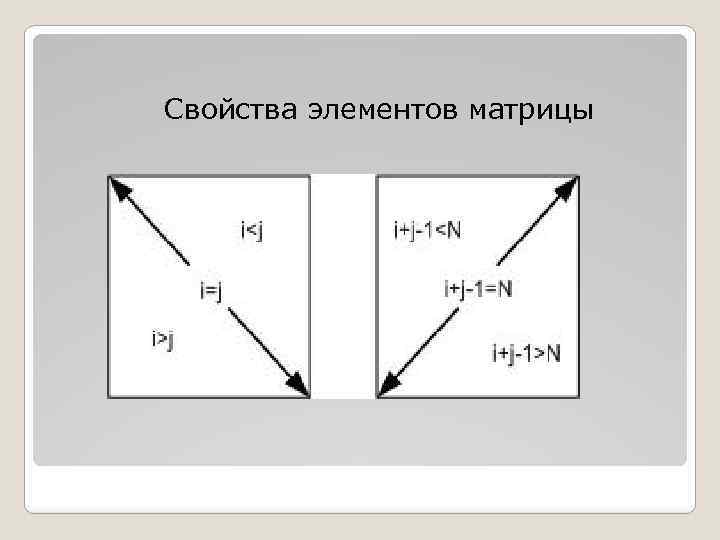
Свойства элементов матрицы

Свойства элементов матрицы если номер строки элемента совпадает с номером столбца (i=j), это означает что элемент лежит на главной диагонали матрицы; ·если номер строки превышает номер столбца (i>j), то элемент находится ниже главной диагонали; ·если номер столбца больше номера строки (i<j), то элемент находится выше главной диагонали. ·элемент лежит на побочной диагонали, если его индексы удовлетворяют равенству i+j– 1=n; ·неравенство i+j– 1<n характерно для элемента находящегося выше побочной диагонали; ·соответственно, элементу лежащему ниже побочной диагонали соответствует выражение i+j– 1>n.

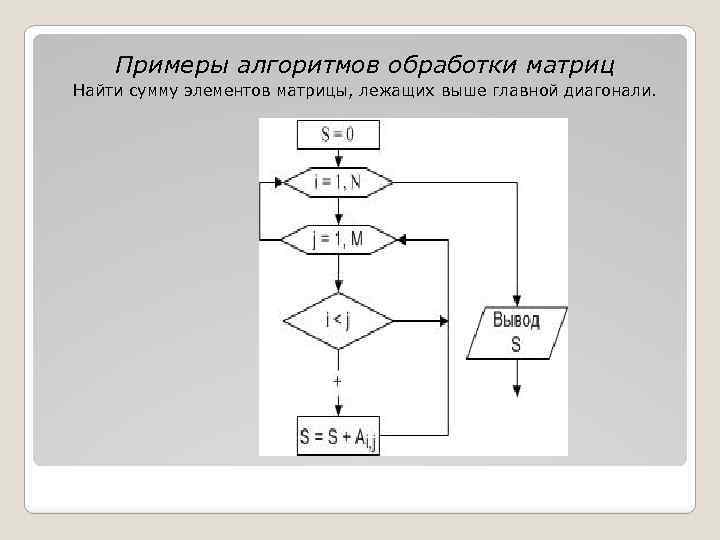
Примеры алгоритмов обработки матриц Найти сумму элементов матрицы, лежащих выше главной диагонали.

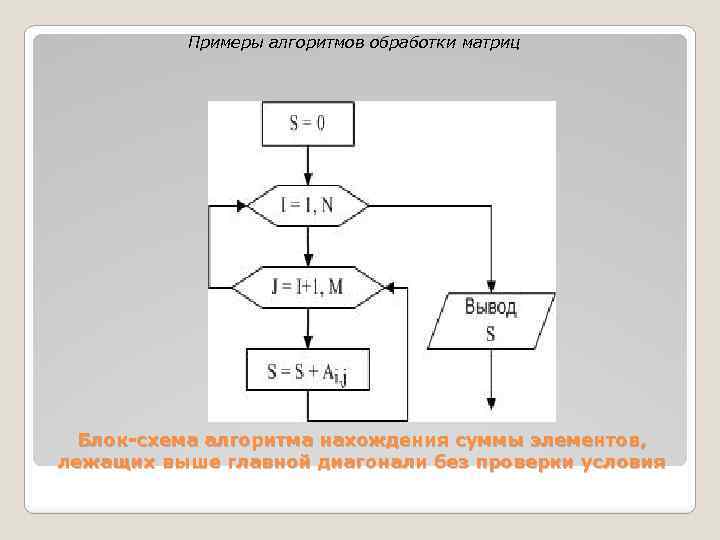
Примеры алгоритмов обработки матриц Блок-схема алгоритма нахождения суммы элементов, лежащих выше главной диагонали без проверки условия

Примеры алгоритмов обработки матриц Вычислить количество положительных элементов квадратной матрицы, расположенных по ее периметру и на диагоналях

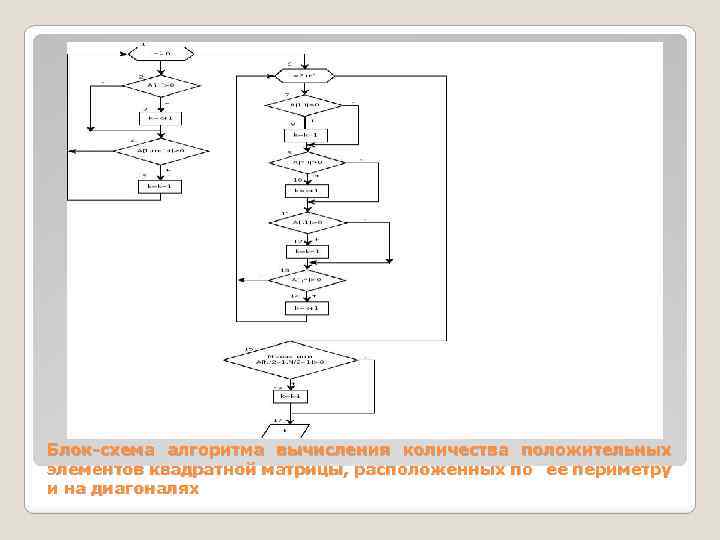
Блок-схема алгоритма вычисления количества положительных элементов квадратной матрицы, расположенных по ее периметру и на диагоналях

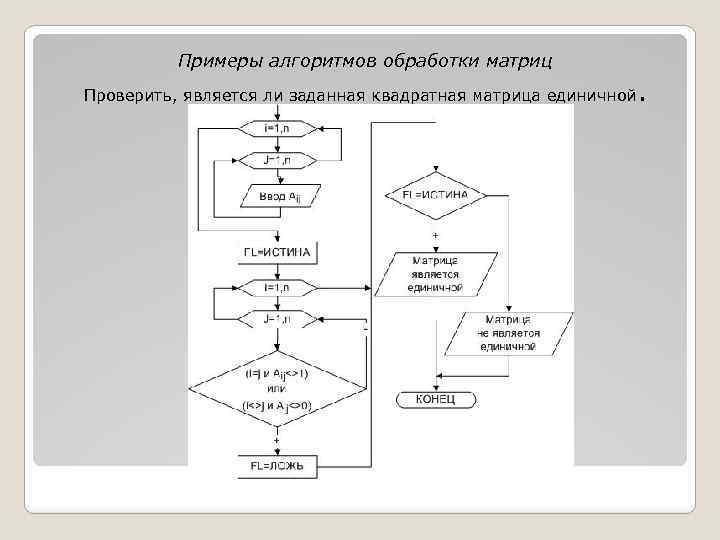
Примеры алгоритмов обработки матриц Проверить, является ли заданная квадратная матрица единичной .

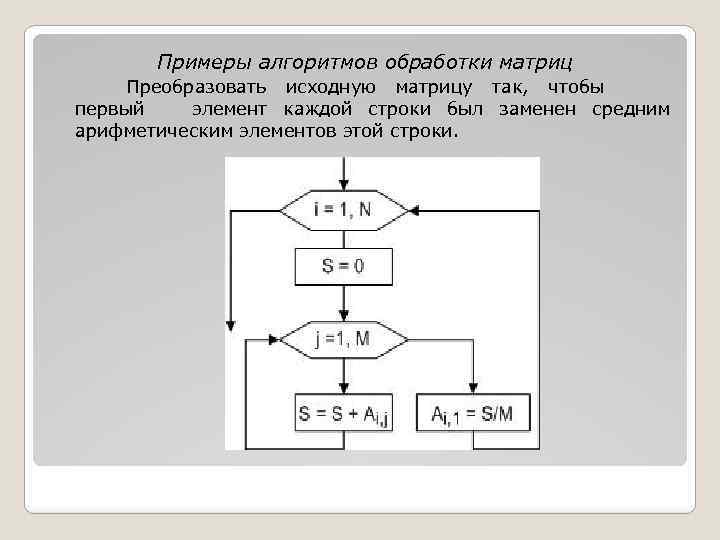
Примеры алгоритмов обработки матриц Преобразовать исходную матрицу так, чтобы первый элемент каждой строки был заменен средним арифметическим элементов этой строки.

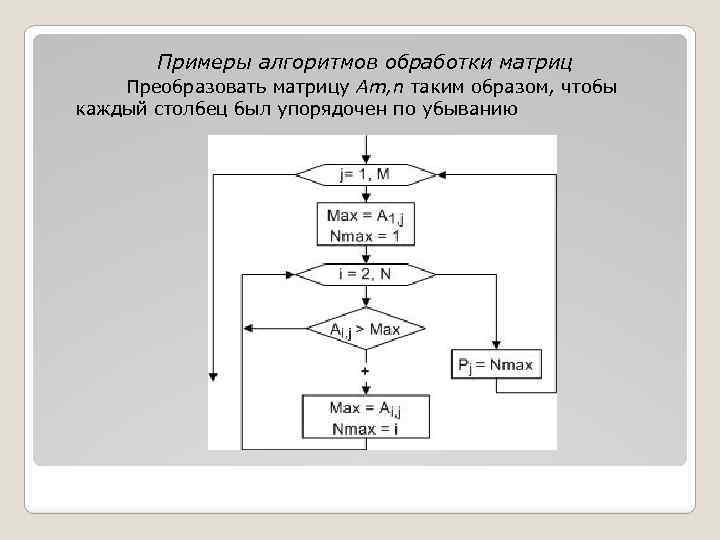
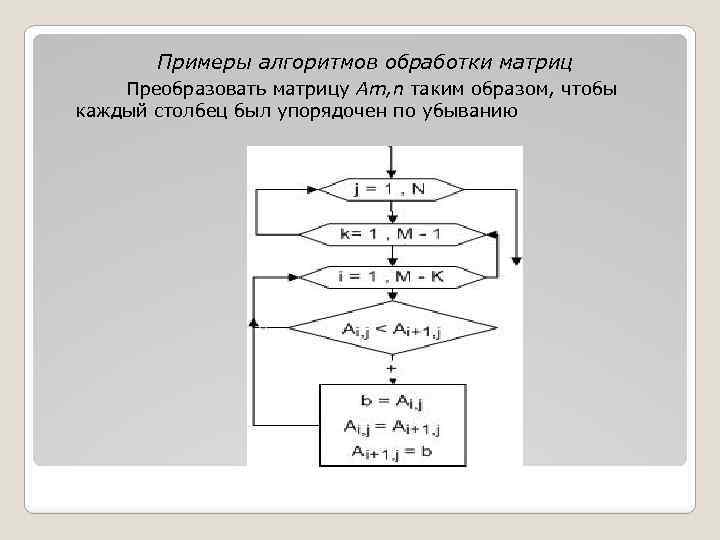
Примеры алгоритмов обработки матриц Преобразовать матрицу Am, n таким образом, чтобы каждый столбец был упорядочен по убыванию

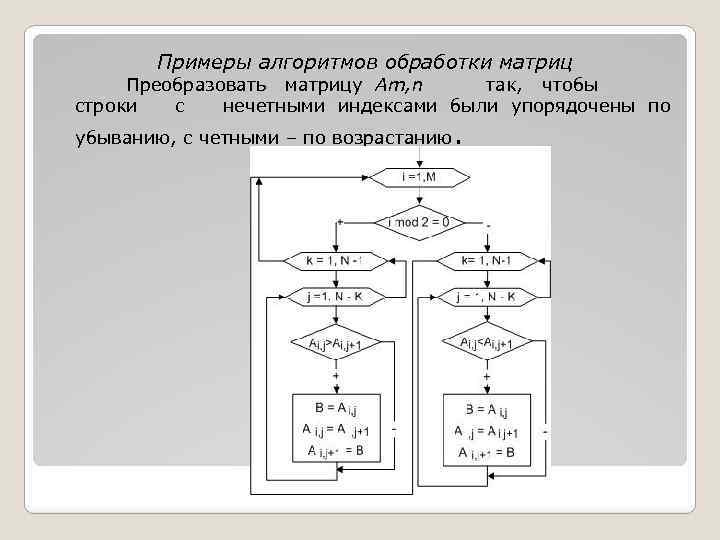
Примеры алгоритмов обработки матриц Преобразовать матрицу Am, n так, чтобы строки с нечетными индексами были упорядочены по убыванию, c четными – по возрастанию.