Алгоритмы на графах — 2 План лекции: Эйлеровы

Алгоритмы на графах - 2 План лекции: Эйлеровы циклы n Гамильтоновы циклы n Понятие NP-полной задачи n Методы перебора n Раскраска графа n Независимые и доминирующие множества вершин n Задача о максимальном потоке n Паросочетания в двудольных графах n автор: С. Н. Дроздов

Эйлеровы циклы n n Эйлеров цикл в неориентированном связном графе – такой цикл, который ровно по одному разу проходит через каждое ребро. Условие существования эйлерова цикла (необходимое и достаточное): все вершины связного графа должны быть четной степени. Эйлерова цепь: незамкнутый путь по всем ребрам между заданными вершинами. Условие существования эйлеровой цепи: начальная и конечная вершины имеют нечетную степень, остальные – четную. 2 Номера на ребрах – пример правильного порядка обхода. Пример неправильного начала обхода: 1 – 2 – 3 – 1 - ? ? ?

Алгоритм построения Эйлерова цикла n n Обходить вершины рекурсивно, удаляя пройденные ребра. При попадании в вершину, из которой нет ребер, выдавать ее как очередную вершину эйлерова пути и делать возврат из рекурсии. var A: array[1. . N, 1. . N] of 0. . 1; {Матрица смежности; будет испорчена!} Loop: array[1. . M] of Integer; {Порядок прохода ребер} k: Integer; {Число найденных ребер} procedure Search(v: Integer); for i : = 1 to N do if A[v, i] = 1 then begin A[v, i] : = 0; A[i, v] : = 0; Search[i]; end; k : = k + 1; Loop[k] : = v; end; . . . Трудоемкость: T(N, M) = O(N + M). k : = 0; Search(1); 3

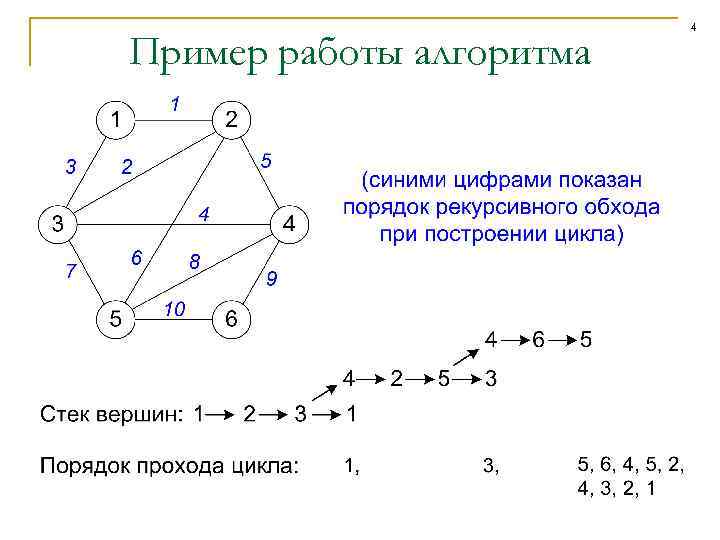Пример работы алгоритма 4

Гамильтоновы циклы n n Гамильтонов цикл в ориентированном или неориентированном связном графе – такой цикл, который ровно по одному разу проходит через каждую вершину. Задача поиска гамильтонова цикла – NPполная задача. Гамильтонова цепь: незамкнутый путь между заданными вершинами, проходящий через все остальные вершины (тоже NP-полная). Задача коммивояжера: заданы длины ребер и требуется найти кратчайший гамильтонов цикл. 5

Понятие NP-полной задачи n NP-полные задачи – обширный класс задач, для которых: q q q неизвестен (и вряд ли существует) хоть один алгоритм с полиномиальной оценкой трудоемкости (T(n) = O(nk) для какого-нибудь k); все известные алгоритмы предполагают более или менее полный перебор вариантов и имеют оценки экспоненциальные (O(an)) или хуже того (например, O(n!)); если когда-либо будет найден полиномиальный алгоритм для одной из NP-полных задач, то из него можно будет получить полиномиальные алгоритмы для всех остальных NP-полных задач. Но только не надо искать такой алгоритм в ходе соревнования!!! 6

Как поступать с NP-полными задачами n n Признаки NP-полноты олимпиадной задачи: щедрый лимит времени (несколько секунд) и жесткие ограничения размерности задачи (несколько десятков). На какую тему может быть такая задача: на любую. Чаще всего – графы, комбинаторика, составление расписаний, игры. Имеются простые универсальные методы организации перебора вариантов, легко приспосабливаемые к любой задаче. Однако специальные методы сокращения перебора, нацеленные на конкретную задачу, могут дать многократный выигрыш времени, поэтому думать полезно. 7

Рекурсивный перебор с возвратами n 8 Предполагаем, что решением задачи является некоторая допустимая (или оптимальная) комбинация значений переменных X 1, X 2, . . . , Xn. procedure Search(k: Integer); {k – количество уже выбранных значений X[1], X[2], . . . , X[k]} begin if (набор значений X[1], X[2], . . . , X[k] решает задачу)then Конец перебора; else begin k : = k + 1; for (все возможные значения X[k]) do if (набор значений X[1], X[2], . . . , X[k] допустимый) then Search(k); end; . . . Search(0); n Учет особенностей задачи часто позволяет сократить дерево перебора за счет отбрасывания бесперспективных значений X 1.

Последовательный перебор n Дополнительно предположим, что: q q n в любом допустимом решении число переменных n одно и то же; переменная Xk может принимать целочисленные значения от Lk до Hk. Тогда можно перебрать все комбинации примерно так, как перебираются цифры при инкрементировании десятичного числа (с переносом единицы в следующий разряд). for k : = 1 to N do X[k] : = L[k]; repeat Проверить комбинацию X[1], X[2], . . . , X[N]; k : = N; Carry : = True; while Carry and (k > 0) do begin X[k] : = X[k] + 1; Carry : = (X[k] > H[k]); if Carry then begin X[k] : = L[k]; k : = k – 1; end; until k = 0; 9

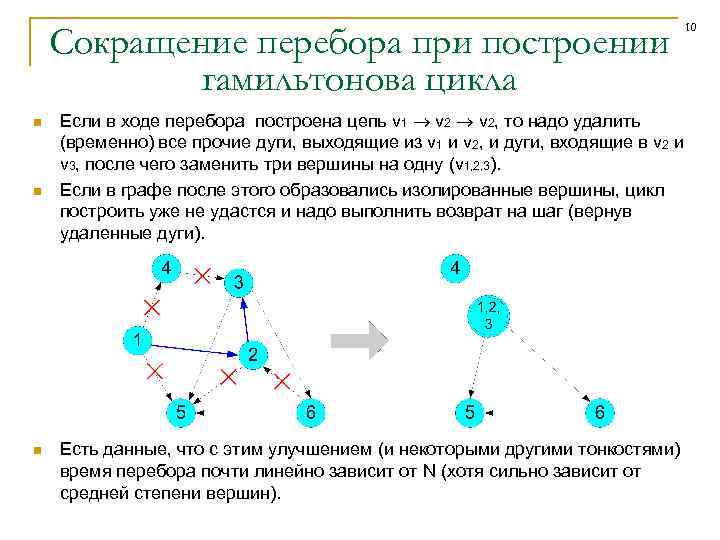Сокращение перебора при построении гамильтонова цикла n n n Если в ходе перебора построена цепь v 1 v 2, то надо удалить (временно) все прочие дуги, выходящие из v 1 и v 2, и дуги, входящие в v 2 и v 3, после чего заменить три вершины на одну (v 1, 2, 3). Если в графе после этого образовались изолированные вершины, цикл построить уже не удастся и надо выполнить возврат на шаг (вернув удаленные дуги). Есть данные, что с этим улучшением (и некоторыми другими тонкостями) время перебора почти линейно зависит от N (хотя сильно зависит от средней степени вершин). 10

Задача о раске графа n Дан неориентированный граф. Требуется сопоставить каждой вершине некоторое число (цвет), так, чтобы: q q n n никакие две смежные вершины не были одного цвета; число использованных цветов было бы минимальным. Минимально возможное число цветов называется хроматическим числом графа. Пределы возможных значений хроматического числа – от 1 (граф без ребер) до N (полный граф). Если граф планарный (т. е. его можно нарисовать так, чтобы ребра не пересекались), то всегда достаточно четырех цветов (это знаменитая «задача о четырех красках» ). Задача о раске – NP-полная. 11

Другие формулировки задачи о раске n n Раскрасить карту так, чтобы никакие две страны, имеющие общую границу, не были одного цвета. Пусть вершины – это некоторые объекты (люди, товары и т. п. ), а ребра показывают несовместимость объектов ( «этих двоих нельзя оставить в одной комнате» , «керосин нельзя хранить рядом с конфетами» и т. п. ). Требуется разделить объекты по группам (комнатам, контейнерам) с учетом совместимости. 12

Алгоритм неявного перебора для раски графа (алг. Кристофидеса) 13 Основная идея: сначала раскрасить вершины «жадным» способом, а затем пытаться улучшить раску, понемногу отказываясь от жадности. Для начала найти, на какой вершине k впервые потребовался максимальный цвет r, вернуться назад к вершине j, смежной с k, и попробовать покрасить ее цветом, на 1 большим – авось после этого удастся потом покрасить остальные, не используя цвет r. Далее чередовать приступы жадности с уступками, пока не потребуется перекрасить вершину j = 1. Это будет означать, что ничего улучшить уже нельзя. var k, j, k. New: Vertex; p, q, r, r. New: TColor; Color: array[1. . N] of TColor; n procedure Greedy. Color(start: Vertex; r. Max: TColor; var k. New: Vertex; r. New: TColor); {Начиная с вершины start, красит вершины в минимальные цвета. Завершается либо если требуется использовать цвет r. Max, либо когда докрасит все вершины. Возвращает максимальный использованный цвет r. New и номер вершины k. New, где этот цвет впервые потребовался. }

Алгоритм Кристофидеса (окончание) 14 function Prev. Adj(v: Vertex): Vertex; {Возвращает ближайший меньший, чем v, номер вершины, смежной с v}. . . Greedy. Color(1, , k, r); j : = Prev. Adj(k); {Попробуем немного отступить назад} if j > 1 then begin repeat p : = Color[j]; q : = min допустимый цвет для j, т. ч. q > p; {Мы не жадные} if q < r then begin Color[j] : = q; Greedy. Color(j+1, r, k. New, r. New); if r. New < r then begin {Отступление привело к победе!} r : = r - 1; k : = первая вершина цвета r; end else k : = k. New else k : = j; j : = Prev. Adj(k); {Опять отступаем назад} until j = 1; {Дальше отступать некуда} n ВНИМАНИЕ! Приведенный псевдокод в бою не проверен!

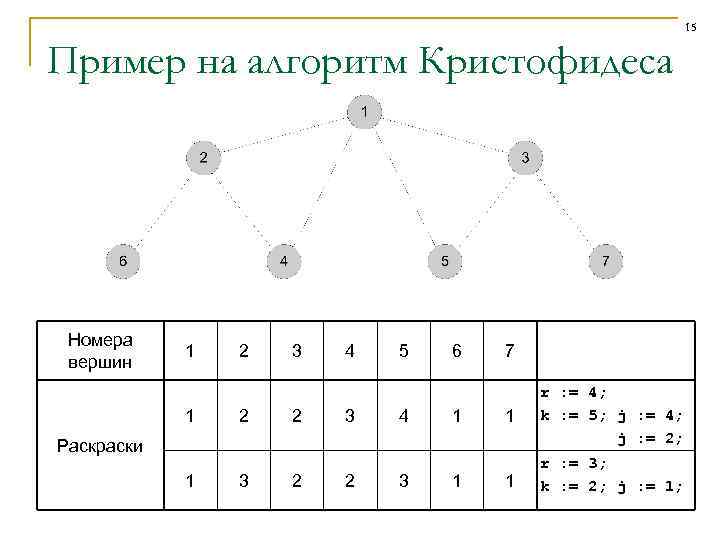15 Пример на алгоритм Кристофидеса Номера вершин 1 1 2 2 3 2 4 3 5 4 6 1 7 1 r : = 4; k : = 5; j : = 4; j : = 2; 1 r : = 3; k : = 2; j : = 1; Раскраски 1 3 2 2 3 1

Независимые множества вершин n n Дан неориентированный граф. Множество вершин называется независимым, если оно не содержит смежных вершин. Независимое множество называется максимальным, если в него нельзя добавить еще одну вершину. Не путать максимальное независимое множество с наибольшим по числу вершин (которое, конечно, является одним из максимальных). Задача поиска наибольшего независимого множества NP-полная. 16

Доминирующие множества вершин n n Дан ориентированный (или неориентированный) граф. Множество вершин называется доминирующим, если в каждую из остальных вершин ведет дуга от одной из вершин этого множества. Доминирующее множество называется минимальным, если из него нельзя исключить никакую вершину. Не путать минимальное доминирующее множество с наименьшим по числу вершин (которое, конечно, является одним из минимальных). Задача поиска наименьшего доминирующего множества NP-полная. 17

18 n n n Задача о максимальномпропускные способности Дан ориентированный граф, и заданы потоке в сети ребер {qij}, qij > 0. Выделены две вершины: s – источник, t – сток. Потоком в сети называется набор чисел {xij}, удовлетворяющий уравнениям сохранения потока: Число v называется значением потока. Требуется найти поток с максимальным значением.

Понятие аугментальной (увеличивающей) цепи n Аугментальной цепью относительно заданного потока называется неориентированная цепь ребер от источника к стоку, на которой: q для дуг, направленных от s к t (прямые дуги) ij = qij - xij > 0; q для дуг, направленных от t к s (обратные дуги) ij = xij > 0; ij = n n 19 7 5 4 6 3 5 Пусть = min ij. Если поток по всем прямым дугам увеличить на , а по обратным дугам уменьшить на , то уравнения сохранения не нарушатся, а значение потока увеличится на . Если не существует аугментальной цепи относительно имеющегося потока, то этот поток максимален.

Алгоритм поиска аугментальной цепи (алгоритм распространения пометок) n n Основная идея: будем, идя от стока, отмечать, сколько единиц потока можно дополнительно протолкнуть в следующие вершины (исходя из того, что есть в предыдущей вершине, и неизрасходованной пропускной способности соответствующей дуге). Уменьшение встречного потока равносильно увеличению прямого. Если удалось довести ненулевую прибавку до стока, то это и есть аугментальная цепь. Будем помечать вершины парой чисел (d, v): d – сколько добавили (d > 0) либо сколько убавили (d < 0); v – из какой вершины добавили либо в какую вершину убавили. Введем три состояния вершин: «Непомеченная» , «Помеченная» , «Обработанная» . Изначально s помечена (+ , s), остальные не помечены. Цикл, пока есть помеченные вершины, но t не помечена: q q n 20 выбрать любую помеченную (но не обработанную) вершину k; все непомеченные вершины i т. ч. есть дуга (k, i), пометить: (min(dk, qki - xki), k); все непомеченные вершины j т. ч. есть дуга (j, k), пометить: (min(dk, xjk), k); отметить вершину k как обработанную. Если по окончании цикла t осталась непомеченной, то аугментальной цепи нет.

Алгоритм Форда-Фалкерсона для задачи о максимальном потоке n n Взять начальный допустимый поток (например, нулевой); repeat q q попытаться построить аугментальную цепь; если удалось, то внести изменения в поток, пройдя обратным ходом от t до s с учетом пометок; n until больше не удается построить цепь. n Трудоемкость оценить затруднительно (легко оценить трудоемкость построения одной цепи, но трудно сказать, сколько раз удастся построить цепь), однако принять считать, что алгоритм достаточно эффективный. 21

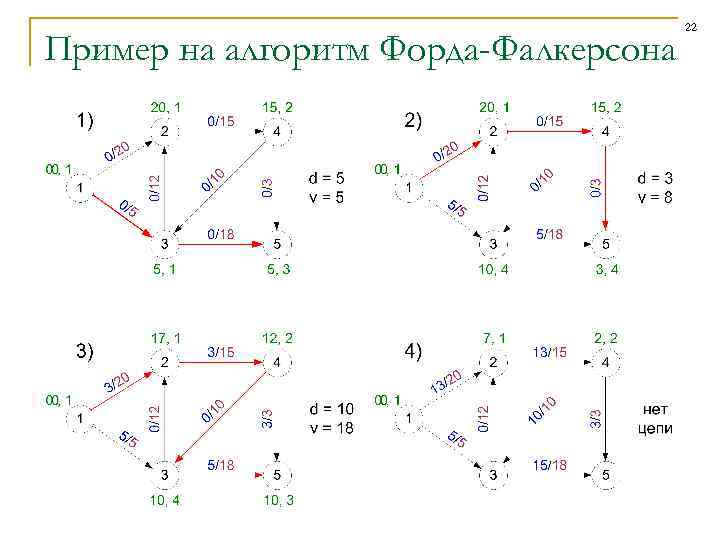Пример на алгоритм Форда-Фалкерсона 22

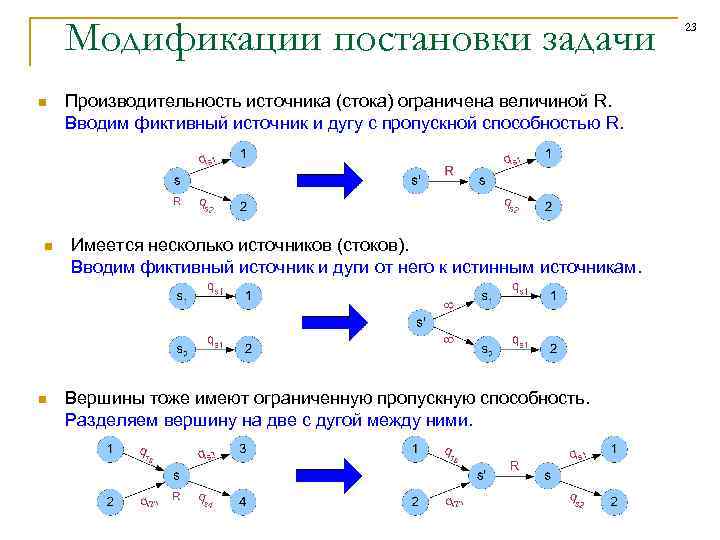Модификации постановки задачи n n n Производительность источника (стока) ограничена величиной R. Вводим фиктивный источник и дугу с пропускной способностью R. Имеется несколько источников (стоков). Вводим фиктивный источник и дуги от него к истинным источникам. Вершины тоже имеют ограниченную пропускную способность. Разделяем вершину на две с дугой между ними. 23

Задачи, связанные с потоками n n n Найти число различных путей из s в t, не имеющих общих дуг. Оно равно макс. потоку от s до t при условии, что все qij = 1. Найти число различных путей из s в t, не имеющих общих вершин. Оно равно макс. потоку от s до t при условии, что пропускные способности всех вершин = 1. Найти минимальный реберный разрез между s и t, т. е. минимальное множество ребер, после удаления которых t становится недостижимо из s. Мощность разреза равна числу путей без общих дуг. Аналогично – найти минимальный вершинный разрез. В более общем случае: при произвольных пропускных способностях минимальный по пропускной способности разрез равен по величине максимальному потоку. 24

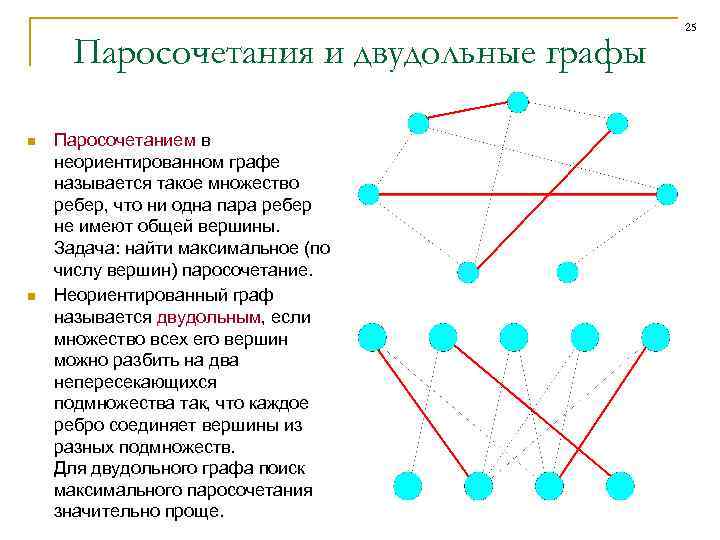Паросочетания и двудольные графы n n Паросочетанием в неориентированном графе называется такое множество ребер, что ни одна пара ребер не имеют общей вершины. Задача: найти максимальное (по числу вершин) паросочетание. Неориентированный граф называется двудольным, если множество всех его вершин можно разбить на два непересекающихся подмножества так, что каждое ребро соединяет вершины из разных подмножеств. Для двудольного графа поиск максимального паросочетания значительно проще. 25

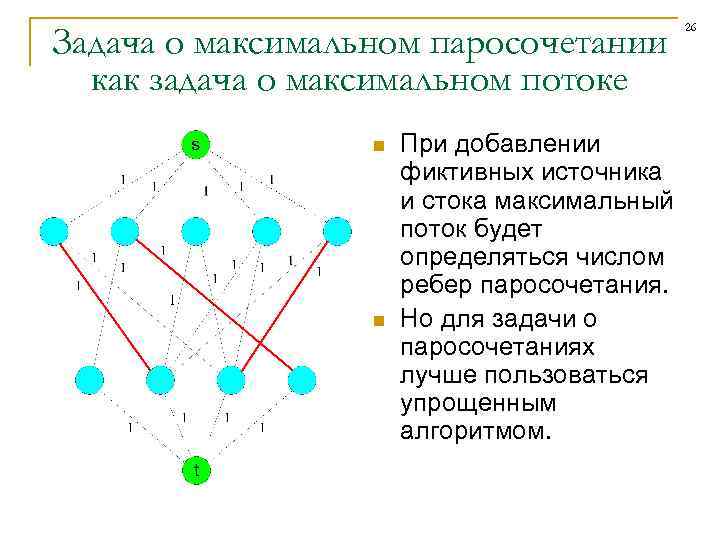Задача о максимальном паросочетании как задача о максимальном потоке n n При добавлении фиктивных источника и стока максимальный поток будет определяться числом ребер паросочетания. Но для задачи о паросочетаниях лучше пользоваться упрощенным алгоритмом. 26

Понятие чередующейся цепи n n Пусть в двудольном графе задано паросочетание P. Будем сокращенно называть «парными» / «непарными» вершины и ребра, принадлежащие / не принадлежащие P. Чередующейся цепью относительно P называется последовательность ребер, которая: q q n n 27 начинается с непарной вершины одного подмножества и заканчивается в непарной вершине другого подмножества; содержит чередование ребер: парное – непарное – (и т. д. ). Очевидно, что такая цепь содержит нечетное число ребер, причем начинается и заканчивается непарными ребрами. Если инвертировать состояние всех ребер цепи (непарные включить в P, а парные исключить), то P останется паросочетанием, но будет содержать на 1 ребро больше. Если невозможно построить чередующуюся цепь относительно P, то P – максимальное паросочетание. В терминах предыдущего слайда, чередующаяся цепь плюс еще два ребра (от источника и к стоку) образуют аугментальную цепь для потока.

Алгоритм построения чередующейся цепи 28 n n Основная идея: пытаться строить сразу все возможные цепи, исходя из всех непарных вершин одного из подмножеств (V 1). Цепь построена, если удалось по непарному ребру придти в непарную вершину другого подмножества. Начальный шаг: построить U 0 – множество непарных вершин V 1. Повторять для k : = 0, 1, … q Нечетный шаг: построить U 2 k+1 – множество вершин V 2, не включенных в предыдущие Ui и связанных непарным ребром с одной из вершин U 2 k. q Четный шаг: построить U 2 k+2 – множество вершин V 1, не включенных в предыдущие Ui и связанных парным ребром с одной из вершин U 2 k+1. Закончить цикл в одном из двух случаев: q q n На нечетном шаге найдена непарная вершина. Тем самым чередующаяся цепь построена. На очередном шаге получилось пустое множество вершин Ui. Построить чередующуюся цепь невозможно, данное паросочетание максимально. Построение чередующейся цепи повторяется, пока возможно.

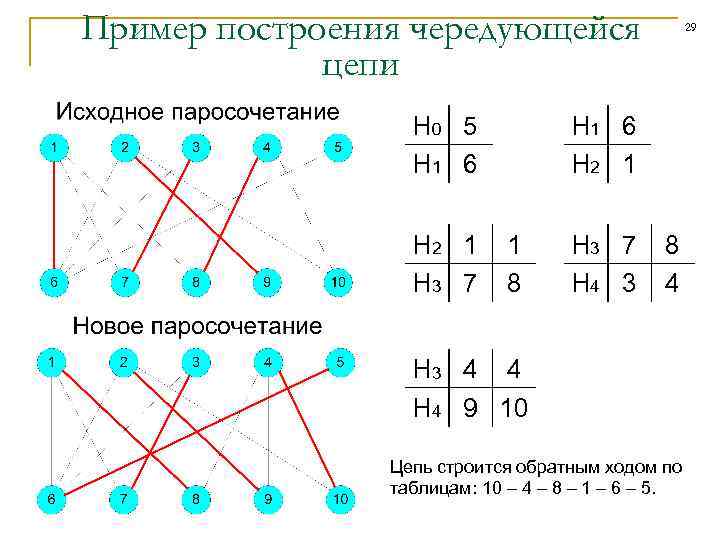Пример построения чередующейся цепи H 0 5 H 1 6 H 2 1 H 3 7 29 H 1 6 H 2 1 1 8 H 3 7 H 4 3 8 4 H 3 4 4 H 4 9 10 Цепь строится обратным ходом по таблицам: 10 – 4 – 8 – 1 – 6 – 5.