Алгоритмы и структуры данных Рекурсия 1 Способы

Алгоритмы и структуры данных. Рекурсия

1. Способы разработки алгоритмов. Два способа: • Применить подходящие структуры данных: – Списки, очереди, стеки. – Множества. – Графы, деревья. • Применить подходящий метод построения.

1. Способы разработки алгоритмов. Способы построения: • Рекурсия • Разделяй и властвуй. • Балансировка. • Динамическое программирование.

3. Рекурсия.

2. 1 Основные понятия Под индукцией понимается метод доказательства утверждений, который строится на базе индукции при n=0, 1, затем утверждение полагается правильным при некотором n и проводится доказательство для n+1.

2. 1 Основные понятия Рекурсивным называется объект частично состоящий или определяемый с помощью самого себя. Термин рекуррентные соотношения определяет математическое задание функции с помощью рекурсии. Если процедура р содержит явное обращение к самой себе, то она называется явно рекурсивной. Если процедура р содержит обращение к некоторой процедуре q, которая в свою очередь содержит прямое или косвенное обращение к р, то р - называется косвенно рекурсивной.

2. 1 Основные понятия 1. Натуральные числа f(0)=0 f(n)= f(n-1)+1 2. Факториал f(0)=1 f(n)= n*f(n-1) 3. Числа Фибоначчи f(0)=1 f(1)=1 f(n)= f(n-1)+ f(n-2), n>=2

2. 2 Примеры рекурсии Кривая Гильберта:

2. 2 Примеры рекурсии Кривая Гильберта: Hi+1 получается соединением 4 -х элементов Hi, повернутых и соединенных 3 -я линиями. Можно построить рекурсивный алгоритм

2. 2 Примеры рекурсии Кривая Гильберта: Где: A, B, C, В – 4 части, и стрелка показывает соединительную прямую

2. 2 Примеры рекурсии Кривая Гильберта H 5

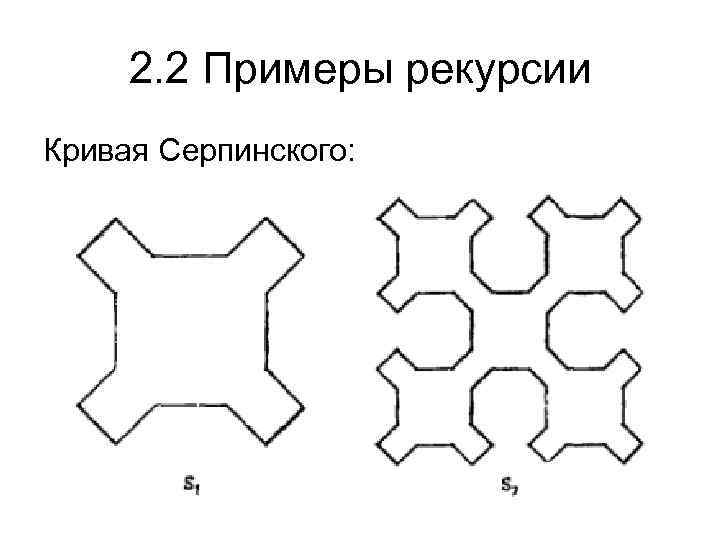
2. 2 Примеры рекурсии Кривая Серпинского:

2. 2 Примеры рекурсии Кривая Серпинского S 4

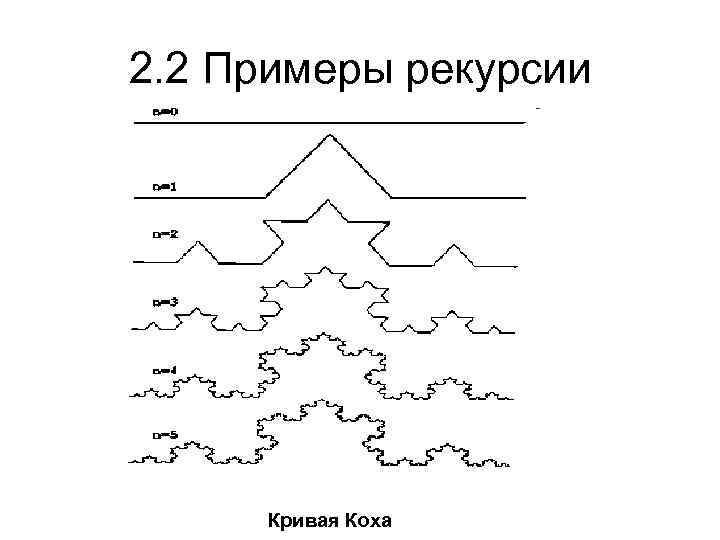
2. 2 Примеры рекурсии Кривая Коха

2. 2 Примеры рекурсии Построение "дракона" Хартера-Хейтуэя

2. 2 Примеры рекурсии

2. 3 Задание

2. 4. Недостатки рекурсии Рекурсивные алгоритмы подходят для задач, где данные определяются в терминах рекурсии. Следует избегать рекурсий там, где есть простое итеративно решение.

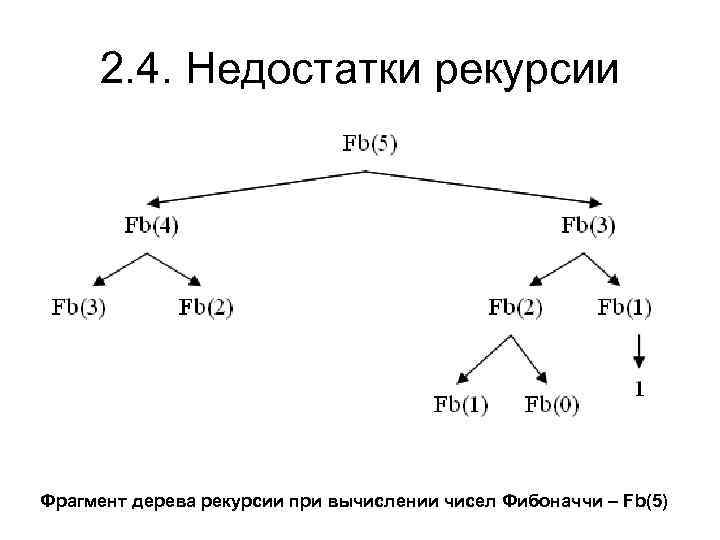
2. 4. Недостатки рекурсии Фрагмент дерева рекурсии при вычислении чисел Фибоначчи – Fb(5)

3. Алгоритмы с возвратом Алгоритмы, ищущие решение методом проб и ошибок. Процесс проб и ошибок разделяется на отдельные задачи по правилам рекурсии. В общем виде процесс – поиск строящий и обрезающий дерево подзадач.

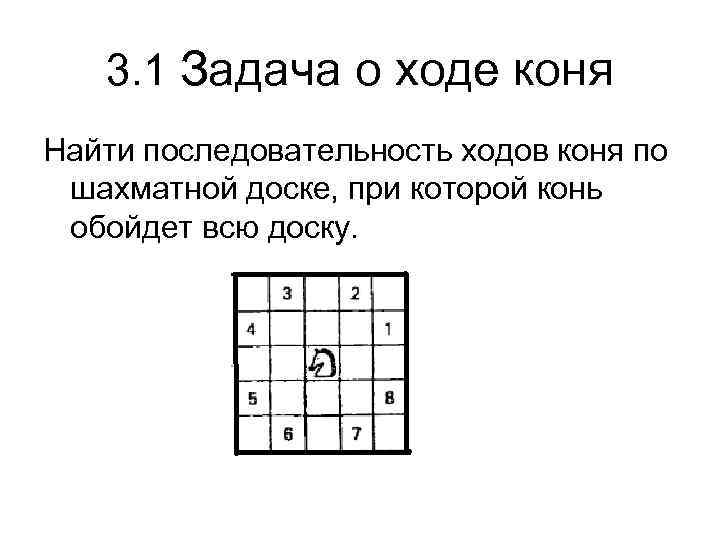
3. 1 Задача о ходе коня Найти последовательность ходов коня по шахматной доске, при которой конь обойдет всю доску.

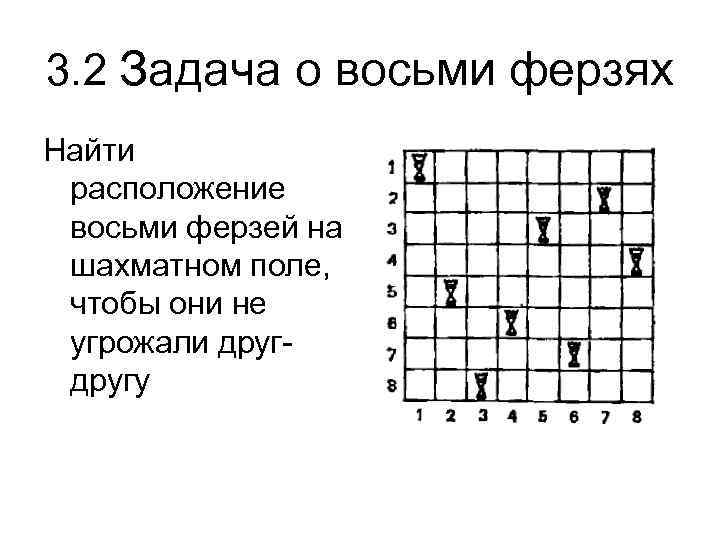
3. 2 Задача о восьми ферзях Найти расположение восьми ферзей на шахматном поле, чтобы они не угрожали другу

4. Разделяй и властвуй. Для решения задачу разбивают на более мелкие, и ищут решение каждой подзадачи, а затем получают решение всей задачи. Если применять рекурсию, то часто получаются эффективные алгоритмы.

4. 1 Умножение больших чисел. Пусть есть два больших n-разрядных числа x и y Тогда

4. 1 Умножение больших чисел. • Произведение можно вычислить так: • Требуется лишь 3 умножение n/2 разрядных числе. Несколько сложений и сдвигов.

4. 2 Умножение десятичных чисел.

4. 3. Балансировка Поддержание равновесия – основной принцип при разработке алгоритма.

4. 3. Балансировка Сортировка n целых чисел. Найти наименьший элемент, поставить его на первое место. Затем проделать ту же операцию для n-1, потом для n-2, n-3, …. , 2

4. 3. Балансировка Сортировка n целых чисел. Тогда

4. 3. Балансировка Сортировка n целых чисел. Сортировка слиянием Разбиваем множество на две, примерно равные части, проводим для каждой сортировку, потом эти множества сливаем.

4. 3. Балансировка Сортировка n целых чисел. Сортировка слиянием Тогда

5. 1 Динамическое программирование. • Динамическое программирование, как и метод разбиения, позволяет решать задачи, комбинируя решения вспомогательных задач. Динамическое программирование находит применение тогда, когда вспомогательные задачи не являются независимыми, т. е. когда разные вспомогательные задачи используют решения одних и тех же подзадач. • В алгоритме динамического программирования каждая вспомогательная задача решается только один раз, после чего ответ сохраняется в таблице. Это позволяет избежать одних и тех же повторных вычислений каждый раз, когда встречается данная подзадача. Динамическое программирование, как правило, применяется к задачам оптимизации.

5. 1 Динамическое программирование. Процесс разработки алгоритмов динамического программирования можно разбить на четыре этапа. 1. Описание структуры оптимального решения. 2. Рекурсивное определение значения, соответствующего оптимальному решению. 3. Вычисление значения, соответствующего оптимальному решению, с помощью метода восходящего анализа. 4. Составление оптимального решения на основе информации, полученной на предыдущих этапах.

5. 1 Динамическое программирование. • нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. • восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи.

5. 2. перемножение цепочки матриц Необходимо перемножить Порядок умножений определяется скобками

5. 2. перемножение цепочки матриц От порядка перемножений много зависит: Пример, есть три матрицы Различные варианты перемножений:

5. 2. перемножение цепочки матриц Постановка задачи: Для цепочки матриц Определить порядок матричного умножения, чтобы минимизировать количество операций.

5. 2. перемножение цепочки матриц • P(n) – количество вариантов расстановки скобок. • Можно показать, что

5. 2. перемножение цепочки матриц Решение: Если i<k<j, тогда Стоимость вычислений равна сумме стоимости вычисления матрицы и стоимости вычисления их произведения.

5. 2. перемножение цепочки матриц m[i, j] – минимальное количество вычислений для матрицы Pi - размер соответствующей матрицы

5. 2. перемножение цепочки матриц

5. 3. Элементы динамического программирования Для применения метода динамического программирования: • наличие оптимальной подструктуры • перекрывающиеся вспомогательные программы.

5. 3. Оптимальная подструктура Поиск оптимальной подструктуры происходит по общему образцу. 1. На первом этапе следует показать, что в процессе решения задачи приходится делать выбор. После выбора остается решить одну или несколько вспомогательных задач. 2. Предполагается, что найден выбор, ведущий к оптимальному решению. 3. Определяется, какие вспомогательные задачи получаются и как лучше охарактеризовать получающееся в результате пространство подзадач. 4. Показывается, что решения вспомогательных задач, возникающих в ходе оптимального решения задачи, сами должны быть оптимальными.

5. 3. Перекрытие вспомогательных задач Когда рекурсивный алгоритм снова и снова обращается к одной и той же задаче, говорят, что задача оптимизации содержит перекрывающиеся вспомогательные задачи. В алгоритмах динамического программирования обычно используется преимущество, заключающееся в наличии перекрывающихся вспомогательных задач. Это достигается путем однократного решения каждой вспомогательной задачи с последующим сохранением результатов в таблице, где при необходимости их можно будет найти за фиксированное время.

6. 1 Жадные алгоритмы В жадном алгоритме всегда делается выбор, который кажется самым лучшим в данный момент — т. е. производится локально оптимальный выбор в надежде, что он приведет к оптимальному решению глобальной задачи. Жадные алгоритмы не всегда приводят к оптимальному решению, но во многих задачах они дают нужный результат. Жадный метод обладает достаточной мощью и хорошо подходит для довольно широкого класса задач.

6. 1 Жадные алгоритмы Процесс разработки жадных алгоритмов: 1. Привести задачу оптимизации к виду, когда после сделанного выбора остается решить только одну подзадачу. 2. Доказать, что всегда существует такое оптимальное решение исходной задачи, которое можно получить путем жадного выбора, так что такой выбор всегда допустим. 3. Показать, что после жадного выбора остается подзадача, обладающая тем свойством, что объединение оптимального решения подзадачи со сделанным жадным выбором приводит к оптимальному решению исходной задачи.

6. 2. Нахождение кратчайшего пути