Алгоритмы и структуры данных Лекция 3 Массивы 1

Алгоритмы и структуры данных Лекция 3 Массивы 1

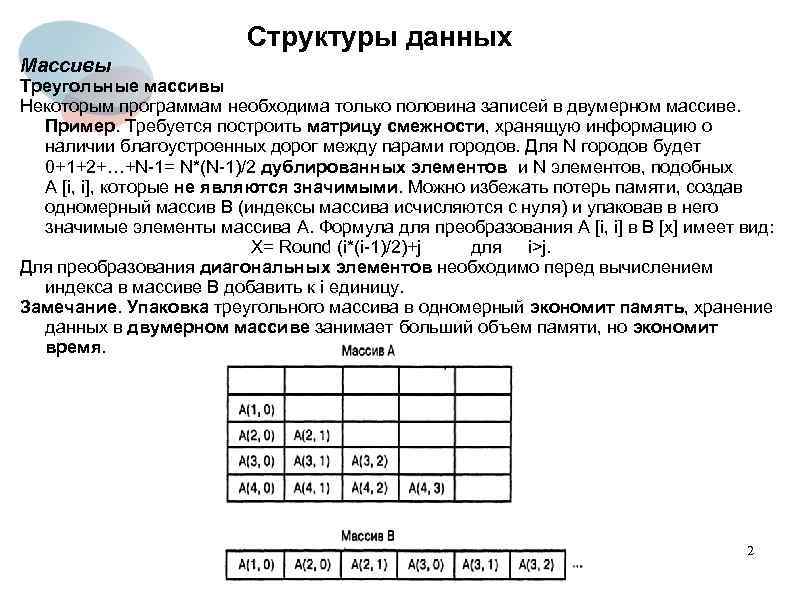Структуры данных Массивы Треугольные массивы Некоторым программам необходима только половина записей в двумерном массиве. Пример. Требуется построить матрицу смежности, хранящую информацию о наличии благоустроенных дорог между парами городов. Для N городов будет 0+1+2+…+N-1= N*(N-1)/2 дублированных элементов и N элементов, подобных A [i, i], которые не являются значимыми. Можно избежать потерь памяти, создав одномерный массив B (индексы массива исчисляются с нуля) и упаковав в него значимые элементы массива A. Формула для преобразования A [i, i] в B [x] имеет вид: Х= Round (i*(i-1)/2)+j для i>j. Для преобразования диагональных элементов необходимо перед вычислением индекса в массиве B добавить к i единицу. Замечание. Упаковка треугольного массива в одномерный экономит память, хранение данных в двумерном массиве занимает больший объем памяти, но экономит время. 2

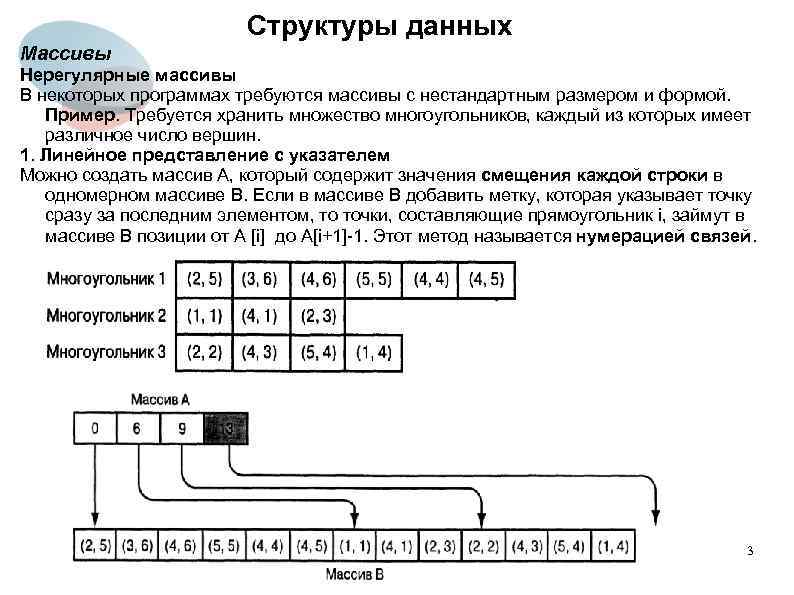Структуры данных Массивы Нерегулярные массивы В некоторых программах требуются массивы с нестандартным размером и формой. Пример. Требуется хранить множество многоугольников, каждый из которых имеет различное число вершин. 1. Линейное представление с указателем Можно создать массив A, который содержит значения смещения каждой строки в одномерном массиве B. Если в массиве B добавить метку, которая указывает точку сразу за последним элементом, то точки, составляющие прямоугольник i, займут в массиве B позиции от A [i] до A[i+1]-1. Этот метод называется нумерацией связей. 3

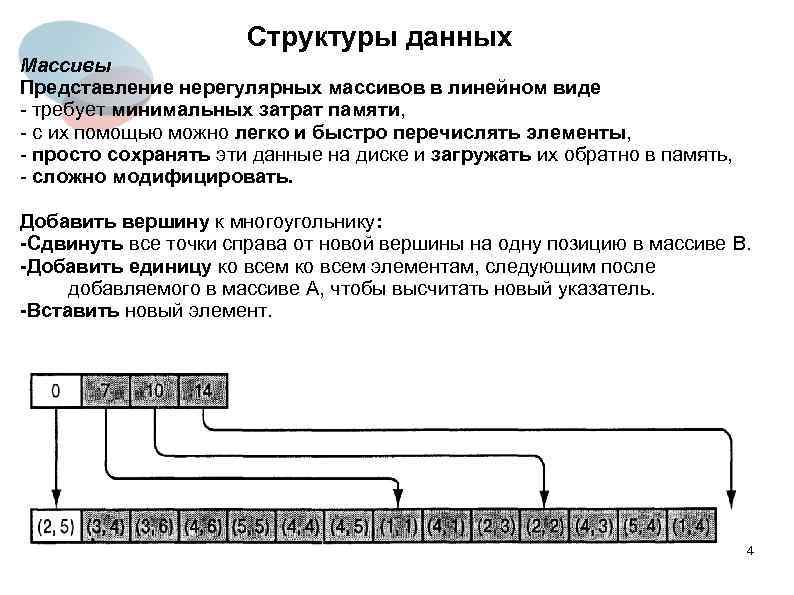Структуры данных Массивы Представление нерегулярных массивов в линейном виде - требует минимальных затрат памяти, - с их помощью можно легко и быстро перечислять элементы, - просто сохранять эти данные на диске и загружать их обратно в память, - сложно модифицировать. Добавить вершину к многоугольнику: -Сдвинуть все точки справа от новой вершины на одну позицию в массиве B. -Добавить единицу ко всем элементам, следующим после добавляемого в массиве A, чтобы высчитать новый указатель. -Вставить новый элемент. 4

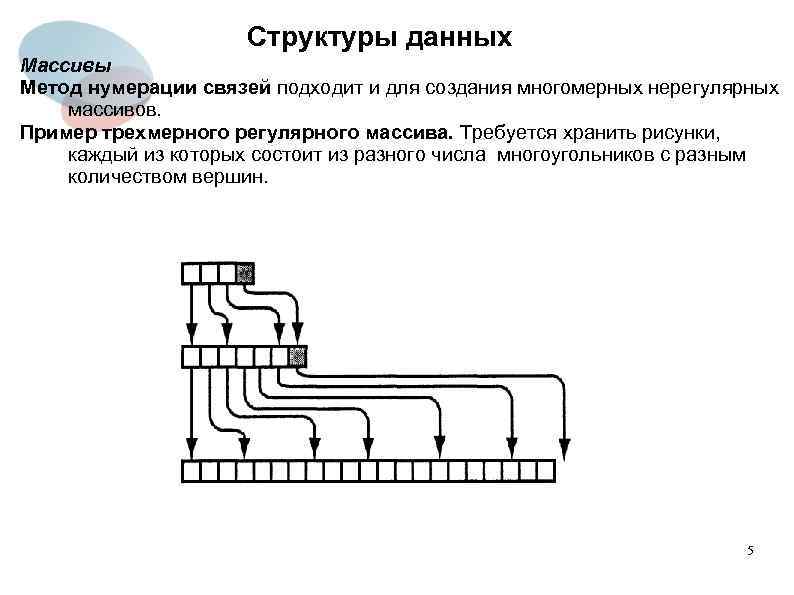Структуры данных Массивы Метод нумерации связей подходит и для создания многомерных нерегулярных массивов. Пример трехмерного регулярного массива. Требуется хранить рисунки, каждый из которых состоит из разного числа многоугольников с разным количеством вершин. 5

Структуры данных Массивы 2. Нерегулярные связанные списки При использовании связанных списков каждая ячейка содержит указатель на следующую на своем уровне иерархии и указатель на список ячеек, находящихся на более низком уровне иерархии. Пример. Ячейка многоугольника может содержать указатель на следующий многоугольник и указатель на ячейку , в которой определены координаты его первой вершины. С помощью этой методики можно без труда добавлять и удалять рисунки, многоугольники или точки в любом месте структуры. 6

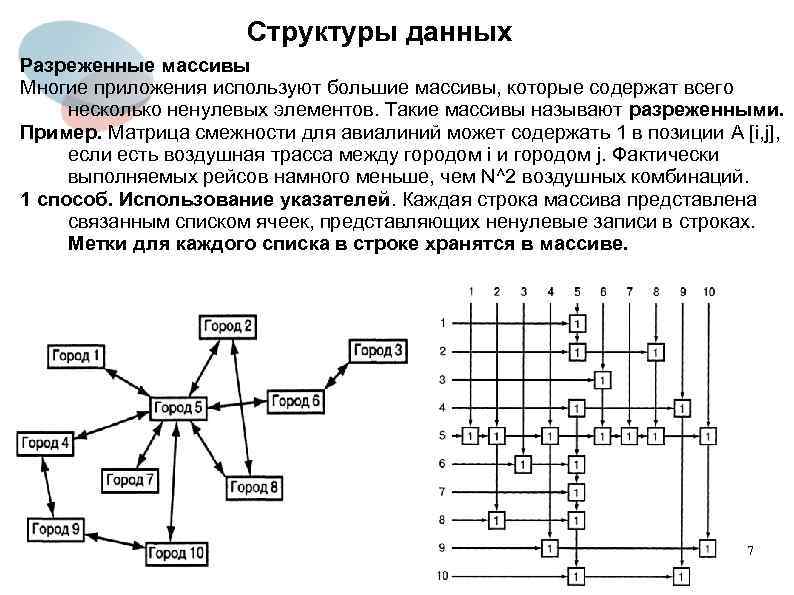Структуры данных Разреженные массивы Многие приложения используют большие массивы, которые содержат всего несколько ненулевых элементов. Такие массивы называют разреженными. Пример. Матрица смежности для авиалиний может содержать 1 в позиции A [i, j], если есть воздушная трасса между городом i и городом j. Фактически выполняемых рейсов намного меньше, чем N^2 воздушных комбинаций. 1 способ. Использование указателей. Каждая строка массива представлена связанным списком ячеек, представляющих ненулевые записи в строках. Метки для каждого списка в строке хранятся в массиве. 7

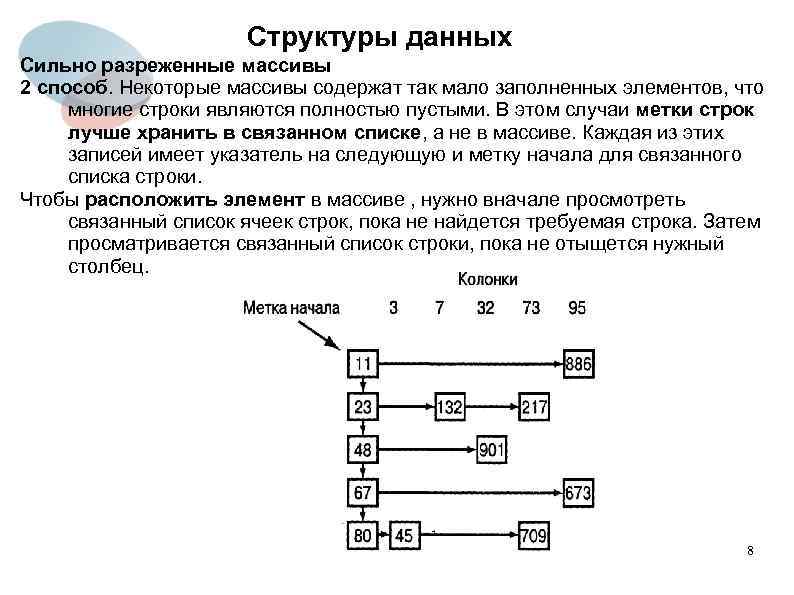Структуры данных Сильно разреженные массивы 2 способ. Некоторые массивы содержат так мало заполненных элементов, что многие строки являются полностью пустыми. В этом случаи метки строк лучше хранить в связанном списке, а не в массиве. Каждая из этих записей имеет указатель на следующую и метку начала для связанного списка строки. Чтобы расположить элемент в массиве , нужно вначале просмотреть связанный список ячеек строк, пока не найдется требуемая строка. Затем просматривается связанный список строки, пока не отыщется нужный столбец. 8

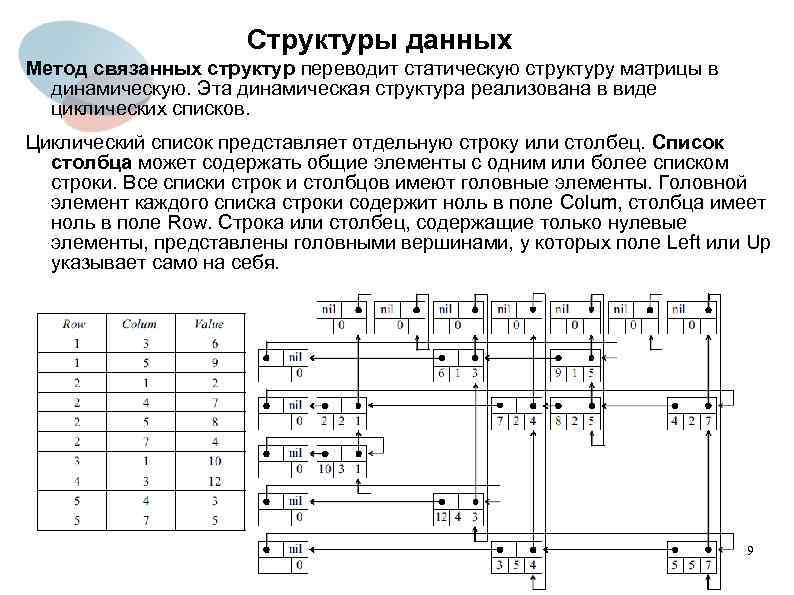Структуры данных Метод связанных структур переводит статическую структуру матрицы в динамическую. Эта динамическая структура реализована в виде циклических списков. Циклический список представляет отдельную строку или столбец. Список столбца может содержать общие элементы с одним или более списком строки. Все списки строк и столбцов имеют головные элементы. Головной элемент каждого списка строки содержит ноль в поле Colum, столбца имеет ноль в поле Row. Строка или столбец, содержащие только нулевые элементы, представлены головными вершинами, у которых поле Left или Up указывает само на себя. 9