Алгоритмы и структуры данных Алгоритмы поиска 1

Алгоритмы и структуры данных. Алгоритмы поиска

1. Постановка задачи • Данные делятся на записи, и каждая запись имеет хотя бы один ключ. Ключ используется для того, чтобы отличить одну запись от другой. • Целью поиска является нахождение всех записей подходящих к заданному ключу поиска. • Поиск - нахождение какой-либо конкретной информации в большом объеме ранее собранных данных.

2. Последовательный поиск Есть N – элементов, ищем ключ K. • • Установить i: =1 Если K=Ki алгоритм заканчивается i=i+1 Если i<=N, то перейти к шагу 2, иначе неуспешный поиск.

2. Последовательный поиск Время работы алгоритма: (5 C – 2 S + 3)u Где: • C – кол-во сравнений ключа • S = 1, если поиск успешен, 0 если неуспешен • u – единица времени

2. Последовательный поиск Модификация Есть N – элементов, ищем ключ K. • • Установить i: =1, Kn+1: =K Если K=Ki перейти к шагу 4 i=i+1, перейти к шагу 2 Если i<=N, алгоритм закончился успешно, иначе неуспешный поиск.

2. Последовательный поиск Время работы алгоритма: (4 C – 4 S + 10)u Где: • C – кол-во сравнений ключа • S = 1, если поиск успешен, 0 если неуспешен • u – единица времени

3. Двоичный поиск Поиск можно сделать значительно более эффективным, если данные будут упорядочены. Отсортировать список, потом выполнять поиск.

3. Двоичный поиск Простой алгоритм: 1. Установить l: = 1, u : = N. 2. [Получение средины. ] Если и < I, алгоритм завершается неудачно; иначе следует установить i : = [(l + u)/2, чтобы i соответствовало примерно середине рассматриваемой части таблицы. 3. [Сравнение. ] Если К < Кi, перейти к шагу 4; если К > Кi, перейти к шагу 5; если К = Ki, алгоритм успешно завершается. 4. [Изменение u. ] Установить u : = i — 1 и перейти к шагу 2. 5. [Изменение l. ] Установить l : = i + 1 и перейти к шагу 2.

3. Двоичный поиск Примеры двоичного поиска

4. Хеш-таблицы Раньше речь шла о поиске необходимой информации по заданному ключу путем прямого сравнения значения аргумента с искомым ключом. Общая идея подхода заключается в том, чтобы с помощью применения к заданному аргументу поиска x заранее определенной хэш-функции f(x) получить значение f(x), которое наилучшим образом характеризовало бы положение искомого ключа в основной или внешней памяти.

4. Хеш-таблицы Если количество реально хранящихся в массиве ключей мало по сравнению с количеством возможных значений ключей, эффективной альтернативой массива с прямой индексацией становится хеш-таблица, которая обычно использует массив с размером, пропорциональным количеству реально хранящихся в нем ключей. Вместо непосредственного использования ключа в качестве индекса массива, индекс вычисляется по значению ключа.

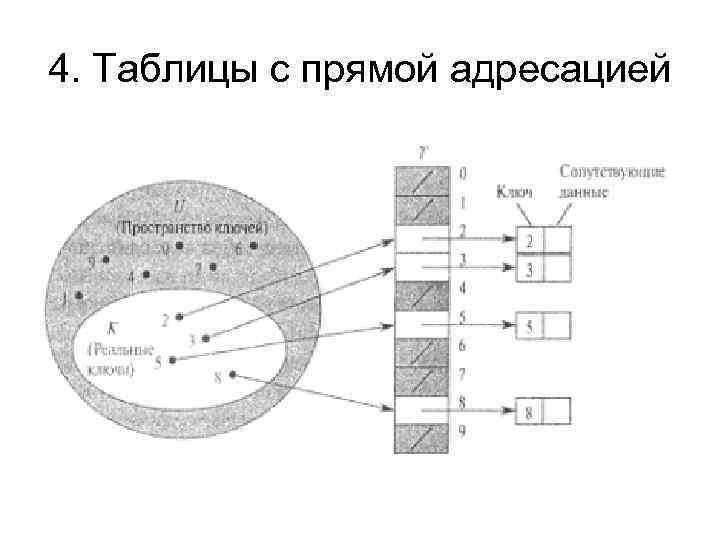4. Таблицы с прямой адресацией

4. Таблицы с прямой адресацией Недостаток прямой адресации очевиден: если пространство ключей U велико, хранение таблицы Т размером |U| непрактично. Кроме того, множество К реально сохраненных ключей может быть мало по сравнению с пространством ключей U, а в этом случае память, выделенная для таблицы Т, в основном расходуется напрасно.

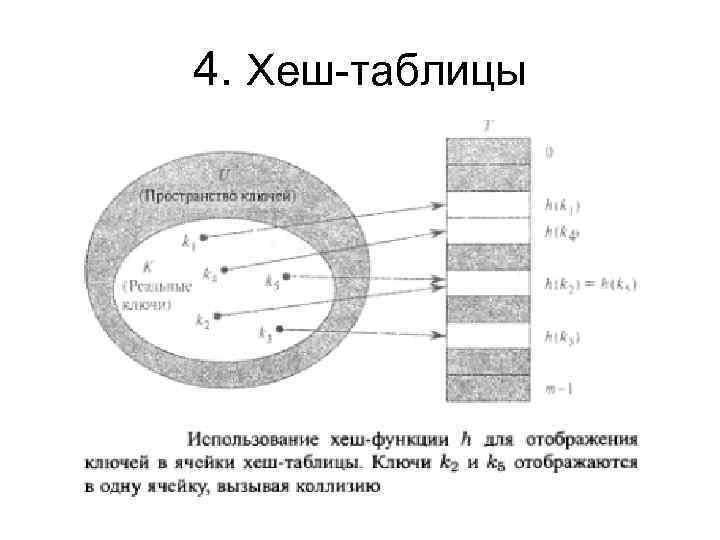4. Хеш-таблицы

4. Хеш-таблицы • Хеш-таблица требует существенно меньше места, чем таблица с прямой адресацией. • В случае прямой адресации элемент с ключом к хранится в ячейке к. При хешировании этот элемент хранится в ячейке h (к), т. е. мы используем хеш-функцию h для вычисления ячейки для данного ключа к. Функция h отображает пространство ключей U на ячейки хеш-таблицы Т [О. . m — 1]:

4. Хеш-таблицы Недостатки хеш-таблицы: • Два ключа хешируются в одну и туже ячейку. Ситуация – коллизия: • методом открытой адресации - (ключ, появление которого вызвало коллизию, помещается в один из свободных элементов хэш-таблицы) • методом цепочек - (записи, для ключей которых выработано одинаковое значение хэш-функции связываются в линейный список)

4. Хеш-таблицы Метод открытой адресации Если пытаемся поместить элемент в ячейку таблицы, а она занята то данная запись помещается в следующую свободную позицию в таблице. Недостатки метода. • Во-первых, он предполагает фиксированный размер таблицы. • Во -вторых, из такой таблицы трудно удалить запись.

4. Хеш-таблицы Метод цепочек - организацию связанного списка из всех записей, чьи ключи хешируются в одно и то же значение.

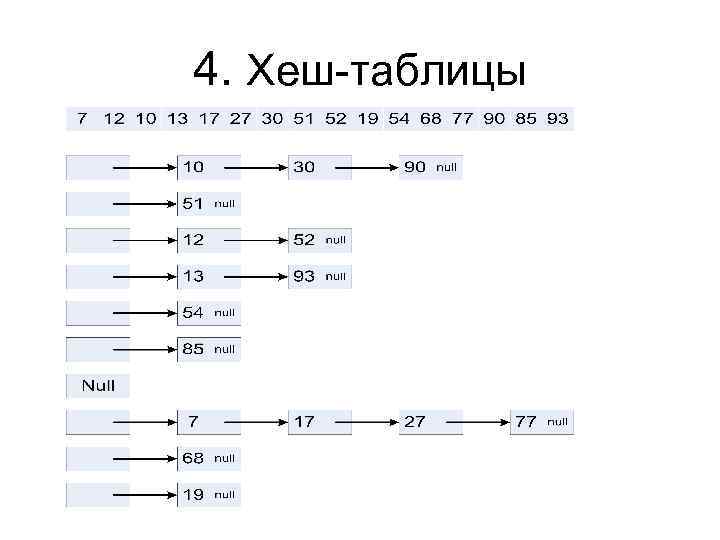4. Хеш-таблицы

4. Хеш-функции Как выбрать хорошую хеш-функцию? ■ Стойкость против попыток найти коллизии. ■ Обеспечивать невозможность вычислить исходные данные по результату преобразования. Нельзя определить, будет ли некоторая конкретная хеш-функция распределять ключи правильно, если эти ключи заранее не известны.

4. 1 Метод деления Некоторый целый ключ делится на размер таблицы и остаток от деления берется в качестве значения хешфункции. Эта хеш-функция обозначается h (key) : = key mod m.

4. 1 Метод середины квадрата Ключ умножается сам на себя и в качестве индекса используется несколько средних цифр этого квадрата.

4. 1 Хеш-функции Алгоритмы: • • • Adler-32 CRC SHA-1 SHA-2 (SHA-224, SHA-256, SHA-384, SHA-512) HAVAL MD 2 MD 4 MD 5 N-Hash RIPEMD-160 Snefru Tiger (TTH) Whirlpool ГОСТ Р 34. 11 -94 (ГОСТ 34. 311 -95)

4. 2 Применение Хэш-функций • • Проверка на наличие ошибок Проверка пароля Ускорение поиска данных Использование хеш-функций в криптографии

5. Поиск подстроки Одна из простейших задач поиска информации — поиск точно заданной подстроки в строке. Применение: • Поиск в тексте • Поиск в БД • ДНК

5. Поиск подстроки Алгоритмы? • «Враждебность» пользователя. • Архитектура процессора. • Грамматика языка. • Размер алфавита. • Возможность проиндексировать шаблон. • Требуется ли одновременный поиск нескольких строк?

5. 1 Простейший алгоритм поиска подстрок В простейшем алгоритме поиск всех допустимых сдвигов производится с по- помощью цикла, в котором проверяется условие Р[1. . га] = T[s + I. . S + т] для каждого из п — т + 1 возможных значений s. Naive_String_Matcher(T, Р) 1 n <- length[T] 2 m <— length[P] 3 for s <— 0 to n — m 4 do if P[1. . M] = T[s + 1. . s + m] 5 then print "Образец обнаружен при сдвиге" 5

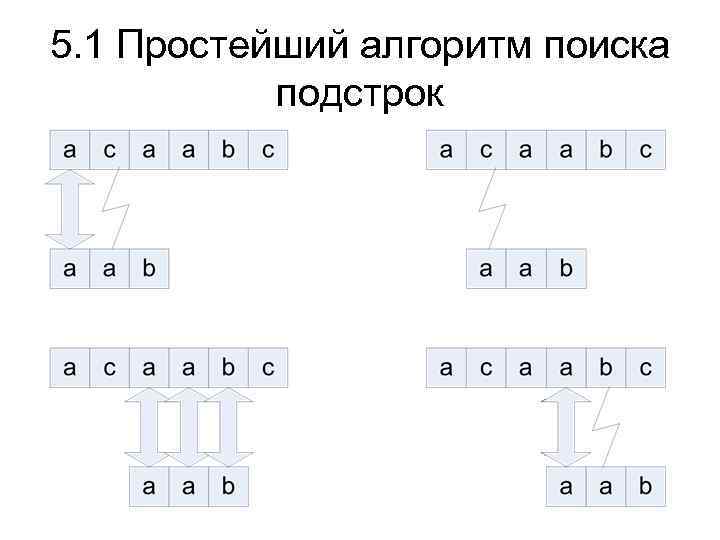5. 1 Простейший алгоритм поиска подстрок

5. 1 Простейший алгоритм поиска подстрок Время работы алгоритма O((n-m+1)m) Если m=n/2, то оценка O(n^2)

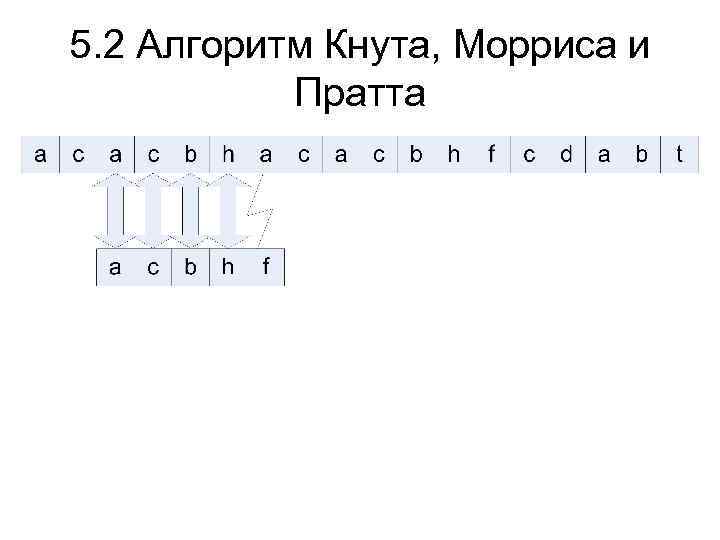
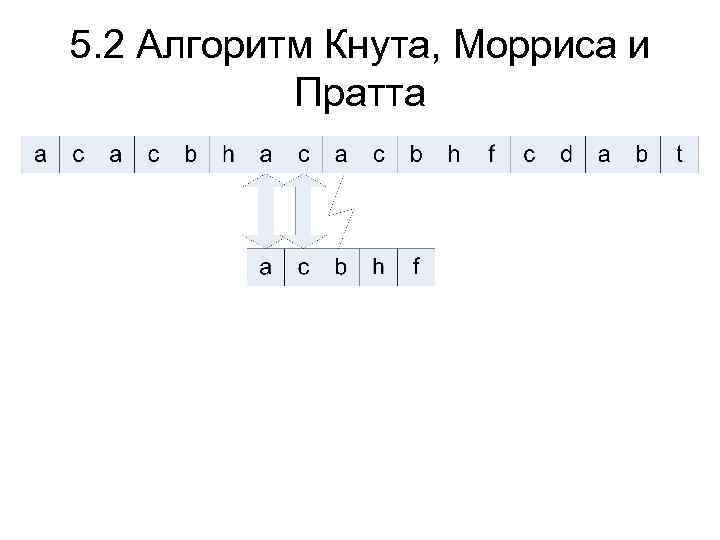
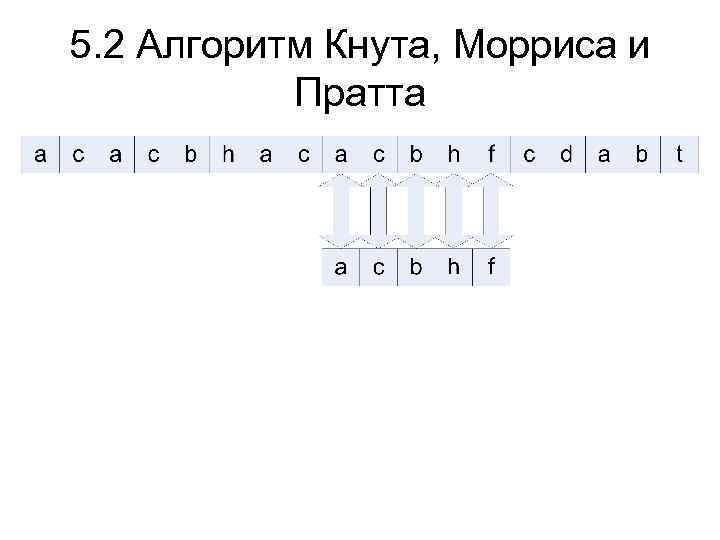
5. 2 Алгоритм Кнута, Морриса и Пратта Алгоритм основывается на том соображении, что, начиная каждый раз сравнение образа с самого начала, мы можем уничтожать ценную информацию. После частичного совпадения начальной части образа с соответствующими символами строки мы фактически знаем пройденную часть строки и можем «вычислить» некоторые сведения (на основе самого образа), с помощью которых потом быстро продвинемся по тексту.

5. 2 Алгоритм Кнута, Морриса и Пратта

5. 2 Алгоритм Кнута, Морриса и Пратта

5. 2 Алгоритм Кнута, Морриса и Пратта

5. 2 Алгоритм Кнута, Морриса и Пратта

5. 2 Алгоритм Кнута, Морриса и Пратта

5. 2 Алгоритм Кнута, Морриса и Пратта • Время работы алгоритма O(n+m)

5. 3 Алгоритм Боуэра и Мура Алгоритм Кнута, Морриса и Пратта дает выигрыш только когда происходят частичные совпадения. Алгоритм Боуэра и Мура основывается на необычном соображении— сравнение символов начинается с конца образа, а не с начала.

5. 3 Алгоритм Боуэра и Мура

5. 3 Алгоритм Боуэра и Мура

5. 3 Алгоритм Боуэра и Мура

5. 3 Алгоритм Боуэра и Мура

5. 3 Алгоритм Боуэра и Мура

5. 3 Алгоритм Боуэра и Мура Время сложности: Почти всегда требует меньше чем N сравнений, в некоторых случаях число сравнений N/M

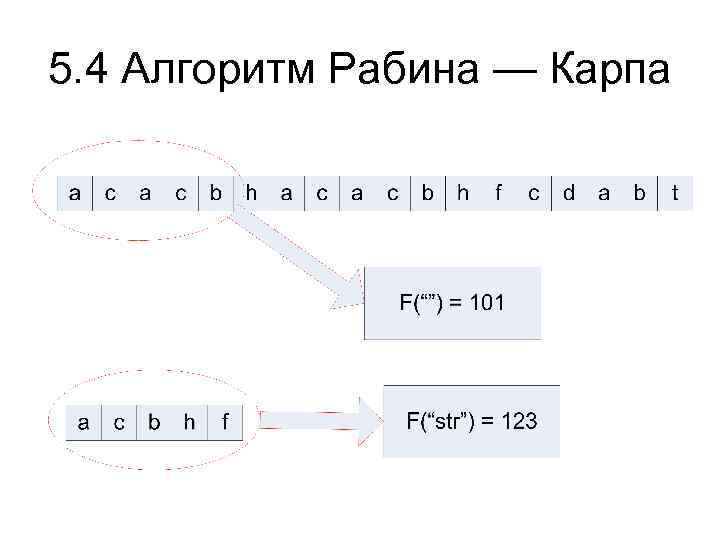
5. 4 Алгоритм Рабина — Карпа

5. 4 Алгоритм Рабина — Карпа

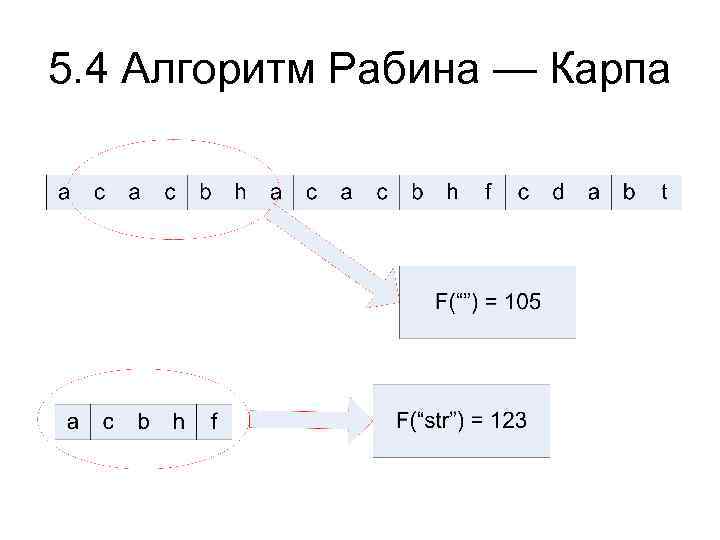5. 4 Алгоритм Рабина — Карпа

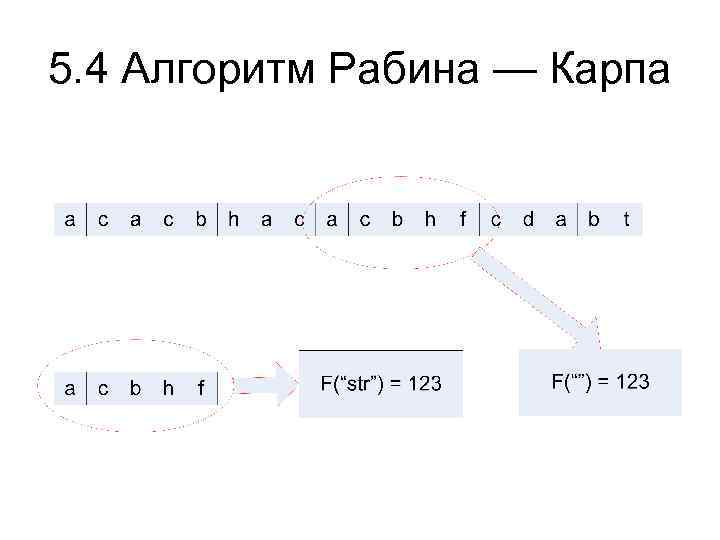5. 4 Алгоритм Рабина — Карпа