Алгоритмы анализ алгоритмов Лекция 1 Теория алгоритмов

Алгоритмы, анализ алгоритмов Лекция 1

Теория алгоритмов позволяют осуществить: • • рациональный выбор из известного множества алгоритмов решения данной задачи с учетом особенностей их применения (например, при ограничениях на размерность исходных данных или объема дополнительной памяти); получение временных оценок решения сложных задач;

Определение • • Алгоритм — набор инструкций, описывающих порядок действий исполнителя достижения результата решения задачи за конечное число действий. Алгоритм — это точно определённая инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи.

Свойства алгоритмов • • Дискретность — алгоритм должен представлять процесс решения задачи как последовательное выполнение некоторых простых шагов. При этом для выполнения каждого шага алгоритма требуется конечный отрезок времени, то есть преобразование исходных данных в результат осуществляется во времени дискретно. Детерминированность (определённость). В

Описание алгоритмов • Словесное описание • Блок-схема • Псевдокод • Flow-формы • Диаграммы Насси-Шнейдермана

Словесное описание • Click to edit the outline Это, по существу, • ПРИМЕР : Найти text format обычный язык, но с наибольшего из тщательным трёх заданных Second Outline Level отбором слов и чисел. Third Outline a, b, c. фраз, не Level допускающих Fourth Outline лишних слов, Level • 1. Сравнить a и b. двусмысленностей Fifth Если a>b, то в и повторений. качестве Outline Level Дополняется язык максимума t Sixth

Блок схемы • • • Правила выполнения схем определяются следующими документами: ГОСТ 19. 701 -90. Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения. ГОСТ 19. 003 -80. Схемы алгоритмов и программ. Обозначения условные графические.

Блок начала-конца алгоритма • Надпись на блоке: "начало" ("конец").

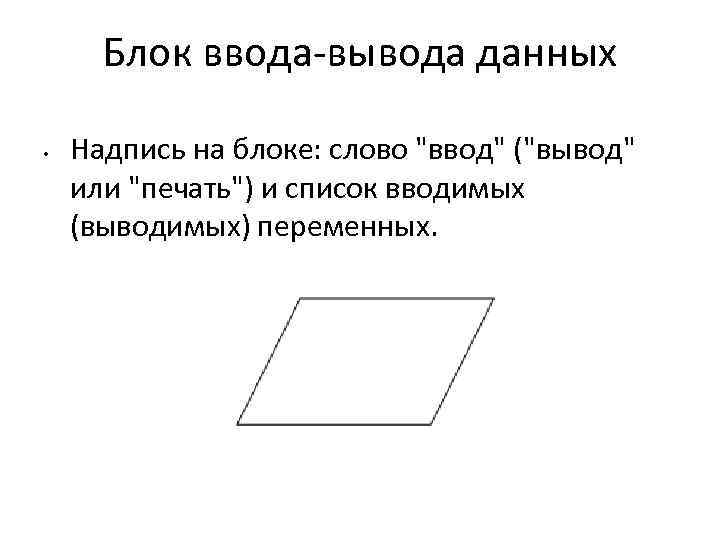Блок ввода-вывода данных • Надпись на блоке: слово "ввод" ("вывод" или "печать") и список вводимых (выводимых) переменных.

Блок операции • Элементарная (атомарная) операция по обработке данных (например, n=n+1)

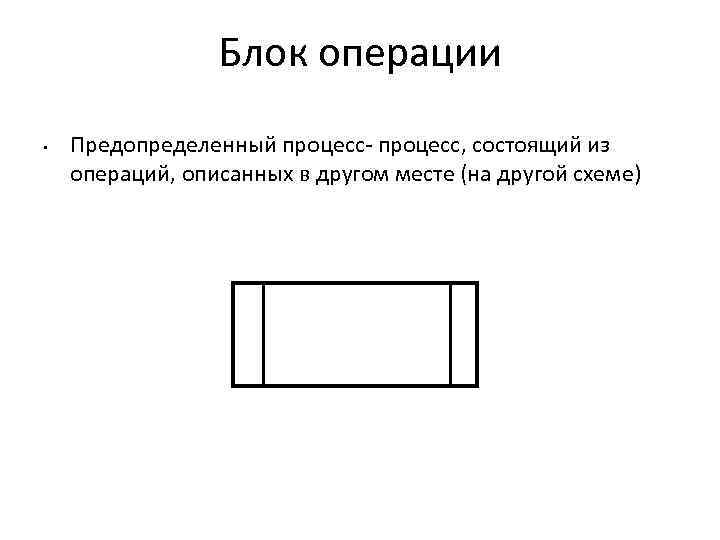Блок операции • Предопределенный процесс- процесс, состоящий из операций, описанных в другом месте (на другой схеме)

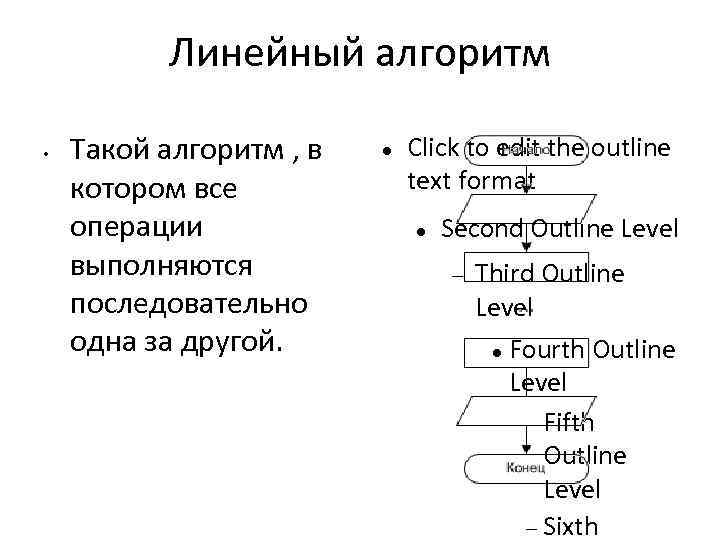Линейный алгоритм • Такой алгоритм , в котором все операции выполняются последовательно одна за другой. Click to edit the outline text format Second Outline Level Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

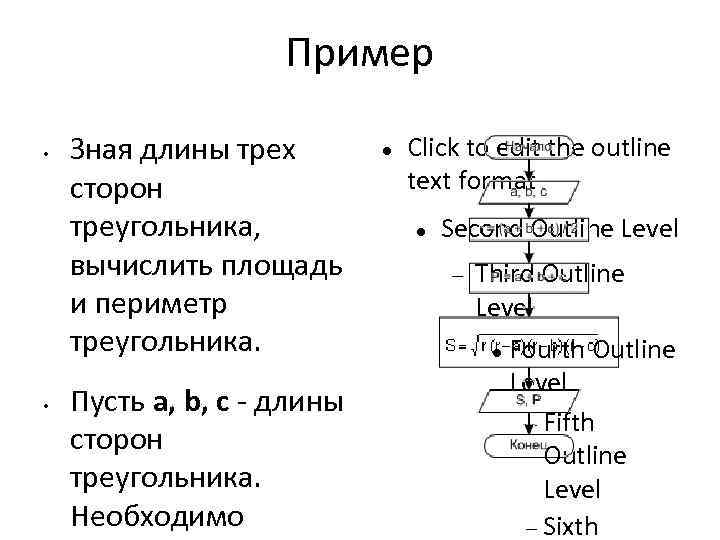Пример • • Зная длины трех сторон треугольника, вычислить площадь и периметр треугольника. Пусть a, b, c - длины сторон треугольника. Необходимо Click to edit the outline text format Second Outline Level Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

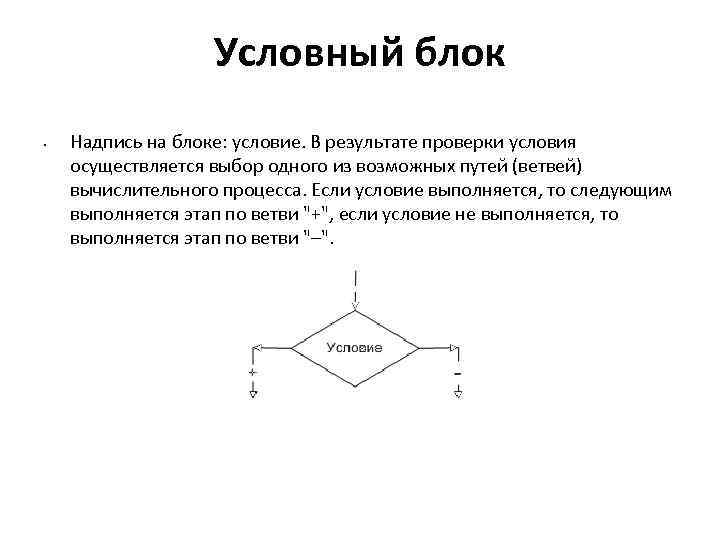Условный блок • Надпись на блоке: условие. В результате проверки условия осуществляется выбор одного из возможных путей (ветвей) вычислительного процесса. Если условие выполняется, то следующим выполняется этап по ветви "+", если условие не выполняется, то выполняется этап по ветви "–".

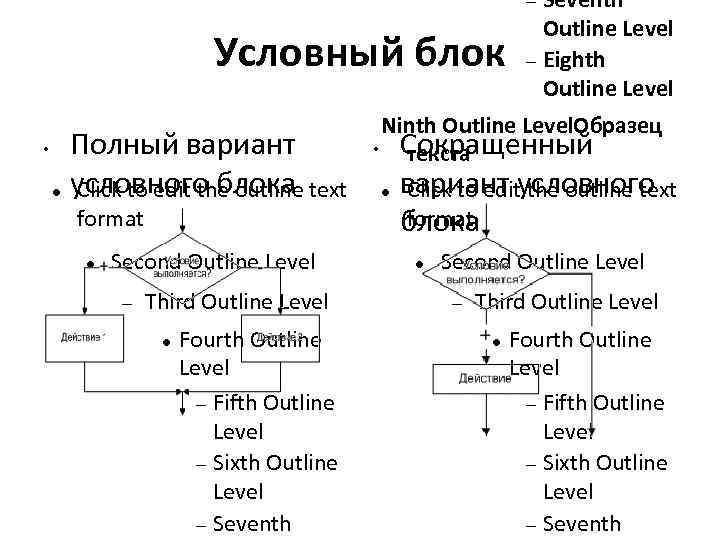Seventh Outline Level Eighth Outline Level Условный блок • Ninth Outline Level. Образец Полный вариант • Сокращенный текста условного блока Click to edit the outline text вариант условного Click to edit the outline text format блока Second Outline Level Third Outline Level Fourth Outline Level Fifth Outline Level Sixth Outline Level Seventh

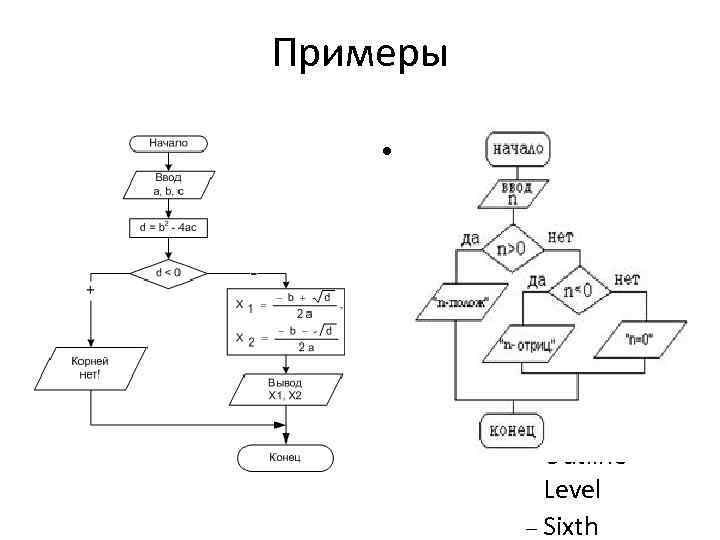Примеры Click to edit the outline text format Second Outline Level Third Outline Level Fourth Outline Level Fifth Outline Level Sixth

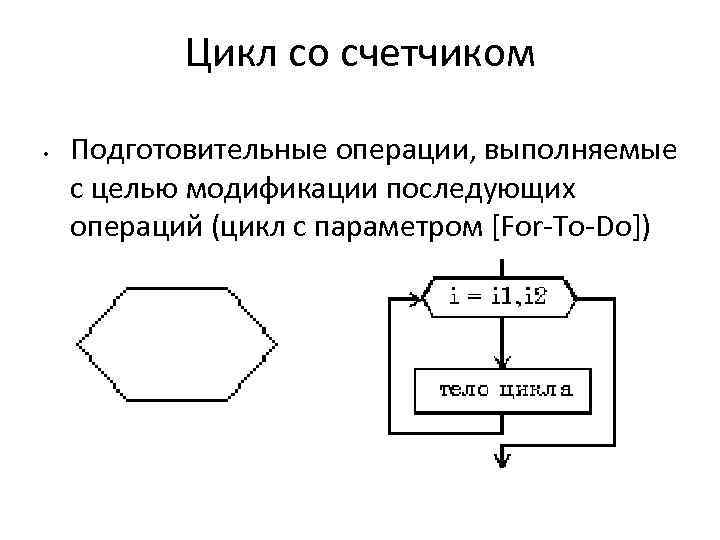Цикл со счетчиком • Подготовительные операции, выполняемые с целью модификации последующих операций (цикл с параметром [For-To-Do])

Цикл • Начало и конец цикла. Особенности работы цикла (инициализация, приращение, условие) записывается в начале или конце, в зависимости от того, где осуществляется его проверка (циклы с пред- или постусловием)

Примеры • • Пример1 Возвести число а в степень b используя цикл Пример2 найти значения функции y=x*x, c на интервале (а, b), c шагом с используя цикл с условием

Seventh Outline Level Eighth Outline Level А так же! • • Ninth Outline Level. Образец Дополнительные • Правила текста блоки Параллельные действия Click to edit the outline text • Допускается Click to edit the outline text format Second Outline Level • • Third Outline Level Поток данных или Fourth Outline управления Level Fifth Outline Level Sixth Outline Level Комментарии Seventh зеркально Second Outline Level отображать Third Outline Level символы и Fourth Outline поворачивать их Level вокруг оси. В Fifth Outline частности, Level Sixth Outline запоминающие Level устройства с Seventh

Псевдокод • Алгоритм поиска максимального элемента массива • Click to edit the outline Max. S (S, n; Max) text format Max = S[1] For I = 2 to n Second Outline Level if Max < S[i] Third Outline then Max = S[i] Level end for Fourth Outline return Max Level End Fifth Outline Level Sixth

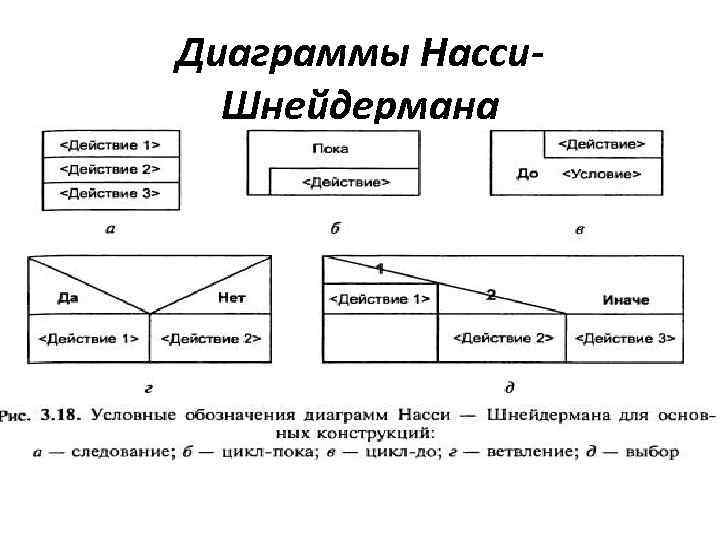Диаграммы Насси. Шнейдермана

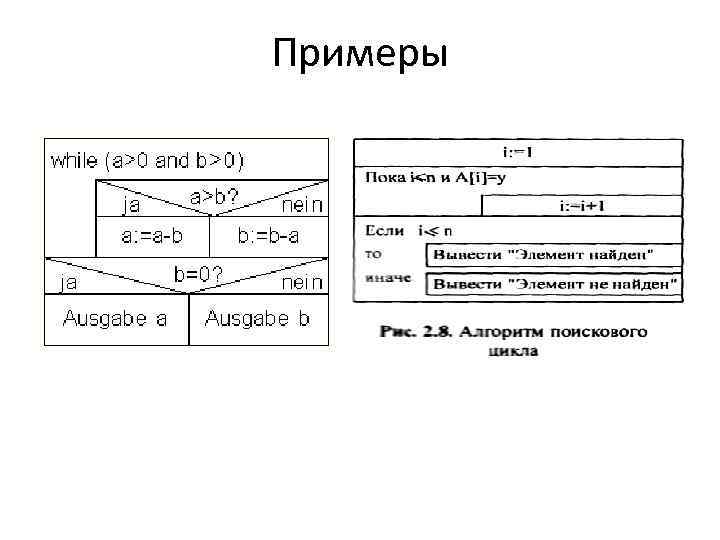Примеры

Преимущества • • • Запись является более компактной Изобразив алгоритм или программу в виде диаграммы Насси — Шнейдермана, можно быть гарантировано уверенным в том, что принципы структурного программирования соблюдены Диаграммы Насси — Шнейдермана удобнее использовать для пошаговой детализации задачи

Анализ трудоемкости алгоритмов

Анализ трудоемкости алгоритмов • При анализе алгоритма выбор входных данных может существенно повлиять на его выполнение. Скажем, некоторые алгоритмы сортировки могут работать очень быстро, если входной список уже отсортирован, тогда как другие алгоритмы покажут весьма скромный результат на таком списке. А вот на случайном списке результат может оказаться противоположным.

Лучший и худший случай • • Худший случай - Такой набор данных представляет собой комбинацию значений, на которой алгоритм выполняет меньше всего действий. Лучший случай- Такой набор данных представляет собой комбинацию значений, на которой алгоритм выполняет меньше всего действий.

Средний случай 1 В основе анализа лежит определение различных групп, на которые следует разбить возможные входные наборы данных. 2 На втором шаге определяется вероятность, с которой входной набор данных принадлежит каждой группе. 3 На третьем шаге подсчитывается время работы алгоритма на данных из каждой группы.

Средний случай • • Среднее время работы вычисляется по формуле: где через n обозначен размер входных данных, через т — число групп. p —

Трудоемкость • • Трудоемкость алгоритма - количество элементарных операций, которые необходимо выполнить для решения задачи с помощью данного алгоритма. Функция трудоемкости - отношение, связывающие входные данные алгоритма с количеством элементарных операций. Будем обозначать трудоемкость F

Элементарные операции в языке В качестве «элементарных» операций предлагается записи алгоритмов использовать следующие: • • Простое присваивание: а = b; • Одномерная индексация a[i]; • Арифметические операции: (*, /, -, +); • Операции сравнения: a < b(>, >=, <=, ==, !=); • Логические операции {or, and, not};

• Классификация алгоритмов по 1. Количественно-зависимые по виду функции трудоёмкости трудоемкости алгоритмы - Это алгоритмы, функция трудоемкости которых зависит только от размерности конкретного входа, и не зависит от конкретных значений • 2. Параметрически-зависимые по трудоемкости алгоритмы - Это алгоритмы, трудоемкость которых определяется не размерностью входа (как правило, для этой

Базовые конструкции при анализе трудоемкости Конструкция «Следование» • F=F 1+F 2 Конструкция «Ветвление» • F=p*F 1+(1 -p)F 2 Конструкция «Цикл» • F=1+3*N+N*Fтело

Пример 1 Задача суммирования элементов квадратной матрицы • Sum. M (A, n; Sum) Sum = 0 For i = 1 to n For j = 1 to n Sum = Sum + A[i, j] end for Return (Sum) End

• Пример 2 Задача поиска Max. S (S, n; Max) максимума в массиве Max <-- S[1] For i <-- 2 to n if Max < S[i] then Max <-- S[i] end for return Max End

Прочитать к лекции 2 • • Макконнелл, Дж. Основы современных алгоритмов [Текст] / Дж. Макконнелл. – М. : Техносфера, 2006. – 366 с. – глава 1 (1. 51. 7)(+ Глава 2) Кормен (Введение(упор), Глава 1 бегом)