 Алгоритмы 1 курс, 2 семестр, 3 лекция 1
Алгоритмы 1 курс, 2 семестр, 3 лекция 1
 Литература 1. 2. 3. Стойлова Л. П. Математика. – М. : Академия, 2007. , стр. 150 -162. Лыфенко А. В. Математика. Методическое пособие для организации тематического и итогового контроля знаний студентов факультета начального образования. – Калуга: КГПУ, 2008. Л. П. Стойлова, Г. В. Хамер Алгоритмы и их свойства. Метод. рекомендации к сам. работе над курсом математики. М. : МГОПИ, 1994. 2
Литература 1. 2. 3. Стойлова Л. П. Математика. – М. : Академия, 2007. , стр. 150 -162. Лыфенко А. В. Математика. Методическое пособие для организации тематического и итогового контроля знаний студентов факультета начального образования. – Калуга: КГПУ, 2008. Л. П. Стойлова, Г. В. Хамер Алгоритмы и их свойства. Метод. рекомендации к сам. работе над курсом математики. М. : МГОПИ, 1994. 2
 План 1. 2. 3. 4. 5. Понятие «алгоритм» . Свойства алгоритмов. Способы записи алгоритмов. Виды алгоритмов. Приемы построения алгоритмов. 3
План 1. 2. 3. 4. 5. Понятие «алгоритм» . Свойства алгоритмов. Способы записи алгоритмов. Виды алгоритмов. Приемы построения алгоритмов. 3
 Понятие «алгоритм» Колмогоров Андрей Николаевич (1903 1987) отечественный математик А лан Матисон Тью ринг Абу Абдулла Мухаммад ибн (англ. Alan Mathison Turing; Муса ал Хорезми (ок. 783 — 23 июня 1912 — 7 июня ок. 850) — великий 1954) — английский среднеазиатский математик, логик, астроном и географ. криптограф. 4
Понятие «алгоритм» Колмогоров Андрей Николаевич (1903 1987) отечественный математик А лан Матисон Тью ринг Абу Абдулла Мухаммад ибн (англ. Alan Mathison Turing; Муса ал Хорезми (ок. 783 — 23 июня 1912 — 7 июня ок. 850) — великий 1954) — английский среднеазиатский математик, логик, астроном и географ. криптограф. 4
 Понятие «алгоритм» Под алгоритмом будем понимать точное, понятное предписание о том, какие действия и в каком порядке необходимо выполнить, чтобы решить любую из данного класса однотипных задач. 5
Понятие «алгоритм» Под алгоритмом будем понимать точное, понятное предписание о том, какие действия и в каком порядке необходимо выполнить, чтобы решить любую из данного класса однотипных задач. 5
 Свойства алгоритмов 1. 2. 3. 4. 5. Детерминированность (определённость). Предписание должно быть однозначно осуществимо и не требует свободно понимаемых исполнителем решений. Понятность. Команды предписания должны входить в группу команд исполнителя, т. е. должны быть ему понятны. Результативность. Предписание позволяет решить задачу за конечное число шагов. Дискретность. Для каждого шага предписания существует не более одного следующего шага. Массовость. Предписание составляется для решения класса однотипных задач. 6
Свойства алгоритмов 1. 2. 3. 4. 5. Детерминированность (определённость). Предписание должно быть однозначно осуществимо и не требует свободно понимаемых исполнителем решений. Понятность. Команды предписания должны входить в группу команд исполнителя, т. е. должны быть ему понятны. Результативность. Предписание позволяет решить задачу за конечное число шагов. Дискретность. Для каждого шага предписания существует не более одного следующего шага. Массовость. Предписание составляется для решения класса однотипных задач. 6
 Свойства алгоритмов Детерминированность Понятность Результативность Дискретность Массовость Привести примеры двух трёх высказываний. Сложить 2 с любым их двузначных чисел. К 18 прибавить наименьшее из чисел 99, 102, 780. В одной деревне живет парикмахер, который может брить только тех, кто не бреется сам. Как ему поступить по отношению к себе? Какой алгоритм позволяет вычислить 456+98 95234+56 7
Свойства алгоритмов Детерминированность Понятность Результативность Дискретность Массовость Привести примеры двух трёх высказываний. Сложить 2 с любым их двузначных чисел. К 18 прибавить наименьшее из чисел 99, 102, 780. В одной деревне живет парикмахер, который может брить только тех, кто не бреется сам. Как ему поступить по отношению к себе? Какой алгоритм позволяет вычислить 456+98 95234+56 7
 Способы записи алгоритмов 1. 2. 3. 4. 5. Словесная запись. Запись в виде формулы. Запись в виде таблицы. На языке блок схем. На языках программирования. 8
Способы записи алгоритмов 1. 2. 3. 4. 5. Словесная запись. Запись в виде формулы. Запись в виде таблицы. На языке блок схем. На языках программирования. 8
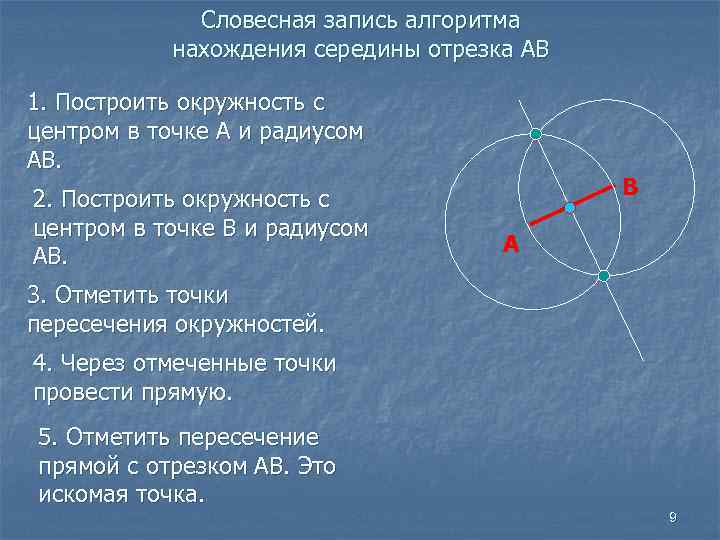 Словесная запись алгоритма нахождения середины отрезка АВ 1. Построить окружность с центром в точке А и радиусом АВ. 2. Построить окружность с центром в точке В и радиусом АВ. В А 3. Отметить точки пересечения окружностей. 4. Через отмеченные точки провести прямую. 5. Отметить пересечение прямой с отрезком АВ. Это искомая точка. 9
Словесная запись алгоритма нахождения середины отрезка АВ 1. Построить окружность с центром в точке А и радиусом АВ. 2. Построить окружность с центром в точке В и радиусом АВ. В А 3. Отметить точки пересечения окружностей. 4. Через отмеченные точки провести прямую. 5. Отметить пересечение прямой с отрезком АВ. Это искомая точка. 9
 Запись в виде формулы алгоритма решения квадратного уравнения 10
Запись в виде формулы алгоритма решения квадратного уравнения 10
 Запись в виде таблицы алгоритмического предписания решения задачи Задача: «В одном куске 72 м сатина, а в другом в а раз больше. Сколько метров сатина во втором кусе. Составьте выражение и найдите его значения при а=2, 4 6. » Словесная запись: 1. Составить выражение. 2. Найти значение выражения при а=2. 3. Найти значение выражения при а=4. 4. Найти значение выражения при а=6. Табличная запись: а 72 а 2 4 6 11
Запись в виде таблицы алгоритмического предписания решения задачи Задача: «В одном куске 72 м сатина, а в другом в а раз больше. Сколько метров сатина во втором кусе. Составьте выражение и найдите его значения при а=2, 4 6. » Словесная запись: 1. Составить выражение. 2. Найти значение выражения при а=2. 3. Найти значение выражения при а=4. 4. Найти значение выражения при а=6. Табличная запись: а 72 а 2 4 6 11
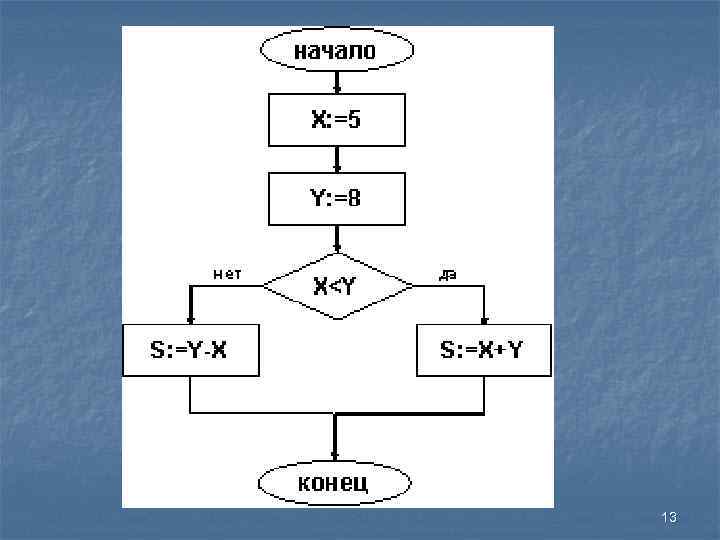
 Запись алгоритма на языке блок схем Блок Описание блока Обозначает начало и конец алгоритма. Внутри указываются слова «начало» или «конец» . Имеет один вход или один выход. Арифметический блок. Предусматривает выполнение некоторого действия, в результате которого образуется новый результат. Имеет один вход и один выход. Логический блок. Предусматривает проверку условия. Не приводит к новому результату, определяет дальнейший ход процесса. Имеет один вход и два выхода. 12
Запись алгоритма на языке блок схем Блок Описание блока Обозначает начало и конец алгоритма. Внутри указываются слова «начало» или «конец» . Имеет один вход или один выход. Арифметический блок. Предусматривает выполнение некоторого действия, в результате которого образуется новый результат. Имеет один вход и один выход. Логический блок. Предусматривает проверку условия. Не приводит к новому результату, определяет дальнейший ход процесса. Имеет один вход и два выхода. 12
 13
13
 Запись алгоритма на языках программирования var n, i, S : integer; BEGIN n: =15; S: =0; for i=1 to n do if i mod 7 =0 then S: =S+i; writeln (S); END. 14
Запись алгоритма на языках программирования var n, i, S : integer; BEGIN n: =15; S: =0; for i=1 to n do if i mod 7 =0 then S: =S+i; writeln (S); END. 14
 Какие способы записи алгоритмов использует автор в заданиях? Задания взяты из учебника А. В. Горячева Информатика в играх и задачах 3 класс, 2 часть. 15
Какие способы записи алгоритмов использует автор в заданиях? Задания взяты из учебника А. В. Горячева Информатика в играх и задачах 3 класс, 2 часть. 15
 Виды алгоритмов n n n Линейный. Действия выполняются последовательно друг за другом (Нахождение середины отрезка). Разветвляющийся (условный). Выполнение действий зависит от некоторого условия (решение квадратного уравнения). Циклический. Группа команд выполняется многократно (пример алгоритма на языке ПАСКАЛЬ). 16
Виды алгоритмов n n n Линейный. Действия выполняются последовательно друг за другом (Нахождение середины отрезка). Разветвляющийся (условный). Выполнение действий зависит от некоторого условия (решение квадратного уравнения). Циклический. Группа команд выполняется многократно (пример алгоритма на языке ПАСКАЛЬ). 16
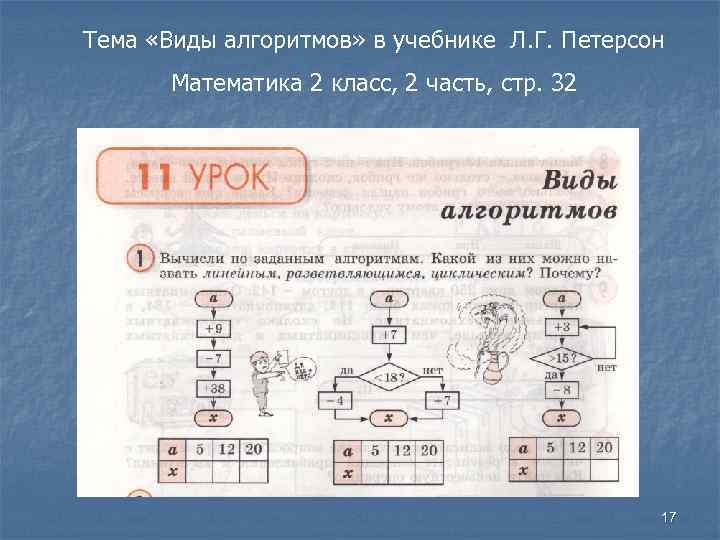 Тема «Виды алгоритмов» в учебнике Л. Г. Петерсон Математика 2 класс, 2 часть, стр. 32 17
Тема «Виды алгоритмов» в учебнике Л. Г. Петерсон Математика 2 класс, 2 часть, стр. 32 17
 Приемы построения алгоритмов n n Прием пошаговой детализации. Построение алгоритма на основе решения частных задач. 18
Приемы построения алгоритмов n n Прием пошаговой детализации. Построение алгоритма на основе решения частных задач. 18
 Построение алгоритма путем пошаговой детализации I. III. Построение алгоритма в крупных блоках. Определение последовательности выполнения блоков. Уточнение блоков до тех пор, пока они не станут понятны исполнителю. 19
Построение алгоритма путем пошаговой детализации I. III. Построение алгоритма в крупных блоках. Определение последовательности выполнения блоков. Уточнение блоков до тех пор, пока они не станут понятны исполнителю. 19
 Построение алгоритма решения простейших уравнений Определение блоков. Назвать неизвестный компонент, прочитать уравнение, использовать правило нахождения компонента, вычислить, сделать проверку. I. Упорядочивание блоков. 1. Прочитай уравнение. 2. Вспомни правило нахождения неизвестного компонента. 3. Найди корень уравнения. 4. Сделай проверку. 5. Запиши ответ. II. Детализация блоков. Детализация блока 1. 1) Назови действие, которое указано в уравнении. 2) Вспомни , как называются компоненты действия. 3) Прочитай уравнение, используя название компонентов. I. 20
Построение алгоритма решения простейших уравнений Определение блоков. Назвать неизвестный компонент, прочитать уравнение, использовать правило нахождения компонента, вычислить, сделать проверку. I. Упорядочивание блоков. 1. Прочитай уравнение. 2. Вспомни правило нахождения неизвестного компонента. 3. Найди корень уравнения. 4. Сделай проверку. 5. Запиши ответ. II. Детализация блоков. Детализация блока 1. 1) Назови действие, которое указано в уравнении. 2) Вспомни , как называются компоненты действия. 3) Прочитай уравнение, используя название компонентов. I. 20
 Построение алгоритма на основе решения частных задач I. III. IV. Анализ частных задач, приводящих к разным результатам. Выявление операций и их последовательности при решении частных задач. Выявление всех условий, приводящих к разным результатам. Окончательное построение алгоритма. 21
Построение алгоритма на основе решения частных задач I. III. IV. Анализ частных задач, приводящих к разным результатам. Выявление операций и их последовательности при решении частных задач. Выявление всех условий, приводящих к разным результатам. Окончательное построение алгоритма. 21
 Построение алгоритма решения уравнений вида ах=в I. Анализ частных задач (3 х=12, 2 х=5, 4 х=0, 2 х=2, 0 х=5, 0 х= 12, 0 х=0). II. Выявление операций (деление в на а, не содержит операций). III. Выявление всех условий (если а≠ 0, то х=в: а; если а=0 и в≠ 0, то Ø; если а=0 и в=0, то корней бесконечно много). IV. Окончательное построение алгоритма. 22
Построение алгоритма решения уравнений вида ах=в I. Анализ частных задач (3 х=12, 2 х=5, 4 х=0, 2 х=2, 0 х=5, 0 х= 12, 0 х=0). II. Выявление операций (деление в на а, не содержит операций). III. Выявление всех условий (если а≠ 0, то х=в: а; если а=0 и в≠ 0, то Ø; если а=0 и в=0, то корней бесконечно много). IV. Окончательное построение алгоритма. 22
 23
23
 Типовые задания для подготовки к практическому занятию n n Составьте алгоритм вычисления по формуле: у = (5 х 3) · (2 х+7); По приведенному алгоритму восстановите формулу для вычисления значения у: 1. 2. 3. Умножить х на 4, обозначить результат R 1. Сложить R 1 с числом 7, обозначить результат R 2. Разделить R 2 на х, считать резуль тат значением у. 24
Типовые задания для подготовки к практическому занятию n n Составьте алгоритм вычисления по формуле: у = (5 х 3) · (2 х+7); По приведенному алгоритму восстановите формулу для вычисления значения у: 1. 2. 3. Умножить х на 4, обозначить результат R 1. Сложить R 1 с числом 7, обозначить результат R 2. Разделить R 2 на х, считать резуль тат значением у. 24
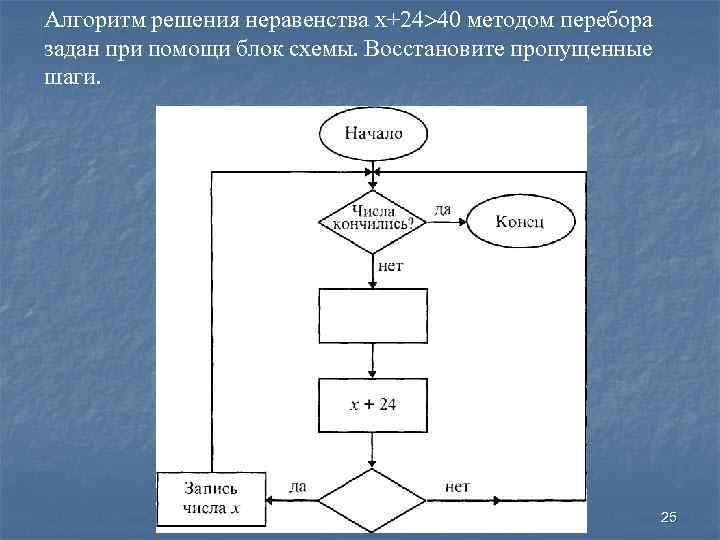 Алгоритм решения неравенства х+24 40 методом перебора задан при помощи блок схемы. Восстановите пропущенные шаги. 25
Алгоритм решения неравенства х+24 40 методом перебора задан при помощи блок схемы. Восстановите пропущенные шаги. 25


