Алгоритми сортування Алгоритми сортування Алгоритмом сортування називається

Алгоритми сортування

Алгоритми сортування Алгоритмом сортування називається алгоритм для впорядкування деякої множини елементів. Зазвичай під алгоритмом сортування розуміють алгоритм впорядкування множини елементів за зростанням або спаданням. У разі наявності елементів з однаковими значеннями, в упорядкованій послідовності вони розташовуються поруч один за одним в будь-якому порядку. Однак іноді буває корисно зберігати первісний порядок елементів з однаковими значеннями. В алгоритмах сортування лише частина даних використовується в якості ключа сортування. Ключем сортування називається атрибут (або декілька атрибутів), за значенням якого визначається порядок елементів. Таким чином, при написанні алгоритмів сортувань масивів слід врахувати, що ключ повністю або частково збігається з даними. Практично кожен алгоритм сортування можна розбити на 3 частини: • порівняння, що визначає впорядкованість пари елементів; • перестановку, яка міняє місцями пару елементів; • власне алгоритм сортування, який здійснює порівняння і перестановку елементів до тих пір, поки всі елементи множини не будуть упорядковані.

Алгоритми сортування мають широке практичне застосування. Їх можна зустріти там, де мова йде про обробку і зберіганні великих об’ємів інформації. Деякі завдання обробки даних вирішуються простіше, якщо дані заздалегідь упорядкувати. Оцінка алгоритмів сортування Жодна інша проблема не породила такої кількості найрізноманітніших рішень, як завдання сортування. Універсального, найкращого алгоритму сортування на даний момент не існує. Однак, маючи характеристики вхідних даних, можна підібрати метод, який працює оптимальним чином. Для цього необхідно знати параметри, за якими буде здійснюватися оцінка алгоритмів.

Алгоритми сортування Час сортування - основний параметр, що характеризує швидкодію алгоритму. Пам'ять - один з параметрів, який характеризується тим, що ряд алгоритмів сортування вимагають виділення додаткової пам'яті під тимчасове зберігання даних. При оцінці використовуваної пам'яті не буде враховуватися місце, яке займає вихідний масив даних і витрати пов’язані з вхідною інформацією, наприклад, зберігання коду програми. Стійкість - це параметр, який відповідає за те, що сортування не змінює взаємного розташування рівних елементів. Природність поведінки - параметр, який вказує на ефективність методу при обробці вже відсортованих, або частково відсортованих даних. Алгоритм поводиться природно, якщо враховує цю характеристику вхідної послідовності і працює краще.

Алгоритми сортування Класифікація алгоритмів сортувань Все розмаїття алгоритмів сортувань можна класифікувати за різними ознаками, наприклад, за стійкістю, за використанням операцій порівняння, за потребами у додатковій пам'яті, за потребами в знаннях про структуру даних, що виходять за рамки операції порівняння, та інші. Найдетальніше розглянемо класифікацію алгоритмів сортування за сферою застосування. У такому випадку основні типи сортування діляться наступним чином. Внутрішнє сортування - це алгоритм сортування, який в процесі впорядкування даних використовує тільки оперативну пам'ять (ОП) комп'ютера. Тобто оперативної пам'яті достатньо для розміщення в ній сортованого масиву даних з довільним доступом до будь-якої комірки і для виконання алгоритму. Внутрішнє сортування застосовується у всіх випадках, за винятком однопрохідного зчитування даних і однопрохідного запису відсортованих даних. Залежно від конкретного алгоритму і його реалізації дані можуть сортуватися в тій же області пам'яті, або використовувати додаткову оперативну пам'ять.

Алгоритми сортування Зовнішнє сортування - це алгоритм сортування, який при проведенні впорядкування даних використовує зовнішню пам'ять, як правило, жорсткі диски. Зовнішнє сортування розроблене для обробки великих списків даних, які не можна розмістити в оперативній пам'яті. Звернення до різних носіїв накладає деякі додаткові обмеження на такий алгоритм: доступ до носія здійснюється послідовним чином, тобто в кожен момент часу можна зчитати або записати тільки елемент, наступний за поточним; об'єм даних не дозволяє їм розміститися в ОП. Внутрішнє сортування є базовим для будь-якого алгоритму зовнішнього сортування - окремі частини масиву даних сортуються в оперативній пам'яті і за допомогою спеціального алгоритму складаються в один масив, упорядкований за ключем. Слід зазначити, що внутрішнє сортування є значно ефективнішим за зовнішнє, так як на звернення до оперативної пам'яті витрачається набагато менше часу, ніж до носіїв.

Алгоритми сортування Розглянемо основні алгоритми внутрішного сортування, які називаються удосконаленими (логарифмічними). Бінарне пірамідальне сортування Цей метод сортування був запропонований Дж. Уільямсом і Р. Флойдом в 1964 році. Алгоритм пірамідального сортування англійською називається «Heap Sort» . «Heap» перекладається, як «купа» . У зв'язку з цим пірамідальне сортування ще називають «сортування купою» . Пірамідальне сортування у деякому сенсі є модифікацією такого підходу, як сортування вибором, з тією лише відмінністю, що мінімальний (або максимальний) елемент з невідсортованої послідовності вибирається за меншу кількість операцій. Для можливості такого швидкого вибору з невідсортованої послідовності будується певна структура. Суть методу і полягає в побудові такої структури, яка називається пірамідою.

Алгоритми сортування Піраміда (сортувальне дерево, двійкова купа) - двійкове дерево з впорядкованими листям (корінь дерева - найменший чи найбільший елемент). Піраміду можна представити у вигляді масиву. Перший елемент піраміди є найменшим або найбільшим, що залежить від ключа сортування. Просіювання - це побудова нової піраміди за наступним алгоритмом: новий елемент розміщується у вершину дерева, далі він переміщається ("просівається") по дорозі вниз на основі порівняння з дочірніми елементами. Спуск завершується, якщо результат порівняння з дочірніми елементами відповідає ключу сортування. Послідовність чисел xi, xi +1 , . . . , xi формує піраміду, якщо для всіх k = i, i +1 , . . . , n / 2 виконуються нерівності xk>= x 2 k, xk>= x 2 k+1 (або xk <=x 2 k, xk <=x 2 k +1). Елементи x 2 i і x 2 i +1 називаються нащадками елемента xi. Масив чисел 12 10 7 5 8 7 3 є пірамідою. Такий масив зручно зображати у вигляді дерева. Перший елемент масиву, елементи якого утворюють собою піраміду, є найбільшим (або найменшим). Якщо масив представлений у вигляді піраміди, то масив легко відсортувати.

Алгоритми сортування Ідея алгоритму Піраміда - двійкове дерево, в якому значення кожного елемента більше або дорівнює значень дочірніх елементів. Заповнивши дерево елементами в довільному порядку, можна легко його відсортувати (легше, ніж вихідний список елементів), перетворивши на піраміду Найбільший елемент піраміди знаходиться в її вершині Відокремлюємо вершинний елемент, і записуємо його в кінець результуючого масиву На місце елемента у вершині записуємо елемент з самого нижнього рівня дерева Відновлюємо (пересортовуємо) піраміду. Найбільший елемент з решти знову у вершині. Знову відокремлюємо його і записуємо його в якості передостаннього елемента результату, і так далі Весь фокус алгоритму в тому, що піраміда без додаткових витрат зберігається прямо у вихідному масиві. У міру того, як розмір піраміди зменшується, вона займає все меншу частину масиву, а результат сортування записується починаючи з кінця масиву на звільнені від піраміди місця.

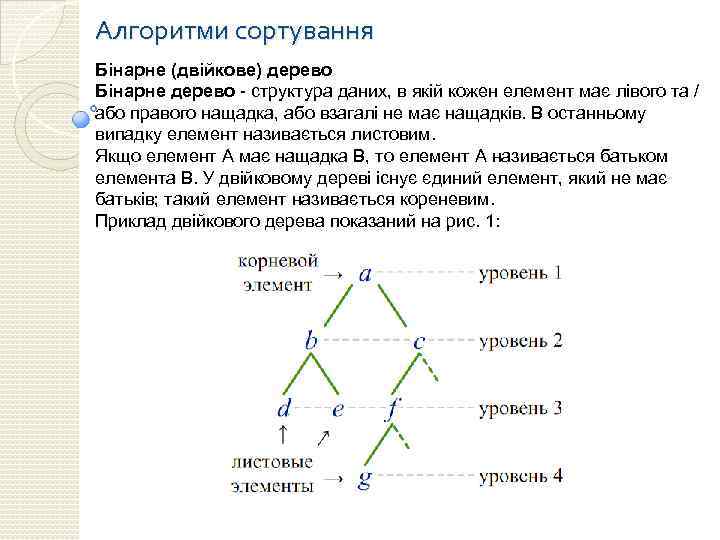Алгоритми сортування Бінарне (двійкове) дерево Бінарне дерево - структура даних, в якій кожен елемент має лівого та / або правого нащадка, або взагалі не має нащадків. В останньому випадку елемент називається листовим. Якщо елемент A має нащадка B, то елемент A називається батьком елемента B. У двійковому дереві існує єдиний елемент, який не має батьків; такий елемент називається кореневим. Приклад двійкового дерева показаний на рис. 1:

Алгоритми сортування Майже заповненим двійковим деревом називається бінарне дерево, що володіє трьома властивостями: 1) всі листові елементи знаходяться в нижньому рівні, або в нижніх двох рівнях; 2) все листя у рівні заповнює рівень зліва; 3) всі рівні (крім, можливо, останнього рівня) повністю заповнені елементами. Дерево на рис. 1 не є майже заповненим, тому що рівень 4 не заповнений ліворуч (елемент g «заважає» ), і третій рівень (який не є останнім), не є заповненим повністю. Майже заповнене двійкове дерево можна зберігати в масиві без додаткових витрат. Для цього достатньо перенумерувати елементи кожного рівня зліва-направо:

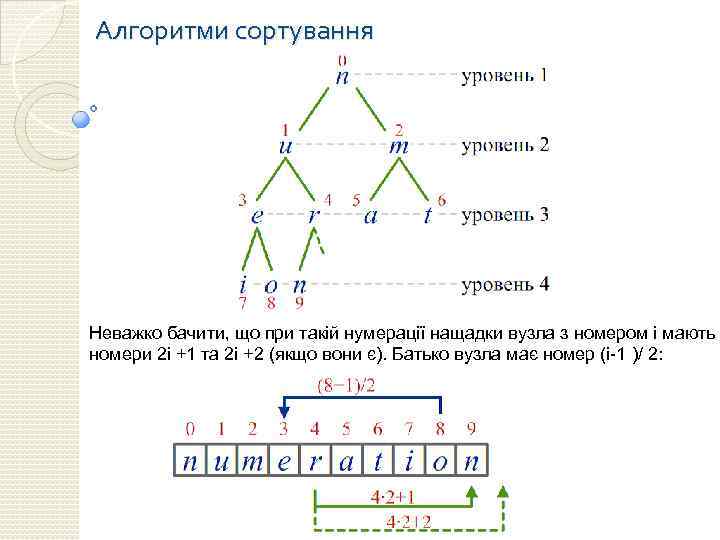Алгоритми сортування Неважко бачити, що при такій нумерації нащадки вузла з номером i мають номери 2 i +1 та 2 i +2 (якщо вони є). Батько вузла має номер (i-1 )/ 2:

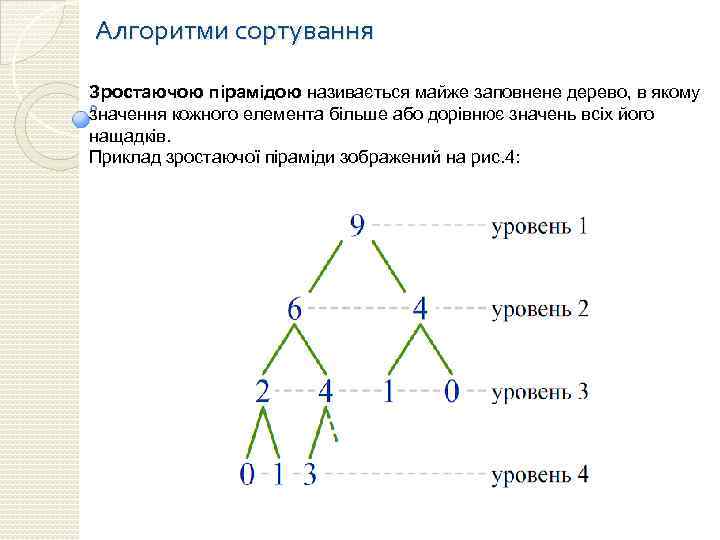Алгоритми сортування Зростаючою пірамідою називається майже заповнене дерево, в якому значення кожного елемента більше або дорівнює значень всіх його нащадків. Приклад зростаючої піраміди зображений на рис. 4:

Алгоритми сортування Очевидно, що найбільше значення в зростаючій піраміді має кореневий елемент. Однак, з властивостей піраміди не випливає, що значення елементів зменшуються зі збільшенням рівня. Зокрема, на малюнку 4 елемент зі значенням 3 на четвертому рівні є більшим за значення всіх елементів, крім одного, що знаходяться на третьому рівні. Важливою операцією є відділення останнього (у сенсі нумерації) елемента від піраміди. Неважко довести, що в цьому випадку двійкове дерево залишається майже заповненим, і всі властивості піраміди зберігаються. Розглянемо тепер задачу приєднання елемента з довільним значенням до зростаючої піраміді. Якщо просто додати елемент в кінець масиву, то властивість піраміди (значення будь-якого елементу <= значення його батька) може бути порушено.

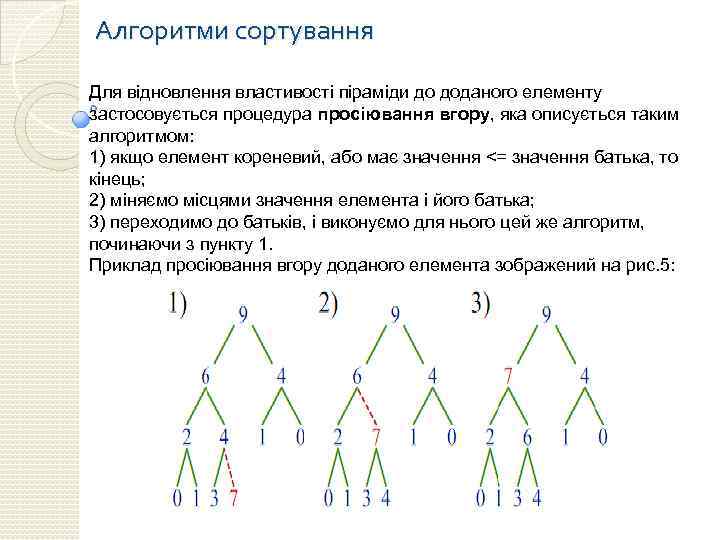Алгоритми сортування Для відновлення властивості піраміди до доданого елементу застосовується процедура просіювання вгору, яка описується таким алгоритмом: 1) якщо елемент кореневий, або має значення <= значення батька, то кінець; 2) міняємо місцями значення елемента і його батька; 3) переходимо до батьків, і виконуємо для нього цей же алгоритм, починаючи з пункту 1. Приклад просіювання вгору доданого елемента зображений на рис. 5:

Алгоритми сортування Після виконання цієї процедури властивість піраміди буде відновлено. Якщо знову доданий елемент є більшим за батька, то він є більшим і другого нащадка батька (якщо другий нащадок є), так як до додавання нового елемента було виконано властивість піраміди, і батько був не меншим за свого нащадка (на малюнку 5 ліворуч: сімка є більшою за свого батька - четвірку, - тому вона є більшою і за другого нащадка четвірки - трійки). Після обміну значень елемента і батька властивість піраміди буде відновлено в піддереві, коренем якого є батько з новим значенням (наприклад, після обміну місцями сімки і четвірки, сімка трійка і четвірка будуть утворювати правильне піддерево).

Алгоритми сортування Просіювання вниз Що робити, якщо нам потрібно замінити кореневий елемент на якийнебудь інший? У цьому випадку пірамідальну структуру двійкового дерева можна відновити за допомогою процедури просіювання вниз: 1) якщо елемент має значення >= значень нащадків, то кінець; 2) інакше міняємо місцями значення елемента і його нащадка, що має максимальне значення; 3) переходимо до зміненого нащадку, і виконуємо для нього цей же алгоритм, починаючи з пункту 1. Приклад просіювання вниз зображений на рис. 6:

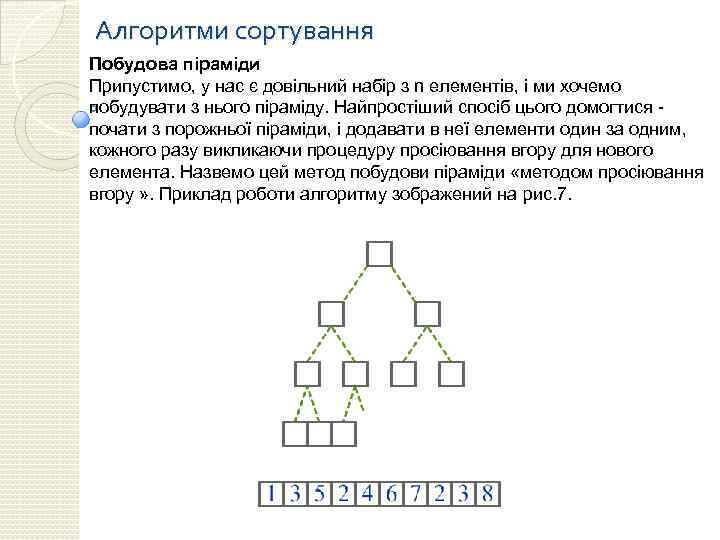Алгоритми сортування Побудова піраміди Припустимо, у нас є довільний набір з n елементів, і ми хочемо побудувати з нього піраміду. Найпростіший спосіб цього домогтися - почати з порожньої піраміди, і додавати в неї елементи один за одним, кожного разу викликаючи процедуру просіювання вгору для нового елемента. Назвемо цей метод побудови піраміди «методом просіювання вгору » . Приклад роботи алгоритму зображений на рис. 7.

Алгоритми сортування Сортування Маючи побудовану піраміду, нескладно реалізувати сортування. Так як кореневий елемент піраміди має найбільше значення, ми можемо відокремити його і помістити в відсортований список. Замість відсутнього кореневого елемента можна поставити останній (в сенсі нумерації) елемент дерева і, просіявши його вниз, знову отримати піраміду. У новій зменшеній піраміді корінь має найбільше значення серед елементів, що залишилися. Його знову можна відокремити і помістити в відсортований список перед наявними там елементами, і так далі. Алгоритм є неефективний, тому, що на місце відсутнього кореневого елемента ставиться елемент з останнього рівня піраміди. Елементи останнього рівня мають малі значення, тому, ставлячи елемент з останнього рівня на місце кореневого елемента ми, швидше за все, будемо змушені просівати його в самий низ піраміди. Насправді запропонований спосіб - найпростіший і найшвидший (в тому сенсі, що нічого кращого поки не придумано) з усіх можливих способів відновити піраміду з відсутнім кореневим елементом.

Алгоритми сортування Для зберігання відсортованого списку будемо використовувати елементи вихідного масиву, що звільняються в результаті зменшення розміру піраміди. Алгоритм виходить наступний: • поміняти місцями значення першого і останнього елементів піраміди; • відокремити останній елемент від дерева, зменшивши розмір дерева на одиницю (елемент залишається в масиві); • відновити піраміду, просіявши вниз її новий кореневий елемент; • перейти до пункту 1; Після закінчення роботи алгоритму, частина масиву, зайнята деревом, зменшується, а в кінці масиву накопичується відсортований результат. Реалізація пірамідального сортування на мовах програмування наведена на багатьох інтернет-ресурсах.

Алгоритми сортування Сортування методом Шелла було названо на честь її винахідника - Дональда Шелла, який опублікував цей алгоритм у 1959 році. Загальна ідея сортування Шелла полягає в порівнянні на початкових стадіях сортування пар значень, розташованих досить далеко один від одного в наборі даних, що впорядковується. Така модифікація методу сортування дозволяє швидко переставляти далекі невпорядковані пари значень (сортування таких пар зазвичай вимагає великої кількості перестановок, якщо використовується порівняння тільки сусідніх елементів).

Алгоритми сортування Швидке сортування Хоара Метод швидкого сортування був вперше описаний Ч. А. Р. Хоаром в 1962 році. Швидке сортування - це загальна назва ряду алгоритмів, які відображають різні підходи до одержання критичного параметра, що впливає на продуктивність методу. При загальному розгляді алгоритму швидкого сортування, відзначимо, що цей метод грунтується на послідовному поділі сортованого набору даних на блоки меншого розміру таким чином, що між значеннями різних блоків забезпечується впорядкованість (для будь-якої пари блоків всі значення одного з цих блоків не перевищують значень іншого блоку ). Опорним (провідним) елементом називається певний елемент масиву, який вибирається у певний спосіб. З точки зору коректності алгоритму вибір опорного елемента не має значення. З точки зору підвищення ефективності алгоритму вибиратися повинна медіана, але без додаткових відомостей про сортування даних її зазвичай неможливо отримати. Необхідно вибирати постійно один і той же елемент (наприклад, середній або останній за положенням) або вибирати елемент з випадково вибраним індексом.

Алгоритми сортування Сортування злиттям Алгоритм сортування злиттям був винайдений Джоном фон Нейманом в 1945 році. Він вважається одним з найшвидших способів сортування. Злиття - це об'єднання двох або більше упорядкованих масивів в один упорядкований. Сортування злиттям є одним з найпростіших алгоритмів сортування (серед швидких алгоритмів). Особливістю цього алгоритму є те, що він працює з елементами масиву переважно послідовно, завдяки чому саме цей алгоритм використовується при сортуванні в системах з різними апаратними обмеженнями (наприклад, під час сортування даних на жорсткому диску). Крім того, сортування злиттям є алгоритмом, який може бути ефективно використаним для сортування таких структур даних, як зв'язані списки. Цей алгоритм застосовується тоді, коли є можливість використовувати для зберігання проміжних результатів пам'ять, порівнянну з розміром вихідного масиву. Він побудований на принципі "розділяй і володарюй". Спочатку завдання розбивається на кілька підзадач меншого розміру. Потім ці завдання розв’язуються за допомогою рекурсивного виклику або безпосередньо, якщо їх розмір досить малий. Далі їх розв'язки комбінуються, що дає розв'язок вихідної задачі. Процедура злиття вимагає наявності двох відсортованих масивів. Зауважимо, що масив з одного елемента за визначенням є відсортованим.

Алгоритми сортування Сортування злиттям Алгоритм сортування злиттям був винайдений Джоном фон Нейманом в 1945 році. Він вважається одним з найшвидших способів сортування. Злиття - це об'єднання двох або більше упорядкованих масивів в один упорядкований. Сортування злиттям є одним з найпростіших алгоритмів сортування (серед швидких алгоритмів). Особливістю цього алгоритму є те, що він працює з елементами масиву переважно послідовно, завдяки чому саме цей алгоритм використовується при сортуванні в системах з різними апаратними обмеженнями (наприклад, під час сортування даних на жорсткому диску). Крім того, сортування злиттям є алгоритмом, який може бути ефективно використаним для сортування таких структур даних, як зв'язані списки. Цей алгоритм застосовується тоді, коли є можливість використовувати для зберігання проміжних результатів пам'ять, порівнянну з розміром вихідного масиву. Він побудований на принципі "розділяй і володарюй". Спочатку завдання розбивається на кілька підзадач меншого розміру. Потім ці завдання розв’язуються за допомогою рекурсивного виклику або безпосередньо, якщо їх розмір досить малий. Далі їх розв'язки комбінуються, що дає розв'язок вихідної задачі.

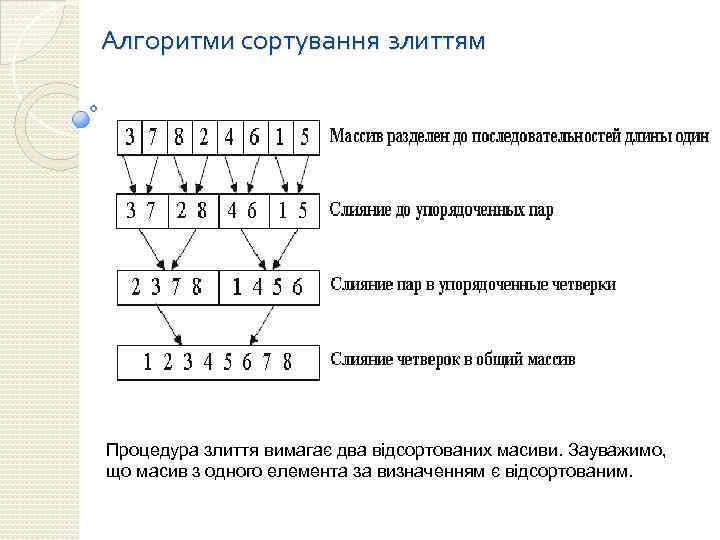Алгоритми сортування злиттям Процедура злиття вимагає два відсортованих масиви. Зауважимо, що масив з одного елемента за визначенням є відсортованим.

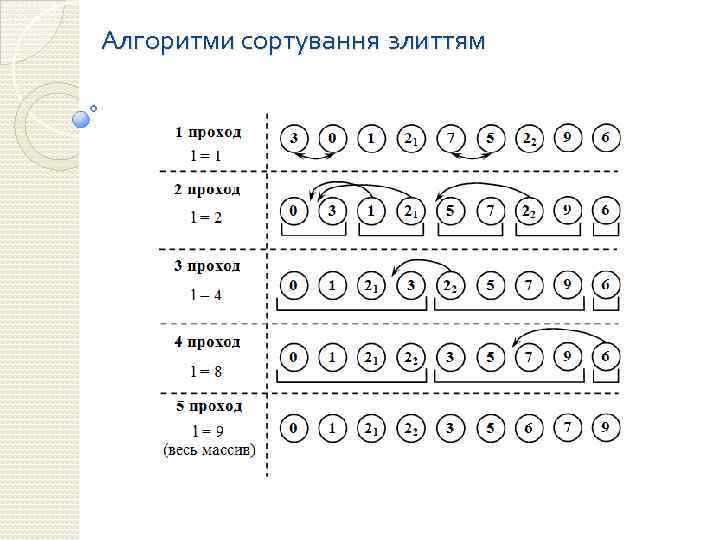
Алгоритми сортування злиттям Алгоритм сортування злиттям Крок 1. Розбити наявні елементи масиву на пари і здійснити злиття елементів кожної пари, отримавши відсортовані ланцюжки довжини 2 (крім, можливо, одного елемента, для якого не знайшлося пари). Крок 2. Розбити наявні відсортовані ланцюжки на пари, і здійснити злиття ланцюжків кожної пари. Крок 3. Якщо число відсортованих ланцюжків більше одиниці, перейти до кроку 2. Недоліком алгоритму є те, що він вимагає додаткову пам'ять розміром порядку n (для зберігання допоміжного масиву). Крім того, він не гарантує збереження порядку елементів з однаковими значеннями.

Алгоритми сортування злиттям

Алгоритми сортування Короткі підсумки 1. Сортування є однією з фундаментальних алгоритмічних задач програмування. 2. Практично кожен алгоритм сортування можна розбити на 3 частини: порівняння, що визначає впорядкованість пари елементів; перестановку, який міняє місцями пару елементів; та власне алгоритм сортування, який здійснює порівняння і перестановку елементів до тих пір, поки всі елементи множини не будуть упорядковані. 3. Для оцінки трудомісткості алгоритмів сортування використовуються такі параметри: час сортування, додаткова пам'ять, стійкість і природність поведінки 4. За сферою застосування алгоритми сортувань класифікуються на алгоритми внутрішніх і зовнішніх сортувань. 5. Бінарне пірамідальне сортування є алгоритмом внутрішнього сортування, заснований на побудові піраміди та просіюванні елементів з її вершини методом спуску вниз у відповідності з ключем сортування 6. Пірамідальне сортування не використовує додаткової пам'яті. Метод не є стійким. Таке сортування на майже відсортованих масивах працює досить довго. 7. Сортування Шелла є алгоритмом внутрішнього сортування, заснований на порівнянні і переміщенні пар значень, розташованих спочатку досить далеко один від одного у наборі даних, з подальшим скороченням відстаней між ними.

Алгоритми сортування Короткі підсумки 8. Сортування Шелла є нестійким сортуванням за місцем. Ефективність методу Шелла пояснюється тим, що елементи, які зсовуються швидко потрапляють на потрібні місця. 9. Сортування Хоара є одним із різновидів швидких сортувань, заснованим на впорядкуванні підмножин масиву щодо опорних елементів. 10. Ефективність швидкого сортування в значній мірі визначається правильністю вибору опорних елементів при формуванні блоків. 11. Сортування злиттям є одним з найпростіших алгоритмів сортування серед швидких алгоритмів, який може бути ефективно використаний для сортування пов'язаних списків. 12. Недолік алгоритму сортування злиттям полягає в тому, що він вимагає додаткову пам'ять розміром порядку n, не гарантує збереження порядку елементів з однаковими значеннями. . 13. Швидке сортування є найбільш ефективним алгоритмом з усіх відомих методів сортування, але всі вдосконалені методи мають один спільний недолік - невисоку швидкість роботи при малих значеннях n.