e98bfeee28142500501d38a64aa03064.ppt
- Количество слайдов: 18

Algoritmi on-line e risoluzione di problemi complessi Carlo Fantozzi (carlo. fantozzi@dei. unipd. it)

Summary & Caveats • From Professor Ausiello’s course • Structure of the talk: w approximation algorithms (core) w on-line algorithms (a few words) • 16: 1 compression ratio! • Heterogeneous audience (& dumb speaker) • No details: only the framework of the course

Complexity Theory • What is efficiently computable? • Efficient = “Polynomial time” • Decision problems: yes/no answer • The P class: poly-time solution • The NP class: poly-time verification • Poly-time (Karp) reductions w NP-hard problems w NP-complete problems • P NP; is it also P=NP?

Optimization problems • Optimization problem: a quadruple w Set of instances I w Set of feasible solutions S w Cost function m(x, y), x I, y S w min/MAX • We are interested in optimal solutions • Example: min vertex cover

Optimization: 3 Approaches • Decision problem: “is there a solution with cost m? ” • Evaluation problem: “find optimal value of cost function” • Constructive optimization problem: “find the optimal solution” • Approaches are not (proved to be) equivalent. • They are equivalent whenever the decision problem is NP-complete.

Complexity Revised (1) • Solutions have polynomial size • Cost function computable in poly time • PO class: poly-time algorithm returns optimal solution and optimal cost • NPO class: poly-time verification alg. for feasible solutions • PO NPO; is it also PO=NPO?

Complexity Revised (2) • Poly-time Turing reductions; P 1 T P 2 if there exists an algorithm for P 1 which queries an oracle for P 2 • NP-hard optimization problem: every decision problem is T-reducible to it in poly time • PO=NPO if and only if P=NP: do not hope for poly-time algs…

Approximation Algs (1) • Poly-time algs that give approx solutions • Guaranteed performance (1970 s): maximum “distance” from optimum over all problem instances • Absolute approximation: cost within an additive constant from opt. • Relative error: E(x, y)=|opt(x)-m(x, y)|/MAX{opt(x), m(x, y)} • Performance ratio: R(x, y)=MAX{m(x, y)/opt(x), opt(x)/m(x, y)}

Approximation Algs (2) • r-approximate algorithm: R(x, y) r x, i. e. cost is at most r times the optimum • Example: min vertex cover (NP-hard) w Pick an edge w Include nodes of the edge into the cover w Remove nodes from the graph; repeat • Greedy algorithm is 2 -approximate

Approximation classes • Sometimes things are not so easy • Some problems are “more approximable” than others • Many approximation classes exist w The APX class w The PTAS class w The FPTAS class • These classes form a hierarchy if P NP

The APX class • Class of all NPO problems that admit a poly-time r-approximate algorithm • The general TSP is not in the APX class (unless P=NP) • The metric TSP is in the APX class (best algorithm: Cristofides', with a 3/2 performance ratio)

The PTAS class • Class of NPO problems that admit a poly-time approximation scheme • An approximaxion scheme is a tunable alg: can trade running time for performance • An algorithm is a PTAS for P if it gives an r-approx. solution in poly time for any r>1 • The metric TSP is not in the PTAS class: no (129/128)-approximate algorithm exists • The Euclidean TSP is in the PTAS class

The FPTAS class • The approximation scheme must be polynomial in both |x| and r • Problems in this class are optimally solvable for most practical purposes • The Euclidean TSP is not in FPTAS • Maximum Knapsack is in FPTAS • Not many problems belong to FPTAS
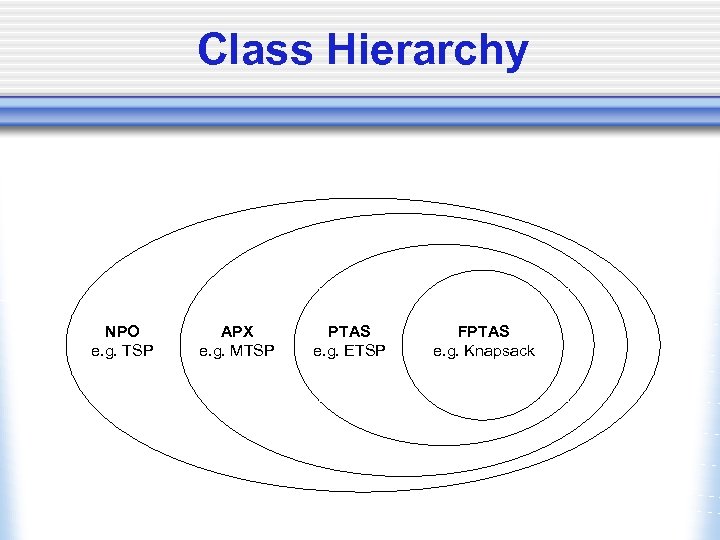
Class Hierarchy NPO e. g. TSP APX e. g. MTSP PTAS e. g. ETSP FPTAS e. g. Knapsack

Approximation Techniques • • • Greedy approach Linear programming Dynamic programming Randomization Computational geometry • A compendium of NPO problems: http: //www. nada. kth. se/~viggo/wwwcompendium/

On-Line Algorithms • An on-line algorithm w does not know entire input in advance w must take a decision each time it receives an input piece; each decision has a cost w total cost must be maximized/minimized • The constraint on the input makes these optimization problems much more difficult! • Off-line algorithm: knows entire input as usual

Performance Evaluation • Competitive analysis: compare on-line solution & optimal off-line sol. • On-line algorithm A is c-competitive if there exists a constant a such that m. A(x) cm. OPT(x)+a x • Worst-case analysis: A may perform much better on real-world inputs

Examples • Ski rental problem: for how long should a novice skier rent skis before buying? • Buy when the total cost of rental becomes higher than the cost of skis • Greedy strategy is 2 -competitive • Task scheduling problem • Graham’s algorithm (1966): assign new task to the less loaded processor • Greedy strategy is (2 -1/p)-competitive if the durations of tasks are known in advance
e98bfeee28142500501d38a64aa03064.ppt