Алгоритм Хаффмана алгоритм построения

•

Алгоритм Хаффмана – алгоритм построения кодов Хаффмана. Стратегии сжатия 1. Неадаптивная – используется заранее сформированная таблица кодов. 2. Полуадаптивная (блочная) Блок – конечная последовательность цифровой информации. Алгоритм получает на вход блок данных и формирует коды на основе статистических данных конкретного блока. 3. Адаптивная – коды формируются и корректируются во время кодирования.

Блочный алгоритм Хаффмана Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана. 1. Символы входного алфавита образуют список свободных узлов (листьев). Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение (удобнее рассматривать количество вхождений). 2. Выбираются два свободных узла дерева с наименьшими весами.

3. Создается их родитель с весом, равным их суммарному весу. 4. Родитель добавляется в список свободных узлов, а два его потомка удаляются из этого списка. 5. Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0. 6. Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева. Код символа есть последовательность нулей и единиц на ребрах на пути от корня дерева до листа, в котором лежит символ

• Узел и м п с Вес 4 1 1 3 Узел и мп с Вес 4 2 3

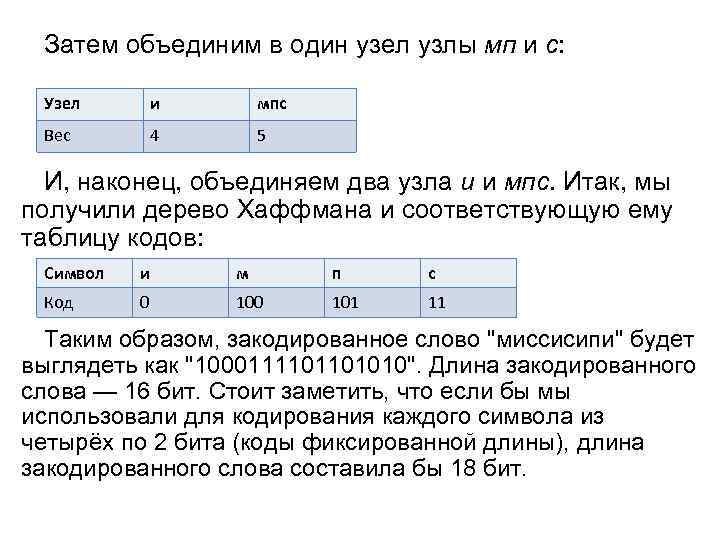Затем объединим в один узел узлы мп и c: Узел и мпс Вес 4 5 И, наконец, объединяем два узла и и мпс. Итак, мы получили дерево Хаффмана и соответствующую ему таблицу кодов: Символ и м п с Код 0 101 11 Таким образом, закодированное слово "миссисипи" будет выглядеть как "1000111101101010". Длина закодированного слова — 16 бит. Стоит заметить, что если бы мы использовали для кодирования каждого символа из четырёх по 2 бита (коды фиксированной длины), длина закодированного слова составила бы 18 бит.

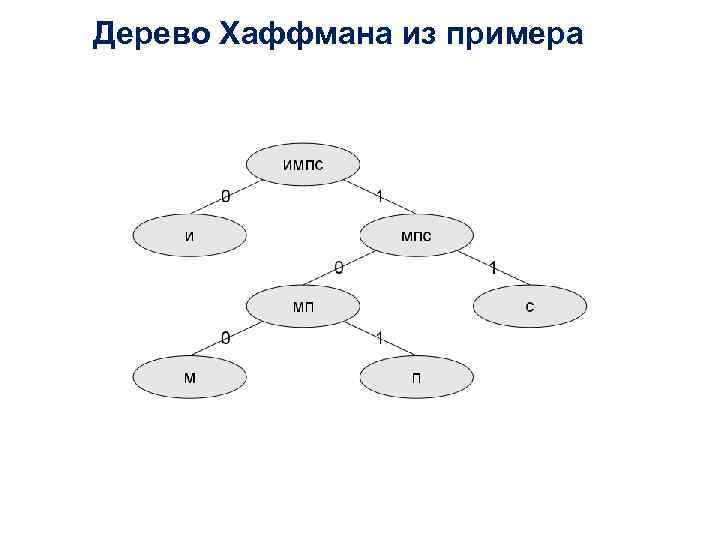Дерево Хаффмана из примера

Декодирование осуществляется следующим образом: на вход подается таблица вероятностей и, аналогично кодированию, строится дерево Хаффмана. Сделаем корень дерева текущей вершиной. Считывая символы (1 и 0) из закодированного файла, будем двигаться по соответствующим им ветвям. Придя в лист, получаем символ и возвращаемся в корень.

Недостатки блочного кодирования 1. Необходимость получать на вход весь блок сразу для сбора данных. 2. Необходимость два раза пробегать по блоку: первый раз для сбора данных, второй – для непосредственно кодирования. Для устранения этих недостатков используются адаптивные методы сжатия.

Адаптивный алгоритм Хаффмана Пусть в начале дерево имеет один лист - в нем лежит служебный символ, так называемый escapeсимвол. Построение дерева выполняется одновременно с кодированием. Символ, считанный первый раз, добавляется в лист. Каждый лист хранит счетчик вхождений символа. Каждый узел хранит сумму значений счетчиков всех его детей. Счетчик escape-символа равен нулю. Кодирование очередного символа в файле выглядит следующим образом: 1. Если символ встречается первый раз: • Выводим код escape-символа и несжатый код символа (обычно ASCII-код). Escape-символ служит для указания на то, что символ кодирован в несжатом виде.

• В дереве на место escape-символа вставляем новый узел, детьми которого делаем escape-символ и лист со считанным символом. 2. Если символ уже есть в дереве: • Выводим его код, равный последовательности нулей и единиц на ребрах на пути от листа, в котором лежит символ, до корня дерева. • Увеличиваем счетчик вхождений символа в листе. Соответственно, необходимо увеличить счетчик всех его предков до корня. Проверяем является ли полученное деревом Хаффмана и, при необходимости, выполняем модификацию дерева.

Проверка соблюдения свойств Назовем братьями две вершины, имеющие общего родителя в дереве. Дерево Хаффмана обладает так называемым свойством соперничества: Если расположить все вершины в дереве в виде списка, упорядоченного по неубыванию весов, то вершины-братья должны находиться рядом. Также свойство соперничества можно сформулировать следующим образом: Пусть вершины пронумерованы от корня к листьям и от левой вершины одной высоты к правой.

Тогда, если занести в список веса всех вершин в порядке их нумерации, то веса в списке должны быть упорядочены по невозрастанию. Если свойство соперничества нарушено, то коды символов в дереве не являются кодами Хаффмана. Модификация дерева Если после увеличения счетчика вершины, свойство соперничества нарушено, то его можно восстановить следующим образом: Пусть счетчик вершины равен N. 1. Находим вершину со счетчиком равным N-1 с минимальным номером (и не являющуюся предком текущей вершины). 2. Производим обмен поддеревьев текущей вершины и найденной.

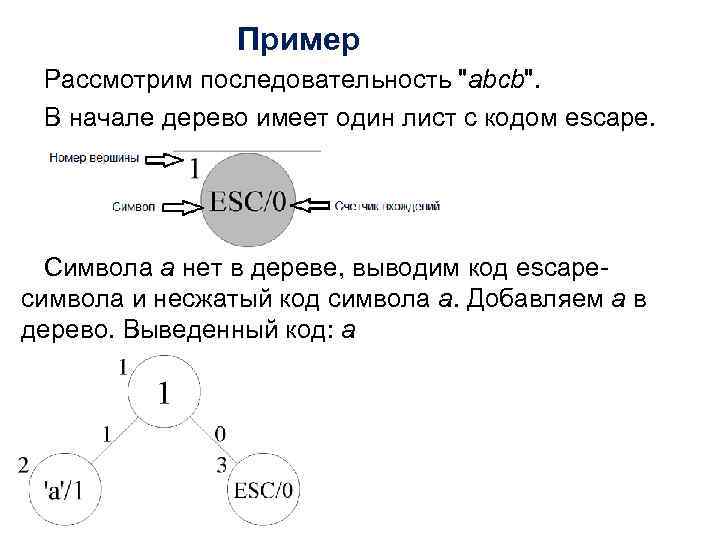Пример Рассмотрим последовательность "abcb". В начале дерево имеет один лист с кодом escape. Символа a нет в дереве, выводим код escapeсимвола и несжатый код символа a. Добавляем a в дерево. Выведенный код: a

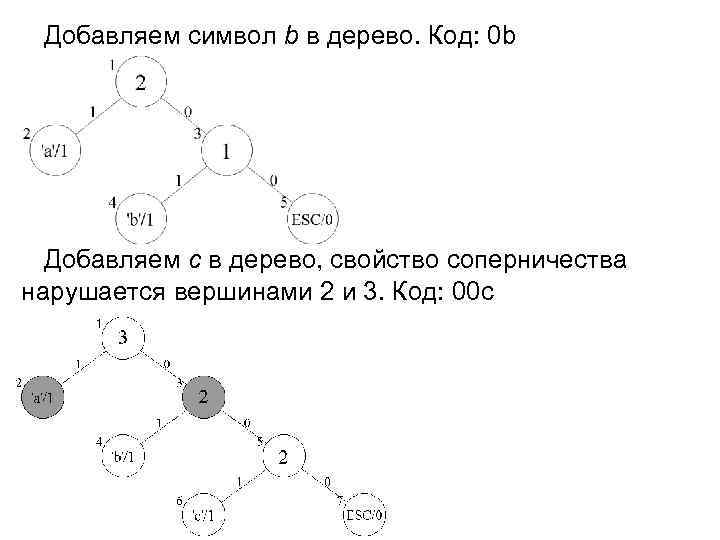Добавляем символ b в дерево. Код: 0 b Добавляем c в дерево, свойство соперничества нарушается вершинами 2 и 3. Код: 00 с

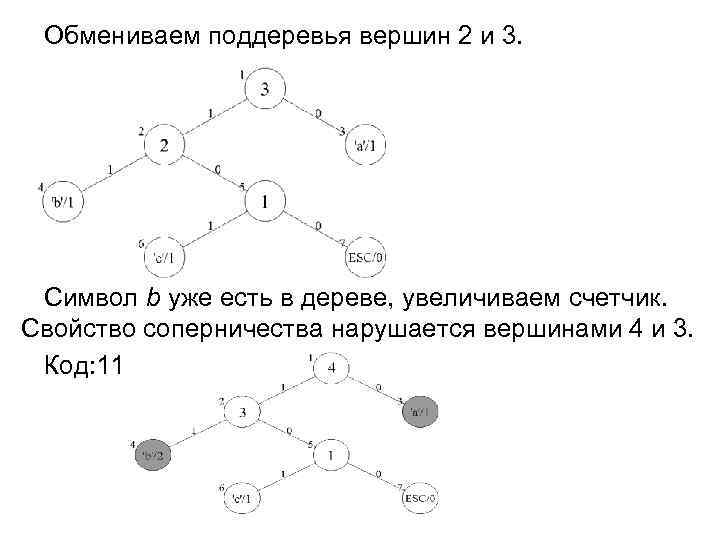Обмениваем поддеревья вершин 2 и 3. Символ b уже есть в дереве, увеличиваем счетчик. Свойство соперничества нарушается вершинами 4 и 3. Код: 11

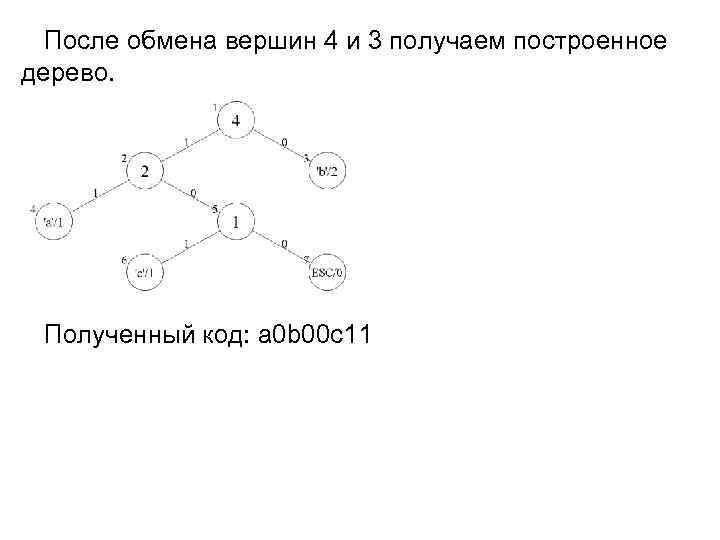После обмена вершин 4 и 3 получаем построенное дерево. Полученный код: a 0 b 00 с11

Декодирование производится симметрично кодированию: строится аналогичное кодовое дерево. Считываем последовательности кодов (0 и 1) из закодированного файла. Если приходим в escapeсимвол, то следующий код – код несжатого символа, добавляем его в дерево. Иначе, если приходим в любой другой символ, то увеличиваем его счетчик и выводим как декодированный.

Арифметическое кодирование Теоретически, обеспечивает наилучшее сжатие среди статистических методов. Практическая реализация сопряжена с рядом трудностей. Классический метод арифметического кодирования является полуадаптивным, то есть алгоритм получает на вход таблицу вероятностей символов. Пpи аpифметическом кодиpовании данные пpедставляются вещественными числами в интеpвале от 0 до 1. По меpе кодиpования данных, интеpвал уменьшается, а количество битов для его пpедставления возpастает. Чем больше вероятность символа, тем меньше уменьшается интервал. Таким образом, для кодирования более вероятных символов требуется меньше битов.

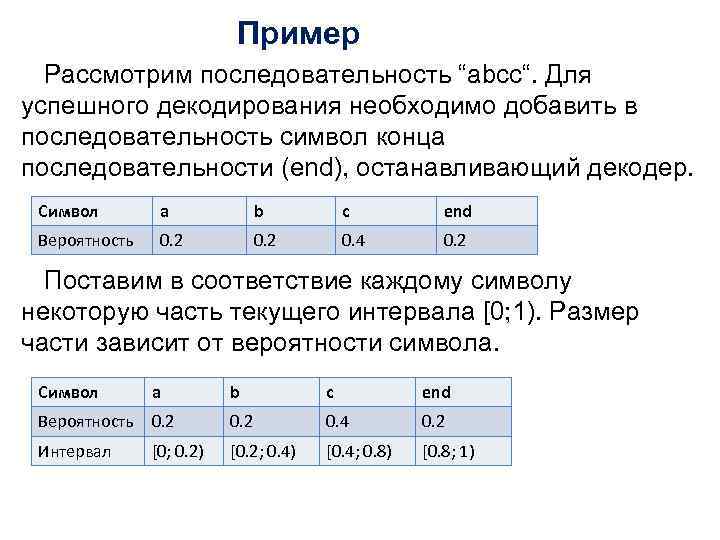Пример Рассмотрим последовательность “abcc“. Для успешного декодирования необходимо добавить в последовательность символ конца последовательности (end), останавливающий декодер. Символ a b c end Вероятность 0. 2 0. 4 0. 2 Поставим в соответствие каждому символу некоторую часть текущего интервала [0; 1). Размер части зависит от вероятности символа. Символ a b c end Вероятность 0. 2 0. 4 0. 2 Интервал [0; 0. 2) [0. 2; 0. 4) [0. 4; 0. 8) [0. 8; 1)

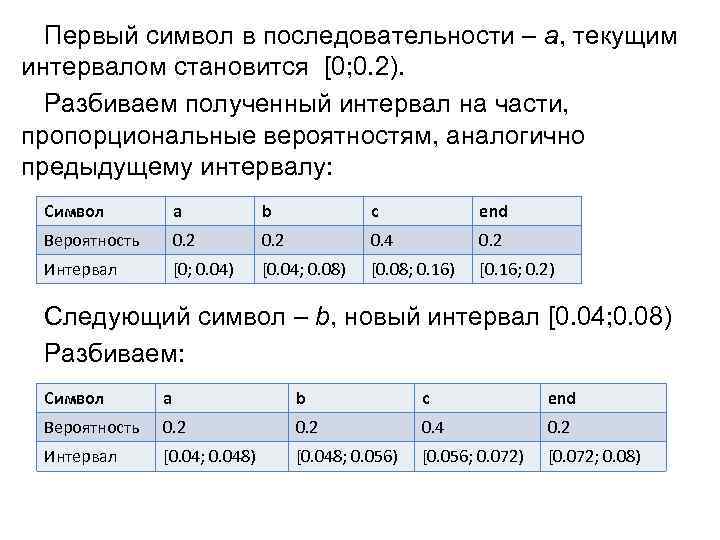Первый символ в последовательности – a, текущим интервалом становится [0; 0. 2). Разбиваем полученный интервал на части, пропорциональные вероятностям, аналогично предыдущему интервалу: Символ a b c end Вероятность 0. 2 0. 4 0. 2 Интервал [0; 0. 04) [0. 04; 0. 08) [0. 08; 0. 16) [0. 16; 0. 2) Следующий символ – b, новый интервал [0. 04; 0. 08) Разбиваем: Символ a b c end Вероятность 0. 2 0. 4 0. 2 Интервал [0. 04; 0. 048) [0. 048; 0. 056) [0. 056; 0. 072) [0. 072; 0. 08)

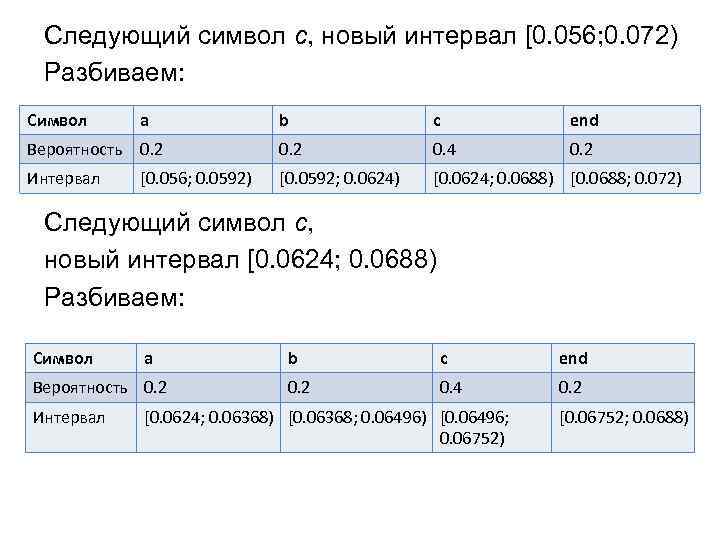Следующий символ c, новый интервал [0. 056; 0. 072) Разбиваем: Символ a b c end Вероятность 0. 2 0. 4 0. 2 Интервал [0. 056; 0. 0592) [0. 0592; 0. 0624) [0. 0624; 0. 0688) [0. 0688; 0. 072) Следующий символ c, новый интервал [0. 0624; 0. 0688) Разбиваем: Символ a Вероятность 0. 2 Интервал b c end 0. 2 0. 4 0. 2 [0. 0624; 0. 06368) [0. 06368; 0. 06496) [0. 06496; 0. 06752) [0. 06752; 0. 0688)

Следующий символ end. Итоговый интервал [0. 06752; 0. 0688) Результатом кодирования является любое число из итогового интервала. С помощью него и начальной таблицы вероятностей можно восстановить входную последовательность символов. Из интервала в примере можно взять число 0. 068, итого мы храним три цифры (068) вместо четырех букв. Т. к. арифметика чисел с плавающей точкой недостаточно точна, то границы интервала хранятся в целых числах. Закодированный файл состоит из длинного целого числа, принадлежащего итоговому интервалу.

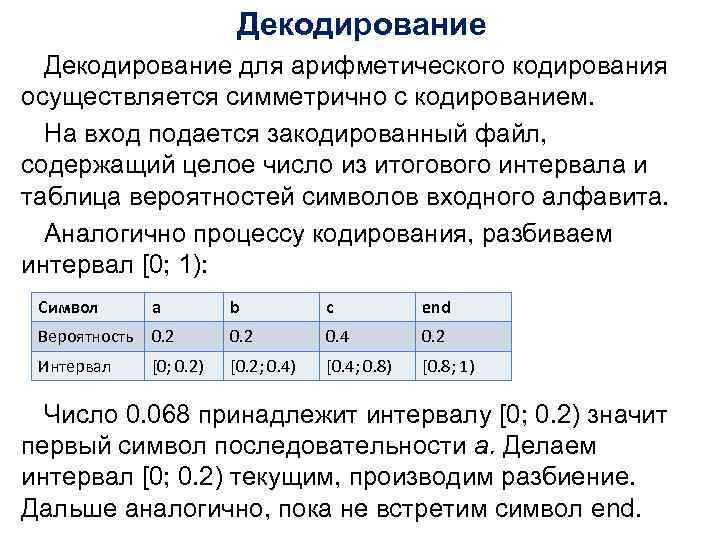Декодирование для арифметического кодирования осуществляется симметрично с кодированием. На вход подается закодированный файл, содержащий целое число из итогового интервала и таблица вероятностей символов входного алфавита. Аналогично процессу кодирования, разбиваем интервал [0; 1): Символ a b c end Вероятность 0. 2 0. 4 0. 2 Интервал [0; 0. 2) [0. 2; 0. 4) [0. 4; 0. 8) [0. 8; 1) Число 0. 068 принадлежит интервалу [0; 0. 2) значит первый символ последовательности a. Делаем интервал [0; 0. 2) текущим, производим разбиение. Дальше аналогично, пока не встретим символ end.