Алгоритм расчета 1 определяют ряд условных величин

Алгоритм расчета • 1. определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и последующих факторов, допуская, что остальные не меняются.

• 2. Сравниваются величины результативного показателя до и после изменения уровня того или другого фактора, что позволяет элиминировать влияние всех факторов, и определить воздействие последнего на прирост результативного показателя.

Пример. Объем валового выпуска продукции (ВП) зависит от двух основных факторов первого порядка: численности рабочих (ЧР) и среднегодовой выработки (ГВ). Имеем двухфакторную модель: ВП = ЧР • ГВ.

• Таблица 1 Данные для факторного анализа валового выпуска продукции

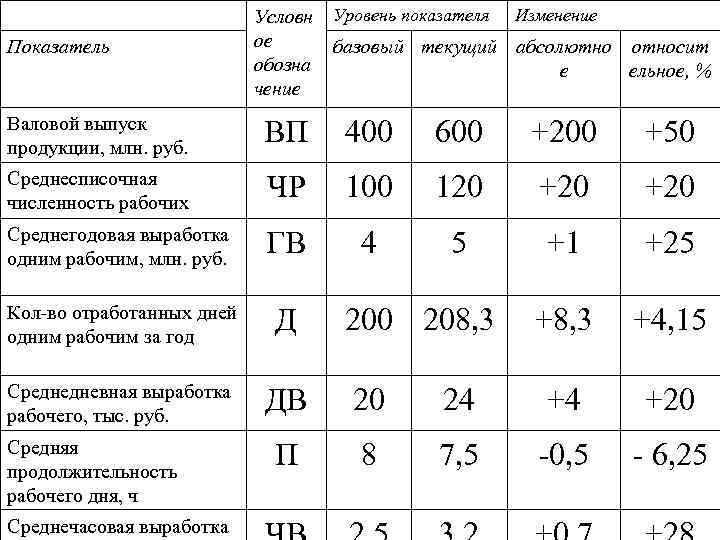Показатель Условн ое обозна чение Уровень показателя Изменение базовый текущий абсолютно относит е ельное, % Валовой выпуск продукции, млн. руб. ВП 400 600 +200 +50 Среднесписочная численность рабочих ЧР 100 120 +20 Среднегодовая выработка одним рабочим, млн. руб. ГВ 4 5 +1 +25 Кол-во отработанных дней одним рабочим за год Д +8, 3 +4, 15 Среднедневная выработка рабочего, тыс. руб. ДВ 20 24 +4 +20 П 8 7, 5 -0, 5 - 6, 25 Средняя продолжительность рабочего дня, ч Среднечасовая выработка 200 208, 3

Алгоритм расчета способом цепной подстановки для этой модели: • ВП 0= ЧР 0 • ГВ 0 = 100 • 4 = 400 млн. руб. ; • ВП усл. = ЧР 1 • ГВ 0 = 120 • 4 = 480 млн. руб. ; • ВП 1 = ЧР 1 • ГВ 1 = 120 • 5 = 600 млн. руб.

Таким образом, увеличение выпуска продукции вызвано следующими факторами: • а) рост численности рабочих(ЧР) + 80 млн. руб. ; • б) рост уровня произв. труда(ГВ) +120 млн. руб. • Итого + 200 млн. руб. Алгебраич. сумма влияния факторов должна быть равна общему приросту результативного показателя: ∆ВПчр + ∆ВПгв = ∆ВПобщ.

четырехфакторная модель выпуска продукции: • ВП = ЧР • Д • П • ЧВ

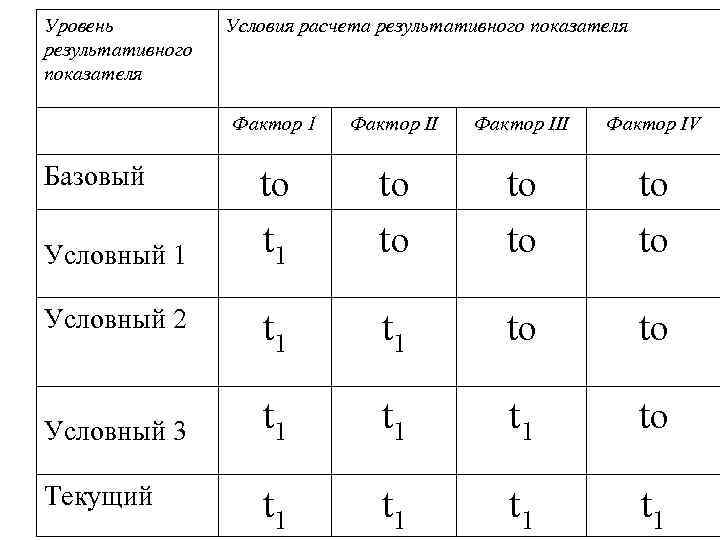Уровень результативного показателя Условия расчета результативного показателя Фактор 1 Фактор III Фактор IV to t 1 to to to Условный 2 t 1 to to Условный 3 t 1 t 1 to Текущий t 1 t 1 Базовый Условный 1

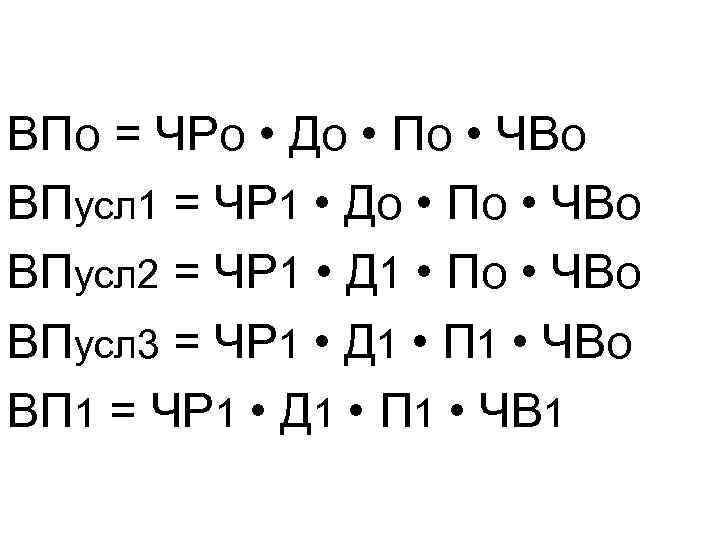ВПо = ЧРо • До • По • ЧВо ВПусл 1 = ЧР 1 • До • По • ЧВо ВПусл 2 = ЧР 1 • Д 1 • По • ЧВо ВПусл 3 = ЧР 1 • Д 1 • П 1 • ЧВо ВП 1 = ЧР 1 • Д 1 • П 1 • ЧВ 1

Объем выпуска продукции в целом вырос на 200 млн. руб. (600 — 400), в том числе за счет изменения: а) количества рабочих ∆ВПчр = ВПусл 1 - ВП 0 б) количества отработанных дней одним рабочим за год ∆ВПд = ВПусл 2 - ВПусл 1 = 500 - 480 в) средней продолжительности рабочего дня ∆ВПП= ВПусл 3 - ВПусл 2 г)среднечасовой выработки ∆ВПчв=ВП 1 - ВПусл 3

Алгоритм расчетов по методу цепной подстановки : • В первую очередь нужно учитывать изменение количественных, а затем качественных показателей.

• Если же имеется несколько количественных и несколько качественных показателей, то сначала изменяют величину факторов первого уровня подчинения, а потом более низкого.

применяется для расчета влияния факторов на прирост результативного показателя только в мультипликативных моделях Y = x 1 • x 2 • х3 • • • хп и моделях мультипликативно-аддитивного типа: Y = (а — b) с и Y = а (b — с).

• При этом величина влияния факторов рассчитывается умножением абсолютного прироста значения исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.

• Алгоритм расчета для мультипликативной четырехфакторной модели валового выпуска продукции выглядит следующим образом: ВП = ЧР • Д • П • ЧВ.

• ∆ВПчр = ∆ЧР • До • По • ЧВ 0 • ∆ВПД = ЧР 1 • ∆Д • П 0 • ЧВ 0 • ∆ВПП = ЧР 1 • Д 1 • ∆П • ЧВ 0 • ∆ВПЧВ = ЧР 1 • Д 1 • П 1 • ∆ЧВ

• Алгоритм расчета факторов способом абсолютных разниц в моделях мультипликативно-аддитивного вида. Используем факторную модель прибыли от реализации продукции: П = VРП(Ц-С), где П — прибыль от реализации продукции; VРП — объем реализации продукции; Ц — цена единицы продукции; С — себестоимость единицы продукции.

Прирост суммы прибыли за счет изменения: • объема реализации продукции ∆Пvрп = ∆VРП (Цо — Со); • цены реализации ∆ПЦ = VРП 1 • ∆Ц; • себестоимости продукции ∆ПС = VРП 1 (– ∆С).

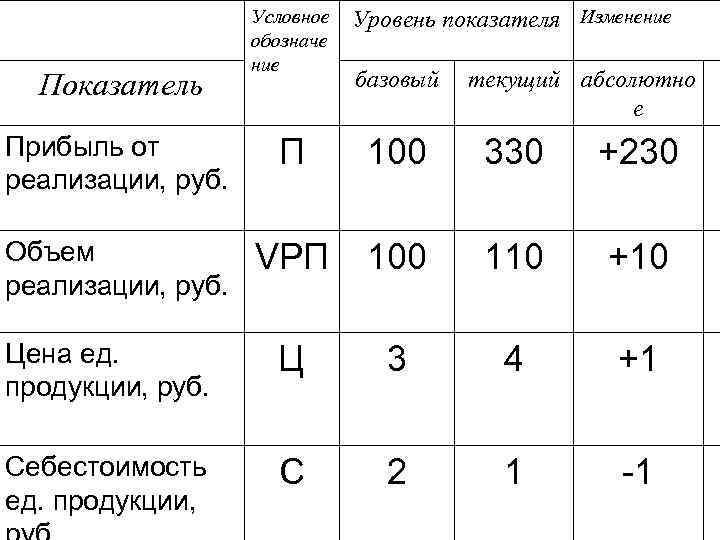Показатель Условное обозначе ние Уровень показателя Изменение базовый текущий абсолютно е Прибыль от реализации, руб. П 100 330 +230 Объем реализации, руб. VРП 100 110 +10 Цена ед. продукции, руб. Ц 3 4 +1 Себестоимость ед. продукции, С 2 1 -1

применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных моделях Y = abc. Здесь используются относительные приросты факторных показателей, выраженные в виде коэффициентов или процентов.

Алгоритм определения изменения результативного показателя

• для расчета влияния первого фактора необходимо базовую величину результативного показателя умножить на отношение абсолютного прироста первого фактора к его базисному значению.

• Для расчета влияния второго фактора, к базовой величине результативного показателя прибавляют изменение его за счет первого фактора и полученную сумму умножают на относительный прирост второго фактора.

• для определения влияния третьего фактора к базовой величине результативного показателя прибавляют его прирост за счет первого и второго факторов и полученную сумму умножают на относительный прирост третьего фактора и т. д.

• Закрепим рассмотренную методику на примере, приведенном в табл. 1: На ВП влияли трудовые факторы: ЧР (ср списочная численность рабочих), Д (кол-во отработанных 1 рабочих дней), П (ср. продолжительность рабочего дня), ЧВ (ср. часовая выработка 1 рабочего)

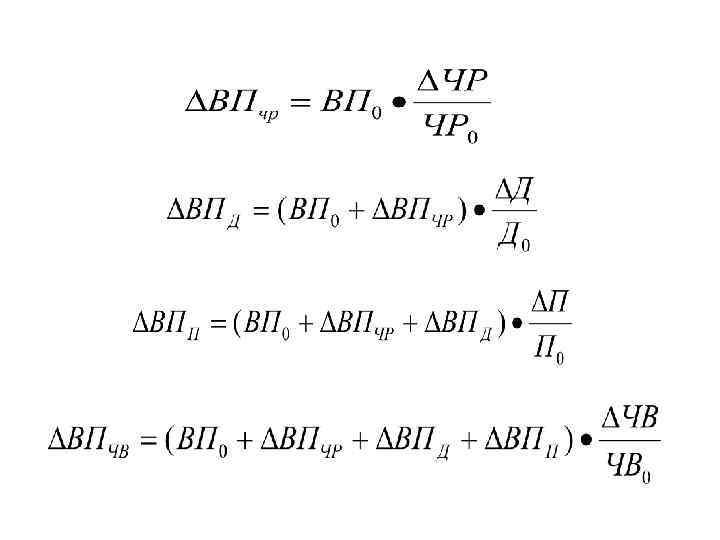
расчет

• Способ относительных разниц эффективен когда надо рассчитать влияние значительного числа факторов (более 10). В отличие от предыдущих способов здесь значительно сокращается число вычислений. В этом его главное преимущество.

Способ пропорционального деления применяется в случаях, когда мы имеем дело с : аддитивными моделями Y= a + b + с

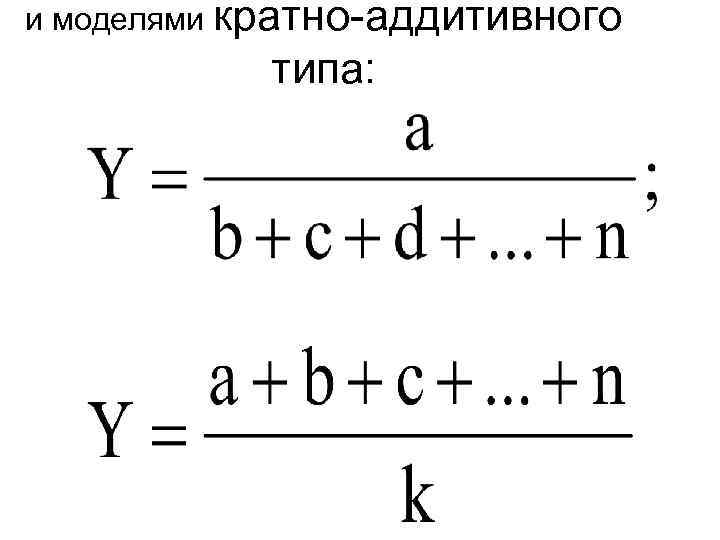и моделями кратно-аддитивного типа:

В первом случае, когда имеем одноуровневую модель типа Y= a + b + с, расчет проводится следующим образом:

• В моделях кратно-аддитивного типа сначала способом цепной подстановки определяют насколько изменился результативный показатель за счет числителя и знаменателя, а затем рассчитывают влияние факторов второго порядка способом пропорционального

Пример. Имеются данные: уровень рентабельности повысился на 8% в связи с увеличением суммы прибыли на 1000 тыс. руб. При этом прибыль возросла за счет увеличения объема продаж на 500 тыс. руб. , за счет роста цен — на 1700 тыс. руб. , а за счет роста себестоимости продукции снизилась на 1200 тыс. руб.

Определим, как изменился уровень рентабельности за счет каждого фактора:

• Для решения подобного типа задач используют также способ долевого участия. При этом сначала определяется доля каждого фактора в общей сумме их приростов по формулам:

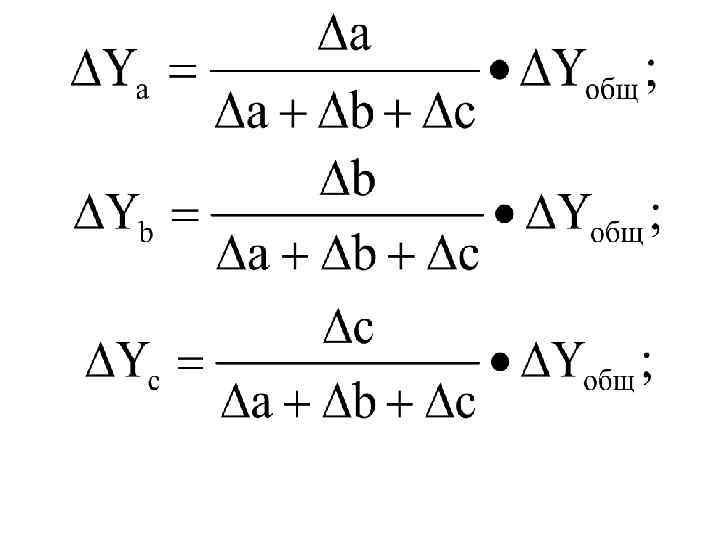
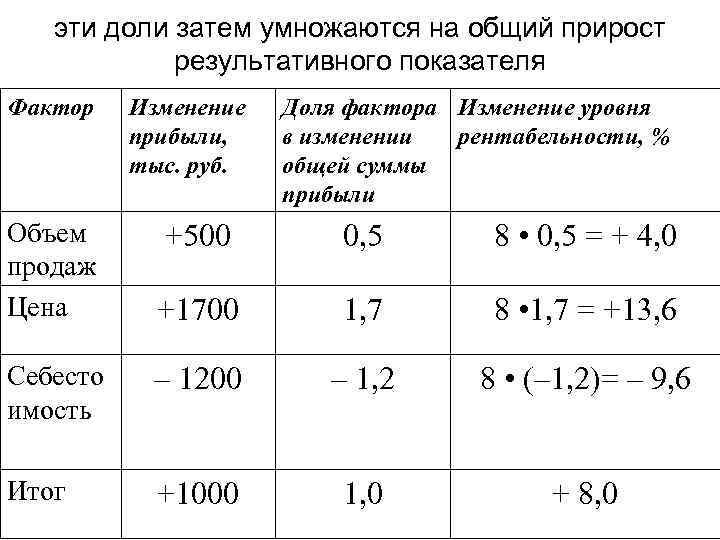эти доли затем умножаются на общий прирост результативного показателя Фактор Объем продаж Цена Изменение прибыли, тыс. руб. Доля фактора Изменение уровня в изменении рентабельности, % общей суммы прибыли +500 0, 5 8 • 0, 5 = + 4, 0 +1700 1, 7 8 • 1, 7 = +13, 6 Себесто имость – 1200 – 1, 2 8 • (– 1, 2)= – 9, 6 Итог +1000 1, 0 + 8, 0

применяется в мультипликативных, кратных и кратно-аддитивных моделях. Дает более точный результат расчета влияния факторов, т. к. дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними. Кроме того, результат расчета не зависит от месторасположения

Алгоритмы расчетов влияния факторов для разных моделей:

Пример ( табл. 1) расчет влияния факторов : • ВП = ЧР • ГВ. ∆ВПчр = (+20) • 4 + 1/2 (20 • 1) = + 90 тыс. руб. ; ∆ВПгв = (+1) • 100+ 1/2 (20 • 1) = + 110 тыс. руб.

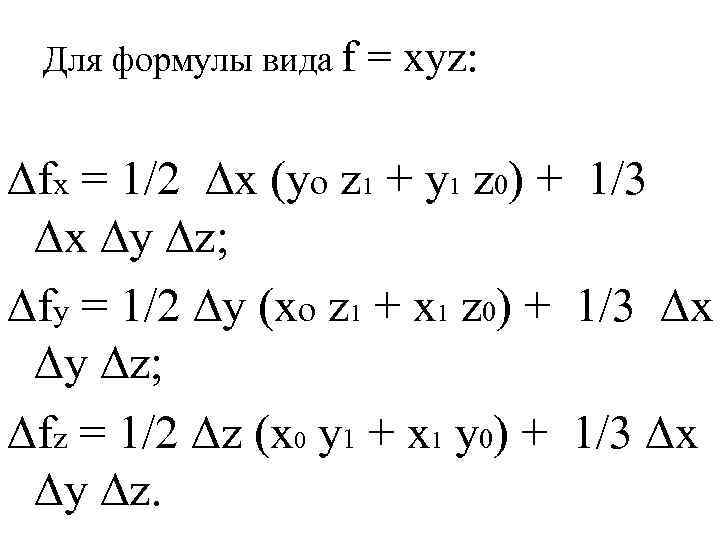Для формулы вида f = xyz: ∆fx = 1/2 ∆х (yo z 1 + y 1 z 0) + 1/3 ∆х ∆у ∆z; ∆fy = 1/2 ∆y (xo z 1 + x 1 z 0) + 1/3 ∆х ∆y ∆z; ∆fz = 1/2 ∆z (x 0 y 1 + x 1 y 0) + 1/3 ∆x ∆y ∆z.

Пример ( табл. 1) расчета влияния факторов : • ВП = ЧР • ДВ. ∆ВПчр = 1/2 • 20 • (200 • 24 + 208, 33 • 20) + 1/3 • 20 • 8, 33 • 4 = +89 890; ∆ВПД = 1/2 • 8, 33 • (100 • 24 + 120 • 20) + 1/3 • 20 • 8, 33 • 4 = +20 222; ∆ВПДВ = 1/2 • 4 (100 • 208, 33 + 120 • 200) + 1/3 • 20 • 8, 33 • 4 = +89 888;

Для расчета влияния факторов в кратных и смешанных моделях используются следующие формулы: • 1. Вид факторной модели

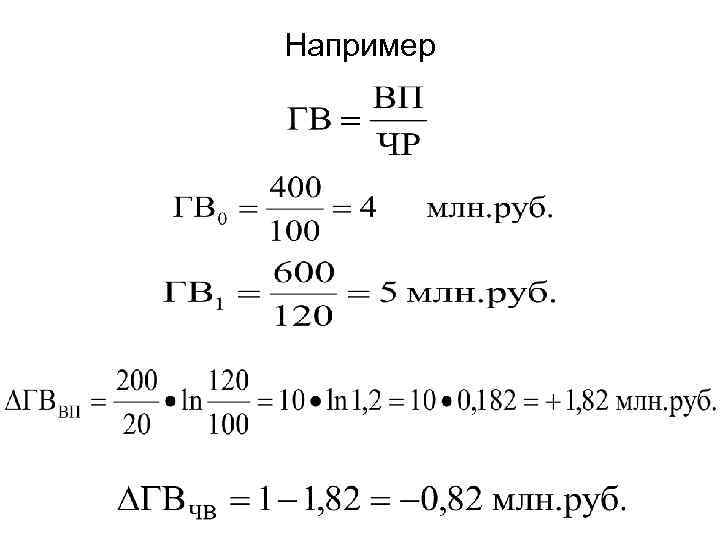Например

2. Вид факторной модели

• Если в знаменателе больше двух факторов, то процедура продолжается. Таким образом, использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в эти готовые рабочие формулы подставить необходимые числовые данные. Результат расчета также не зависит от месторасположения факторов в модели.

применяется для измерения влияния факторов в мультипликативных моделях. Как и при интегрировании, здесь результат расчета не зависит от месторасположения факторов в модели. По сравнению с интегральным методом логарифмирование обеспечивает большую точность расчетов.

• Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доле изолированного влияния каждого фактора на уровень результативного показателя. В этом его преимущество, а недостаток — в ограниченности сферы применения.

• В отличие от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их роста (снижения). Представим результативный показатель в виде произведения трех факторов: f = xyz.

Влияние факторов определяется по формулам:

• Из формул следует, что общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму индекса результативного показателя. И не имеет значения, какой логарифм используется — натуральный или десятичный.

• Пример (см. табл. 1) определим прирост выпуска продукции за счет изменения численности рабочих (ЧР), количества отработанных дней одним рабочим за год (Д) и среднедневной выработки (ДВ) по факторной модели: ВП = ЧР

• Преимущество способа логарифмирования состоит в относительной простоте вычислений и более высокой точности расчетов. Сферу применения приемов детерминированного факторного анализа в систематизированном виде можно представить в виде следующей матрицы.

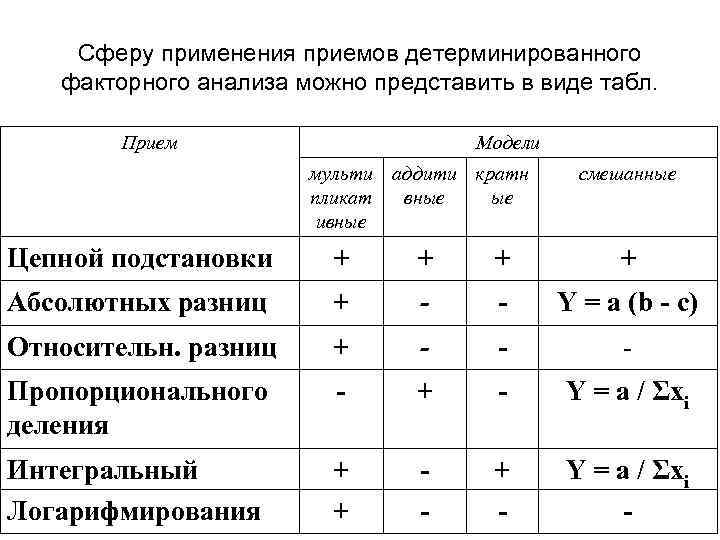Сферу применения приемов детерминированного факторного анализа можно представить в виде табл. Прием Модели мульти аддити кратн пликат вные ые ивные смешанные Цепной подстановки + + Абсолютных разниц + - - Y = а (b - с) Относительн. разниц + - - - Пропорционального деления - + - Y = a / Σxi Интегральный Логарифмирования + + - Y = a / Σxi -