Алгоритм нахождения расстояния от источника до всех вершин

Алгоритм нахождения расстояния от источника до всех вершин — метод Форда — Беллмана n Данные: Ориентированный граф V, E с n вершинами n 1 2 3 4 5 6 с выделенным источником s V, матрица дуг A[u, v], u, v V (граф не содержит контуров отрицательной длины). Результаты: Расстояния от источника до всех вершин графа: D[v]=d(s, v), v V. begin for v V do D [v] : = A[s, v]; D [s] : = 0; for k : = 1 to n – 2 do for v V {s} do for u V do D [v] : = min(D[v], D[u] + A [u, v]) end

Случай неотрицательных весов — алгоритм Дейкстры n Пусть (V, E) — нагруженный граф, и s — его вершина. n Алгоритм выбирает кратчайший путь от вершины s до любой вершины v и присваивает его длину переменной d[v]. n В списке Path. To(v) перечисляются вершины кратчайшего пути от s к v.

n n n n n Begin For каждой do Begin d[v] : =A(s, v) Path. To(v): =s end Отметить вершину s; While есть неотмеченные вершины do Begin u: =неотмеченную вершину с мин. расст. от s; отметить вершину u; for каждой неотмеченной вершины v с условием uv E do begin d’ : = d[u] + A(u, v) ; If d’ < d[v] then begin d[v] : = d’ ; Path. To(v): =Path. To(u), v; end End; End

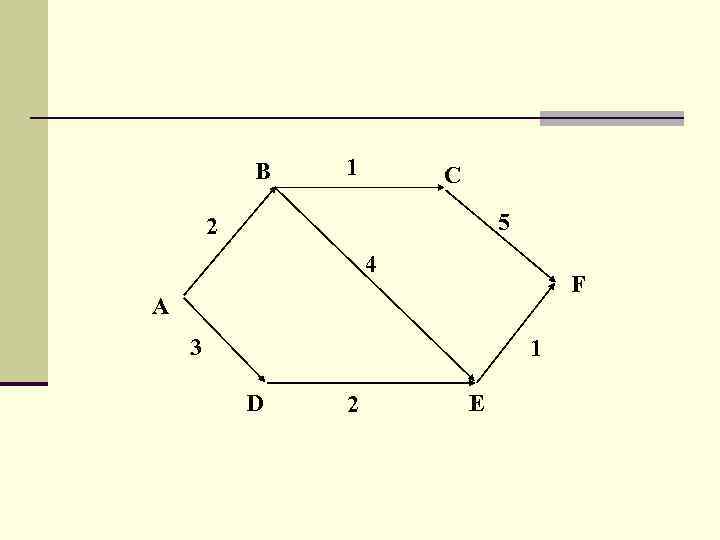B 1 C 5 2 4 F A 3 1 D 2 E

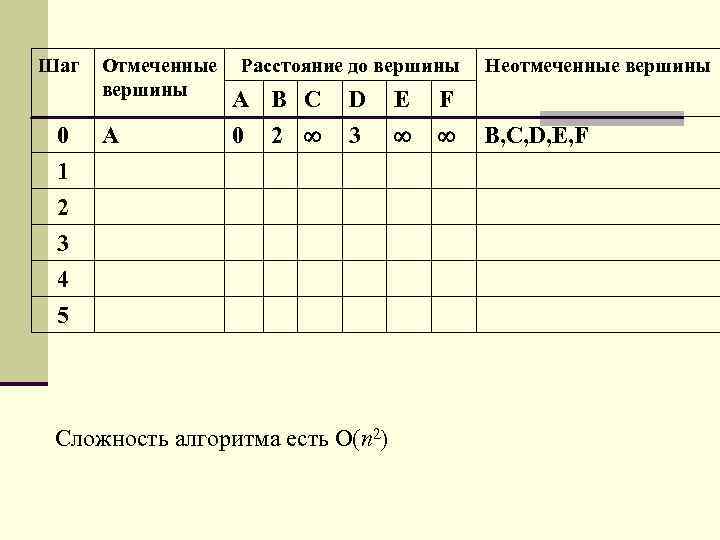Шаг 0 Отмеченные вершины A Расстояние до вершины A B C D E F 2 3 Неотмеченные вершины 0 1 2 3 4 5 Сложность алгоритма есть O(n 2) B, C, D, E, F