Рекурсия и сложность алгоритмов.ppt
- Количество слайдов: 69
 Алгоритм –это конечная последовательность указаний на языке понятном исполнителю, задающая процесс решения задач определенного типа и ведущая к получению результата, однозначно определяемого допустимыми исходными данными. 1
Алгоритм –это конечная последовательность указаний на языке понятном исполнителю, задающая процесс решения задач определенного типа и ведущая к получению результата, однозначно определяемого допустимыми исходными данными. 1
 Алгоритмические машины (АМ) имеют единственный процессор, выполняющий небольшой набор очень примитивных действий, простую структуру данных (структуру памяти) в виде бесконечной ленты, простую логику (правила) управления процессором. 2
Алгоритмические машины (АМ) имеют единственный процессор, выполняющий небольшой набор очень примитивных действий, простую структуру данных (структуру памяти) в виде бесконечной ленты, простую логику (правила) управления процессором. 2
 Основные АМ Машина Тьюринга (МТ) предложена Тьюрингом в 1937 г. Машина Тьюринга (МТ) предложена Тьюрингом в 1937 г. Машина Поста (МР) предложена Постом в 1937 г. Нормальный алгоритм Маркова (НАМ) предложен Марковым в 1953 г. 3
Основные АМ Машина Тьюринга (МТ) предложена Тьюрингом в 1937 г. Машина Тьюринга (МТ) предложена Тьюрингом в 1937 г. Машина Поста (МР) предложена Постом в 1937 г. Нормальный алгоритм Маркова (НАМ) предложен Марковым в 1953 г. 3
 Функции вычислимые алгоритмом алгоритм не определяется формально, а существует как бы в виде «всем понятной механической процедуры» . алгоритм не определяется формально, а существует как бы в виде «всем понятной механической процедуры» . Любая функция, вычислимая на интуитивном (содержательном) уровне, должна быть сконструирована из базовых. 4
Функции вычислимые алгоритмом алгоритм не определяется формально, а существует как бы в виде «всем понятной механической процедуры» . алгоритм не определяется формально, а существует как бы в виде «всем понятной механической процедуры» . Любая функция, вычислимая на интуитивном (содержательном) уровне, должна быть сконструирована из базовых. 4
 Рекурсивные функции на множестве натуральных чисел были предложены Клини в 1938 г. Конструктивные механизмы рекурсивных функций очень просты, их применение в процессе построения «функции от функции» позволяет явно выстраивать структуру функции в отличие от АМ, где функция определяется процедурно, через последовательность действий. 5
Рекурсивные функции на множестве натуральных чисел были предложены Клини в 1938 г. Конструктивные механизмы рекурсивных функций очень просты, их применение в процессе построения «функции от функции» позволяет явно выстраивать структуру функции в отличие от АМ, где функция определяется процедурно, через последовательность действий. 5
 Исчисления Исчисление функций, вычисляемых на множестве натуральных чисел предложено Эрбраном и Гёделем в 1938 г. -исчисление А. Чёрча также может быть отнесено к этому типу алгоритмов, предложено в 1937 г. Формальные грамматики, порождающие языки, предложены Хомским в 1953 – 1956 г. Формальные грамматики, порождающие языки, предложены Хомским в 1953 – 1956 г. 6
Исчисления Исчисление функций, вычисляемых на множестве натуральных чисел предложено Эрбраном и Гёделем в 1938 г. -исчисление А. Чёрча также может быть отнесено к этому типу алгоритмов, предложено в 1937 г. Формальные грамматики, порождающие языки, предложены Хомским в 1953 – 1956 г. Формальные грамматики, порождающие языки, предложены Хомским в 1953 – 1956 г. 6
 Структура алгоритма (составляющие алгоритма) Процессорная структура. (Исполнитель алгоритма). Во всех теоретических конструкциях алгоритмов и большинстве алгоритмических языках это единственный процессор. Структуры данных. Структура данных это способ организация записи, хранения и извлечение данных. Данные – это элементы множеств, которые нужно порождать или распознавать. . 7
Структура алгоритма (составляющие алгоритма) Процессорная структура. (Исполнитель алгоритма). Во всех теоретических конструкциях алгоритмов и большинстве алгоритмических языках это единственный процессор. Структуры данных. Структура данных это способ организация записи, хранения и извлечение данных. Данные – это элементы множеств, которые нужно порождать или распознавать. . 7
 Машина Тьюринга (МТ) Машина Тьюринга - это универсальная учебная машина, созданная для уточнения понятия алгоритм. Первым из всех ученых идею универсального исполнителя предложил Алан Тьюринг (1936 г. ). Для уточнения понятия алгоритма, им был разработан абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель. Например, операции, которые выполняют реальные вычислительные машины можно имитировать на универсальном исполнителе. В последствие, придуманная Тьюрингом вычислительная конструкция была названа машиной Тьюринга. 8
Машина Тьюринга (МТ) Машина Тьюринга - это универсальная учебная машина, созданная для уточнения понятия алгоритм. Первым из всех ученых идею универсального исполнителя предложил Алан Тьюринг (1936 г. ). Для уточнения понятия алгоритма, им был разработан абстрактный универсальный исполнитель. Его абстрактность заключается в том, что он представляет собой логическую вычислительную конструкцию, а не реальную вычислительную машину. Термин «универсальный исполнитель» говорит о том, что данный исполнитель может имитировать любой другой исполнитель. Например, операции, которые выполняют реальные вычислительные машины можно имитировать на универсальном исполнителе. В последствие, придуманная Тьюрингом вычислительная конструкция была названа машиной Тьюринга. 8
 Интерпретация МТ Процессор – в МТ называется управляющей головкой (УГ). Структура данных (память процессора) бесконечная лента, разбитая на ячейки, в ячейку может быть записан только один символ Процесс вычислений происходит по тактам. Процесс остановки (остановка) МТ. Замечание: Список правил для МТ не упорядочен Замечание Список правил для МТ не упорядочен 9
Интерпретация МТ Процессор – в МТ называется управляющей головкой (УГ). Структура данных (память процессора) бесконечная лента, разбитая на ячейки, в ячейку может быть записан только один символ Процесс вычислений происходит по тактам. Процесс остановки (остановка) МТ. Замечание: Список правил для МТ не упорядочен Замечание Список правил для МТ не упорядочен 9
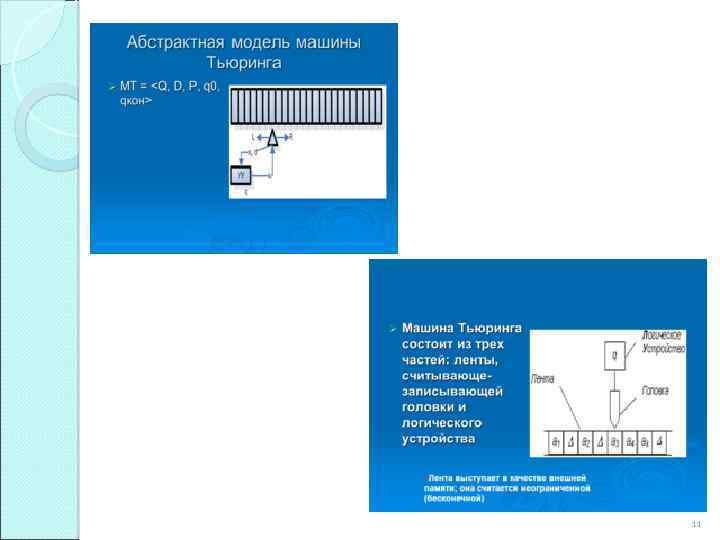
 Структура машины Тьюринга Машина Тьюринга состоит из: - бесконечной в обе стороны ленты, разделенной на ячейки; - каретки (читающей и записывающей головки); - программируемого автомата. Программируемый автомат управляет кареткой, посылая ей команды в соответствии с заложенной в него сменяемой программой. Лента выполняет роль внешней памяти компьютера, автомат — роль процессора, а каретка служит для ввода и вывода данных. 10
Структура машины Тьюринга Машина Тьюринга состоит из: - бесконечной в обе стороны ленты, разделенной на ячейки; - каретки (читающей и записывающей головки); - программируемого автомата. Программируемый автомат управляет кареткой, посылая ей команды в соответствии с заложенной в него сменяемой программой. Лента выполняет роль внешней памяти компьютера, автомат — роль процессора, а каретка служит для ввода и вывода данных. 10
 11
11
 Программа для машины Тьюринга Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице. Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие: Внешний алфавит. Конечное множество (обозначают буквой А), элементы которого называются буквами (символами). Одна из букв этого алфавита (например, а 0) должна представлять собой пустой символ. Например, алфавит машины Тьюринга, работающей с двоичными числами, задается в виде A = {0, 1, а 0}. Непрерывную цепочку символов на ленте называют словом.
Программа для машины Тьюринга Программы для машин Тьюринга записываются в виде таблицы, где первые столбец и строка содержат буквы внешнего алфавита и возможные внутренние состояния автомата (внутренний алфавит). Содержимое таблицы представляет собой команды для машины Тьюринга. Буква, которую считывает головка в ячейке (над которой она находится в данный момент), и внутренне состояние головки определяют, какую команду нужно выполнить. Команда определяется пересечением символов внешнего и внутреннего алфавитов в таблице. Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие: Внешний алфавит. Конечное множество (обозначают буквой А), элементы которого называются буквами (символами). Одна из букв этого алфавита (например, а 0) должна представлять собой пустой символ. Например, алфавит машины Тьюринга, работающей с двоичными числами, задается в виде A = {0, 1, а 0}. Непрерывную цепочку символов на ленте называют словом.
 Автоматом называют устройство, работающее без участия человека. Автомат в машине Тьюринга имеет несколько состояний и при определенных условиях переходит из одного состояния в другое. Множество состояний автомата называют внутренним алфавитом. Внутренний алфавит. Конечное множество состояний каретки (автомата). Обозначается буквой Q={q 1, q 2. . . }. Одно из состояний - q 1 - должно быть начальным (запускающим программу). Еще одно из состояний (q 0) должно быть конечным (завершающим программу) – состояние остановка. Таблица переходов. Описание поведения автомата (каретки) в зависимости от состояния и считанного символа. 13
Автоматом называют устройство, работающее без участия человека. Автомат в машине Тьюринга имеет несколько состояний и при определенных условиях переходит из одного состояния в другое. Множество состояний автомата называют внутренним алфавитом. Внутренний алфавит. Конечное множество состояний каретки (автомата). Обозначается буквой Q={q 1, q 2. . . }. Одно из состояний - q 1 - должно быть начальным (запускающим программу). Еще одно из состояний (q 0) должно быть конечным (завершающим программу) – состояние остановка. Таблица переходов. Описание поведения автомата (каретки) в зависимости от состояния и считанного символа. 13
 Автомат машины Тьюринга в процессе своей работы управляется программой, во время каждого шага которой выполняются последовательно следующие действия: - Записывать символ внешнего алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой). - Передвигаться на одну ячейку влево или вправо. - Менять свое внутреннее состояние. Поэтому при составлении программы для каждой пары (символ, состояние) нужно определить три параметра: символ ai из выбранного алфавита A, направление перемещения каретки ("←” — влево, "→” — вправо, "точка” — нет перемещения) и новое состояние автомата qk. Например, команда 1 "←” q 2 обозначает "заменить символ на 1, переместить каретку влево на одну ячейку и перейти в состояние q 2”. 14
Автомат машины Тьюринга в процессе своей работы управляется программой, во время каждого шага которой выполняются последовательно следующие действия: - Записывать символ внешнего алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой). - Передвигаться на одну ячейку влево или вправо. - Менять свое внутреннее состояние. Поэтому при составлении программы для каждой пары (символ, состояние) нужно определить три параметра: символ ai из выбранного алфавита A, направление перемещения каретки ("←” — влево, "→” — вправо, "точка” — нет перемещения) и новое состояние автомата qk. Например, команда 1 "←” q 2 обозначает "заменить символ на 1, переместить каретку влево на одну ячейку и перейти в состояние q 2”. 14
 Предполагается, что универсальный исполнитель должен уметь доказывать существование или отсутствие алгоритма для той или иной задачи. Тезис Чёрча-Тьюринга: Любой алгоритм может быть представлен как программа для машины Тьюринга. Алгоритм - это программа для машины Тьюринга Т. о. можно дать формальное определение алгоритма по Тьюрингу. Машина Тьюринга - математический объект, и данное на ее основе определение алгоритма может использоваться для доказательства. 15
Предполагается, что универсальный исполнитель должен уметь доказывать существование или отсутствие алгоритма для той или иной задачи. Тезис Чёрча-Тьюринга: Любой алгоритм может быть представлен как программа для машины Тьюринга. Алгоритм - это программа для машины Тьюринга Т. о. можно дать формальное определение алгоритма по Тьюрингу. Машина Тьюринга - математический объект, и данное на ее основе определение алгоритма может использоваться для доказательства. 15
 Примеры работы машины Тьюринга Задача 1. На ленте записано число в двоичной системе счисления. Каретка находится где-то над числом. Требуется увеличить число на единицу. Чтобы решить задачу, нам нужно: -определить алфавит машины Тьюринга А, - определить набор состояний Q, - составить программу (т. е. для каждой пары (аi, qi) определить команду автомата. ) Алфавит машины Тьюринга, работающей с двоичными цифрами будет включать цифры 0, 1 и пробел a 0. Т. е. А={1, 0, a 0}. Определим возможные состояния: 1. q 1 - автомат ищет правый конец слова (числа) на ленте 2. q 2 - автомат увеличивает число на 1, проходя его слева направо и останавливается, закончив работу. Напишем программу: 1 часть. q 1 - автомат ищет правый конец слова (числа на ленте) 1)если в рабочей ячейке записано 0 - переместиться вправо 2)если в рабочей ячейке записано 1 - переместиться вправо 3) если в рабочей ячейке пробел, переместить каретку влево и перейти в состояние q 2 16
Примеры работы машины Тьюринга Задача 1. На ленте записано число в двоичной системе счисления. Каретка находится где-то над числом. Требуется увеличить число на единицу. Чтобы решить задачу, нам нужно: -определить алфавит машины Тьюринга А, - определить набор состояний Q, - составить программу (т. е. для каждой пары (аi, qi) определить команду автомата. ) Алфавит машины Тьюринга, работающей с двоичными цифрами будет включать цифры 0, 1 и пробел a 0. Т. е. А={1, 0, a 0}. Определим возможные состояния: 1. q 1 - автомат ищет правый конец слова (числа) на ленте 2. q 2 - автомат увеличивает число на 1, проходя его слева направо и останавливается, закончив работу. Напишем программу: 1 часть. q 1 - автомат ищет правый конец слова (числа на ленте) 1)если в рабочей ячейке записано 0 - переместиться вправо 2)если в рабочей ячейке записано 1 - переместиться вправо 3) если в рабочей ячейке пробел, переместить каретку влево и перейти в состояние q 2 16
 Составим таблицу переходов для q 1 т. о. : q 2 - автомат увеличивает число на 1, проходя его слева направо и останавливается, закончив работу. 1) если в рабочей ячейке записана цифра 0, записать в нее 1 и стоп 2) если в рабочей ячейке записана цифра 1, выполнить перенос в старший разряд — записать в ячейку 0 и переместиться влево. 3) если в рабочей ячейке пробел, записать в нее 1 и стоп. Добавим в нашу таблицу состояние q 2: Построенная таблица и есть программа для машины Тьюринга. 17
Составим таблицу переходов для q 1 т. о. : q 2 - автомат увеличивает число на 1, проходя его слева направо и останавливается, закончив работу. 1) если в рабочей ячейке записана цифра 0, записать в нее 1 и стоп 2) если в рабочей ячейке записана цифра 1, выполнить перенос в старший разряд — записать в ячейку 0 и переместиться влево. 3) если в рабочей ячейке пробел, записать в нее 1 и стоп. Добавим в нашу таблицу состояние q 2: Построенная таблица и есть программа для машины Тьюринга. 17
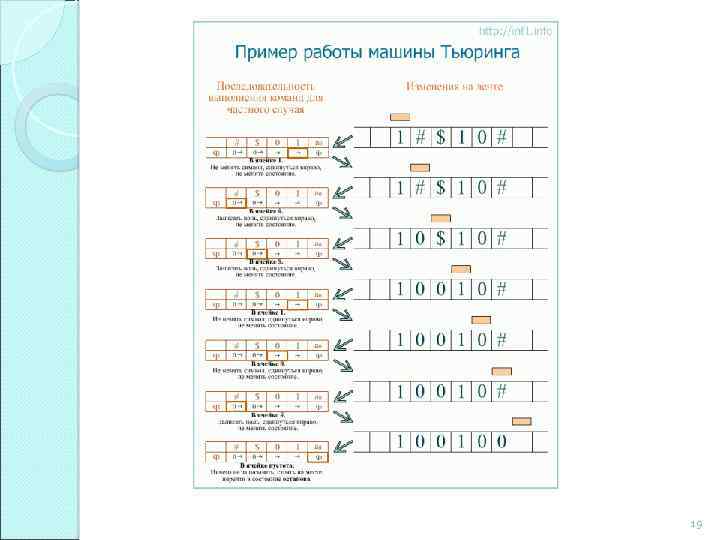
 Задача 2. Допустим, на ленте есть слово, состоящее из символов #, $, 1 и 0. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над первой буквой слова слева. Завершается программа тогда, когда головка оказывается над пустым символом после самой правой буквы слова. Примечание: длина слова и последовательность символов значения не имеют. На рисунке приводится пример последовательности выполнения команд для конкретного случая. Если на ленте будет другое слово, то и последовательность выполнения команд будет другой. Несмотря на это, данная программа для машины Тьюринга (на рисунке – таблица слева) применима к любым словам описанного внешнего алфавита (соблюдается свойство применимости алгоритма ко всем однотипным задачам – массовость). 18
Задача 2. Допустим, на ленте есть слово, состоящее из символов #, $, 1 и 0. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над первой буквой слова слева. Завершается программа тогда, когда головка оказывается над пустым символом после самой правой буквы слова. Примечание: длина слова и последовательность символов значения не имеют. На рисунке приводится пример последовательности выполнения команд для конкретного случая. Если на ленте будет другое слово, то и последовательность выполнения команд будет другой. Несмотря на это, данная программа для машины Тьюринга (на рисунке – таблица слева) применима к любым словам описанного внешнего алфавита (соблюдается свойство применимости алгоритма ко всем однотипным задачам – массовость). 18
 19
19
 Задача 3. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над любой буквой слова. ВОПРОСЫ: 1. Что такое машина Тьюринга? 2. Сопоставьте устройство машины Тьюринга с устройством компьютера. Какие устройства машины Тьюринга выполняют те же функции, что и аналогичные устройства компьютера? 3. Сформулируйте тезис Чёрча — Тьюринга. Литература: 1. Майер Р. В. Машины Поста и Тьюринга (komp-model. narod. ru) 2. Пильщиков В. Н. , Абрамов В. Г. , Вылиток А. А. , Горячая И. В. Машины Тьюринга и алгоритмы Маркова. Решение задач. М. : МГУ, 2006. 20
Задача 3. Требуется заменить все символы # и $ на нули. В момент запуска головка находится над любой буквой слова. ВОПРОСЫ: 1. Что такое машина Тьюринга? 2. Сопоставьте устройство машины Тьюринга с устройством компьютера. Какие устройства машины Тьюринга выполняют те же функции, что и аналогичные устройства компьютера? 3. Сформулируйте тезис Чёрча — Тьюринга. Литература: 1. Майер Р. В. Машины Поста и Тьюринга (komp-model. narod. ru) 2. Пильщиков В. Н. , Абрамов В. Г. , Вылиток А. А. , Горячая И. В. Машины Тьюринга и алгоритмы Маркова. Решение задач. М. : МГУ, 2006. 20
 Рекурсия и ее реализация Рекурсия реализуется на основе подпрограммы, вызывающей саму себя. Первый вызов рекурсивной подпрограммы выполняется из внешней программы. Типы рекурсии: - прямая (функция содержит вызов самой себя); - косвенная (функция F 1 вызывает функцию F 2, которая вызывает исходную F 1) 21
Рекурсия и ее реализация Рекурсия реализуется на основе подпрограммы, вызывающей саму себя. Первый вызов рекурсивной подпрограммы выполняется из внешней программы. Типы рекурсии: - прямая (функция содержит вызов самой себя); - косвенная (функция F 1 вызывает функцию F 2, которая вызывает исходную F 1) 21
 Этапы разработки рекурсивного алгоритма решения задачи 1) параметризация задачи, т. е. выявление различных элементов, от которых зависит ее решение, с целью нахождения управляющего параметра. При этом размерность управляющего параметра должна убывать после каждого рекурсивного вызова по мере нахождения решения; 2) поиск тривиального случая и его решения. На этом этапе должно быть найдено решение задачи без рекурсии; 3) декомпозиция общего случая, требующая привести его к одной или нескольким более простым задачам меньшей размерности. 2 2
Этапы разработки рекурсивного алгоритма решения задачи 1) параметризация задачи, т. е. выявление различных элементов, от которых зависит ее решение, с целью нахождения управляющего параметра. При этом размерность управляющего параметра должна убывать после каждого рекурсивного вызова по мере нахождения решения; 2) поиск тривиального случая и его решения. На этом этапе должно быть найдено решение задачи без рекурсии; 3) декомпозиция общего случая, требующая привести его к одной или нескольким более простым задачам меньшей размерности. 2 2
 Рекурсивный алгоритм вычисления факториала Формула факториала: n! =n*(n – 1)*(n – 2)*. . . *1 управляющий параметр -текущее значение числа n. Тривиальный случай представляет собой 0! = 1 декомпозиция общего случая n! = n*(n – 1)! 23
Рекурсивный алгоритм вычисления факториала Формула факториала: n! =n*(n – 1)*(n – 2)*. . . *1 управляющий параметр -текущее значение числа n. Тривиальный случай представляет собой 0! = 1 декомпозиция общего случая n! = n*(n – 1)! 23
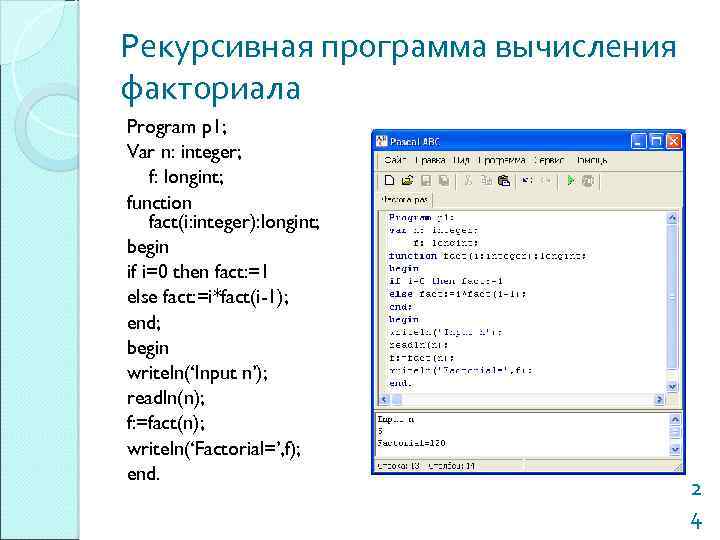 Рекурсивная программа вычисления факториала Program p 1; Var n: integer; f: longint; function fact(i: integer): longint; begin if i=0 then fact: =1 else fact: =i*fact(i-1); end; begin writeln(‘Input n’); readln(n); f: =fact(n); writeln(‘Factorial=’, f); end. 2 4
Рекурсивная программа вычисления факториала Program p 1; Var n: integer; f: longint; function fact(i: integer): longint; begin if i=0 then fact: =1 else fact: =i*fact(i-1); end; begin writeln(‘Input n’); readln(n); f: =fact(n); writeln(‘Factorial=’, f); end. 2 4
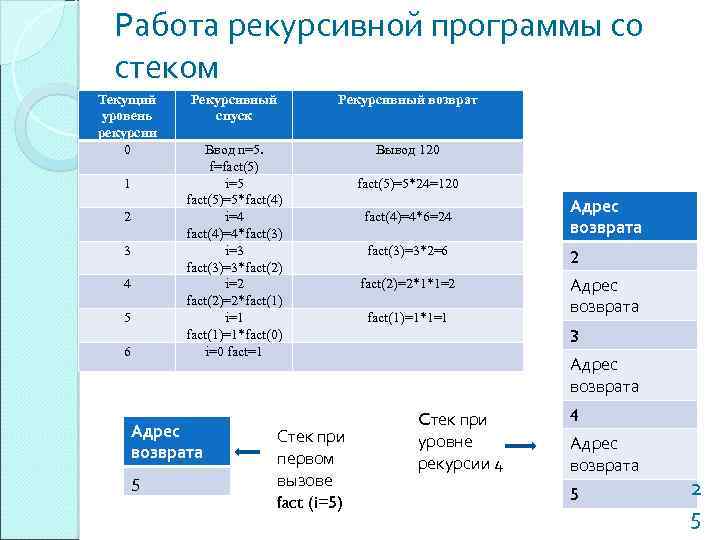 Работа рекурсивной программы со стеком Текущий уровень рекурсии 0 1 2 3 4 5 6 Рекурсивный спуск Рекурсивный возврат Ввод n=5. f=fact(5) i=5 fact(5)=5*fact(4) i=4 fact(4)=4*fact(3) i=3 fact(3)=3*fact(2) i=2 fact(2)=2*fact(1) i=1 fact(1)=1*fact(0) i=0 fact=1 Вывод 120 Адрес возврата 5 Стек при первом вызове fact (i=5) fact(5)=5*24=120 fact(4)=4*6=24 Адрес возврата fact(3)=3*2=6 2 fact(2)=2*1*1=2 fact(1)=1*1=1 Адрес возврата 3 Адрес возврата Cтек при уровне рекурсии 4 4 Адрес возврата 5 2 5
Работа рекурсивной программы со стеком Текущий уровень рекурсии 0 1 2 3 4 5 6 Рекурсивный спуск Рекурсивный возврат Ввод n=5. f=fact(5) i=5 fact(5)=5*fact(4) i=4 fact(4)=4*fact(3) i=3 fact(3)=3*fact(2) i=2 fact(2)=2*fact(1) i=1 fact(1)=1*fact(0) i=0 fact=1 Вывод 120 Адрес возврата 5 Стек при первом вызове fact (i=5) fact(5)=5*24=120 fact(4)=4*6=24 Адрес возврата fact(3)=3*2=6 2 fact(2)=2*1*1=2 fact(1)=1*1=1 Адрес возврата 3 Адрес возврата Cтек при уровне рекурсии 4 4 Адрес возврата 5 2 5
 Роль стека при вызове подпрограммы В из А 1. В вершину стека помещается фрагмент нужного размера. В него входят следующие данные: (а) указатели фактических параметров при вызове процедуры В; (б) пустые ячейки для локальных переменных, определенных в процедуре В; (в) адрес возврата, т. е. адрес команды в процедуре А, которую следует выполнить после того, как процедура В закончит свою работу. Если В - функция, то во фрагмент стека для В помещается указатель ячейки во фрагменте стека для А, в которую надлежит поместить значение этой функции (адрес значения). 2. Управление передается первому оператору процедуры В. 3. При завершении работы процедуры В управление передается процедуре А с помощью следующей последовательности шагов: (а) адрес возврата извлекается из вершины стека (б) если В функция, то ее значение запоминается в ячейке, предписанной указателем на адрес значения; (в) фрагмент стека процедуры В извлекается из стека, в вершину ставится фрагмент процедуры А; (г) выполнение процедуры А возобновляется с команды, указанной в адресе возврата. При вызове подпрограммой самой себя, т. е. в рекурсивном случае, выполняется 2 та же самая последовательность действий. 6
Роль стека при вызове подпрограммы В из А 1. В вершину стека помещается фрагмент нужного размера. В него входят следующие данные: (а) указатели фактических параметров при вызове процедуры В; (б) пустые ячейки для локальных переменных, определенных в процедуре В; (в) адрес возврата, т. е. адрес команды в процедуре А, которую следует выполнить после того, как процедура В закончит свою работу. Если В - функция, то во фрагмент стека для В помещается указатель ячейки во фрагменте стека для А, в которую надлежит поместить значение этой функции (адрес значения). 2. Управление передается первому оператору процедуры В. 3. При завершении работы процедуры В управление передается процедуре А с помощью следующей последовательности шагов: (а) адрес возврата извлекается из вершины стека (б) если В функция, то ее значение запоминается в ячейке, предписанной указателем на адрес значения; (в) фрагмент стека процедуры В извлекается из стека, в вершину ставится фрагмент процедуры А; (г) выполнение процедуры А возобновляется с команды, указанной в адресе возврата. При вызове подпрограммой самой себя, т. е. в рекурсивном случае, выполняется 2 та же самая последовательность действий. 6
 Рекурсивное вычисление чисел Фибоначчи F(1)=1, F(2)=1, для любого n>2 F(n)=F(n-1)+F(n-2) Program p 2; var n: integer; ch: longint; function fib(i: Integer): Longint; Begin if (i=1) or (i=2) then fib: =1 else fib: =fib(i-1)+fib(i-2); end; begin writeln('Input n'); readln(n); ch: =fib(n); writeln('Fib. with number=', n, ‘ is ', ch); end. 27
Рекурсивное вычисление чисел Фибоначчи F(1)=1, F(2)=1, для любого n>2 F(n)=F(n-1)+F(n-2) Program p 2; var n: integer; ch: longint; function fib(i: Integer): Longint; Begin if (i=1) or (i=2) then fib: =1 else fib: =fib(i-1)+fib(i-2); end; begin writeln('Input n'); readln(n); ch: =fib(n); writeln('Fib. with number=', n, ‘ is ', ch); end. 27
 Задача «Ханойские башни» Существует легенда: «В храме Бендареса находится бронзовая плита с тремя алмазными стержнями. На один из стержней бог при сотворении мира нанизал 64 диска разного диаметра из чистого золота. Наибольший диск лежит на бронзовой плите и с остальными образует пирамиду, сужающуюся кверху. Это – башня Брамы. Работая день и ночь, жрецы переносят диски с одного стержня на другой, следуя законам Брамы: 1) диски можно перемещать с одного стержня на другой только по одному; 2) нельзя класть больший диск на меньший; 3)при переносе дисков с одного стержня на другой можно использовать промежуточный третий стержень, на котором диски тоже могут находиться тоже только в виде пирамиды. 2 Когда все 64 диска будут перенесены с одного стержня на другой, наступит конец света» . 8
Задача «Ханойские башни» Существует легенда: «В храме Бендареса находится бронзовая плита с тремя алмазными стержнями. На один из стержней бог при сотворении мира нанизал 64 диска разного диаметра из чистого золота. Наибольший диск лежит на бронзовой плите и с остальными образует пирамиду, сужающуюся кверху. Это – башня Брамы. Работая день и ночь, жрецы переносят диски с одного стержня на другой, следуя законам Брамы: 1) диски можно перемещать с одного стержня на другой только по одному; 2) нельзя класть больший диск на меньший; 3)при переносе дисков с одного стержня на другой можно использовать промежуточный третий стержень, на котором диски тоже могут находиться тоже только в виде пирамиды. 2 Когда все 64 диска будут перенесены с одного стержня на другой, наступит конец света» . 8
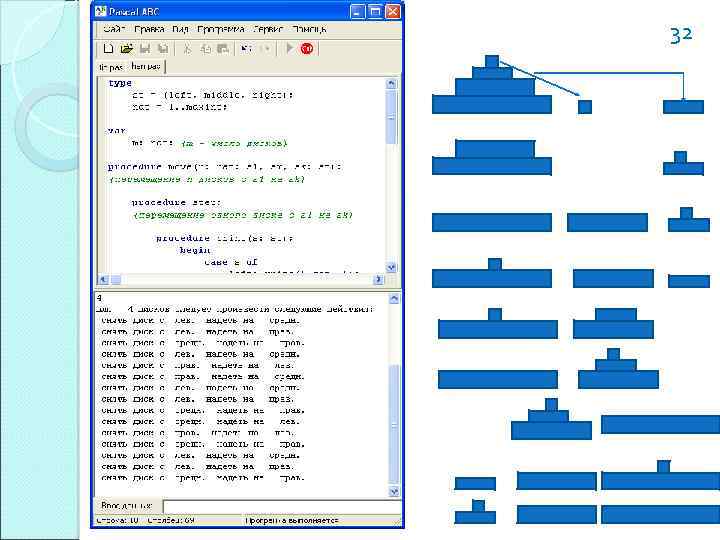
 Алгоритм решения задачи «Ханойские башни» Назовем стержни левым (left), средним (middle) и правым (right). Задача состоит в переносе m дисков с левого стержня на правый. Задача может быть решена одним перемещением только для одного (m = 1) диска. Построим рекурсивное решение задачи, состоящее из трех этапов: a) перенести башню, состоящую из m – 1 диска, с левого стержня на средний; b) перенести один оставшийся диск с левого стержня на правый; c) перенести башню, состоящую из m – 1 диска, со среднего стержня на правый. 29
Алгоритм решения задачи «Ханойские башни» Назовем стержни левым (left), средним (middle) и правым (right). Задача состоит в переносе m дисков с левого стержня на правый. Задача может быть решена одним перемещением только для одного (m = 1) диска. Построим рекурсивное решение задачи, состоящее из трех этапов: a) перенести башню, состоящую из m – 1 диска, с левого стержня на средний; b) перенести один оставшийся диск с левого стержня на правый; c) перенести башню, состоящую из m – 1 диска, со среднего стержня на правый. 29
 Программа «Ханойские башни» : обозначения Обозначим тот стержень, с которого следует снять диски, через s 1, на который надеть – через sk, а вспомогательный стержень через sw. Оформим алгоритм решения задачи о переносе башни из n дисков с s 1 на sk в виде процедуры move с 4 -мя параметрами: n, s 1, sw, sk; алгоритм для n = 1 выделим в отдельную процедуру step, которая перемещает один диск со стержня s 1 на sk. 30
Программа «Ханойские башни» : обозначения Обозначим тот стержень, с которого следует снять диски, через s 1, на который надеть – через sk, а вспомогательный стержень через sw. Оформим алгоритм решения задачи о переносе башни из n дисков с s 1 на sk в виде процедуры move с 4 -мя параметрами: n, s 1, sw, sk; алгоритм для n = 1 выделим в отдельную процедуру step, которая перемещает один диск со стержня s 1 на sk. 30
 Type st = (left, middle, right); nat = 1. . maxint; var m: nat; {m – число дисков} procedure move(n: nat; s 1, sw, sk: st); {перемещение n дисков с s 1 на sk} procedure step; {перемещение одного диска с s 1 на sk} procedure print(s: st); begin case s of left: write(' лев. '); middle: write(' средн. '); right: write(' прав. ') end; begin {step} write(' снять диск с '); print(s 1); write(' надеть на '); print(sk); writeln end; begin {move} if n = 1 then step else begin move(n-1, sk, sw); step; move(n-1, sw, s 1, sk) end; begin read(m); {число дисков} writeln('для ', m: 3, ' дисков следует произвести ', 'следующие действия: '); move(m, left, middle, right); readln end. 31
Type st = (left, middle, right); nat = 1. . maxint; var m: nat; {m – число дисков} procedure move(n: nat; s 1, sw, sk: st); {перемещение n дисков с s 1 на sk} procedure step; {перемещение одного диска с s 1 на sk} procedure print(s: st); begin case s of left: write(' лев. '); middle: write(' средн. '); right: write(' прав. ') end; begin {step} write(' снять диск с '); print(s 1); write(' надеть на '); print(sk); writeln end; begin {move} if n = 1 then step else begin move(n-1, sk, sw); step; move(n-1, sw, s 1, sk) end; begin read(m); {число дисков} writeln('для ', m: 3, ' дисков следует произвести ', 'следующие действия: '); move(m, left, middle, right); readln end. 31
 32
32
 Переборные задачи. Рассмотрим программу, осуществляющую вывод всех k-значных двоичных чисел (их всего, очевидно, 2 k) var a: array[1. . 100] of integer; k: integer; procedure check; var j: integer; begin for j: =1 to k do write(a[j]); writeln; end; Procedure find(i: integer); begin if i>k then begin check; exit; end; a[i]: =0; find(i+1); a[i]: =1; find(i+1); end; begin readln(k); find(1); end. 33
Переборные задачи. Рассмотрим программу, осуществляющую вывод всех k-значных двоичных чисел (их всего, очевидно, 2 k) var a: array[1. . 100] of integer; k: integer; procedure check; var j: integer; begin for j: =1 to k do write(a[j]); writeln; end; Procedure find(i: integer); begin if i>k then begin check; exit; end; a[i]: =0; find(i+1); a[i]: =1; find(i+1); end; begin readln(k); find(1); end. 33
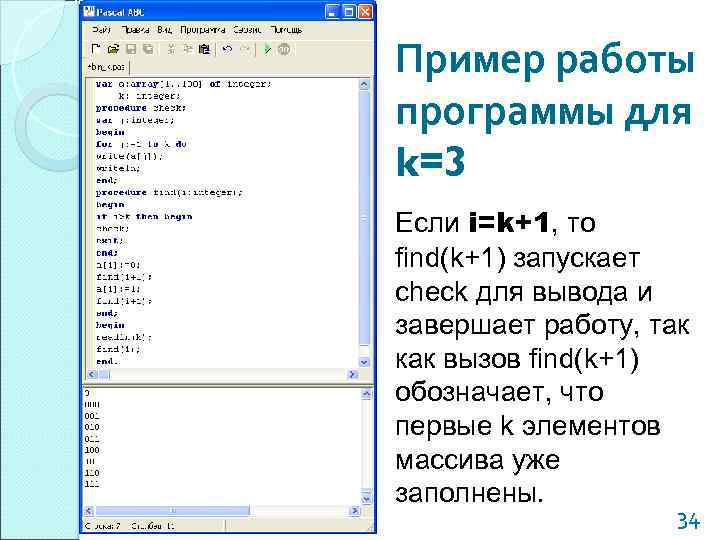 Пример работы программы для k=3 Если i=k+1, то find(k+1) запускает check для вывода и завершает работу, так как вызов find(k+1) обозначает, что первые k элементов массива уже заполнены. 34
Пример работы программы для k=3 Если i=k+1, то find(k+1) запускает check для вывода и завершает работу, так как вызов find(k+1) обозначает, что первые k элементов массива уже заполнены. 34
 Задача о расстановке n ферзей for i 1 : = 1 to n do begin ферзь[1] : = i 1; for i 2 : = 1 to n do begin ферзь[2] : = i 2; for i 3 : = 1 to n do begin ферзь[3] : = i 3; . . . <проверка построенной позиции> end; 35
Задача о расстановке n ферзей for i 1 : = 1 to n do begin ферзь[1] : = i 1; for i 2 : = 1 to n do begin ферзь[2] : = i 2; for i 3 : = 1 to n do begin ферзь[3] : = i 3; . . . <проверка построенной позиции> end; 35
![Отсечения при переборе for i 1 : = 1 to n do begin ферзь[1] Отсечения при переборе for i 1 : = 1 to n do begin ферзь[1]](https://present5.com/presentation/-36460169_139862956/image-36.jpg) Отсечения при переборе for i 1 : = 1 to n do begin ферзь[1] : = i 1; for i 2 : = 1 to n do begin ферзь[2] : = i 2; { проверка частично построенной позиции } if <ферзь[2] не бьёт ферзь[1]> then for i 3 : = 1 to n do begin ферзь[3] : = i 3; { проверка частично построенной позиции } if <ферзь[3] не бьёт предыдущих> then for i 4 : = 1 to n do begin. . . if <ферзь[n] не бьёт предыдущих> then <решение найдено> end; 3 6
Отсечения при переборе for i 1 : = 1 to n do begin ферзь[1] : = i 1; for i 2 : = 1 to n do begin ферзь[2] : = i 2; { проверка частично построенной позиции } if <ферзь[2] не бьёт ферзь[1]> then for i 3 : = 1 to n do begin ферзь[3] : = i 3; { проверка частично построенной позиции } if <ферзь[3] не бьёт предыдущих> then for i 4 : = 1 to n do begin. . . if <ферзь[n] не бьёт предыдущих> then <решение найдено> end; 3 6
 Решение задачи о n ферзях перебором с возвратом program Backtrack. Queens; var n : integer; { размер доски } queen : array[1. . 100] of integer; { массив положений ферзей } procedure Write. Solution; …{ Процедура печати решения } { Функция проверки совместимости m-го ферзя с предыдущими } function Check(m : integer) : boolean; … procedure Backtrack(m : integer); { Процедура перебора } var i : integer; begin if m > n then { найдено решение } Write. Solution else for i : = 1 to n do begin queen[m] : = i; if Check(m) then Backtrack(m+1); {m-тый не бьет пред. } end; 37 end;
Решение задачи о n ферзях перебором с возвратом program Backtrack. Queens; var n : integer; { размер доски } queen : array[1. . 100] of integer; { массив положений ферзей } procedure Write. Solution; …{ Процедура печати решения } { Функция проверки совместимости m-го ферзя с предыдущими } function Check(m : integer) : boolean; … procedure Backtrack(m : integer); { Процедура перебора } var i : integer; begin if m > n then { найдено решение } Write. Solution else for i : = 1 to n do begin queen[m] : = i; if Check(m) then Backtrack(m+1); {m-тый не бьет пред. } end; 37 end;
 Реализация Check и Write. Solution procedure Write. Solution; var i : integer; begin for i : = 1 to n do Write(queen[i], ' '); Write. Ln end; { Функция проверки совместимости m-го ферзя с предыдущими } function Check(m : integer) : boolean; var i : integer; begin for i : = 1 to m-1 do if (queen[i] = queen[m]) {совпадают горизонтали } Or (i+queen[i] = m+queen[m]) n=4 { нисходящие диагонали } 2 4 1 3 Or (i-queen[i] = m-queen[m]) 3 1 4 2 { восходящие диагонали } then begin Check : = False; Exit; end; Check : = True; 38
Реализация Check и Write. Solution procedure Write. Solution; var i : integer; begin for i : = 1 to n do Write(queen[i], ' '); Write. Ln end; { Функция проверки совместимости m-го ферзя с предыдущими } function Check(m : integer) : boolean; var i : integer; begin for i : = 1 to m-1 do if (queen[i] = queen[m]) {совпадают горизонтали } Or (i+queen[i] = m+queen[m]) n=4 { нисходящие диагонали } 2 4 1 3 Or (i-queen[i] = m-queen[m]) 3 1 4 2 { восходящие диагонали } then begin Check : = False; Exit; end; Check : = True; 38
 Задача о лабиринте Пример входных данных: 5 5 1 1 5 5 0 0 0 -1 -1 -1 0 0 0 0 -1 -1 0 0 0 Пример выходных данных: 1 0 0 2 -1 -1 -1 0 3 0 0 4 -1 -1 5 6 7 8 9 39
Задача о лабиринте Пример входных данных: 5 5 1 1 5 5 0 0 0 -1 -1 -1 0 0 0 0 -1 -1 0 0 0 Пример выходных данных: 1 0 0 2 -1 -1 -1 0 3 0 0 4 -1 -1 5 6 7 8 9 39
 Описание данных задачи о лабиринте Const maxn = 20; { макс размер лабиринта } { смещение } dx: array [1. . 4] of integer = (-1, 0, 1, 0); {влево-вниз-вправо-вверх} dy: array [1. . 4] of integer = ( 0, -1, 0, 1); var a: array [0. . maxn+1, 0. . maxn+1] of integer; n, m, { размеры лабиринта } sx, sy, { начальное положение } fx, fy: integer; { положение выхода } 40
Описание данных задачи о лабиринте Const maxn = 20; { макс размер лабиринта } { смещение } dx: array [1. . 4] of integer = (-1, 0, 1, 0); {влево-вниз-вправо-вверх} dy: array [1. . 4] of integer = ( 0, -1, 0, 1); var a: array [0. . maxn+1, 0. . maxn+1] of integer; n, m, { размеры лабиринта } sx, sy, { начальное положение } fx, fy: integer; { положение выхода } 40
 Процедуры ввода и инициализации данных и вывода procedure init; var i, j: integer; begin for i : = 0 to maxn+1 do {барьеры } for j : = 0 to maxn+1 do a[i, j] : = -1; read(n, m, sx, sy, fx, fy); for i : = 1 to m do for j : = 1 to n do procedure print_labirint; var i, j: integer; begin writeln; for i : = 1 to n do begin for j : = 1 to m do write(a[i, j]: 4); writeln; end; 41
Процедуры ввода и инициализации данных и вывода procedure init; var i, j: integer; begin for i : = 0 to maxn+1 do {барьеры } for j : = 0 to maxn+1 do a[i, j] : = -1; read(n, m, sx, sy, fx, fy); for i : = 1 to m do for j : = 1 to n do procedure print_labirint; var i, j: integer; begin writeln; for i : = 1 to n do begin for j : = 1 to m do write(a[i, j]: 4); writeln; end; 41
 Полный перебор с возвратами в решении задачи о лабиринте procedure search(x, y, k: integer); var i: integer; begin a[y, x] : = k; { запись варианта } if (x = fx) and (y = fy) then { решение найдено } begin print_labirint; { вывод решения } halt; end else for i : = 1 to 4 do { перебор всех вариантов } if a[y+dy[i], x+dx[i]] = 0 then Основная программа { вариант подходит } search(x+dx[i], y+dy[i], k+1); будет иметь вид: begin { рекурсивный вызов } init; a[y, x] : = 0; { стирание варианта } search(sx, sy, 1); end. 42
Полный перебор с возвратами в решении задачи о лабиринте procedure search(x, y, k: integer); var i: integer; begin a[y, x] : = k; { запись варианта } if (x = fx) and (y = fy) then { решение найдено } begin print_labirint; { вывод решения } halt; end else for i : = 1 to 4 do { перебор всех вариантов } if a[y+dy[i], x+dx[i]] = 0 then Основная программа { вариант подходит } search(x+dx[i], y+dy[i], k+1); будет иметь вид: begin { рекурсивный вызов } init; a[y, x] : = 0; { стирание варианта } search(sx, sy, 1); end. 42
 Модифицированная задача об укладке рюкзака Из заданных n предметов выбрать такие, чтобы их суммарная стоимость была не менее чем S, а суммарный объём не превосходил V. От классической она отличается тем, что не требуется искать максимальную стоимость предметов. Стоимости предметов будут храниться в массиве St , а объёмы – в массиве Ob. Пространством перебора в данном случае будут все подмножества {1, . . . , n}. Каждое подмножество можно задавать набором (x 1, . . . , xn), xi {0, 1}. Теперь задачу можно переформулировать в следующем виде. Найти набор (x 1, . . . , xn), xi {0, 1}, такой, что для ненулевых xi сумма их стоимостей St(i) >=S, а сумма объемов Ob(i)<=V. 43
Модифицированная задача об укладке рюкзака Из заданных n предметов выбрать такие, чтобы их суммарная стоимость была не менее чем S, а суммарный объём не превосходил V. От классической она отличается тем, что не требуется искать максимальную стоимость предметов. Стоимости предметов будут храниться в массиве St , а объёмы – в массиве Ob. Пространством перебора в данном случае будут все подмножества {1, . . . , n}. Каждое подмножество можно задавать набором (x 1, . . . , xn), xi {0, 1}. Теперь задачу можно переформулировать в следующем виде. Найти набор (x 1, . . . , xn), xi {0, 1}, такой, что для ненулевых xi сумма их стоимостей St(i) >=S, а сумма объемов Ob(i)<=V. 43
 Перебор с возвратом в модифицированной задаче о рюкзаке procedure перебор_с_возвратом(m : integer); var i : integer; begin if m > n then <найдено решение> else begin x[m] : = 0; { не берем предмет m!!! } ост_стоимость : = ост_стоимость+St[m]; if ост_стоимость <= доп_ост then перебор_с_возвратом(m+1); {берем предмет m!!} ост_стоимость : = ост_стоимость- St[m]; x[m] : = 1; сумм_объём : = сумм_объём+Ob[m]; if сумм_объём <= V then перебор_с_возвратом(m+1); сумм_объём : = сумм_объём-Ob[m]; end; 44
Перебор с возвратом в модифицированной задаче о рюкзаке procedure перебор_с_возвратом(m : integer); var i : integer; begin if m > n then <найдено решение> else begin x[m] : = 0; { не берем предмет m!!! } ост_стоимость : = ост_стоимость+St[m]; if ост_стоимость <= доп_ост then перебор_с_возвратом(m+1); {берем предмет m!!} ост_стоимость : = ост_стоимость- St[m]; x[m] : = 1; сумм_объём : = сумм_объём+Ob[m]; if сумм_объём <= V then перебор_с_возвратом(m+1); сумм_объём : = сумм_объём-Ob[m]; end; 44
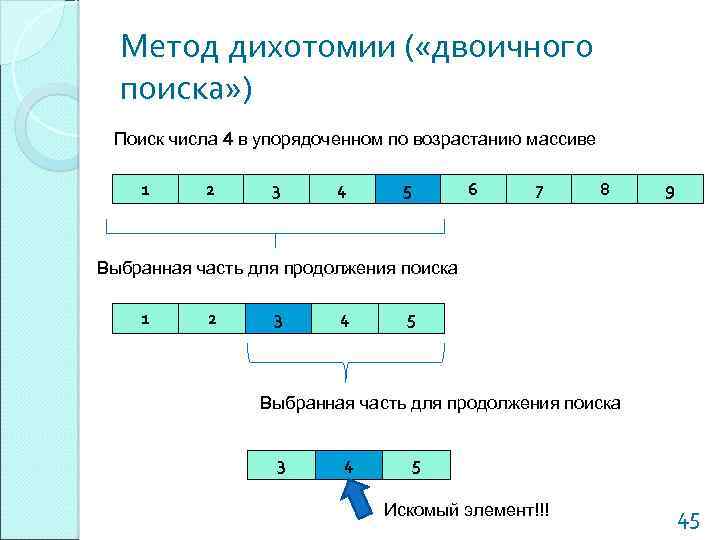 Метод дихотомии ( «двоичного поиска» ) Поиск числа 4 в упорядоченном по возрастанию массиве 1 2 3 4 5 6 7 8 9 Выбранная часть для продолжения поиска 1 2 3 4 5 Выбранная часть для продолжения поиска 3 4 5 Искомый элемент!!! 45
Метод дихотомии ( «двоичного поиска» ) Поиск числа 4 в упорядоченном по возрастанию массиве 1 2 3 4 5 6 7 8 9 Выбранная часть для продолжения поиска 1 2 3 4 5 Выбранная часть для продолжения поиска 3 4 5 Искомый элемент!!! 45
![Функция двоичного поиска и ее вызов type Data. Array=array[1. . 100] of real; var Функция двоичного поиска и ее вызов type Data. Array=array[1. . 100] of real; var](https://present5.com/presentation/-36460169_139862956/image-46.jpg) Функция двоичного поиска и ее вызов type Data. Array=array[1. . 100] of real; var a: Data. Array; n, i: integer; k: real; function BSearch (item: Data. Array; count: integer; key: real): integer; var low, high, mid: integer; found: boolean; Вызов Bsearch в главной begin программе: low: =1; high: =count; found: =false; { не найден } writeln('Input n'); while (low<=high) and (not found) do readln(n); begin writeln('Input sorted mid: =(low+high) div 2; array'); if key
Функция двоичного поиска и ее вызов type Data. Array=array[1. . 100] of real; var a: Data. Array; n, i: integer; k: real; function BSearch (item: Data. Array; count: integer; key: real): integer; var low, high, mid: integer; found: boolean; Вызов Bsearch в главной begin программе: low: =1; high: =count; found: =false; { не найден } writeln('Input n'); while (low<=high) and (not found) do readln(n); begin writeln('Input sorted mid: =(low+high) div 2; array'); if key
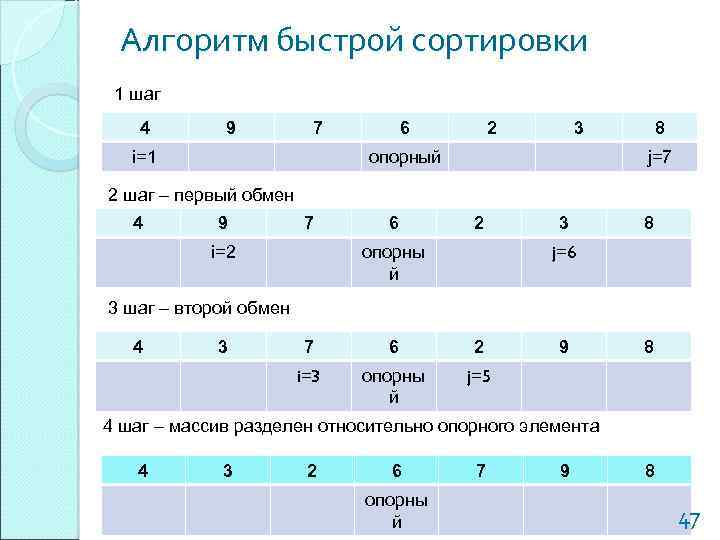 Алгоритм быстрой сортировки 1 шаг 4 9 7 i=1 6 2 3 опорный 8 j=7 2 шаг – первый обмен 4 9 7 i=2 6 2 3 8 j=6 опорны й 3 шаг – второй обмен 4 3 7 6 2 i=3 опорны й 9 8 j=5 4 шаг – массив разделен относительно опорного элемента 4 3 2 6 опорны й 7 9 8 47
Алгоритм быстрой сортировки 1 шаг 4 9 7 i=1 6 2 3 опорный 8 j=7 2 шаг – первый обмен 4 9 7 i=2 6 2 3 8 j=6 опорны й 3 шаг – второй обмен 4 3 7 6 2 i=3 опорны й 9 8 j=5 4 шаг – массив разделен относительно опорного элемента 4 3 2 6 опорны й 7 9 8 47
 Программа быстрой сортировки procedure Quick. Sort(var a: list; Lo, Hi: integer); procedure Sort(left, right: integer); var i, j, x : integer; y : integer; begin Главная программа: i : = left; j : = right; x : = a[(left + right) div 2]; const nn = 100; repeat type list = array[1. . nn] of while a[i] < x do i : = i + 1; integer; while x < a[j] do j : = j - 1; var a: list; i, n : integer; if i <= j then procedure Quick. Sort(var a: list; begin Lo, Hi: integer); y : = a[i]; a[i] : = a[j]; a[j] : = y; … i : = i + 1; j : = j - 1 begin{ Quick. Sort} end read(n); until i > j; for i : = 1 to n do read(a[i]); if left < j then Sort(left, j); Quick. Sort(a, 1, n); if i < right then Sort(i, right) writeln('Sorted'); end; for i : = 1 to n do begin {Quick. Sort}; write(a[i], ' '); Sort(Lo, Hi) end; 48
Программа быстрой сортировки procedure Quick. Sort(var a: list; Lo, Hi: integer); procedure Sort(left, right: integer); var i, j, x : integer; y : integer; begin Главная программа: i : = left; j : = right; x : = a[(left + right) div 2]; const nn = 100; repeat type list = array[1. . nn] of while a[i] < x do i : = i + 1; integer; while x < a[j] do j : = j - 1; var a: list; i, n : integer; if i <= j then procedure Quick. Sort(var a: list; begin Lo, Hi: integer); y : = a[i]; a[i] : = a[j]; a[j] : = y; … i : = i + 1; j : = j - 1 begin{ Quick. Sort} end read(n); until i > j; for i : = 1 to n do read(a[i]); if left < j then Sort(left, j); Quick. Sort(a, 1, n); if i < right then Sort(i, right) writeln('Sorted'); end; for i : = 1 to n do begin {Quick. Sort}; write(a[i], ' '); Sort(Lo, Hi) end; 48
![Простые примеры задач на динамическое программирование Var D : Array [1. . 50] of Простые примеры задач на динамическое программирование Var D : Array [1. . 50] of](https://present5.com/presentation/-36460169_139862956/image-49.jpg) Простые примеры задач на динамическое программирование Var D : Array [1. . 50] of Long. Int; Function F(X : integer) : Long. Int; Begin if D[X] = 0 then if (X = 1) or (X = 2) then D[X] : = 1 else D[X] : = F(x - 1) + F(x - 2); F : = D[X] end; Без рекурсии: D[1] : = 1; D[2] : = 1; For i : = 3 to X do D[i] : = D[i-1] + D[i-2]; 49
Простые примеры задач на динамическое программирование Var D : Array [1. . 50] of Long. Int; Function F(X : integer) : Long. Int; Begin if D[X] = 0 then if (X = 1) or (X = 2) then D[X] : = 1 else D[X] : = F(x - 1) + F(x - 2); F : = D[X] end; Без рекурсии: D[1] : = 1; D[2] : = 1; For i : = 3 to X do D[i] : = D[i-1] + D[i-2]; 49
 Задача о черепашке. Рекурсивное решение. function find(i, j): integer; var n 1, n 2: integer; begin if i=1 then begin if j=1 then find: =a[1, 1] Ч else find: =find(i, j-1)+a[i, j]; Запуск решения – exit; find(N, M) end; if j=1 then begin {can’t be 1 here} find: =find(i-1, j)+a[i, j]; exit; end; n 1: =find(i-1, j); n 2: =find(i, j-1); if n 1
Задача о черепашке. Рекурсивное решение. function find(i, j): integer; var n 1, n 2: integer; begin if i=1 then begin if j=1 then find: =a[1, 1] Ч else find: =find(i, j-1)+a[i, j]; Запуск решения – exit; find(N, M) end; if j=1 then begin {can’t be 1 here} find: =find(i-1, j)+a[i, j]; exit; end; n 1: =find(i-1, j); n 2: =find(i, j-1); if n 1
 Нерациональность перебора Запускается find(N, M) (из главной программы) Запускается find(N − 1, M) (из find(N, M)) Запускается find(N − 2, M) (из find(N − 1, M)) Запускается find(N − 3, M) (из find(N − 2, M)). . . Запускается find(N − 2, M − 1) (из find(N − 2, M)). . . Запускается find(N − 1, M − 1) (из find(N − 1, M)) Запускается find(N − 2, M − 1) (из find(N − 1, M − 1)). . . Запускается find(N − 1, M − 2) (из find(N − 1, M − 1)). . . Запускается find(N, M − 1) (из find(N, M)) Запускается find(N − 1, M − 1) (из find(N, M − 1)) Запускается find(N − 2, M − 1) (из find(N − 1, M − 1)). . . Запускается find(N − 1, M − 2) (из find(N − 1, M − 1)). . . Запускается find(N, M − 2) (из find(N, M − 1)) Запускается find(N − 1, M − 2) (из find(N, M − 2)). . . Запускается find(N, M − 3) (из find(N, M − 2)). . . 51
Нерациональность перебора Запускается find(N, M) (из главной программы) Запускается find(N − 1, M) (из find(N, M)) Запускается find(N − 2, M) (из find(N − 1, M)) Запускается find(N − 3, M) (из find(N − 2, M)). . . Запускается find(N − 2, M − 1) (из find(N − 2, M)). . . Запускается find(N − 1, M − 1) (из find(N − 1, M)) Запускается find(N − 2, M − 1) (из find(N − 1, M − 1)). . . Запускается find(N − 1, M − 2) (из find(N − 1, M − 1)). . . Запускается find(N, M − 1) (из find(N, M)) Запускается find(N − 1, M − 1) (из find(N, M − 1)) Запускается find(N − 2, M − 1) (из find(N − 1, M − 1)). . . Запускается find(N − 1, M − 2) (из find(N − 1, M − 1)). . . Запускается find(N, M − 2) (из find(N, M − 1)) Запускается find(N − 1, M − 2) (из find(N, M − 2)). . . Запускается find(N, M − 3) (из find(N, M − 2)). . . 51
 Решение методом ДП В варианте а) ответ для клетки (i, j) будет равен сумме ответов для клеток (i− 1, j) и (i, j − 1) (считаем столбцы занумерованы слева направо, а строки - снизу вверх); в варианте б) ответ для клетки (i, j) будет равен максимуму из ответов для клеток (i − 1, j) и (i, j − 1) плюс собственно значение, записанное изначально в клетке (i, j). То есть: а) ans[i, j] = ans[i− 1, j] + ans[i, j− 1]; б) ans[i, j] = max(ans[i− 1, j], ans[i, j− 1])+a[i, j], 52
Решение методом ДП В варианте а) ответ для клетки (i, j) будет равен сумме ответов для клеток (i− 1, j) и (i, j − 1) (считаем столбцы занумерованы слева направо, а строки - снизу вверх); в варианте б) ответ для клетки (i, j) будет равен максимуму из ответов для клеток (i − 1, j) и (i, j − 1) плюс собственно значение, записанное изначально в клетке (i, j). То есть: а) ans[i, j] = ans[i− 1, j] + ans[i, j− 1]; б) ans[i, j] = max(ans[i− 1, j], ans[i, j− 1])+a[i, j], 52
 ДП для задачи о черепашке Строки и столбцы нумеруем с единицы. Считаем, что координаты правого верхнего угла (N, M). Вариант а. ans[1, 1]: =1; for i: =2 to n do {сюда надо вставить начальные значения границы в ans[i, 1]} for i: =2 to m do {сюда надо вставить начальные значения границы в ans[1, i]} for i: =2 to n do for j: =2 to m do ans[i, j]: =ans[i-1, j]+ans[i, j-1]; Вариант б. ans[1, 1]: =a[1, 1]; for i: =2 to n do {сюда надо вставить начальные значения границы в ans[i, 1]} for i: =2 to m do {сюда надо вставить начальные значения границы в ans[1, i]} for i: =2 to n do for j: =2 to m do 53
ДП для задачи о черепашке Строки и столбцы нумеруем с единицы. Считаем, что координаты правого верхнего угла (N, M). Вариант а. ans[1, 1]: =1; for i: =2 to n do {сюда надо вставить начальные значения границы в ans[i, 1]} for i: =2 to m do {сюда надо вставить начальные значения границы в ans[1, i]} for i: =2 to n do for j: =2 to m do ans[i, j]: =ans[i-1, j]+ans[i, j-1]; Вариант б. ans[1, 1]: =a[1, 1]; for i: =2 to n do {сюда надо вставить начальные значения границы в ans[i, 1]} for i: =2 to m do {сюда надо вставить начальные значения границы в ans[1, i]} for i: =2 to n do for j: =2 to m do 53
 Жадные алгоритмы Жадный алгоритм (greedy algorithm) – это метод решения оптимизационных задач, основанный на том, что процесс решения задачи можно разбить на шаги, на каждом из которых принимается решение. Решение, принимаемое на каждом шаге, должно быть оптимальным только на текущем шаге, и должно приниматься вне зависимости от решений на других шагах. На каждом шаге «жадный» алгоритм выбирает локально оптимальное в том или ином смысле решение. 54
Жадные алгоритмы Жадный алгоритм (greedy algorithm) – это метод решения оптимизационных задач, основанный на том, что процесс решения задачи можно разбить на шаги, на каждом из которых принимается решение. Решение, принимаемое на каждом шаге, должно быть оптимальным только на текущем шаге, и должно приниматься вне зависимости от решений на других шагах. На каждом шаге «жадный» алгоритм выбирает локально оптимальное в том или ином смысле решение. 54
 Дискретная и непрерывная задача о рюкзаке Постановка дискретной задачи. В рюкзак загружаются предметы n различных типов (количество предметов каждого типа не ограничено). Максимальный вес рюкзака W. Каждый предмет типа i имеет вес wi и стоимость vi (i=1, 2, . . . , n). Требуется определить максимальную стоимость груза, вес которого не превышает W. Обозначим количество предметов типа i через ki, тогда требуется максимизировать v 1*k 1+v 2*k 2+. . . +vn*kn при ограничениях w 1*k 1+w 2*k 2+. . . +wn*kn W, где ki - целые (0 ki [W/wi]), квадратные скобки означают 55 целую часть числа.
Дискретная и непрерывная задача о рюкзаке Постановка дискретной задачи. В рюкзак загружаются предметы n различных типов (количество предметов каждого типа не ограничено). Максимальный вес рюкзака W. Каждый предмет типа i имеет вес wi и стоимость vi (i=1, 2, . . . , n). Требуется определить максимальную стоимость груза, вес которого не превышает W. Обозначим количество предметов типа i через ki, тогда требуется максимизировать v 1*k 1+v 2*k 2+. . . +vn*kn при ограничениях w 1*k 1+w 2*k 2+. . . +wn*kn W, где ki - целые (0 ki [W/wi]), квадратные скобки означают 55 целую часть числа.
 Сonst Max. N=10; Va r n, w: integer; {количество предметов, максимальный вес} Weight, Price: array[1. . Max. N] of integer; {вес, стоимость предметов} Best, Now: array[1. . Max. N] of integer; {наилучшее, текущее решения} Max. Price: Long. Int; {наибольшая стоимость} Procedure Rec(k, w: integer; st: Long. Int); {процедура перебора: } {k - порядковый номер группы предметов, w - вес, который следует набрать из оставшихся предметов, st - стоимость текущего решения} var i: integer; begin if (k>n) and (st>Max. Price) then begin { если наполнили рюкзак и набрали стоимость больше чем имеется, то считаем это новым решением } Best: =Now; Max. Price: =st; end {иначе если количество взятых < объема. заполняем рюкзак дальше} else if k<=n then {иначе если набрано меньше чем входит} for i: =0 to w div Weight[k] do begin Now[k]: =i; {берем предмет i пока есть место в ранце} 5 Rec(k+1, W-i*Weight[k], st+i*Price[k]); 6 {после каждого взятия предмета увеличиваем стоимость набора и
Сonst Max. N=10; Va r n, w: integer; {количество предметов, максимальный вес} Weight, Price: array[1. . Max. N] of integer; {вес, стоимость предметов} Best, Now: array[1. . Max. N] of integer; {наилучшее, текущее решения} Max. Price: Long. Int; {наибольшая стоимость} Procedure Rec(k, w: integer; st: Long. Int); {процедура перебора: } {k - порядковый номер группы предметов, w - вес, который следует набрать из оставшихся предметов, st - стоимость текущего решения} var i: integer; begin if (k>n) and (st>Max. Price) then begin { если наполнили рюкзак и набрали стоимость больше чем имеется, то считаем это новым решением } Best: =Now; Max. Price: =st; end {иначе если количество взятых < объема. заполняем рюкзак дальше} else if k<=n then {иначе если набрано меньше чем входит} for i: =0 to w div Weight[k] do begin Now[k]: =i; {берем предмет i пока есть место в ранце} 5 Rec(k+1, W-i*Weight[k], st+i*Price[k]); 6 {после каждого взятия предмета увеличиваем стоимость набора и
 Непрерывная задача о рюкзаке Жадный алгоритм: 1. Вычислим цены всех предметов - стоимость предмета разделим на массу (Price[i]/Weight[i]). 2. Сначала берем самый дорогой предмет и наполняем им рюкзак, если предмет закончился, а рюкзак не заполнен, берем следующий по цене, и так далее, пока не наберем максимально возможную суммарную массу предметов. Для сортировки понадобится O(N·log(N)) операций. В цикле по i от 1 до N и попробовать взять предмет i — займет еще O(n) операций. Итого, общая сложность — O(N·log(N) + N), что в общем случае эквивалентно O(N·log(N)). 57
Непрерывная задача о рюкзаке Жадный алгоритм: 1. Вычислим цены всех предметов - стоимость предмета разделим на массу (Price[i]/Weight[i]). 2. Сначала берем самый дорогой предмет и наполняем им рюкзак, если предмет закончился, а рюкзак не заполнен, берем следующий по цене, и так далее, пока не наберем максимально возможную суммарную массу предметов. Для сортировки понадобится O(N·log(N)) операций. В цикле по i от 1 до N и попробовать взять предмет i — займет еще O(n) операций. Итого, общая сложность — O(N·log(N) + N), что в общем случае эквивалентно O(N·log(N)). 57
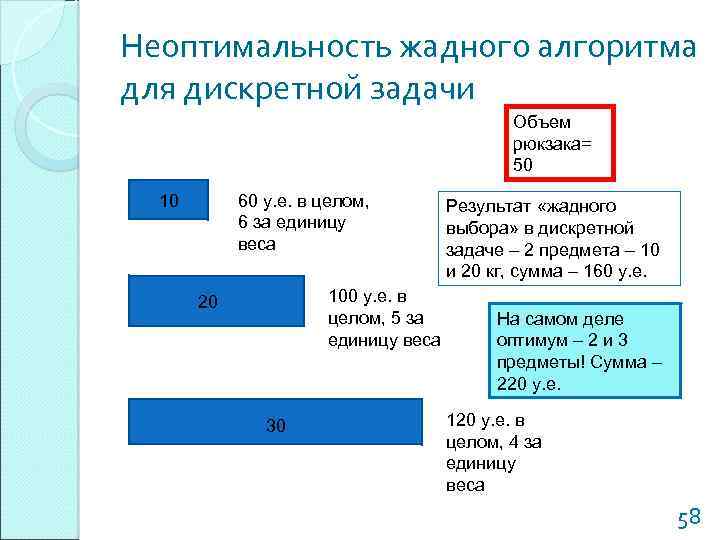 Неоптимальность жадного алгоритма для дискретной задачи Объем рюкзака= 50 10 60 y. е. в целом, 6 за единицу веса 100 у. е. в целом, 5 за единицу веса 20 30 Результат «жадного выбора» в дискретной задаче – 2 предмета – 10 и 20 кг, сумма – 160 у. е. На самом деле оптимум – 2 и 3 предметы! Сумма – 220 у. е. 120 у. е. в целом, 4 за единицу веса 58
Неоптимальность жадного алгоритма для дискретной задачи Объем рюкзака= 50 10 60 y. е. в целом, 6 за единицу веса 100 у. е. в целом, 5 за единицу веса 20 30 Результат «жадного выбора» в дискретной задаче – 2 предмета – 10 и 20 кг, сумма – 160 у. е. На самом деле оптимум – 2 и 3 предметы! Сумма – 220 у. е. 120 у. е. в целом, 4 за единицу веса 58
 Размер задачи, временная сложность Алгоритмическая временная сложность — это зависимость времени исполнения алгоритма от длины или количества входных данных, называемых размером задачи. Измеряется время числом элементарных шагов. Каждый элементарный шаг связан с операцией, выполняемой в алгоритме. 59
Размер задачи, временная сложность Алгоритмическая временная сложность — это зависимость времени исполнения алгоритма от длины или количества входных данных, называемых размером задачи. Измеряется время числом элементарных шагов. Каждый элементарный шаг связан с операцией, выполняемой в алгоритме. 59
 Оценка временной сложности операторов программы Tif = Tv+max(Tthen+1, Telse). 1 операция по ветке Then соответствует операции безусловного перехода. Tfor = Tv 1 + Tv 2+1 + k(Tтело +4), где k – количество итераций цикла, 1 до цикла соответствует начальному присваиванию, 4 операции в цикле – сравнение параметра цикла с выражением V 2, условный переход на тело цикла, увеличение счетчика цикла и безусловный переход на начало цикла. ПРИМЕР: for i: =1 to 100 do for j: =1 to 3 do s: =s+a[i, j]; Его временная сложность равна 1+100(4+1+3*(4+2))=2301 операций. 60
Оценка временной сложности операторов программы Tif = Tv+max(Tthen+1, Telse). 1 операция по ветке Then соответствует операции безусловного перехода. Tfor = Tv 1 + Tv 2+1 + k(Tтело +4), где k – количество итераций цикла, 1 до цикла соответствует начальному присваиванию, 4 операции в цикле – сравнение параметра цикла с выражением V 2, условный переход на тело цикла, увеличение счетчика цикла и безусловный переход на начало цикла. ПРИМЕР: for i: =1 to 100 do for j: =1 to 3 do s: =s+a[i, j]; Его временная сложность равна 1+100(4+1+3*(4+2))=2301 операций. 60
 Класс и порядок сложности Определение. Множество вычислительных проблем, для которых существуют алгоритмы, схожие по сложности, называется классом сложности. При оценке эффективности алгоритма вычисление точного значения функции временной сложности f(n) может быть трудно, поэтому используются методы аппроксимации для определения верхней границы функции. Пусть имеется функция g(n) и константа К такая, что K*g(n) превышает f(n) по мере того, как n значительно возрастает. Определение. Функция f(n) имеет порядок O(g(n)), если имеется константа К и счетчик n 0, такие, что f(n) < K*g(n), для n > n 0. 61
Класс и порядок сложности Определение. Множество вычислительных проблем, для которых существуют алгоритмы, схожие по сложности, называется классом сложности. При оценке эффективности алгоритма вычисление точного значения функции временной сложности f(n) может быть трудно, поэтому используются методы аппроксимации для определения верхней границы функции. Пусть имеется функция g(n) и константа К такая, что K*g(n) превышает f(n) по мере того, как n значительно возрастает. Определение. Функция f(n) имеет порядок O(g(n)), если имеется константа К и счетчик n 0, такие, что f(n) < K*g(n), для n > n 0. 61
 Порядок сложности нерекурсивных и рекурсивных функций s=0; for i: =1 to n do for j: =1 to m do s=s+1; Временная сложность O(n*m) Временная сложность для рекурсивных программ также является рекурсивной функцией: T(n 0)=const - нет рекурсивного хода T(n)=f(T(g(n)) – при рекурсивном вызове. 62
Порядок сложности нерекурсивных и рекурсивных функций s=0; for i: =1 to n do for j: =1 to m do s=s+1; Временная сложность O(n*m) Временная сложность для рекурсивных программ также является рекурсивной функцией: T(n 0)=const - нет рекурсивного хода T(n)=f(T(g(n)) – при рекурсивном вызове. 62
 Грубая оценка временной сложности рекурсивной программы Если верны соотношения T(1)=d; T(n)=a*T(n/c)+b*n, то в зависимости от констант а и с выражение для сложности имеет вид: 0(n) при a
Грубая оценка временной сложности рекурсивной программы Если верны соотношения T(1)=d; T(n)=a*T(n/c)+b*n, то в зависимости от констант а и с выражение для сложности имеет вид: 0(n) при a
 Классы сложности алгоритмов О(1) - количество шагов алгоритма не зависит от количества входных данных. Обычно это алгоритмы, использующие определённую часть данных и игнорирующие все остальные данные. Например, анализ одного элемента массива вне зависимости от количества элементов; О(log 2 n) – алгоритм двоичного поиска; О(n) - алгоритм линейной сложности, когда для каждого входного объекта выполняется только одно действие; О(n log 2 n) - такую сложность имеет алгоритм быстрой сортировки; O(n 2) - квадратичные алгоритмы. В основном, все простейшие алгоритмы сортировки. O(nx) - полиномиальные алгоритмы. O(xn) - экспоненциальные алгоритмы. О(n!) - факториальные алгоритмы. 64
Классы сложности алгоритмов О(1) - количество шагов алгоритма не зависит от количества входных данных. Обычно это алгоритмы, использующие определённую часть данных и игнорирующие все остальные данные. Например, анализ одного элемента массива вне зависимости от количества элементов; О(log 2 n) – алгоритм двоичного поиска; О(n) - алгоритм линейной сложности, когда для каждого входного объекта выполняется только одно действие; О(n log 2 n) - такую сложность имеет алгоритм быстрой сортировки; O(n 2) - квадратичные алгоритмы. В основном, все простейшие алгоритмы сортировки. O(nx) - полиномиальные алгоритмы. O(xn) - экспоненциальные алгоритмы. О(n!) - факториальные алгоритмы. 64
 Временная сложность рекурсивного алгоритма для задачи «Ханойские башни» Решение задачи для n дисков сводится к решению двух подзадач и одному ходу. Обе подзадачи имеют не половинный размер, а размер, лишь на единицу меньший исходного. Подсчитаем требуемое число ходов T(n). С учетом структуры решения: T(n) = 2 T(n-1) +Tход а=2, с=n/(n-1), следовательно a>c, и задача имеет экспоненциальный порядок сложности. По индукции можно доказать, что T(n)=2 n-1+2 n-2+… 2+1=2 n-1. 65
Временная сложность рекурсивного алгоритма для задачи «Ханойские башни» Решение задачи для n дисков сводится к решению двух подзадач и одному ходу. Обе подзадачи имеют не половинный размер, а размер, лишь на единицу меньший исходного. Подсчитаем требуемое число ходов T(n). С учетом структуры решения: T(n) = 2 T(n-1) +Tход а=2, с=n/(n-1), следовательно a>c, и задача имеет экспоненциальный порядок сложности. По индукции можно доказать, что T(n)=2 n-1+2 n-2+… 2+1=2 n-1. 65
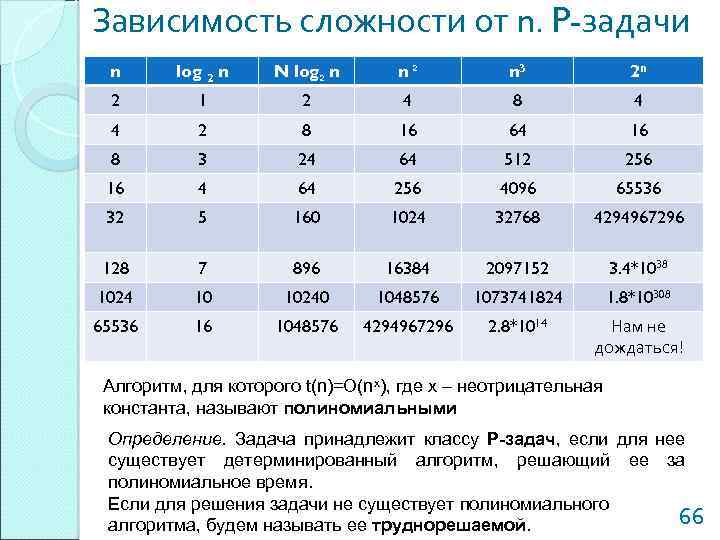 Зависимость сложности от n. P-задачи n log 2 n N log 2 n n 2 n 3 2 n 2 1 2 4 8 4 4 2 8 16 64 16 8 3 24 64 512 256 16 4 64 256 4096 65536 32 5 160 1024 32768 4294967296 128 7 896 16384 2097152 3. 4*1038 1024 10 10240 1048576 1073741824 1. 8*10308 65536 16 1048576 4294967296 2. 8*1014 Нам не дождаться! Алгоритм, для которого t(n)=O(nx), где x – неотрицательная константа, называют полиномиальными Определение. Задача принадлежит классу P-задач, если для нее существует детерминированный алгоритм, решающий ее за полиномиальное время. Если для решения задачи не существует полиномиального 66 алгоритма, будем называть ее труднорешаемой.
Зависимость сложности от n. P-задачи n log 2 n N log 2 n n 2 n 3 2 n 2 1 2 4 8 4 4 2 8 16 64 16 8 3 24 64 512 256 16 4 64 256 4096 65536 32 5 160 1024 32768 4294967296 128 7 896 16384 2097152 3. 4*1038 1024 10 10240 1048576 1073741824 1. 8*10308 65536 16 1048576 4294967296 2. 8*1014 Нам не дождаться! Алгоритм, для которого t(n)=O(nx), где x – неотрицательная константа, называют полиномиальными Определение. Задача принадлежит классу P-задач, если для нее существует детерминированный алгоритм, решающий ее за полиномиальное время. Если для решения задачи не существует полиномиального 66 алгоритма, будем называть ее труднорешаемой.
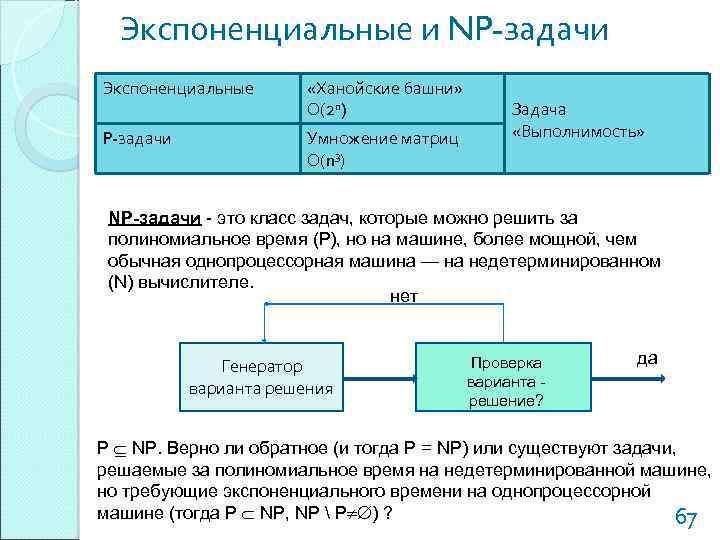 Экспоненциальные и NP-задачи Экспоненциальные «Ханойские башни» О(2 n) P-задачи Умножение матриц О(n 3) Задача «Выполнимость» NP-задачи - это класс задач, которые можно решить за полиномиальное время (Р), но на машине, более мощной, чем обычная однопроцессорная машина — на недетерминированном (N) вычислителе. нет Генератор варианта решения Проверка варианта решение? да P NP. Верно ли обратное (и тогда Р = NP) или существуют задачи, решаемые за полиномиальное время на недетерминированной машине, но требующие экспоненциального времени на однопроцессорной машине (тогда Р NP, NP Р ) ? 67
Экспоненциальные и NP-задачи Экспоненциальные «Ханойские башни» О(2 n) P-задачи Умножение матриц О(n 3) Задача «Выполнимость» NP-задачи - это класс задач, которые можно решить за полиномиальное время (Р), но на машине, более мощной, чем обычная однопроцессорная машина — на недетерминированном (N) вычислителе. нет Генератор варианта решения Проверка варианта решение? да P NP. Верно ли обратное (и тогда Р = NP) или существуют задачи, решаемые за полиномиальное время на недетерминированной машине, но требующие экспоненциального времени на однопроцессорной машине (тогда Р NP, NP Р ) ? 67
 NP-полные задачи Задача Т называется NP-полной, если она удовлетворяет двум условиям: 1) Т NP; 2) Если некоторая задача R NP, то R сводится к T за полиномиальное время. Сводимость означает следующее. Задача А сводится к задаче В, если из решения В можно получить решение А. Если поставленная задача А сводится с помощью алгоритма с полиномиальной сложностью к задаче B, то любой полиномиальный алгоритм решения B может быть превращен в полиномиальный алгоритм для А. Если не существует алгоритма для решения А, то его не существует и для В. Основная теорема. Если некоторая NP – полная задача разрешима за полиномиальное время, то Р = NP. Иначе говоря, если в классе NP есть задача, не разрешимая за полиномиальное время, то все NP – полные задачи таковы. 68
NP-полные задачи Задача Т называется NP-полной, если она удовлетворяет двум условиям: 1) Т NP; 2) Если некоторая задача R NP, то R сводится к T за полиномиальное время. Сводимость означает следующее. Задача А сводится к задаче В, если из решения В можно получить решение А. Если поставленная задача А сводится с помощью алгоритма с полиномиальной сложностью к задаче B, то любой полиномиальный алгоритм решения B может быть превращен в полиномиальный алгоритм для А. Если не существует алгоритма для решения А, то его не существует и для В. Основная теорема. Если некоторая NP – полная задача разрешима за полиномиальное время, то Р = NP. Иначе говоря, если в классе NP есть задача, не разрешимая за полиномиальное время, то все NP – полные задачи таковы. 68
 Задача «Выполнимость» . Примеры NPполных задач ПРОБЛЕМА ВЫПОЛНИМОСТИ или задача о дизъюнкциях. Дано конечное множество переменных Х 1, …, ХN. Дан набор дизъюнкций, составленных из этих переменных D 1, …, Dm. Существует ли для Х 1, …, ХN набор значений истинности, при котором выполняются (истинны) все дизъюнкции из множества D? Примеры NP-полных задач: 1. Гамильтонов цикл. Дан граф G c n вершинами. Существует ли в графе простой цикл, проходящий через все вершины графа? Простым называется цикл, в котором вершины не повторяются. Таким образом, гамильтонов цикл — это последовательность вершин и дуг (ребер) графа, содержащая все вершины графа G по одному разу, но, может быть, содержащая не все дуги. 2. Задача коммивояжера. Дан граф G с п вершинами. Каждому ребру графа приписано положительное целое число di , задающее длину ребра. Кроме этого, задано некоторое положительное целое число L. Требуется ответить на вопрос: найдется ли в графе G маршрут, проходящий через все вершины графа G , такой, что его длина не превышает L? Игры : пятнашки, тетрис, сапер. 69
Задача «Выполнимость» . Примеры NPполных задач ПРОБЛЕМА ВЫПОЛНИМОСТИ или задача о дизъюнкциях. Дано конечное множество переменных Х 1, …, ХN. Дан набор дизъюнкций, составленных из этих переменных D 1, …, Dm. Существует ли для Х 1, …, ХN набор значений истинности, при котором выполняются (истинны) все дизъюнкции из множества D? Примеры NP-полных задач: 1. Гамильтонов цикл. Дан граф G c n вершинами. Существует ли в графе простой цикл, проходящий через все вершины графа? Простым называется цикл, в котором вершины не повторяются. Таким образом, гамильтонов цикл — это последовательность вершин и дуг (ребер) графа, содержащая все вершины графа G по одному разу, но, может быть, содержащая не все дуги. 2. Задача коммивояжера. Дан граф G с п вершинами. Каждому ребру графа приписано положительное целое число di , задающее длину ребра. Кроме этого, задано некоторое положительное целое число L. Требуется ответить на вопрос: найдется ли в графе G маршрут, проходящий через все вершины графа G , такой, что его длина не превышает L? Игры : пятнашки, тетрис, сапер. 69


