Algorithms for Nearest Neighbor Search Piotr Indyk MIT

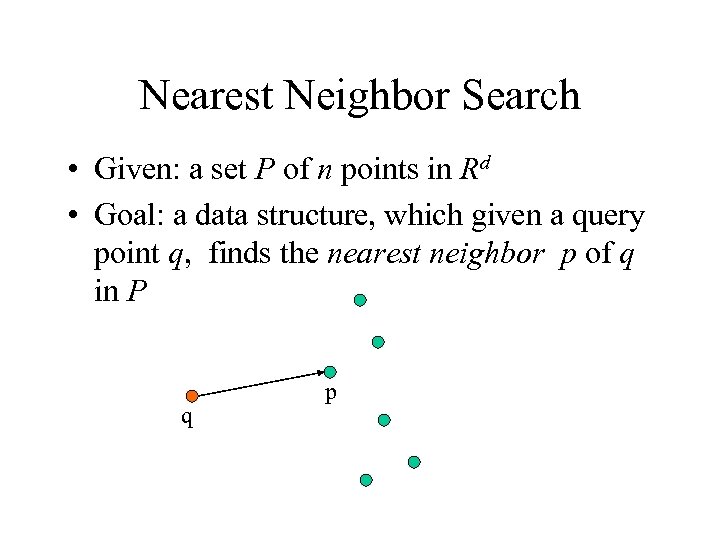
Nearest Neighbor Search • Given: a set P of n points in Rd • Goal: a data structure, which given a query point q, finds the nearest neighbor p of q in P q p

Outline of this talk • Variants • Motivation • Main memory algorithms: – quadtrees – kd-trees – Locality Sensitive Hashing • Secondary storage algorithms: – R-tree (and its variants) – VA-file

Variants of nearest neighbor • Near neighbor (range search): find one/all points in P within distance r from q • Spatial join: given two sets P, Q, find all pairs p in P, q in Q, such that p is within distance r from q • Approximate near neighbor: find one/all points p’ in P, whose distance to q is at most (1+e) times the distance from q to its nearest neighbor

Motivation Depends on the value of d: • low d: graphics, vision, GIS, etc • high d: – similarity search in databases (text, images etc) – finding pairs of similar objects (e. g. , copyright violation detection) – useful subroutine for clustering

Algorithms • Main memory (Computational Geometry) – linear scan – tree-based: • quadtree • kd-tree – hashing-based: Locality-Sensitive Hashing • Secondary storage (Databases) – R-tree (and numerous variants) – Vector Approximation File (VA-file)

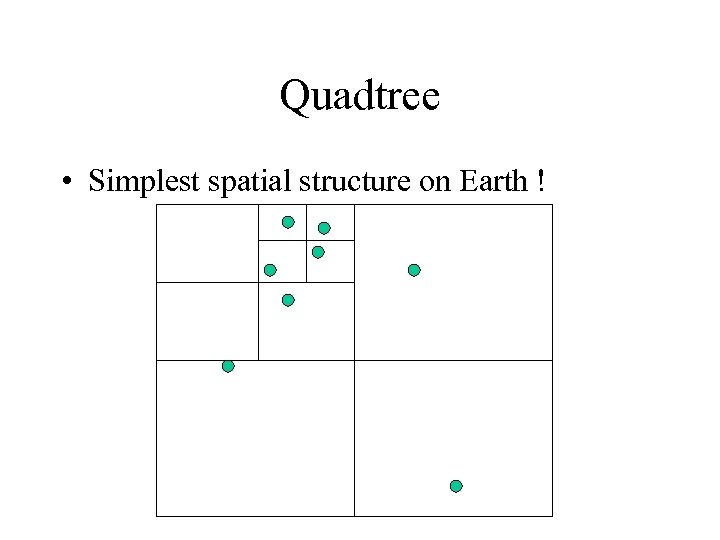
Quadtree • Simplest spatial structure on Earth !

Quadtree ctd. • Split the space into 2 d equal subsquares • Repeat until done: – only one pixel left – only one point left – only a few points left • Variants: – split only one dimension at a time – k-d-trees (in a moment)

Range search • Near neighbor (range search): – put the root on the stack – repeat • pop the next node T from the stack • for each child C of T: – if C is a leaf, examine point(s) in C – if C intersects with the ball of radius r around q, add C to the stack

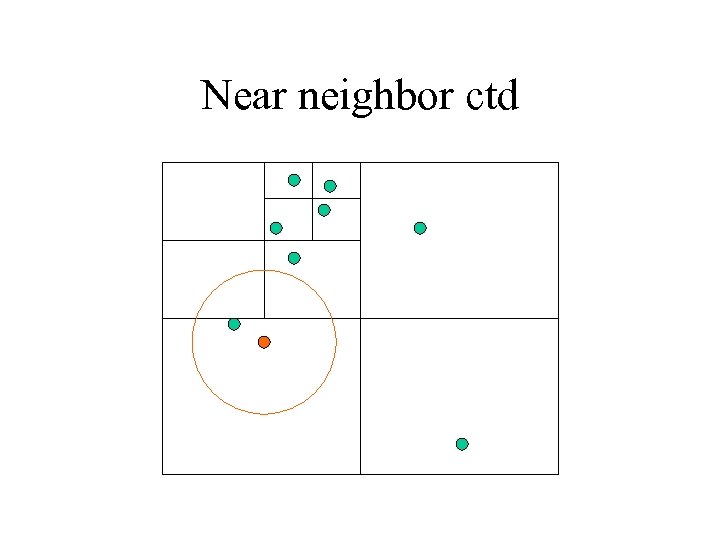
Near neighbor ctd

Nearest neighbor • Start range search with r = • Whenever a point is found, update r • Only investigate nodes with respect to current r

Quadtree ctd. • Simple data structure • Versatile, easy to implement • So why doesn’t this talk end here ? – Empty spaces: if the points form sparse clouds, it takes a while to reach them – Space exponential in dimension – Time exponential in dimension, e. g. , points on the hypercube

Space issues: example

K-d-trees [Bentley’ 75] • Main ideas: – only one-dimensional splits – instead of splitting in the middle, choose the split “carefully” (many variations) – near(est) neighbor queries: as for quadtrees • Advantages: – no (or less) empty spaces – only linear space • Exponential query time still possible

Exponential query time • What does it mean exactly ? – Unless we do something really stupid, query time is at most dn – Therefore, the actual query time is Min[ dn, exponential(d) ] • This is still quite bad though, when the dimension is around 20 -30 • Unfortunately, it seems inevitable (both in theory and practice)

Approximate nearest neighbor • Can do it using (augmented) k-d trees, by interrupting search earlier [Arya et al’ 94] • Still exponential time (in the worst case)! • Try a different approach: – for exact queries, we can use binary search trees or hashing – can we adapt hashing to nearest neighbor search ?

Locality-Sensitive Hashing [Indyk-Motwani’ 98] • Hash functions are locality-sensitive, if, for a random hash random function h, for any pair of points p, q we have: – Pr[h(p)=h(q)] is “high” if p is “close” to q – Pr[h(p)=h(q)] is “low” if p is”far” from q

Do such functions exist ? • Consider the hypercube, i. e. , – points from {0, 1}d – Hamming distance D(p, q)= # positions on which p and q differ • Define hash function h by choosing a set I of k random coordinates, and setting h(p) = projection of p on I

Example • Take – d=10, p=0101110010 – k=2, I={2, 5} • Then h(p)=11

h’s are locality-sensitive • Pr[h(p)=h(q)]=(1 -D(p, q)/d)k • We can vary the probability by changing k Pr k=1 distance Pr k=2 distance

How can we use LSH ? • Choose several h 1. . hl • Initialize a hash array for each hi • Store each point p in the bucket hi(p) of the i -th hash array, i=1. . . l • In order to answer query q – for each i=1. . l, retrieve points in a bucket hi(q) – return the closest point found

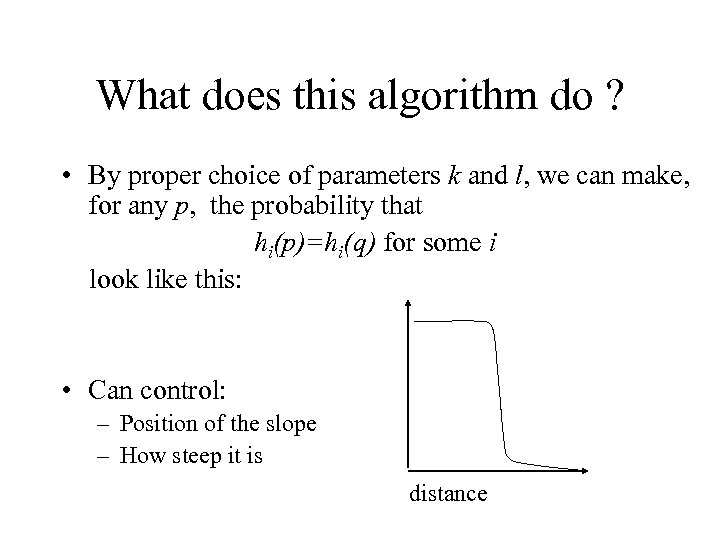
What does this algorithm do ? • By proper choice of parameters k and l, we can make, for any p, the probability that hi(p)=hi(q) for some i look like this: • Can control: – Position of the slope – How steep it is distance

The LSH algorithm • Therefore, we can solve (approximately) the near neighbor problem with given parameter r • Worst-case analysis guarantees dn 1/(1+e) query time • Practical evaluation indicates much better behavior [GIM’ 99, HGI’ 00, Buh’ 00, BT’ 00] • Drawbacks: • works best for Hamming distance (although can be generalized to Euclidean space) • requires radius r to be fixed in advance

Secondary storage • Seek time same as time needed to transfer hundreds of KBs • Grouping the data is crucial • Different approach required: – in main memory, any reduction in the number of inspected points was good – on disk, this is not the case !

Disk-based algorithms • R-tree [Guttman’ 84] – departing point for many variations – over 600 citations ! (according to Cite. Seer) – “optimistic” approach: try to answer queries in logarithmic time • Vector Approximation File [WSB’ 98] – “pessimistic” approach: if we need to scan the whole data set, we better do it fast • LSH works also on disk

R-tree • “Bottom-up” approach (k-d-tree was “topdown”) : – Start with a set of points/rectangles – Partition the set into groups of small cardinality – For each group, find minimum rectangle containing objects from this group – Repeat

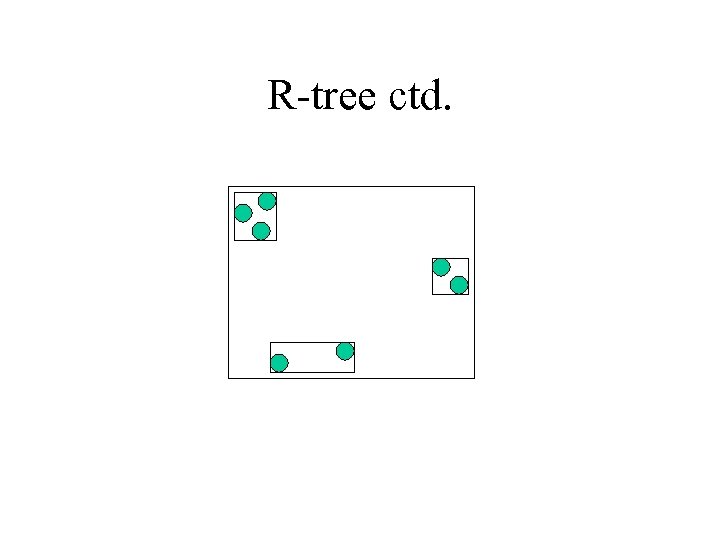
R-tree ctd.

R-tree ctd. • Advantages: – Supports near(est) neighbor search (similar as before) – Works for points and rectangles – Avoids empty spaces – Many variants: X-tree, SS-tree, SR-tree etc – Works well for low dimensions • Not so great for high dimensions

VA-file [Weber, Schek, Blott’ 98] • Approach: – In high-dimensional spaces, all tree-based indexing structures examine large fraction of leaves – If we need to visit so many nodes anyway, it is better to scan the whole data set and avoid performing seeks altogether – 1 seek = transfer of few hundred KB

VA-file ctd. • Natural question: how to speed-up linear scan ? • Answer: use approximation – Use only i bits per dimension (and speed-up the scan by a factor of 32/i) – Identify all points which could be returned as an answer – Verify the points using original data set

Time to sum up • “Curse of dimensionality” is indeed a curse • In main memory, we can perform sublinear-time search using trees or hashing • In secondary storage, linear scan is pretty much all we can do (for high dim) • Personal thought: if linear search is all we can do, we are not doing too well…. • Maybe it is time to buy a few GB of RAM • . . but at the end everything depends on your data set

Resources • Surveys: – Berchtold & Keim: – http: //www. informatik. unihalle. de/~keim/PS/ICDE 00. pdf – Theodoridis: – http: //dias. cti. gr/~ytheod/research/ADBIS/handouts. pdf – Agarwal et al (range searching): – http: //www. cs. duke. edu/~pankaj/papers. html

Resources • Source code: http: //dias. cti. gr/~ytheod/research/indexing/ http: //www. cs. sunysb. edu/~algorith/major_section/1. 6. shtml • References: see surveys plus very recent – [Buh’ 00, BT’ 00]: J. Buhler et al: http: //www. cs. washington. edu/homes/jbuhler/ – [HGI’ 00]: Haveliwala et al: http: //theory. lcs. mit. edu/~indyk/webdb. ps

Contact • If you have any question, feel free to e-mail me at indyk@theory. lcs. mit. edu • Thank you !