Algorithmic Game Theory Polynomial Time Algorithms and Internet

Algorithmic Game Theory Polynomial Time Algorithms and Internet Computing For Market Equilibria Vijay V. Vazirani

Markets

Stock Markets

Internet

n Revolution in definition of markets

n Revolution in definition of markets n New markets defined by ¨ Google ¨ Amazon ¨ Yahoo! ¨ Ebay

n Revolution in definition of markets n Massive computational power available

n Revolution in definition of markets n Massive computational power available n Important to find good models and algorithms for these markets

Adwords Market n Created by search engine companies ¨ Google ¨ Yahoo! ¨ MSN n Multi-billion dollar market n Totally revolutionized advertising, especially by small companies.

How will this market evolve? ?

n The study of market equilibria has occupied center stage within Mathematical Economics for over a century.

n The study of market equilibria has occupied center stage within Mathematical Economics for over a century. n This talk: Historical perspective & key notions from this theory.

2). Algorithmic Game Theory n Combinatorial algorithms for traditional market models

3). New Market Models n Resource Allocation Model of Kelly, 1997

3). New Market Models n Resource Allocation Model of Kelly, 1997 n For mathematically modeling TCP congestion control n Highly successful theory

A Capitalistic Economy Depends crucially on pricing mechanisms to ensure: Stability n Efficiency n Fairness n

Adam Smith n The Wealth of Nations 2 volumes, 1776.

Adam Smith n The Wealth of Nations 2 volumes, 1776. n ‘invisible hand’ of the market

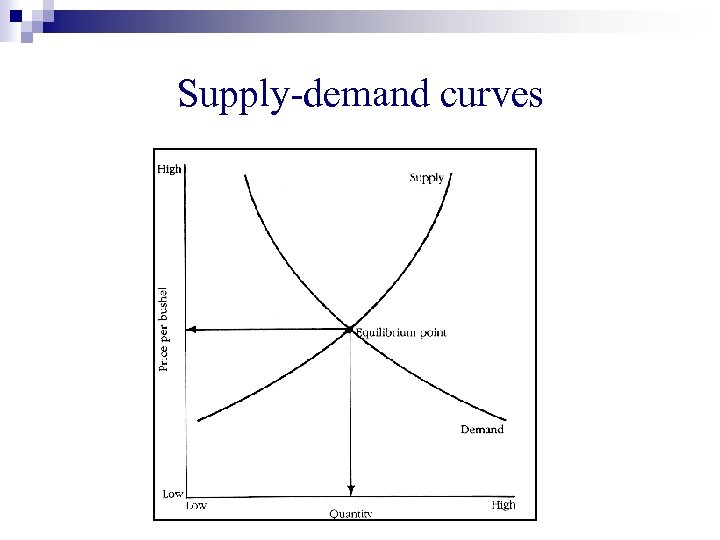Supply-demand curves

Leon Walras, 1874 n Pioneered general equilibrium theory

Irving Fisher, 1891 n First fundamental market model

Fisher’s Model, 1891 $ $$$$$ ¢ wine bread cheese n milk $$$$ People want to maximize happiness – assume Find prices linear utilities. s. t. market clears

Fisher’s Model n n n buyers, with specified money, m(i) for buyer i k goods (unit amount of each good) Linear utilities: is utility derived by i on obtaining one unit of j Total utility of i,

Fisher’s Model n n n buyers, with specified money, m(i) k goods (each unit amount, w. l. o. g. ) Linear utilities: is utility derived by i on obtaining one unit of j Total utility of i, Find prices s. t. market clears, i. e. , all goods sold, all money spent.

Arrow-Debreu Model, 1954 Exchange Economy n Second fundamental market model n Celebrated theorem in Mathematical Economics

Kenneth Arrow n Nobel Prize, 1972

Gerard Debreu n Nobel Prize, 1983

Arrow-Debreu Model n n agents, k goods

Arrow-Debreu Model n n agents, k goods n Each agent has: initial endowment of goods, & a utility function

Arrow-Debreu Model n n agents, k goods Each agent has: initial endowment of goods, & a utility function n Find market clearing prices, i. e. , prices s. t. if n ¨ Each agent sells all her goods ¨ Buys optimal bundle using this money ¨ No surplus or deficiency of any good

Utility function of agent i n n Continuous, monotonic and strictly concave n For any given prices and money m, there is a unique utility maximizing bundle for agent i.

Arrow-Debreu Model Agents: Buyers/sellers

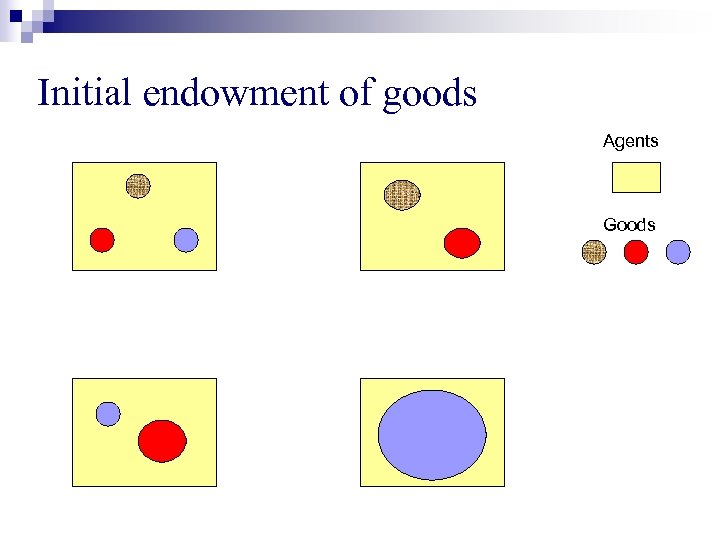Initial endowment of goods Agents Goods

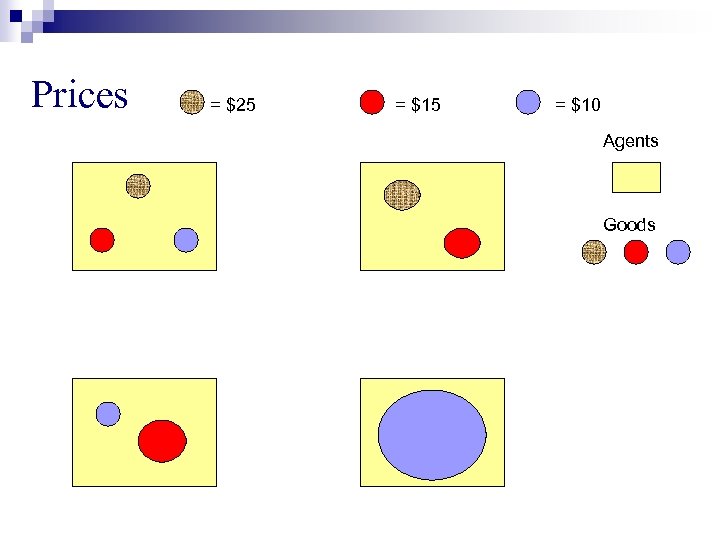Prices = $25 = $10 Agents Goods

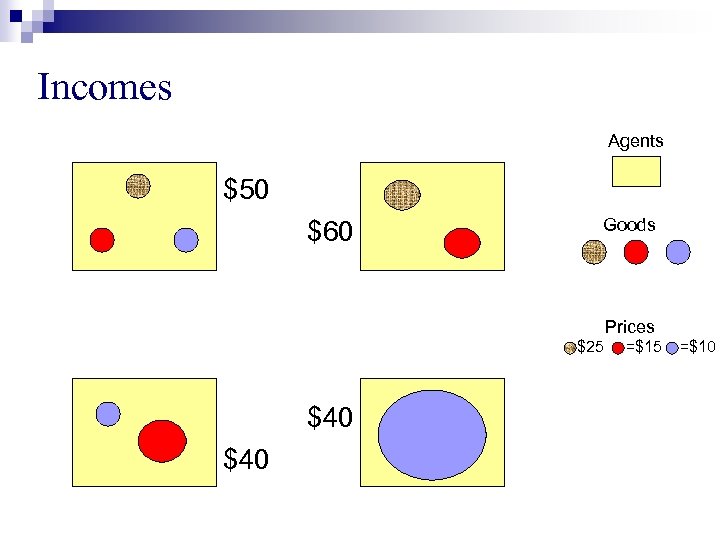Incomes Agents $50 $60 Goods Prices =$25 $40 =$15 =$10

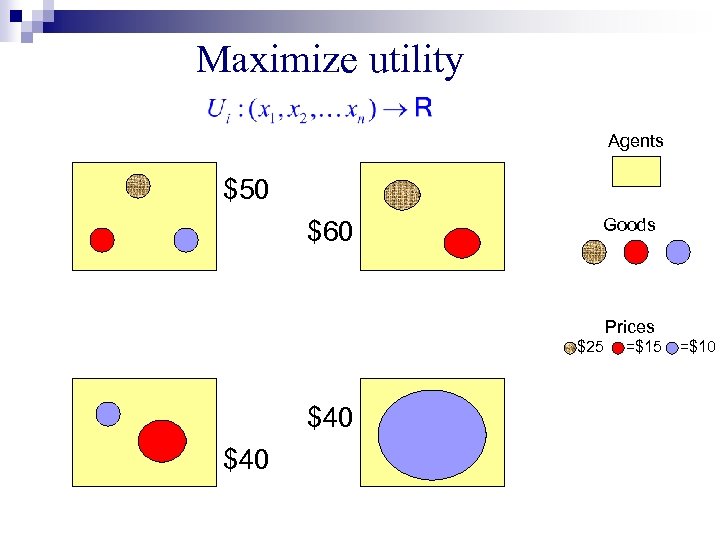Maximize utility Agents $50 $60 Goods Prices =$25 $40 =$15 =$10

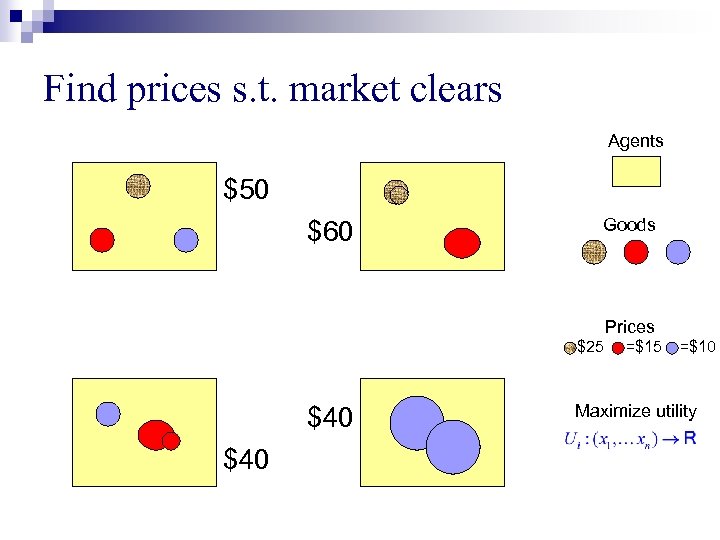Find prices s. t. market clears Agents $50 $60 Goods Prices =$25 $40 =$15 =$10 Maximize utility

n n n Observe: If p is market clearing prices, then so is any scaling of p Assume w. l. o. g. that sum of prices of k goods is 1. k-1 dimensional unit simplex

Arrow-Debreu Theorem n For continuous, monotonic, strictly concave utility functions, market clearing prices exist.

Proof n Uses Kakutani’s Fixed Point Theorem. ¨ Deep theorem in topology

Proof n Uses Kakutani’s Fixed Point Theorem. ¨ Deep n theorem in topology Will illustrate main idea via Brouwer’s Fixed Point Theorem (buggy proof!!)

n Let be a non-empty, compact, convex set n Continuous function n Then Brouwer’s Fixed Point Theorem

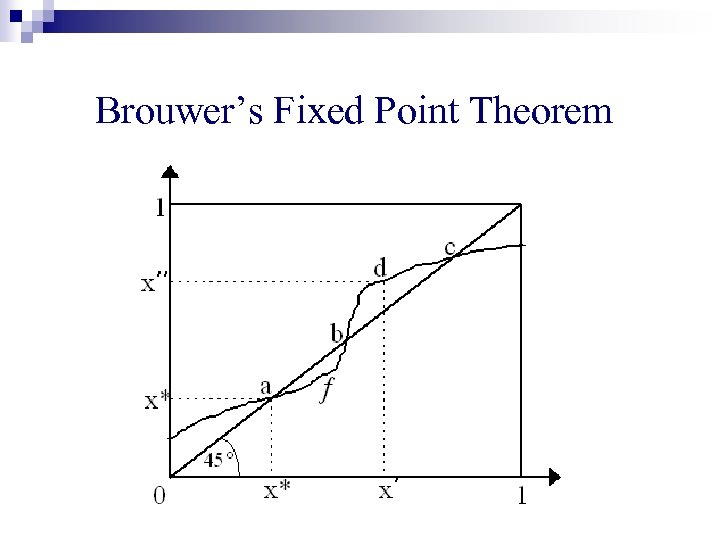Brouwer’s Fixed Point Theorem

Idea of proof n Will define continuous function n If p is not market clearing, f(p) tries to ‘correct’ this. n Therefore fixed points of f must be equilibrium prices.

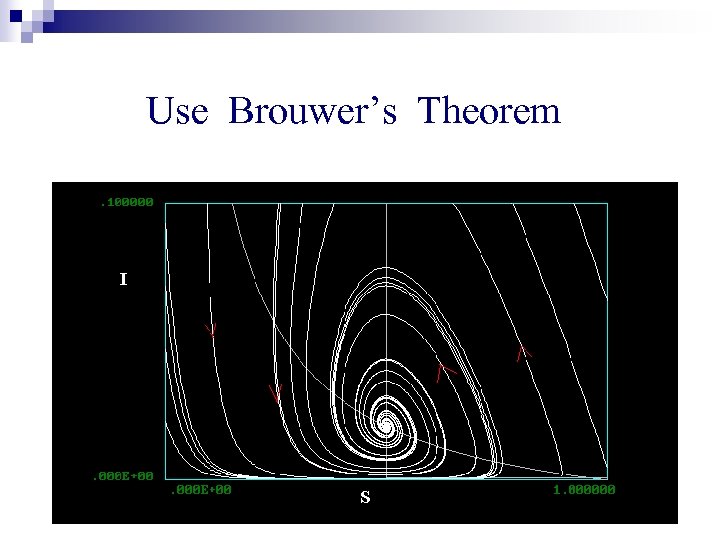Use Brouwer’s Theorem

When is p an equilibrium price? n s(j): total supply of good j. n B(i): unique optimal bundle which agent i wants to buy after selling her initial endowment at prices p. n d(j): total demand of good j.

When is p an equilibrium price? n s(j): total supply of good j. n B(i): unique optimal bundle which agent i wants to buy after selling her initial endowment at prices p. n d(j): total demand of good j. n For each good j: s(j) = d(j).

What if p is not an equilibrium price? n s(j) < d(j) => p(j) n s(j) > d(j) => p(j) n Also ensure

n Let n S(j) < d(j) => n S(j) > d(j) => n N is s. t.

=> is a cts. fn. of p => f is a cts. fn. of p

=> is a cts. fn. of p => f is a cts. fn. of p By Brouwer’s Theorem, equilibrium prices exist.

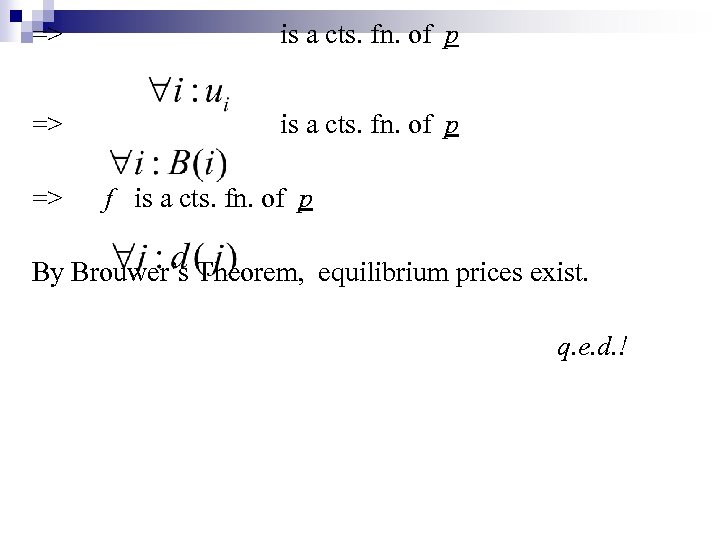=> is a cts. fn. of p => f is a cts. fn. of p By Brouwer’s Theorem, equilibrium prices exist. q. e. d. !

Kakutani’s Fixed Point Theorem n n convex, compact set non-empty, convex, upper hemi-continuous correspondence s. t.

Fisher reduces to Arrow-Debreu n Fisher: n buyers, k goods n AD: ¨ first n+1 agents n have money, utility for goods ¨ last agent has all goods, utility for money only.