Алгебра и начала анализа, 10 класс

Алгебра и начала анализа, 10 класс Графики тригонометрических функций

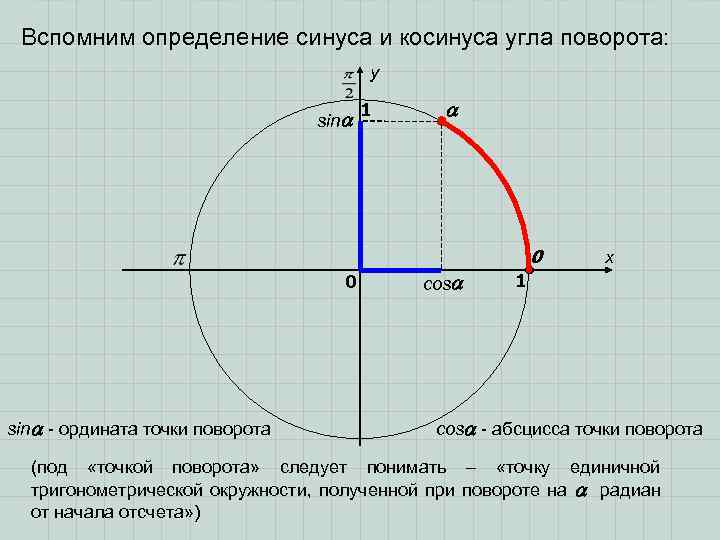
Вспомним определение синуса и косинуса угла поворота: y 1 sin 0 x 0 cos 1 sin - ордината точки поворота cos - абсцисса точки поворота (под «точкой поворота» следует понимать – «точку единичной тригонометрической окружности, полученной при повороте на радиан от начала отсчета» )

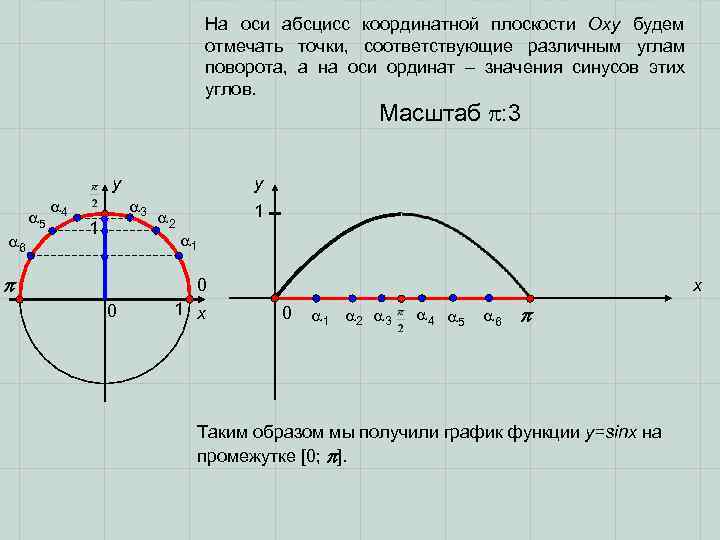
На оси абсцисс координатной плоскости Оху будем отмечать точки, соответствующие различным углам поворота, а на оси ординат – значения синусов этих углов. Масштаб : 3 y 4 3 1 5 2 1 6 1 0 x 0 1 x 0 1 2 3 4 5 6 Таким образом мы получили график функции y=sinx на промежутке [0; ].

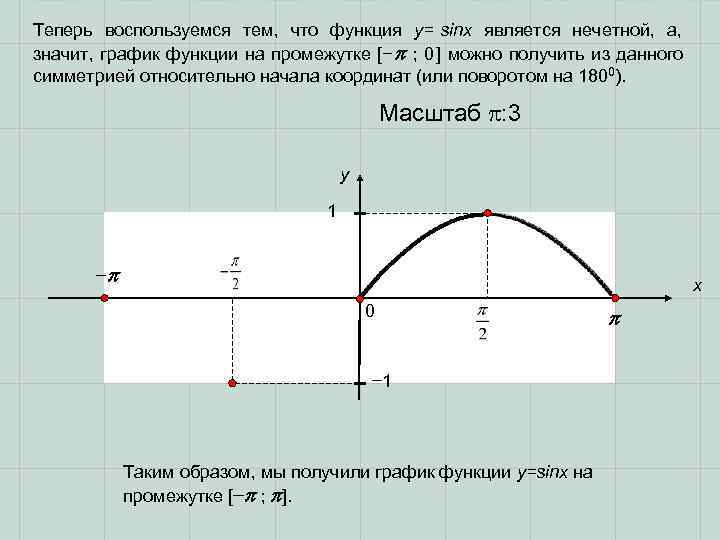
Теперь воспользуемся тем, что функция y= sinx является нечетной, а, значит, график функции на промежутке [− ; 0] можно получить из данного симметрией относительно начала координат (или поворотом на 1800). Масштаб : 3 y 1 − x 0 − 1 Таким образом, мы получили график функции y=sinx на промежутке [− ; ].

Напомним некоторые рациональные значения функции у=sinx на промежутке [− ; ]: y 1 0 x 0 1 − 1

На практике, для построения графика функции у= sinx на промежутке [0; ], сначала отмечают точки с координатами (0; 0), ( /6; 0, 5), ( /2; 1), ( 5 /6; 0, 5) и ( ; 0). Они образуют своеобразную «арку» , которая периодически (с периодом ) отображается симметрично оси Ох. y Масштаб : 3 1 0 x − 1 После этого используют свойство периодичности функции у=sinx. Так как наименьший положительный период функции y= sinx равен 2 , то изображенный участок графика можно параллельно переносить влево и вправо вдоль оси Ох на 2 n (n ) единичных отрезков. График функции y=sinx называется синусоидой.

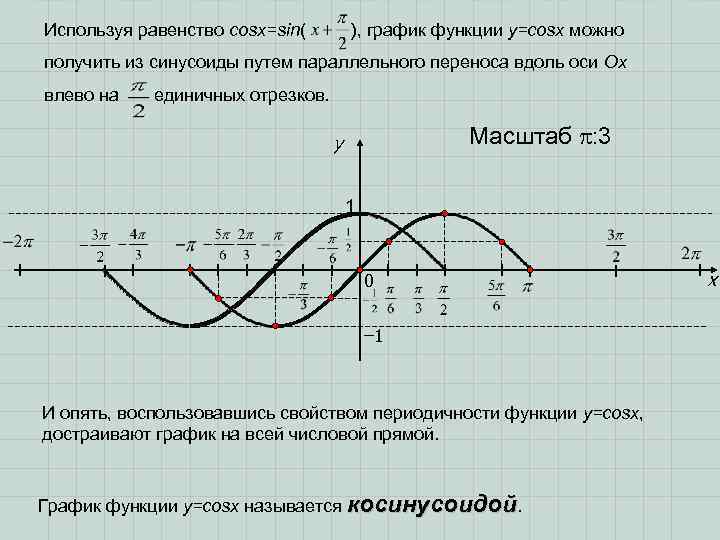
Используя равенство cosx=sin( ), график функции у=cosx можно получить из синусоиды путем параллельного переноса вдоль оси Ох влево на единичных отрезков. y Масштаб : 3 1 0 x − 1 И опять, воспользовавшись свойством периодичности функции y=cosx, достраивают график на всей числовой прямой. График функции y=cosx называется косинусоидой.

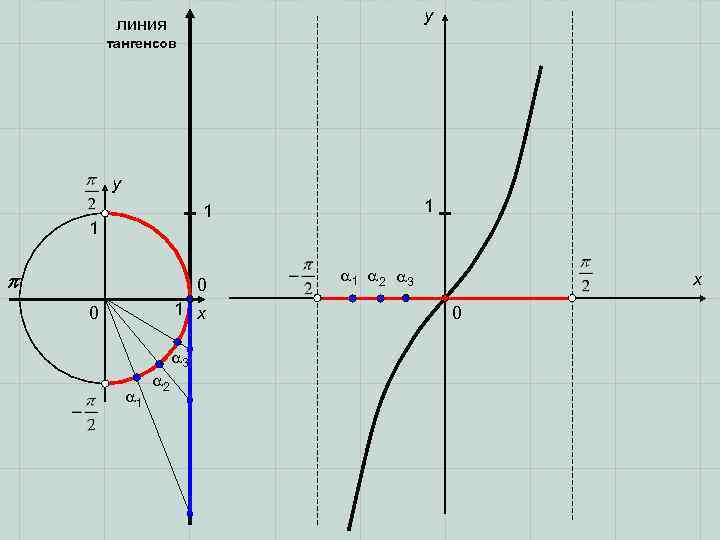
y линия тангенсов y 1 1 1 2 3 x 0 0 1 x 0 3 2 1

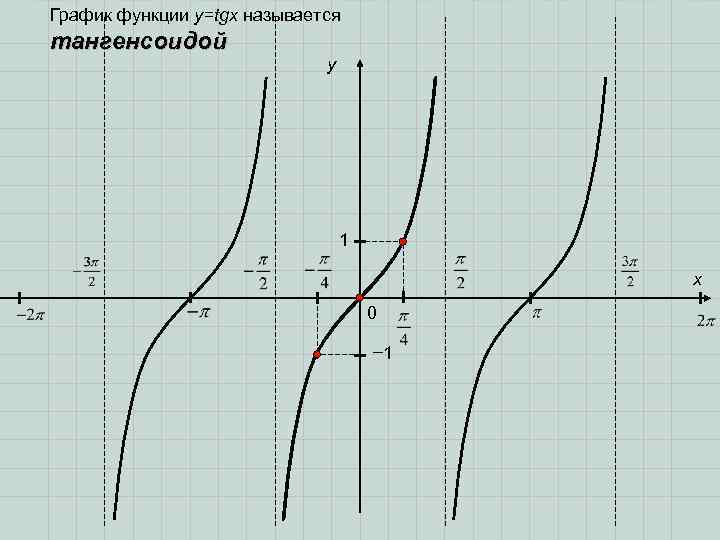
График функции y=tgx называется тангенсоидой y 1 x 0 − 1

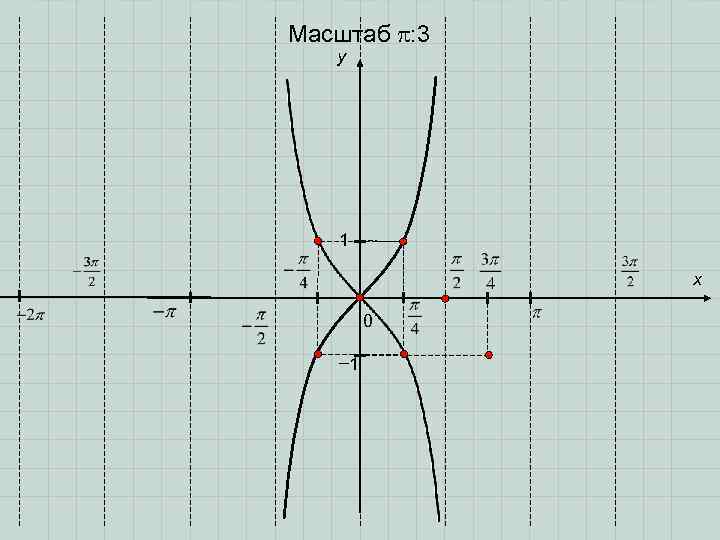
Масштаб : 3 y 1 x 0 − 1

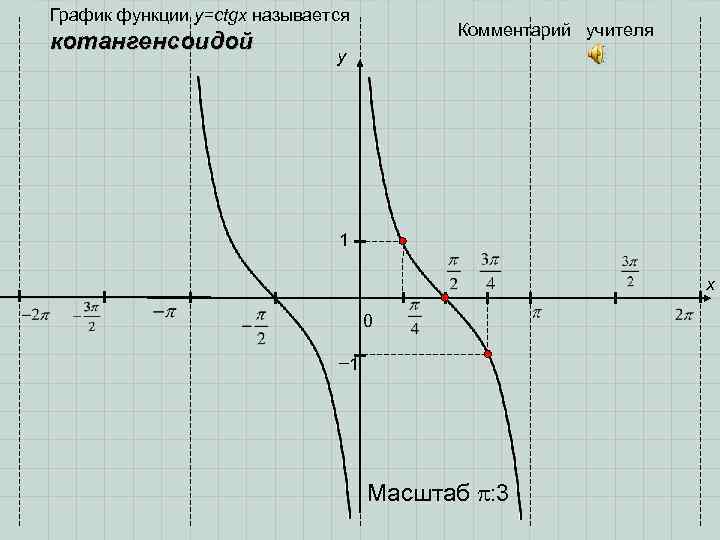
График функции y=ctgx называется Комментарий учителя котангенсоидой y 1 x 0 − 1 Масштаб : 3