Алгебра и геометрия.pptx
- Количество слайдов: 25

Алгебра и геометрия

Теорема Кронекера-Капелли. Теоре ма Кро некера — Капе лли — критерий совместности системы линейных алгебраических уравнений: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. Следствия • Количество главных переменных системы равно рангу системы. • Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

Определитель матрицы • Определителем матрицы является многочлен от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). • Определитель матрицы А обозначается как: det(A), |А| или Δ(A). • = ni=1(-1)i+1*ai 1 Mi 1 - вычисление определителя по первой строке.

Свойства определителей • • Определитель не меняется при транспонировании. Если одна из строк определителя состоит из нулей, то определитель равен нулю. Если в определителе переставить две строки, определитель поменяет знак. Определитель, содержащий две одинаковые строки, равен нулю. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k. Определитель, содержащий две пропорциональные строки, равен нулю. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j=1. . n), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом - из элементов cj. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.

Теорема (правило Крамера) • Система из n уравнений с n неизвестными в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам: xi = i/ • = det A, а i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.

Векторное пространство • 1. 2. 3. 4. 5. 6. 7. 8. Векторное пространство L(P) над полем P — это непустое множество L, на котором введены операции: сложения, то есть каждой паре элементов множества x, y L ставится в соответствие элемент того же множества, обозначаемый x + y L и умножения на скаляр (то есть элемент поля P), то есть любому элементу P и любому элементу x L ставится в соответствие единственный элемент из L(P), обозначаемый x L(P). При этом на операции накладываются следующие условия: коммутативность сложения ассоциативность сложения существование нейтрального элемента относительно сложения ( L, x+ = x для x L) существование противоположного элемента относительно сложения ( -x L, x+ (-x) = ) ассоциативность умножения на скаляр унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор дистрибутивность умножения на вектор относительно сложения скаляров дистрибутивность умножения на скаляр относительно сложения векторов

Простейшие свойства • Векторное пространство является абелевой группой по сложению. • Нейтральный элемент L является единственным, что вытекает из групповых свойств. • 0*x = для любого x L. • Для любого x L противоположный элемент -x L является единственным, что вытекает из групповых свойств. • (-1)*x = -x для любого x L. • (- )*x = *(-x) = -( x) для любых P и x L. • * = для любого P.

Линейная зависимость и независимость векторов • ОПРЕДЕЛЕНИЕ. Говорят, что векторы a 1, a 2, …, ak линейно зависимы, если существуют числа 1, 2, …, k, не все равные нулю и такие, что линейная комбинация 1*a 1 + 2*a 2 + … + k*ak равна нулевому элементу o линейного пространства L. • Если же равенство 1*a 1 + 2*a 2 + … + k*ak = o возможно только при условии 1 = 2 = 3 = … k = 0, то векторы a 1, a 2, …, ak называют линейно независимыми. • Векторы a 1, a 2, …, ak линейно зависимы тогда и только тогда, когда хотя бы один из них линейно выражается через оставшиеся.

Базис • • Максимальная линейно независимая система векторов линейного пространства называется базисом этого линейного пространства. Иначе говоря, векторы e 1, e 2, …, en L образуют базис в линейном пространстве если выполняются два условия: 1) e 1, e 2, …, en – линейно независимы; 2) e 1, e 2, …, en, a – линейно зависимы для любого вектора a из L. Очевидно, что в линейном пространстве существует не единственный базис. Но справедлива следующая теорема: Любые два базиса линейного пространства состоят из одного и того же числа векторов. Замечание. Хотя в качестве базиса на плоскости (в пространстве) можно взять любые два неколлинеарных (любые три некомпланарных) вектора, на практике предпочитают работать с декартовым прямоугольным базисом i, j ( i, j, k). Это единичные векторы, которые сонаправлены координатным осям Ox и Oy соответственно (сонаправлены координатным осям Ox, Oy и Oz соответственно). Каждый вектор линейного пространства линейно выражается через любой его базис, причем единственным образом.

Базис • Тройка векторов e 1, e 2, e 3 называется базисом в трехмерном пространстве геометрических векторов V 3, если любой вектор x V 3 может быть единственным образом представлен в виде x = α · a + β · b + γ · c, • где α, β, γ — некоторые числа, называемые координатами вектора x в базисе e 1, e 2, e 3.

Линейные операторы • • В векторном пространстве R задан оператор, или преобразование, A^, если каждому вектору x R поставлен в соответствие определенный вектор A^ (x), или A^ x R. Оператор (преобразование) A^ называется линейным, если для любых двух векторов x и y из R и произвольного числа A^ (x + y) = A^ x + A^ y A^ - обозначение оператора A^ ( *x) = *A^ x Вектор A^ x называется образом вектора x, а вектор x – прообразом вектора A^ x при преобразовании A^. Выберем в пространстве R базис e 1, e 2, …, en. Тогда x = x 1 e 1 + x 2 e 2 + … + xnen. Кроме того, так как A^ ei (i = 1. . n) – это тоже вектор из R, то A^ ei можно разложить по базису e 1, e 2, …, en. Каждому линейному оператору A^ в базисе e 1, e 2, …, en отвечает матрица: a 11 a 12 … a 1 n A = a 21 a 22 … a 2 n … an 1 an 2 … ann i-й столбец которой образован координатами разложения вектора A^ ei по базису e 1, e 2, . . , en; при этом коэффициенты разложений координаты вектора A^ x по координатам вектора x образуют строки матрицы A.

Свойства линейных операторов • Легко видеть, что A*0 = 0 • При этом, если A^ x = 0 только при x = 0, то оператор называется невырожденным; если же найдется такой вектор x 0, что A^ x=0, то оператор A^ – вырожденный. • Для существования ненулевого решения этой системы и, значит, для существования ненулевого вектора x = x 1 e 1 + x 2 e 2 + … + xnen такого, что A^ x = 0, необходимо и достаточно, чтобы определитель матрицы A был равен нулю, следовательно, для того, чтобы оператор A^ был невырожденным, необходимо и достаточно, чтобы определитель матрицы A этого оператора (в любом базисе) был отличен от нуля.

Связь между матрицами одного и того же линейного оператора в разных базисах • Если в базисе e 1, e 2, …, en линейный оператор A^ имеет матрицу A, в базисе e 1’, e 2’, …, en’ - матрицу B, а S - матрица перехода от первого базиса ко второму, то B = S-1 AS

Собственные векторы и собственные значения линейного оператора • Пусть A^ : Xn → Xn — линейный оператор. • Вещественное число λ называется собственным значением оператора A^, если существует ненулевой вектор x Xn такой, что A^ x = λ x • Вектор x называется собственным вектором оператора A^, соответствующим собственному значению λ. • Замечание. Из определения следует, что образ собственного вектора коллинеарен его прообразу.

Характеристическое уравнение • Собственные значения λ i являются корнями характеристического уравнения det(A −λE) = 0. • Многочлен P(λ) = − det(A − λE), из левой части характеристического уравнения, называется характеристическим многочленом матрицы A. • Характеристический многочлен P(λ) = − det(A − λE) — многочлен степени n относительно λ: P(λ) = λn − an-1λn-1+ an-2λn-2+. . . + (− 1)na 0 • Характеристическим многочленом линейного оператора A^ называют характеристический многочлен его матрицы A, записанной в некотором базисе, а характеристическим уравнением этого оператора – характеристическое уравнение матрицы A.

Прямая на плоскости. Уравнение прямой с угловым коэффициентом. • Прямая, заданная уравнением y = kx + b, параллельна прямой, описанной уравнением y = kx. Коэффициент b есть величина отрезка, отсекаемого прямой y = kx + b на оси Oy. Эта величина может быть как положительной, так и отрицательной. Для того, чтобы построить график прямой y = kx + b, зная график прямой y=kx, надо прямую y=kx параллельно поднять на величину b относительно начала координат, если b>0. Если же величина b отрицательная, тогда прямую y=kx надо параллельно опустить на величину b относительно начала координат. • Коэффициент k называется угловым коэффициентом. Равен он тангенсу угла наклона, образуемого прямой с положительным направлением оси Ox, т. е. k = tg.

Общее уравнение прямой на плоскости • Линейное уравнение вида Ax + By + C = 0 называется общим уравнением прямой на плоскости. • Если коэффициент C = 0, то прямая, уравнение которой в этом случае записывается Ax + By = 0, проходит через начало координат. • Важную роль выполняют коэффициенты A, B. Вектор n(A, B), координатами которого являются эти числа, называется нормальным вектором прямой, заданной уравнением Ax + By + C = 0. • Следует обратить внимание на тот факт, что A - это проекция нормального вектора n(A, B) на ось Ox, B - это проекция нормального вектора n(A, B) на ось Oy. • Вектор n(A, B), начало которого совпадает с началом координат, задает общее расположение прямой на плоскости: искомая прямая перпендикулярна вектору n(A, B).

Уравнение прямой, проходящей через точку, с заданным угловым коэффициентом • На плоскости дана точка M 0(x 0, y 0). Прямая, угловой коэффициент k которой задан, проходит через эту точку. Уравнение ее имеет вид: y – y 0 = k(x – x 0) • M(x, y) – точка, находящаяся на той же прямой (произвольная).

Уравнение прямой, проходящей через две заданные точки • На плоскости даны две точки M 1(x 1, y 1) и M 2(x 2, y 2). Уравнение прямой, проходящей через эти точки, очень легко написать. На прямой возьмем текущую, т. е. любую, точку M(x, y). Построим два вектора M 1 M(x -x 1, y-y 1) и M 1 M 2(x 2 -x 1, y 2 -y 1). По построению эти векторы коллинеарны. Условие коллинерности – это пропорциональность одноименных координат векторов: (x-x 1)/(x 2 -x 1) = (y-y 1)/(y 2 -y 1) • Это и есть искомое уравнение. • Угловой коэффициент k = (y 2 -y 1)/(x 2 -x 1)

Уравнение прямой в «отрезках» • Предположим, прямая задана общим уравнением Ax + By + C = 0. Полагаем, что в уравнении коэффициент C 0. В противном случае задача упрощается, так как прямая проходит через начало координат. Ax + By = -C Ax/(-C) + By/(-C) = 1 x/(-C/A) + y/(-C/B) = 1 x/a + y/b =1 • Здесь введены обозначения: a = -C/A, b = -C/B. • Полученное уравнение x/a + y/b =1 и есть искомое уравнение прямой в «отрезках» .
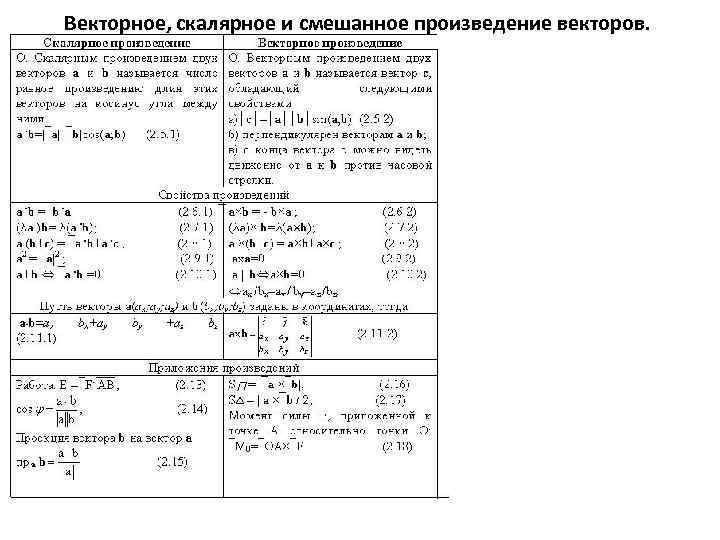
Векторное, скалярное и смешанное произведение векторов.


Уравнение плоскости, проходящей через три заданных точки. Нормальное уравнение плоскости.


Алгебра и геометрия.pptx