Глава 4. Аналитическая геометрия на плоскости.pptx
- Количество слайдов: 95

Алгебра и геометрия Глава 4. Аналитическая геометрия на плоскости Одияко Наталья Николаевна, доцент кафедры математики и моделирования Ауд. 1602, тел. 240 -40 -65 Natalya. Odiyako@vvsu. ru

Содержание лекции

Ключевые понятия

Основные определения • Линия на плоскости есть множество точек, обладающих некоторыми геометрическими свойствами, исключительно им присущими.

• Уравнением линии (кривой) на плоскости OXY называется уравнение, которому удовлетворяют координаты X и Y каждой точки данной линии и не удовлетворяют координаты точек, не лежащих на этой линии.

• Точка M (x; y) передвигается по линии; её координаты x и y, изменяясь, удовлетворяют уравнению линии, поэтому т. M называется текущей точкой линии, а её координаты – текущими координатами точки линии.

• Составить уравнение линии – значит составить уравнение, связывающее координаты текущей точки линии.

• Основные задачи аналитической геометрии: 1) Дана линия, рассматриваемая как множество точек. Составить уравнение линии; 2) Дано уравнение некоторой линии. Изучить по этому уравнению её геометрические свойства (определить форму и расположение).

• Линия называется линией или кривой n-го порядка, если она определяется уравнением n-ой степени относительно текущих прямоугольных координат.

•

Прямая линия • .

• , ,
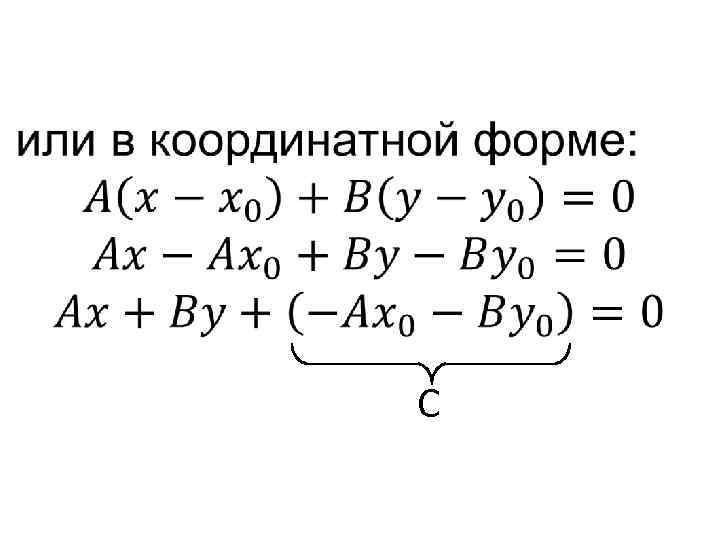
• C

•

• Можно доказать, что любое линейное уравнение определяет прямую. • Геометрический смысл чисел A и B: эти числа являются координатами вектора, перпендикулярного прямой. Этот вектор называется нормалью прямой.

•

•

Если x=0, то y=b; если y=0, то x=a; т. е. прямая проходит через точки (a; 0), (0; b); a и b – «отрезки» , отсекаемые прямой на осях координат.

•

•

•

•

• Параметрические уравнения прямой. Т. к. т. M (x; y) – текущая точка прямой, то её координаты удовлетворяют уравнению прямой, при этом будет сохраняться равенство 2 -х отношений в каноническом уравнении прямой.
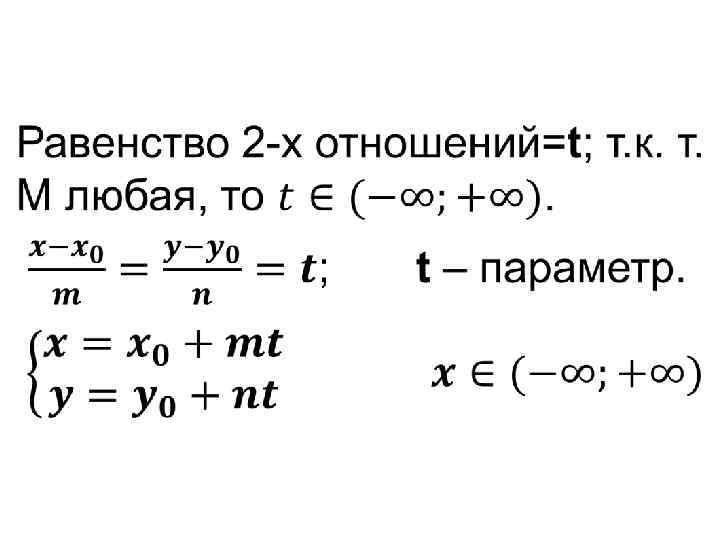
•

•

λ • M

•

• λ M

•

•
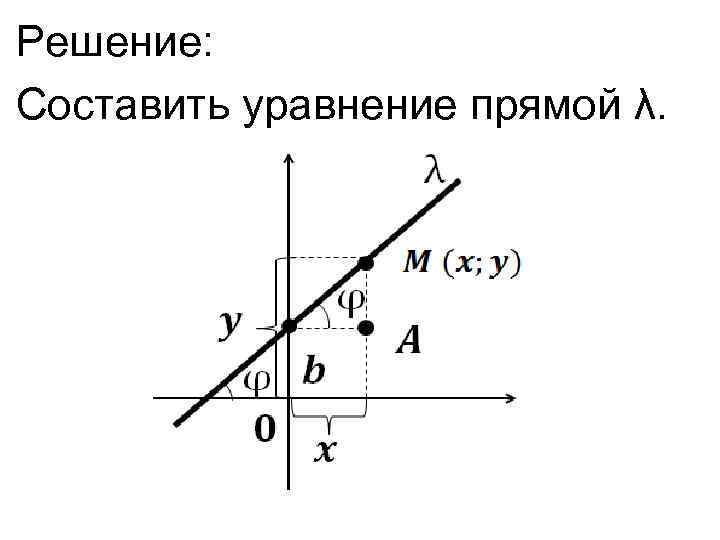
Решение: Составить уравнение прямой λ.

•
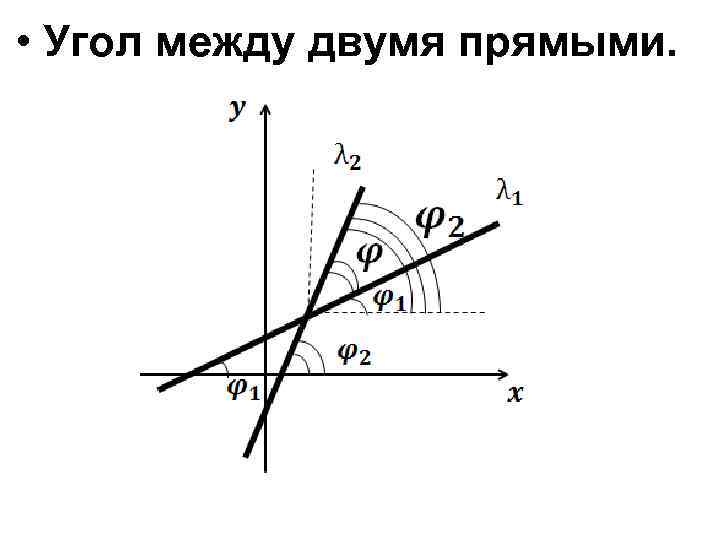
• Угол между двумя прямыми.

•

•

•
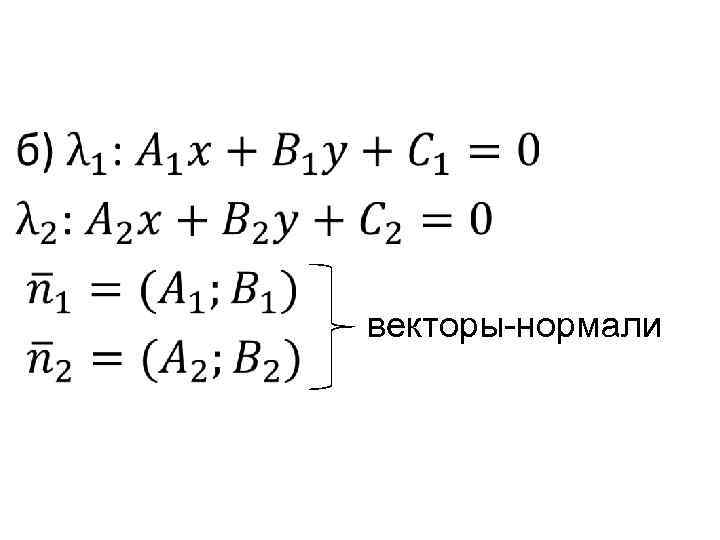
• векторы-нормали

•

•

•

Решение: Составим уравнение, связывающее координаты текущей точки прямой.

•

•
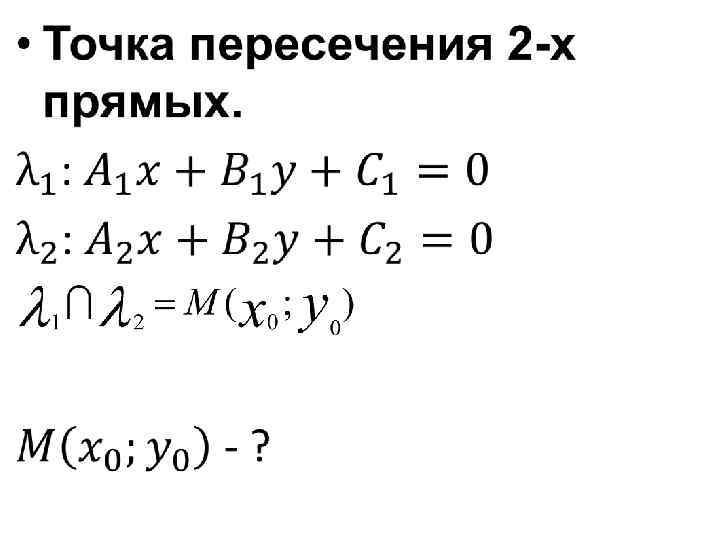
•
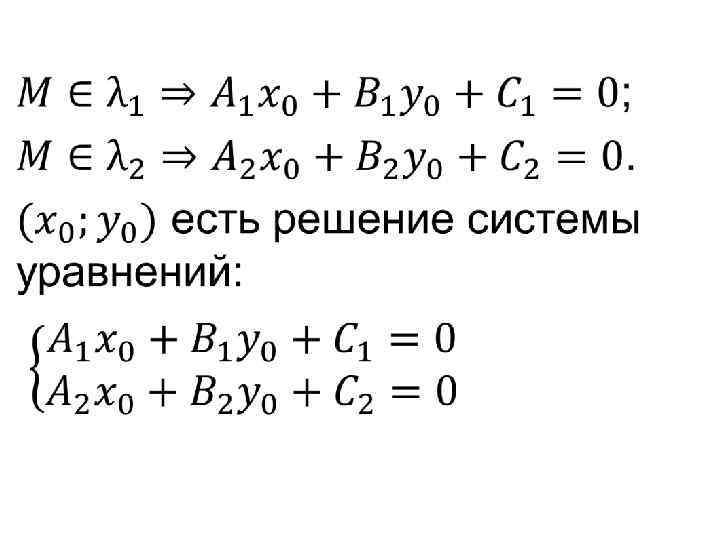
•

• Взаимное расположение 2 -х прямых. Если прямые пересекаются, то система уравнений имеет единственное решение. Если прямые параллельны, то система не имеет решений. Если прямые совпадают, то система имеет бесконечно много решений.

•

•

•

• Кривые 2 -го порядка.

•
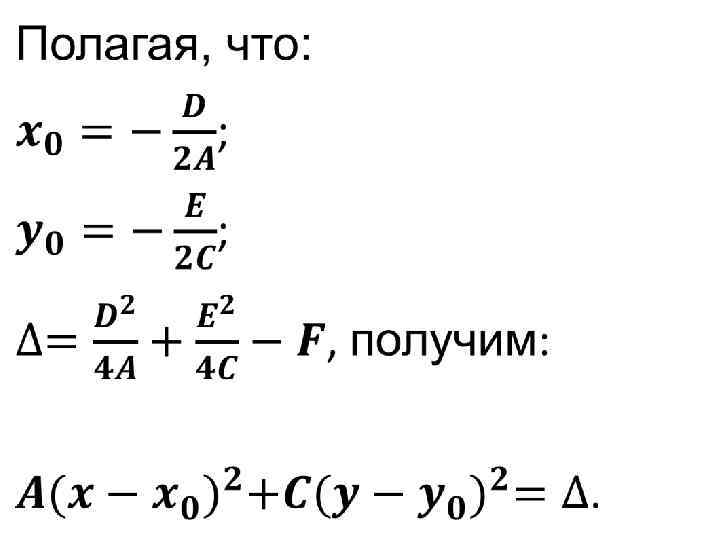
•

•

• Кривые эллиптического типа. Кривая 2 -го порядка называется эллипсом, если коэф. A и C имеют одинаковые знаки. Условимся, что A и C > 0 (иначе умножим обе части уравнения на -1).

•

•

Геометрическое свойство эллипса: Кривая 2 -го порядка является эллипсом, если представляет собой геометрическое место точек плоскости, сумма расстояний от каждой из которых до 2 -х данных точек этой плоскости, называемых фокусами, есть величина постоянная (её обозначают 2 a), причём эта постоянная больше расстояния между фокусами.

Чертёж эллипса, соответствующего каноническому уравнению:


•

Геометрическое свойство окружности: геометрическое место точек в плоскости, равноудалённых от одной точки, называется центром окружности.

•

•

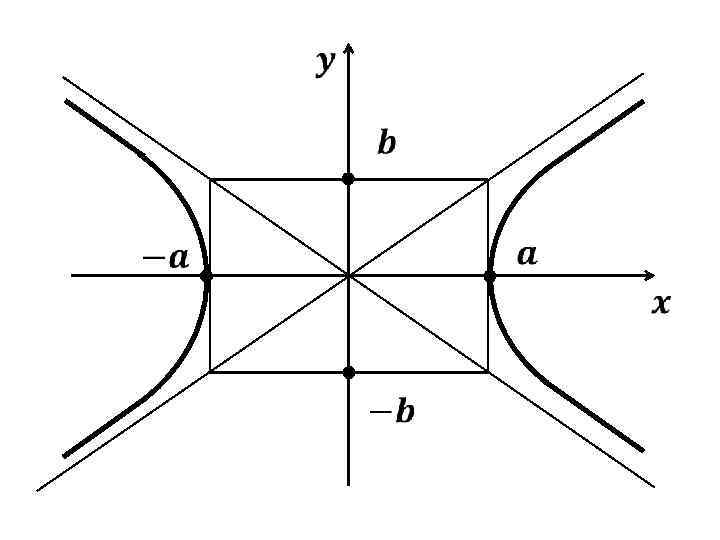
Ось Ox – действительная ось (a – действительная полуось в этом случае), ветви гиперболы направлены вдоль оси Ox. Ось Oy – мнимая ось (b – мнимая полуось в этом случае).

•
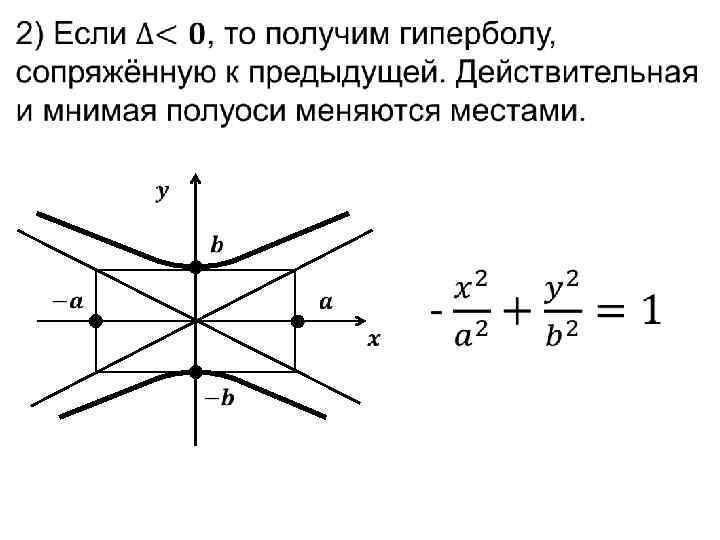
•
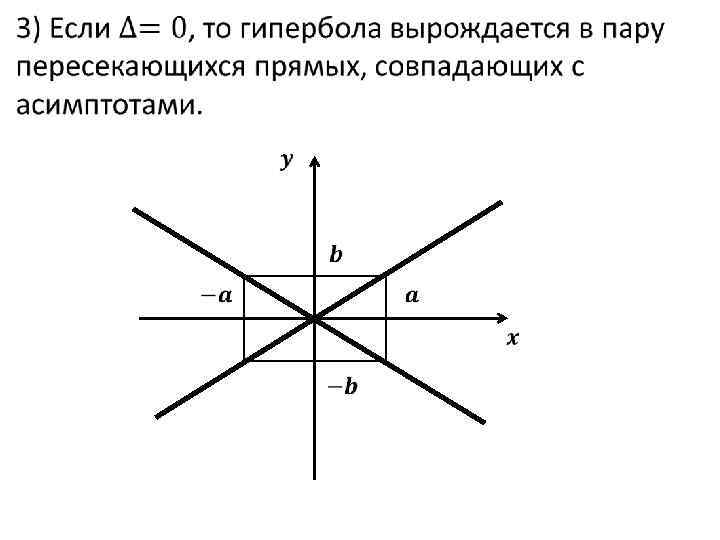
•

•

• Кривые параболического типа. Кривая 2 -го порядка называется нецентральной, если она или не имеет центра симметрии, или же имеет бесконечно много центров симметрии.

•

•
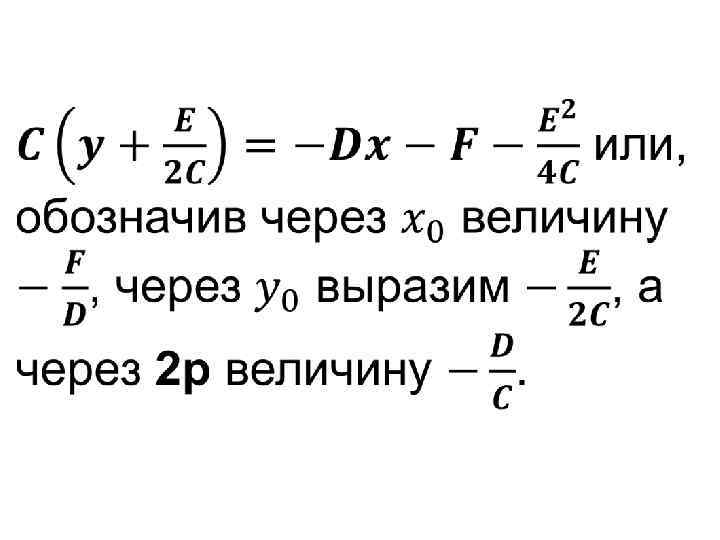
•

•

•

•

• Применение кривых 2 -го порядка к решению экономических задач. Задача 1. 2 предприятия, находящиеся одно от другого на расстоянии 100 км, производят некое изделие, причём фабрично-заводская цена изделия на обоих предприятиях одинакова и равна p. Пусть транспортные расходы на перевозку от предприятия A до потребителя равны 9 руб. /км, а от предприятия B – 3 руб. /км. Как будет разделён рынок сбыта, если расходы потребителя должны быть одинаковы?
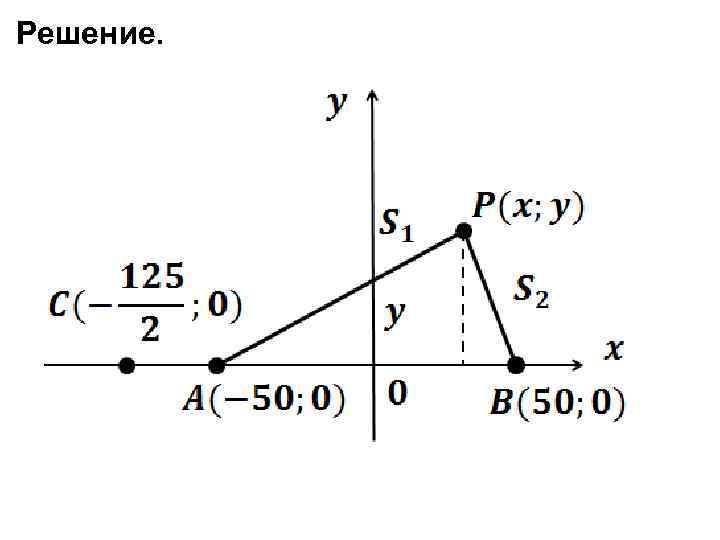
Решение.

•

•

•

•

•

•

•

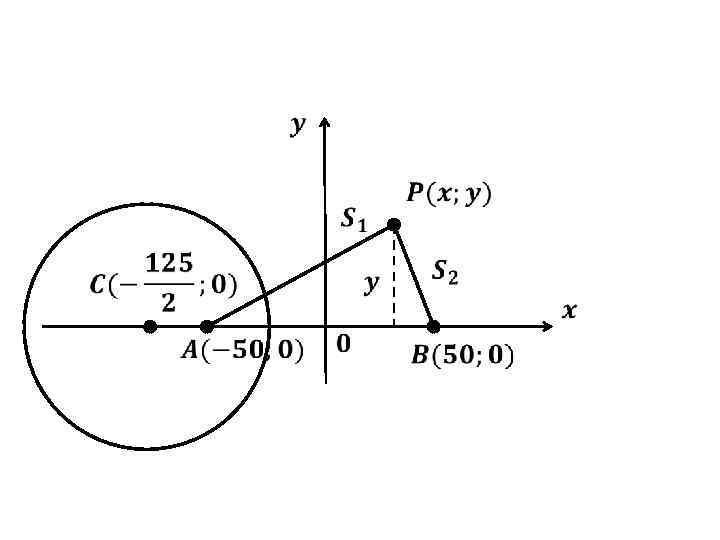
Для потребителя, находящегося на этой окружности, расходы на приобретение изделия одинаковы. Для потребителей, находящихся вне окружности, расходы ниже на предприятии B, а для потребителей, находящихся внутри окружности, - на предприятии A.

• Геометрические свойства гиперболы и параболы. Геометрическое свойство гиперболы: Гипербола есть геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до 2 -х данных точек этой плоскости, называемых фокусами, есть величина постоянная (равная 2 a) и меньшая, чем расстояние между фокусами.

•

Геометрическое свойство параболы: Парабола – множество точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса до директрисы равно параметру p, взятому со знаком «+» .

•

•

Вопросы и задания для самопроверки

Рекомендуемая литература

Использование материалов презентации Использование данной презентации, может осуществляться только при условии соблюдения требований законов РФ об авторском праве и интеллектуальной собственности, а также с учетом требований настоящего Заявления. Презентация является собственностью авторов. Разрешается распечатывать копию любой части презентации для личного некоммерческого использования, однако не допускается распечатывать какую-либо часть презентации с любой иной целью или по каким-либо причинам вносить изменения в любую часть презентации. Использование любой части презентации в другом произведении, как в печатной, электронной, так и иной форме, а также использование любой части презентации в другой презентации посредством ссылки или иным образом допускается только после получения письменного согласия авторов.
Глава 4. Аналитическая геометрия на плоскости.pptx