Алгебра и геометрия Глава 2 Элементы теории матрицы

Алгебра и геометрия Глава 2. Элементы теории матрицы Одияко Наталья Николаевна, доцент кафедры математики и моделирования Ауд. 1602, тел. 240 -40 -65 Natalya. Odiyako@vvsu. ru

Содержание лекции

Ключевые понятия

Основные понятия и определения. Системы линейных алгебраических уравнений (СЛАУ) • Систему m линейных уравнений с n неизвестными будем записывать в следующем виде:

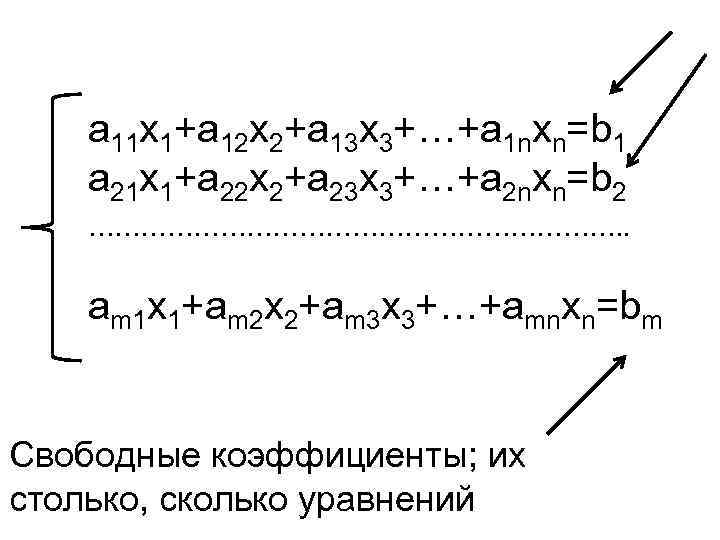
a 11 x 1+a 12 x 2+a 13 x 3+…+a 1 nxn=b 1 a 21 x 1+a 22 x 2+a 23 x 3+…+a 2 nxn=b 2 …………………………. . am 1 x 1+am 2 x 2+am 3 x 3+…+amnxn=bm Свободные коэффициенты; их столько, сколько уравнений

Здесь: • x 1, x 2, …, xn – неизвестные величины; • aij (i=1, 2, …, m; j=1, 2, …, n) – числа, называемые коэффициентами системы (первый индекс фиксирует номер уравнения, второй – номер неизвестной); • b 1, b 2, …, bm – числа, называемые свободными членами.

• Решением системы будем называть упорядоченный набор чисел x 1= c 1, x 2=c 2, …, xn=cn, обращающий каждое уравнение системы в верное равенство. • Решить систему – значит найти все её решения или доказать, что решений нет.

• Система, имеющая решение, называется совместной. • Если система имеет только одно решение, то она называется определённой.

• Система, имеющая более чем одно решение, называется неопределённой (совместной и неопределённой). • Если система не имеет решений, то она называется несовместной.

• Система, у которой все свободные члены равны нулю (b 1=b 2=…=bm=0), называется однородной. • Однородная система всегда совместна, т. к. набор из m нулей удовлетворяет любому уравнению такой системы.

• Нулевое решение однородной системы называется тривиальным (простым).

• Если число уравнений системы совпадает с числом неизвестных (m=n), то система называется квадратной. • Две системы, множества решений которых совпадают, называются эквивалентными или равносильными.

• Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием.

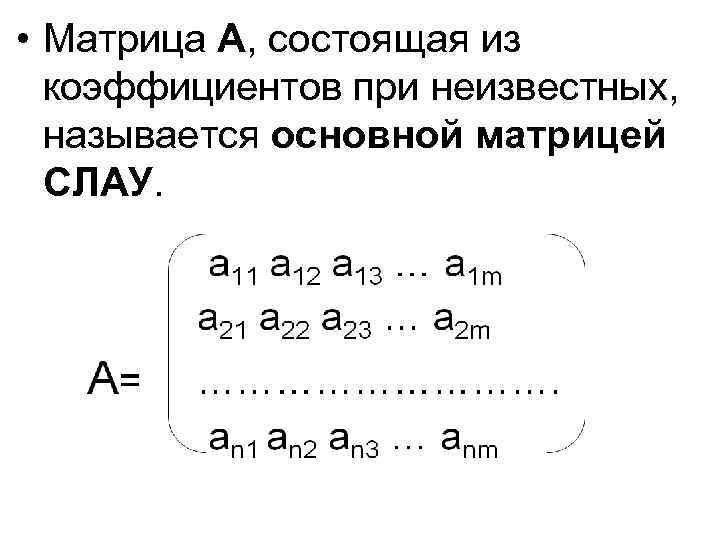
• Матрица A, состоящая из коэффициентов при неизвестных, называется основной матрицей СЛАУ.

• Матрица, состоящая из коэффициентов при неизвестных, в которой в качестве последнего столбца записан столбец свободных коэффициентов, называется расширенной матрицей СЛАУ. А *= a 11 a 12 a 13 … a 1 n a 21 a 22 a 23 … a 2 n b 1 b 2 ………………. …… am 1 am 2 am 3 … amn bm

•

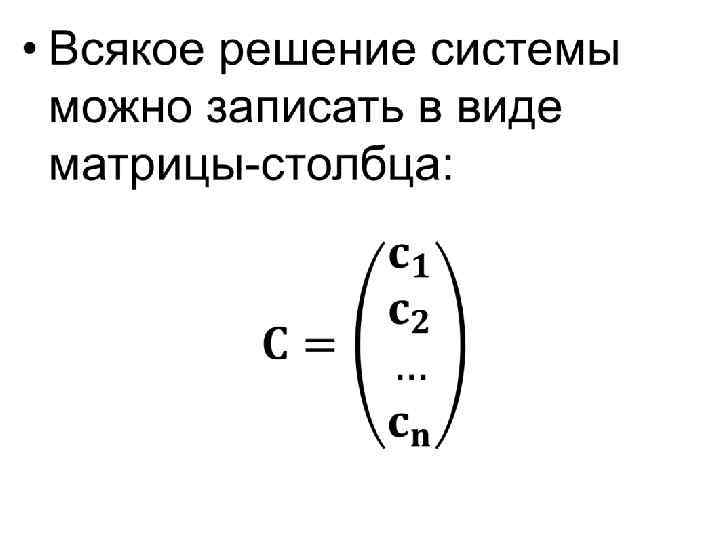
Теорема о совместности СЛАУ • Теорема Кронекера. Капелли. Для того чтобы СЛАУ была совместна, необходимо и достаточно, чтобы ранг A равнялся рангу A*.

• Если система совместна и: 1)ранг системы равен числу неизвестных (r(A)=m), то система имеет единственное решение; 2)ранг системы меньше числа неизвестных (r(A)<m), то система имеет бесчисленное множество решений.

Методы решения СЛАУ 1)матричный метод; 2)метод Гаусса; 3)метод Крамера.

• Матричный метод решения СЛАУ запишем в виде A∙X=B. Если det. A≠ 0 (А невырожденная), то для матрицы A существует обратная матрица A-1 (рассматриваем квадратные СЛАУ).

Умножим обе части СЛАУ слева -1: на A -1∙A∙X= A -1∙B A E∙X= A-1∙B X= -1∙B A Получим решение СЛАУ в матричном виде.

• Метод Крамера (для квадратных систем). Если в СЛАУ n=m и det. A≠ 0, то СЛАУ имеет единственное решение: ; ; … ;

где Δ 1, Δ 2, …, Δn получены из определителя матрицы системы заменой последовательно 1 -го, 2 -го, …, n-го столбцов на столбец свободных коэффициентов.

Если det. A=0 и все Δ=0, то СЛАУ имеет множество решений, и применяется метод Гаусса. Если det. A=0, а хотя бы 1 из Δ≠ 0, то СЛАУ несовместна.

• Метод Гаусса (метод исключения неизвестных). Метод основан на последовательном исключении неизвестных из уравнений. Если в 1 -ом уравнении a 11≠ 0, то с помощью элементарных преобразований x 1 исключают из оставшихся уравнений (кроме первого). Если в новой системе a 22≠ 0, то во всех уравнениях, начиная с 3 -го, исключаются x 2, и так далее, пока не перейдём к треугольному виду.

Если в процессе приведения системы к треугольному виду появятся нулевые уравнения (равенства вида 0=0), то их отбрасывают. Если же появится уравнение вида 0=b, а b≠ 0, то данная система несовместна. Последнее возможно, когда ранг A ≠ рангу A*.

Вопросы и задания для самопроверки

Рекомендуемая литература

Использование материалов презентации Использование данной презентации, может осуществляться только при условии соблюдения требований законов РФ об авторском праве и интеллектуальной собственности, а также с учетом требований настоящего Заявления. Презентация является собственностью авторов. Разрешается распечатывать копию любой части презентации для личного некоммерческого использования, однако не допускается распечатывать какую-либо часть презентации с любой иной целью или по каким-либо причинам вносить изменения в любую часть презентации. Использование любой части презентации в другом произведении, как в печатной, электронной, так и иной форме, а также использование любой части презентации в другой презентации посредством ссылки или иным образом допускается только после получения письменного согласия авторов.