7d56ebe935b9689c420c52356b9711b7.ppt
- Количество слайдов: 32

АЛГЕБРА 7 Глава IV. МНОГОЧЛЕНЫ Выполнила: учитель математики МОУ Центр образования Сормовского района Столярова Елена Геннадьевна

ОГЛАВЛЕНИЕ 1. Пояснительная записка 2. Цели и задачи раздела 3. Психолого-педагогическое объяснение 4. Ожидаемые результаты освоения раздела программы 5. Обоснование используемых технологий, методов, форм организации деятельности учащихся 6. Система знаний и система деятельности 7. Поурочное планирование по разделу 8. Разработка урока 9. Дидактические материалы 10. Список литературы

1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА а) актуальность Раздел содержит - теоретическую и практическую части по алгебре; - презентацию к уроку по теме «Сложение и вычитание многочленов» ; - информационные материалы; - дидактические материалы по теме «Многочлены» . б) принципы отбора содержания образования - овладение системой математических знаний и умений, применяемых в практической деятельности; - интеллектуальное развитие учащихся; - формирование представлений о методах математики как средства моделирования явлений и процессов; - формирование представлений о роли математики в развитии цивилизации и культуры

2. ЦЕЛИ И ЗАДАЧИ Основная цель – выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители Задачи: образовательные -научить учащихся складывать, вычитать и умножать многочлены; -научить применять действия с многочленами в заданиях на преобразования алгебраических выражений; -формирование умения разложения многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки; -уметь использовать рассматриваемые преобразования при решении уравнений и доказательстве тождеств; - продолжить работу по формированию умения решать задачи методом составления уравнений

Развивающие: 1. учащиеся должны уметь раскрывать скобки и приводить подобные члены приведении суммы, разности и произведения многочленов к многочлену стандартного вида; 2. учащиеся должны продолжить развитие умения и навыков установления связей между компонентами и результатами этих действий; 3. формирование умения раскладывать многочлен на множители; 4. уметь применять разложения многочлена на множители для рационализации вычислений, решения уравнений, доказательства делимости чисел. Коррекционно - развивающие: 1. научить применению полученных на уроках знаний в новых ситуациях; 2. развитие устной математической речи учащихся средствами предмета; 3. способствовать развитию познавательной активности: мыслительных операций (анализа, синтеза, ассоциативного мышления), воображения, образного восприятия окружающего мира; 4. продолжить формирование вычислительных навыков учащихся; Воспитательные: 1. развивать интерес к предмету; 2. развивать навык правильно оформлять письменные работы; 3. продолжить формирование правильной самооценки.

3. Психолого-педагогическое объяснение специфики восприятия и освоения учебного материала учащимися. Психологической особенностью детей Центра образования является -низкий уровень логического мышления, -низкий уровень развития смысловой памяти. Приемы на развитие памяти: - запоминание путем повторения информации; - осмысленное запоминание; - эмоциональное запоминание. Виды памяти: - наглядно-образная; - словесно-логическая; - эмоциональная. Развитие связано с формированием умения правильно подбирать слова, математические термины, точно и кратко выражать свои мысли. Конкретно-образное мышление преобладает у дошкольников и младших школьников, у подростковабстрактное. Наглядные компоненты мышления не исчезают с возрастом, а сохраняются и развиваются, продолжая играть важную роль в общей структуре мышления. Приемы на развитие логического мышления: - «Поиск общего» ; - «Исключение лишнего» ;

4. Ожидаемые результаты освоения раздела программы n n n n Теоретически учащиеся должны освоить: - понятие многочлена, стандартного вида многочлена. Умение описывать словами правила выполнения арифметических операций над многочленами; - понятие разложения многочлена на множители. Умение описывать словами суть метода вынесения общего множителя за скобки, метода группировки. Практически учащиеся должны освоить: - приведение многочлена к стандартному виду; - сложение и вычитание многочленов, приведение подобных членов, сложение членов с противоположными коэффициентами; - умножение многочлена на одночлен и на многочлен; - решение уравнений, сводящихся после выполнения арифметических операций над входящими в их состав многочленами, к уравнению вида ах = b; - решение соответствующих текстовых задач; - использование для разложения многочлена на множители метода вынесения общего множителя за скобки, метода группировки; - использование разложения на множители для решения уравнений и доказательства тождеств.

4. Ожидаемые результаты освоения раздела программы - Учащиеся научатся выполнять сложение, вычитание и умножение многочленов, разложение многочлена на множители и применять их в новых ситуациях (преобразования выражений, решения уравнений). - Первоначальную инструкция принимают по-разному (нуждаются в повторном предъявлении инструкции); - Последующую инструкцию дети принимают с первого предъявления, однако, не исключена ситуативная помощь; - В некоторых случаях предполагается стимулирующая помощь (предполагаются наводящие вопросы). Учащиеся отвечают у доски и умеют объяснять свои действия, обоснованно отвечая на вопросы учителя. Умеют найти допущенную ошибку в своем решении, объективно оценить свою работу. Способность к творческому решению учебных и практических задач только на уровне умения применить полученные знания в новой ситуации.

5. ФОРМЫ И МЕТОДЫ ОРГАНИЗАЦИИ ДЕЯТЕЛЬНОСТИ n Традиционный урок комбинированного типа. n Используемые методы организации деятельности учащихся: - Словесный метод; Наглядный ; Устное объяснение; Практический; Уяснение знаний в процессе решения задач; Репродуктивный; Метод уяснения готовых знаний из печатного источника. -

6. СИСТЕМА ЗНАНИЙ И СИСТЕМА ДЕЯТЕЛЬНОСТИ Действия и алгебраические преобразования над многочленами выполняются с использованием известных 1. Свойств арифметических действий над числами. Например, при умножении многочлена на одночлен применяется распределительное свойство умножения с последующими преобразованиями. Это же свойство используется приведении подобных членов. 2. Свойства степеней с натуральным показателем и их применение в преобразовании выражений. 3. Решение уравнений, сводящихся после выполнения арифметических операций над входящими в их состав многочленами, к уравнению вида ах = b.

7. ПОУРОЧНОЕ ПЛАНИРОВАНИЕ ГЛАВА IV. МНОГОЧЛЕНЫ (20 часов) Глава IV Многочлены 20 § 9. Сумма и разность многочленов п. 25. Многочлен и его стандартный вид п. 26. Сложение и вычитание многочленов § 10. Произведение одночлена и многочлена п. 27. Умножение одночлена на многочлен п. 28. Вынесение общего множителя за скобки 4 2 2 6 3 3 Контрольная работа № 5 § 11. Произведение многочленов п. 29. Умножение многочлена на многочлен п. 30. Разложение многочлена на множители способом группировки Контрольная работа № 6 1 8 4 4 1

8. РАЗРАБОТКА УРОКА Тема: Сложение и вычитание многочленов. Класс: 7 «А» . Дата проведения: 17 декабря 2013 года. Тип урока: Комбинированный. Цели урока: научить учащихся складывать и вычитать многочлены. Оборудование: учебник «Алгебра, 7» Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворов – М. : Просвещение, 2012; записи на доске; плакаты; карточки для индивидуальной самостоятельной работы. Тема «Многочлен» играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Главная проблема урока: n преобразование выражений (раскрытие скобок и приведение подобных членов); n вычислительные навыки.

ЭТАПЫ И ВИДЫ ДЕЯТЕЛЬНОСТИ УЧЕНИКОВ 1. Организационный момент 2 мин. 2. Актуализация опорных знаний и умений а) проверка домашнего задания 7 мин. б) устный счет Быстрое включение всех учащихся в деловой ритм Учащиеся сверяют свое решение с решением на слайде, вносят дополнения, исправления, задают вопросы Учащиеся устно отвечают на вопросы учителя Выявление уровня знаний, определение типичных недостатков в знаниях и ликвидация их. Закрепление материала по ходу решения. Основа для продолжения изучения темы Одна из форм тренировки механической памяти учащихся, способствует концентрации внимания.
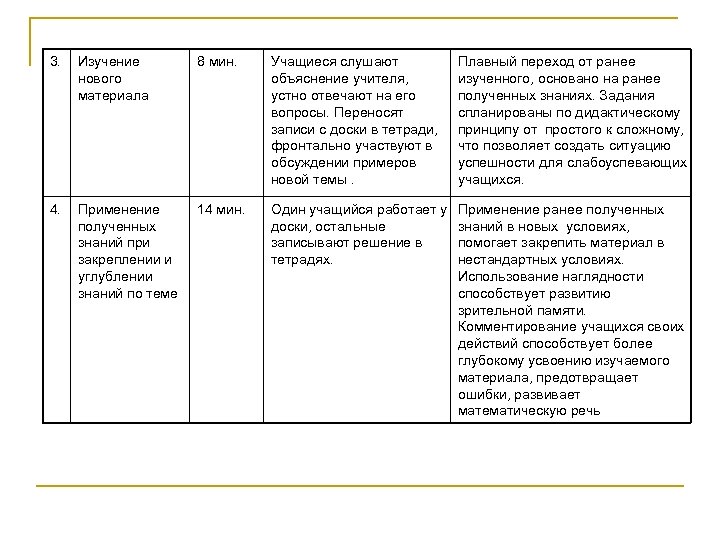
3. Изучение нового материала 8 мин. Учащиеся слушают объяснение учителя, устно отвечают на его вопросы. Переносят записи с доски в тетради, фронтально участвуют в обсуждении примеров новой темы. Плавный переход от ранее изученного, основано на ранее полученных знаниях. Задания спланированы по дидактическому принципу от простого к сложному, что позволяет создать ситуацию успешности для слабоуспевающих учащихся. 4. Применение полученных знаний при закреплении и углублении знаний по теме 14 мин. Один учащийся работает у доски, остальные записывают решение в тетрадях. Применение ранее полученных знаний в новых условиях, помогает закрепить материал в нестандартных условиях. Использование наглядности способствует развитию зрительной памяти. Комментирование учащихся своих действий способствует более глубокому усвоению изучаемого материала, предотвращает ошибки, развивает математическую речь
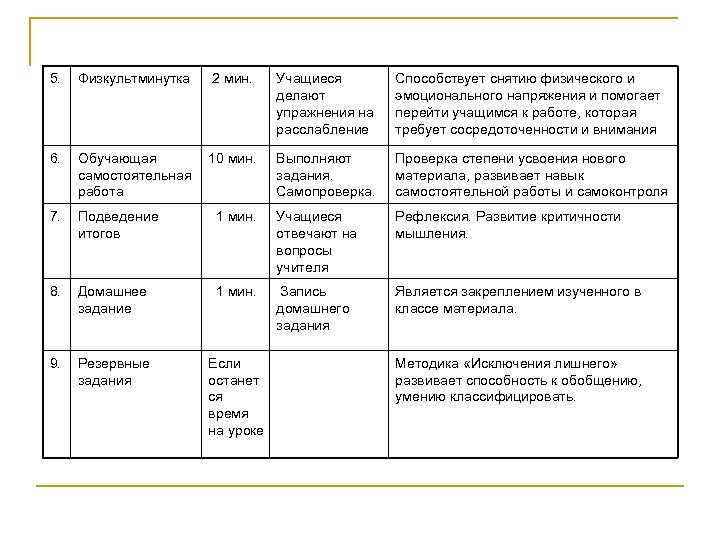
5. Физкультминутка 2 мин. Учащиеся делают упражнения на расслабление Способствует снятию физического и эмоционального напряжения и помогает перейти учащимся к работе, которая требует сосредоточенности и внимания 6. Обучающая самостоятельная работа 10 мин. Выполняют задания. Самопроверка. Проверка степени усвоения нового материала, развивает навык самостоятельной работы и самоконтроля 7. Подведение итогов 1 мин. Учащиеся отвечают на вопросы учителя Рефлексия. Развитие критичности мышления. 8. Домашнее задание 1 мин. Запись домашнего задания Является закреплением изученного в классе материала. 9. Резервные задания Если останет ся время на уроке Методика «Исключения лишнего» развивает способность к обобщению, умению классифицировать.
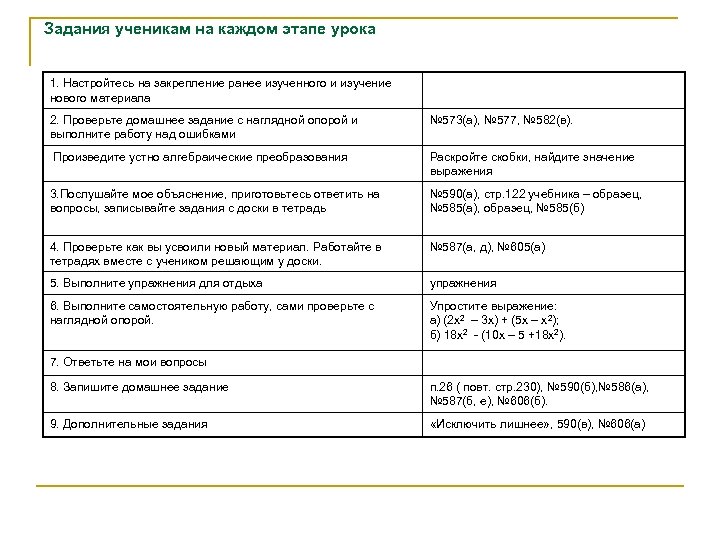
Задания ученикам на каждом этапе урока 1. Настройтесь на закрепление ранее изученного и изучение нового материала 2. Проверьте домашнее задание с наглядной опорой и выполните работу над ошибками № 573(а), № 577, № 582(в). Произведите устно алгебраические преобразования Раскройте скобки, найдите значение выражения 3. Послушайте мое объяснение, приготовьтесь ответить на вопросы, записывайте задания с доски в тетрадь № 590(а), стр. 122 учебника – образец, № 585(а), образец, № 585(б) 4. Проверьте как вы усвоили новый материал. Работайте в тетрадях вместе с учеником решающим у доски. № 587(а, д), № 605(а) 5. Выполните упражнения для отдыха упражнения 6. Выполните самостоятельную работу, сами проверьте с наглядной опорой. Упростите выражение: а) (2 х2 – 3 х) + (5 х – х2); б) 18 х2 - (10 х – 5 +18 х2). 7. Ответьте на мои вопросы 8. Запишите домашнее задание п. 26 ( повт. стр. 230), № 590(б), № 586(а), № 587(б, е), № 606(б). 9. Дополнительные задания «Исключить лишнее» , 590(в), № 606(а)

Предполагаемые результаты выполнения заданий На всех этапах урока учащиеся активно проявляют себя с учетом психологопедагогических особенностей. Под руководством учителя задания выполнят все учащиеся, самостоятельно - несколько человек могут не справится.

Задачи (с решением) № 590(а) а) (а + b) + (a – b) = a + b + a – b = 2 a (a + b) – (a – b) = a + b – a + b = 2 b п. 26 1) (5 х2 + 7 х – 9) + (-3 х2 – 6 х +8) = 5 х2 + 7 х – 9 – 3 х2 – 6 х + 8 = 2 х2 + х – 1 № 585(а) а) (4 х3 – 5 х – 7) + (х3 – 8 х) = 4 х3 – 5 х – 7 + х3 – 8 х = 5 х3 – 13 х – 7 п. 26 2) (х3 + 5 х2 – х + 8) – (х3 – 7 х – 1) = х3 + 5 х2 – х + 8 – х3 + 7 х + 1 = 5 х2 + 6 х + 9 № 585(б) б) (5 у2 – 9) – (7 у2 – у + 5) = 5 у2 – 9 – 7 у2 + у – 5 = -2 у2 + у – 14. № 587(а, д) а) (1 + 3 а) + (а 2 – 2 а) = 1 + 3 а + а 2 – 2 а = а 2 + а + 1 д) (8 n 3 – 3 n 2) – (7 + 8 n 3 – 2 n 2) = 8 n 3 – 3 n 2 – 7 – 8 n 3 + 2 n 2 = - n 2 – 7 № 605(а) Решите уравнение: а) (23 +3 х) + (8 х – 41) = 15 23 + 3 х + 8 х – 41 = 15 11 х – 18 = 15 11 х = 15 + 18 11 х = 33 : 11 х=3 Ответ: х = 3.

№ 590(в) в) (-a –b) + (a – b) = -a –b + a –b = -2 b (-a –b) - (a – b) = -a –b –a + b = -2 a № 587(в) в) (у2 – 5 у) + (5 у – 2 у2) = у2 – 5 у + 5 у – 2 у2 = -у2 № 606(а) Решите уравнение: 8 у – 3 – (5 – 2 у) = 4, 3 8 у – 3 – 5 + 2 у = 4, 3 10 у – 8 = 4, 3 10 у = 4, 3 + 8 10 у = 12, 3 : 10 у = 1, 23 Ответ: у = 1, 23

Слайд № 1. Проверка домашнего задания № 573(а). Найдите значение многочлена: а) 6 а 3 - а 10 + 4 а 3 + а 10 – 8 а 3 + а = 2 а 3 + а При а = -3 2 (-3)3 + (-3) =2 (-27) -3 = -54 -3 = -57 № 577. Расположите члены многочлена по убывающим степеням переменной: а) 17 а 4 – 8 а 5 + 3 а – а 3 – 1 = -8 а 5 +17 а 4 – а 3 + 3 а – 1; б) 35 – с6 + 5 с2 – с4 = -с6 – с4 + 5 с2 + 35. № 582(в). Решите уравнение: в)

Слайд № 2. Устный счет плюс – переписываем минус - меняем 3) Раскрыть скобки: а) 3 х + (2 – у); в) 5 + (12 – 2 b); б) (а + b) – (с – d); г) 64 – (14 + 7 х). 4) Найдите значение выражения: а) -5, 7 + (19 б)-4 + 5, 7); - (8 – 4 ); в) 12, 3 + 4 х – (4 х + 12, 3). Задание: исключить лишнее 3 х2; -4 х; 3 х + 8 у 2 – 7; 4 у; 18 х 2.

Слайд № 3. Самостоятельная работа Алгоритм сложения и вычитания многочленов 1. Раскрыть скобки 2. Привести подобные члены Упростите выражение: а) (2 х2 – 3 х) + (5 х – х2) б) 18 х2 – (10 х – 5 +18 х2)

Слайд № 4. Решение самостоятельной работы а) (2 х2 – 3 х) + (5 х – х2) = 2 х2 – 3 х + 5 х – х2 = х 2 + 2 х а) Ответ: х2 + 2 х б) 18 х2 – (10 х – 5 +18 х2) = 18 х2 – 10 х + 5 – 18 х2 = -10 х +5 б) Ответ: -10 х + 5

Задание ученикам по рефлексии их деятельности Чем занимались на уроке? Есть ли у кого ко мне вопросы? Что было непонятно? Формы контроля и оценки результатов урока Устный счет; Самостоятельная работа обучающего характера; Самоконтроль. Задания на дом п. 26 (повторить стр. 230) № 590(б); № 586(а); № 587(б, е); № 606(б). На следующем уроке проверочная домашняя работа. Рекомендуемые ученикам материалы учебник «Алгебра, 7» Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворов – М. : Просвещение, 2012;

Карточка № 1. Раскрытие скобок ПРАВИЛА ОБРАЗЦЫ ЗАДАНИЯ Если перед скобкой стоит плюс или не стоит никакой знак, то можно убрать скобки, сохраняя знаки всех слагаемых, стоящих внутри скобок. (а - b + с) = а - b + с, + (x + y - z) = x + y -z, + (- а + с-1) = - а + с-1. Раскрыть скобки: Если перед скобкой стоит минус, то можно убрать скобки, меняя знаки всех слагаемых, стоящих внутри скобок. -(а - х + с) = - а + х -с, -(1 -х + а) = -1 + х -а. 1) (x + y-z)-1; 2) х + (у -х); 3) х - (x - y +z); 4) (х + у)-(х -у); 5) (х - у + z) - (х + у - z). 6) (a + b - c) + 2; 7) a + (b -c); 8) a - (a - b + c); 9) (x + y) - (x - y); 10) (a - b + 1) - (a + b - 1). 11) (m + p - q) - p; 12) m + (p - m); 13) m - (m - p + q); 14) (p + q) - (p - q); 15) (m - p + 5) - (m + p - 3).

Карточка № 2. Умножение многочленов ПРАВИЛА ОБРАЗЦЫ Чтобы умножить многочлен на (а + b - с)(х - у) = многочлен, умножь каждый член = ах – ау + bх - by – с х + су. первого многочлена на каждый член второго многочлена и сложи результаты. ЗАДАНИЯ Преобразовать произведение в многочлен: 1) (а + b)(c + d) ; 2) (а + 2)(b - с) ; 3) (а - 1)(а + b - 2); 4) (a - b) (a + b); 5) (a + b). 6) (x + y) (z + t); 7) (x + 2)(y - z); 8) (х - 1)(х + у - 3); 9) (х - у)(х + у); 10) (х + 1). 11) (m + n) (p + q); 12) (т + 2) (n - р); 13) (m - 1)(m + n - 2); 14) (т - р)(т + р) ; 15) (m + 2).

Карточка № 3. Разложение многочлена на множители вынесением за скобки ПРАВИЛА ОБРАЗЦЫ ЗАДАНИЯ Если у всех членов многочлена есть общий множитель, его можно вынести за скобки; в скобках нужно записать частные от деления каждого члена на этот множитель. ах + ау - а = а (х + у - 1). Разложить на множители: 1) 2 х -2 у ; 2) 3 x y+ 4 x z ; 3) 3 х2 – 2 х; 4) 6 ху – 3 x z + 9 х2 ; 5) (х-1)а + 2(х-1)с. 6) 3 а-3 b; 7) 2 ас + 5 bс; 8) 7 а 2 - За; 9) 6 ad + 2 cd-4 d 2; 10) (а + 2)х + 3(а + 2)у. 11) 4 p-4 q; 12) p q + 2 mp; 13) q 2 -7 q; 14) 6 ay - 3 az + 9 a 2; 15) (m + 1)a + 4(m + 1)b.

Контрольная работа № 5 (п. 25 – 28) § 1. Выполните действия: а)( 3 а – 4 ах + 2) – (11 а – 14 ах); § 2. Вынесите общий множитель за скобки: а) 10 аb – 15 b 2; § § б) 3 у 2 (у3 + 1). б) 18 а 3 + 6 а 2 3. Решите уравнение 9 х – 6(х – 1) = 5(х + 2). 4. Пассажирский поезд за 4 ч прошел такое же расстояние, какое товарный за 6 ч. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше. 5. Решите уравнение 6. Упростите выражение 2 а(а +b – с) – 2 b(а – b – с) + 2 с(а – b + с).

Контрольная работа № 6 (п. 29 – 30) n 1. Выполните умножение: а) (с +2)(с – 3); в) (5 х – 2 у)(4 х – у); б) (2 а – 1)(3 а + 4); г) (а – 2)(а 2 - 3 а +6). § 2. Разложите на множители: а) а(а +3) – 2(а + 3); б) ах – ау + 5 х – 5 у. 3. Упростите выражение -0, 1 х(2 х2 +6)(5 – 4 х2). 4. Представьте многочлен в виде произведения: а) х2 – ху – 4 х + 4 у; б) аb – ac – bx + cx +c – b. 5. Из прямоугольного листа фанеры вырезали квадратную пластинку, для чего с одной стороны листа фанеры отрезали полосу шириной 2 см, а с другой 3 см. Найдите сторону получившегося квадрата, если известно, что его площадь на 51 см 2 меньше площади прямоугольника.

Тест «Многочлены» n 1. Найдите степень многочлена: 4, 5 х6 + 3 ху3– 2, 5 х2 – 6 ху6 + у2. а) 8; б) 6; n в) 7; г) другой ответ. 2. Упростите выражение: (2 а + 3 b) + (7 b – 3 a) – (8 a – 6 b). а) 13 а + 16 b; б) -9 а + 16 b; n в) 7 а + 16 b; г) другой ответ. 3. Выполните умножение: 0, 5 у( -2 у2 – 6 у + 12). а) у3 + 3 у2 + 6; б) – у3 + 3 у2 + 6; n в) –у2 – 3 у + 6; г) другой ответ. 4. Разложите на множители: 15 b 2 + 25 b – 30 ab. а) 15 b( b + 10 – 15 a); б) 5 b( b + 5 – a); n в) 5 b(b + 5 – 6 a); г) другой ответ. 5. Упростите выражение: 7(у – а)(а + у) + 7 а 2. а) 7 у2 + 14 уа + 14 а 2; б) 7 у2; n в) 7 у2 – 14 а 2; г) другой ответ. 6. Решите уравнение: 4 х2 + 24 х = 0. а) 6; в) 3; в) -6; г) другой ответ.

Ответы: К. р. № 5 № 1. а) -8 а + 10 ах + 2; б) 3 у5 + 3 у2. № 2. а) 5 b(2 а – 3 b); № 3. -2. № 4. 60 км/ч. б)6 а 2 (3 а + 1). № 5. 2, 6. № 6. 2 а 2 + 2 b 2 + 2 c 2. К. р. № 6. № 1. а) с2 – с – 6; б) 6 а 2 + 5 а – 4; в) 20 х2 – 13 ху + 2 у2; г) а 3 – 5 а 2 + 12 а – 12. № 2. а) а 2 + а – 6; б) (х – у)(а + 5). № 3. 0, 8 х5 + 1, 4 х3 – 3 х. № 1. 2. Тест «Многочлены» в б № 4 а) (х – у)(х – 4); б) (b – с) (а – х – 1). 3. 4. 5. 6. г г б г № 5. 9 см.

9. СПИСОК ЛИТЕРАТУРЫ 1. Алгебра: учеб. для 7 кл. общеобразоват. учреждений /[Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 18 -е изд. - М. : Просвещение, 2012. 2. Ерина Т. М. Поурочное планирование по алгебре. 7 класс: к учебнику Ю. Н. Макарычева и др. «Алгебра: 7 класс» / Т. М. Ерина. – 2 -изд. , перераб. и доп. – М. : Издательство «Экзамен» , 2008. 3. Жохов В. И. , Крайнева Л. Б. Уроки алгебры в 7 классе: Пособие для учителей к учебнику «Алгебра, 7» Ю. М. Макарычева и др. – М. : Вербум-М, 2000. 4. Гилярова М. Г. Алгебра. 7 класс. /Поурочные планы по учебнику «Алгебра. 7 класс» (Макарычев Ю. Н. и др. ) /Сост. М. Г. Гилярова. – Волгоград: Учитель – АСТ, 2003. 5. Программы образовательных учреждений. Алгебра 7 -9 классы. Составитель Бурмистрова Т. А. – М. : Просвещение, 2009. авт. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова 6. Звавич Л. И. и др. Дидактические материалы по алгебре для 7 класса – М. : Просвещение, 1995 7. Математические диктанты для 5 -9 классов: Кн. для учителя/ Е. Б. Арутюнян, М. Б. Волович, Ю. А. Глазков, Г. Г. Левитас. – М. : Просвещение, 1991. 8. Г. Г. Левитас. Карточки для коррекции знаний учащихся по алгебре для 7 класса. – М. : Илекса, 1999. 9. Тесты. Математика. 5 -11 кл. – М. : ООО «Агентство «КРПА «Олимп» : ООО «Издательство АСТ» , 2002. 10. А. П. Ершова, В. В. Голобородько, А. С. Ершова. Самостоятельные и контрольные работы по алгебре для 7 класса. Разноуровневые дидактические материалы. – М. : Илекса, Харьков: Гимназия, 2003.
7d56ebe935b9689c420c52356b9711b7.ppt