d6fabb8f2e70fa02510a462a13b10174.ppt
- Количество слайдов: 136

Algebra 2 Interactive Chalkboard Copyright © by The Mc. Graw-Hill Companies, Inc. Send all inquiries to: GLENCOE DIVISION Glencoe/Mc. Graw-Hill 8787 Orion Place Columbus, Ohio 43240

Lesson 9 -1 Multiplying and Dividing Rational Expressions Lesson 9 -2 Adding and Subtracting Rational Expressions Lesson 9 -3 Graphing Rational Functions Lesson 9 -4 Direct, Joint, and Inverse Variation Lesson 9 -5 Classes of Functions Lesson 9 -6 Solving Rational Equations and Inequalities

Example 1 Simplify a Rational Expression Example 2 Use the Process of Elimination Example 3 Simplify by Factoring Out – 1 Example 4 Multiply Rational Expressions Example 5 Divide Rational Expressions Example 6 Polynomials in the Numerator and Denominator Example 7 Simplify a Complex Fraction
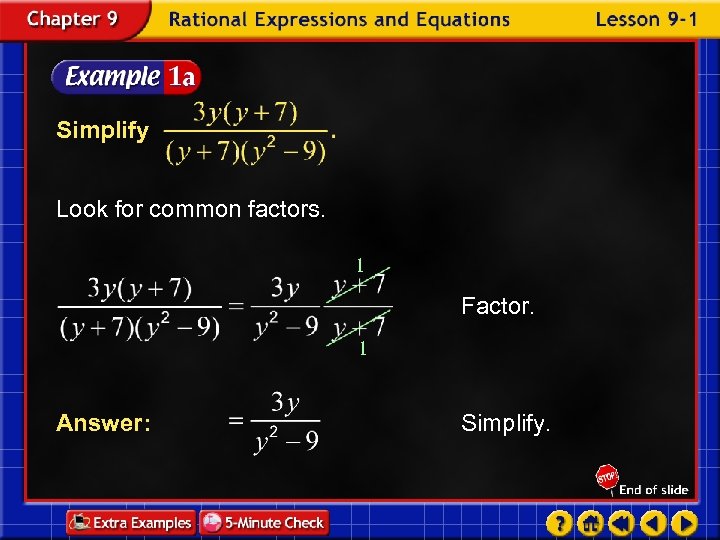
Simplify Look for common factors. 1 Factor. 1 Answer: Simplify.

Under what conditions is this expression undefined? A rational expression is undefined if the denominator equals zero. To find out when this expression is undefined, completely factor the denominator. Answer: The values that would make the denominator equal to 0 are – 7, 3, and – 3. So the expression is undefined at y = – 7, y = 3, and y = – 3. These values are called excluded values.
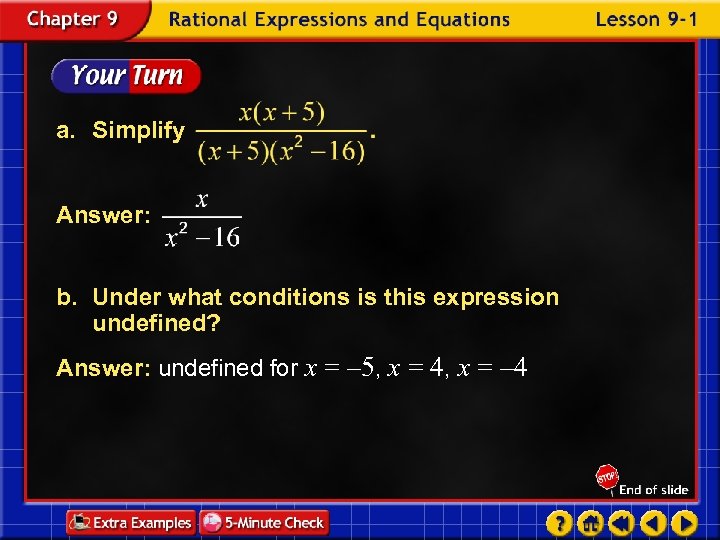
a. Simplify Answer: b. Under what conditions is this expression undefined? Answer: undefined for x = – 5, x = 4, x = – 4
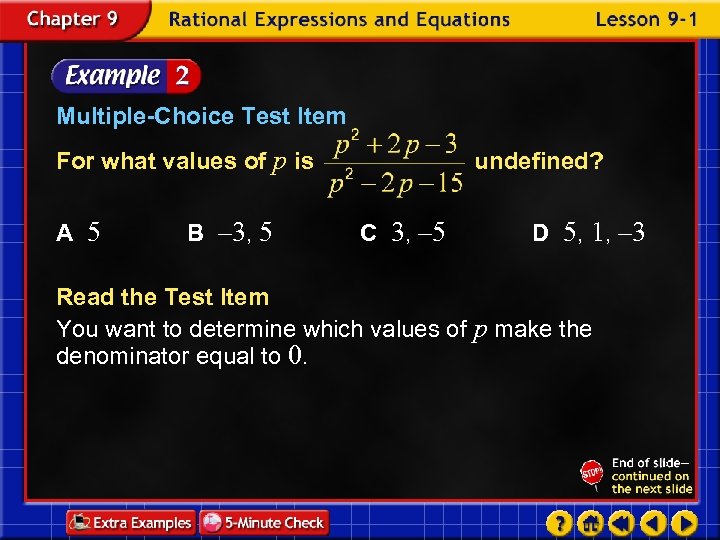
Multiple-Choice Test Item For what values of p is A 5 B – 3, 5 undefined? C 3, – 5 D 5, 1, – 3 Read the Test Item You want to determine which values of p make the denominator equal to 0.
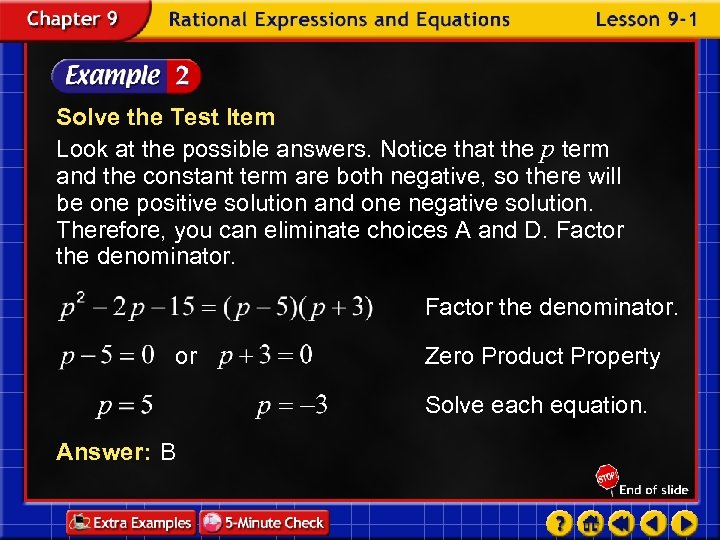
Solve the Test Item Look at the possible answers. Notice that the p term and the constant term are both negative, so there will be one positive solution and one negative solution. Therefore, you can eliminate choices A and D. Factor the denominator. or Zero Product Property Solve each equation. Answer: B
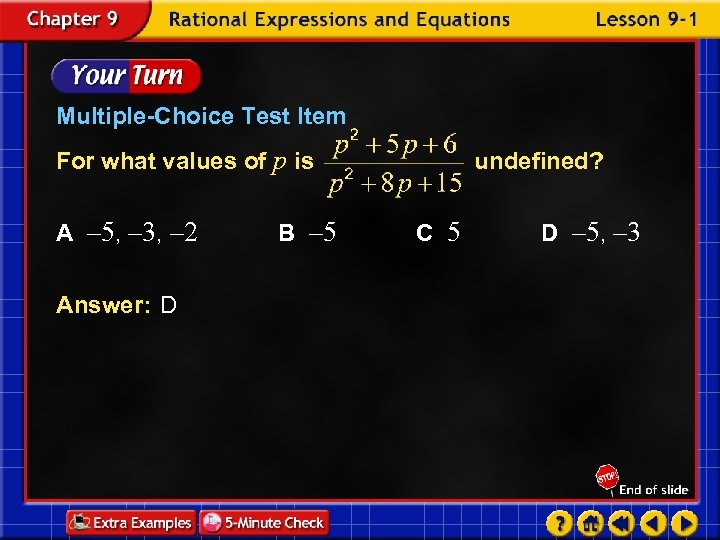
Multiple-Choice Test Item For what values of p is A – 5, – 3, – 2 Answer: D B – 5 undefined? C 5 D – 5, – 3

Simplify Factor the numerator and the denominator. 1 a or 1 Answer: 1 or –a Simplify.
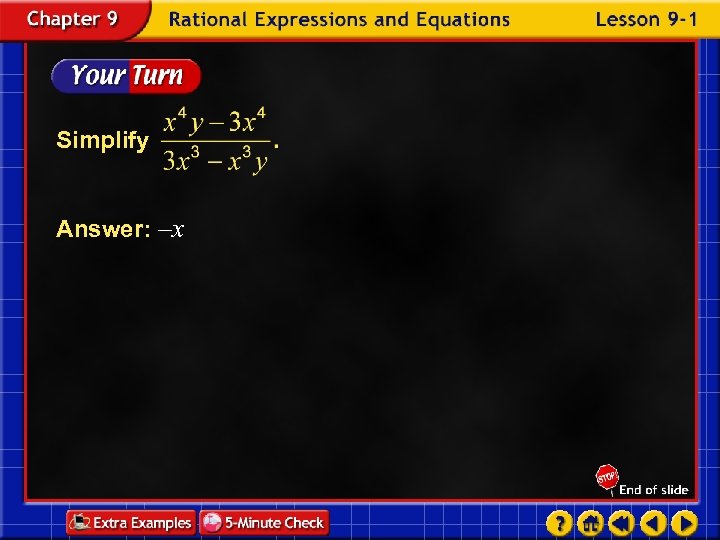
Simplify Answer: –x
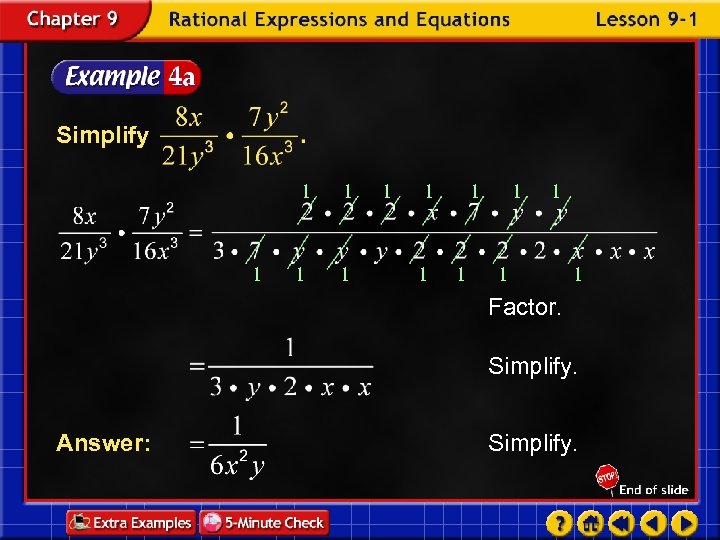
Simplify 1 1 1 1 Factor. Simplify. Answer: Simplify.
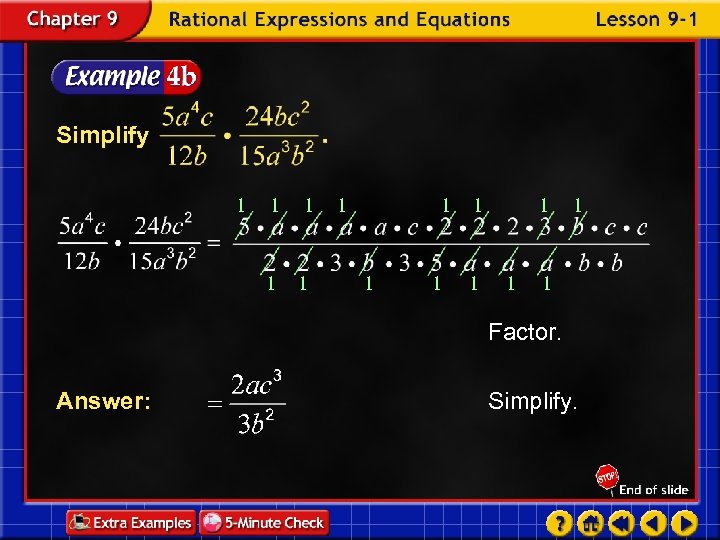
Simplify 1 1 1 1 Factor. Answer: Simplify.

Simplify each expression. a. Answer: b. Answer:

Simplify Multiply by the reciprocal of divisor. 1 1 1 Factor. Simplify. Answer: Simplify. 1 1
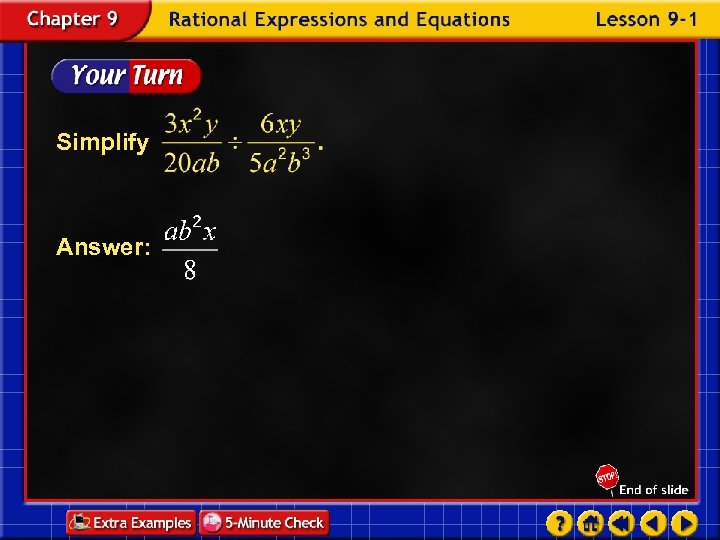
Simplify Answer:
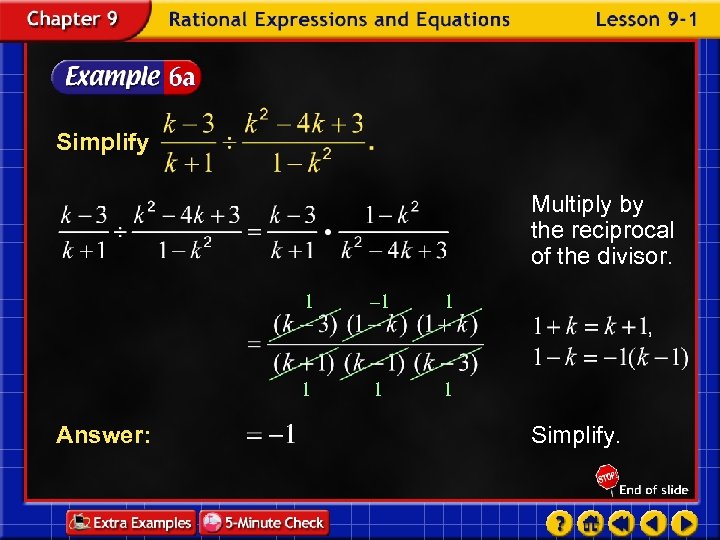
Simplify Multiply by the reciprocal of the divisor. 1 1 1 Answer: – 1 1 1 Simplify.
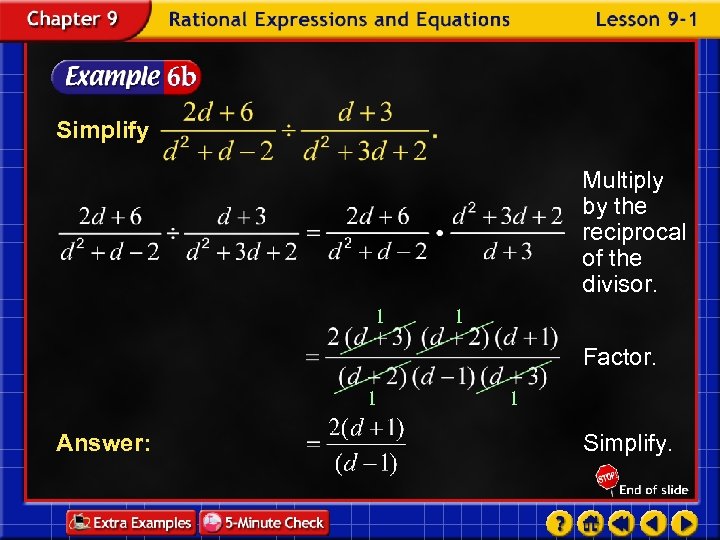
Simplify Multiply by the reciprocal of the divisor. 1 1 Factor. 1 Answer: 1 Simplify.
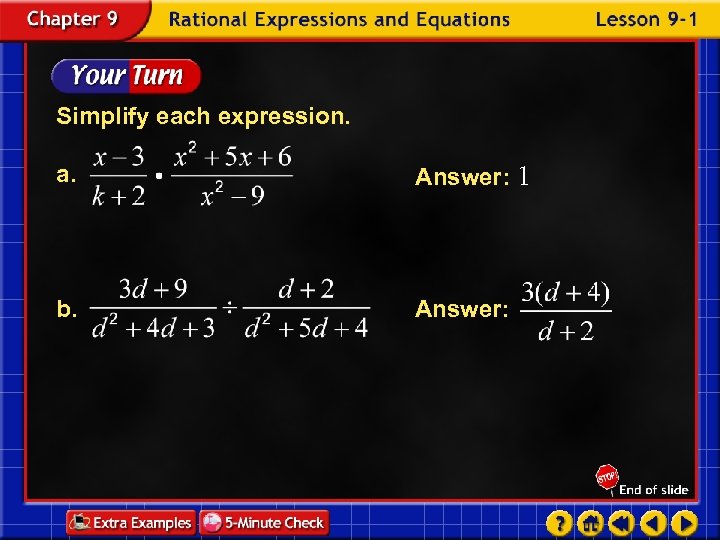
Simplify each expression. a. Answer: 1 b. Answer:
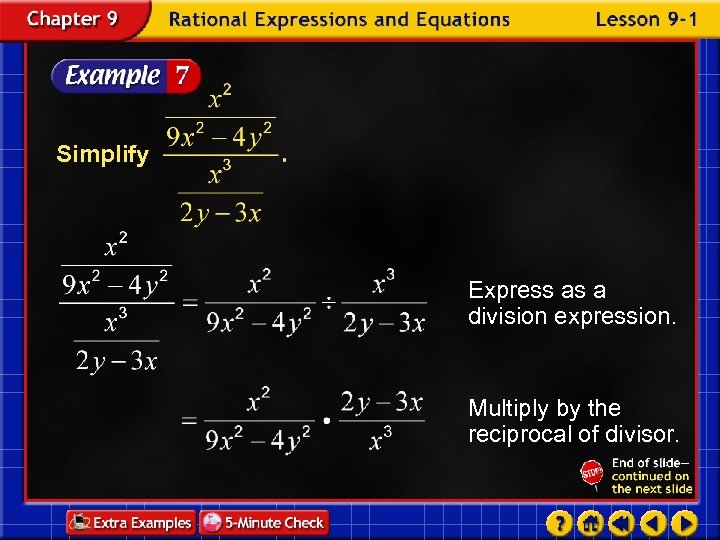
Simplify Express as a division expression. Multiply by the reciprocal of divisor.
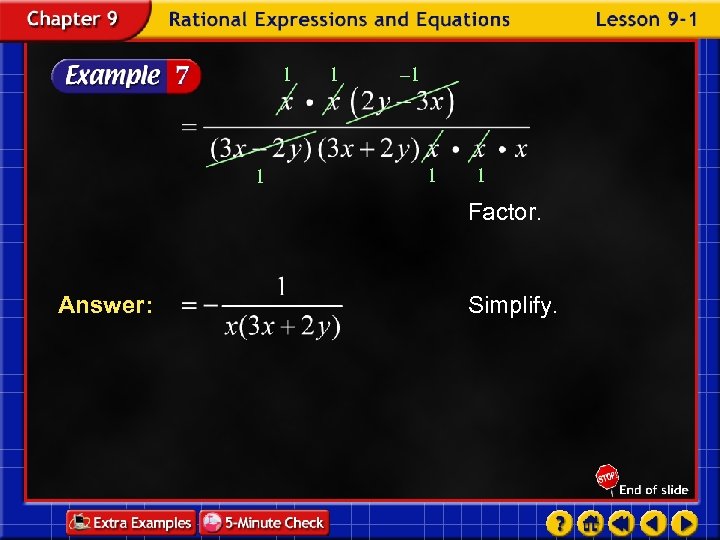
1 1 1 – 1 1 1 Factor. Answer: Simplify.
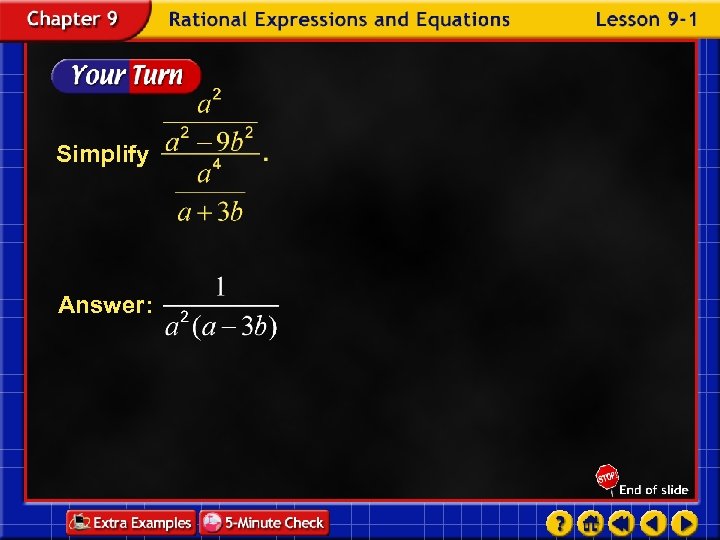
Simplify Answer:

Example 1 LCM of Monomials Example 2 LCM of Polynomials Example 3 Monomial Denominators Example 4 Polynomial Denominators Example 5 Simplify Complex Fractions Example 6 Use a Complex Fraction to Solve a Problem

Find the LCM of 15 a 2 bc 3, 16 b 5 c 2, and 20 a 3 c 6. Factor the first monomial. Factor the second monomial. Factor the third monomial.
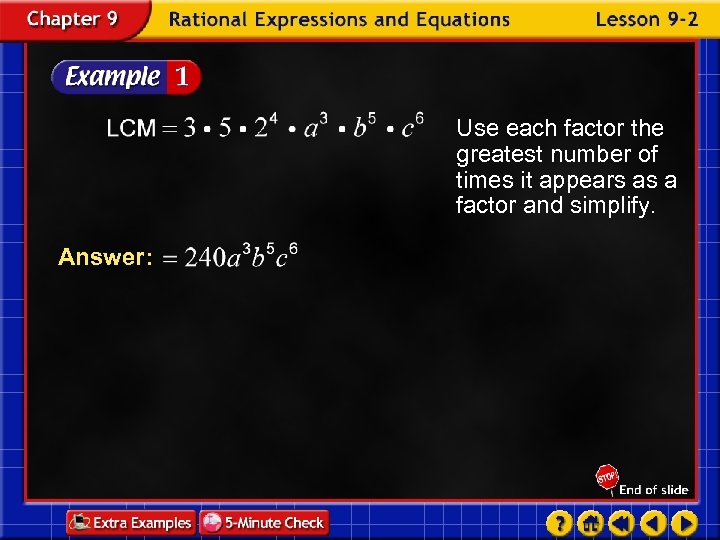
Use each factor the greatest number of times it appears as a factor and simplify. Answer:
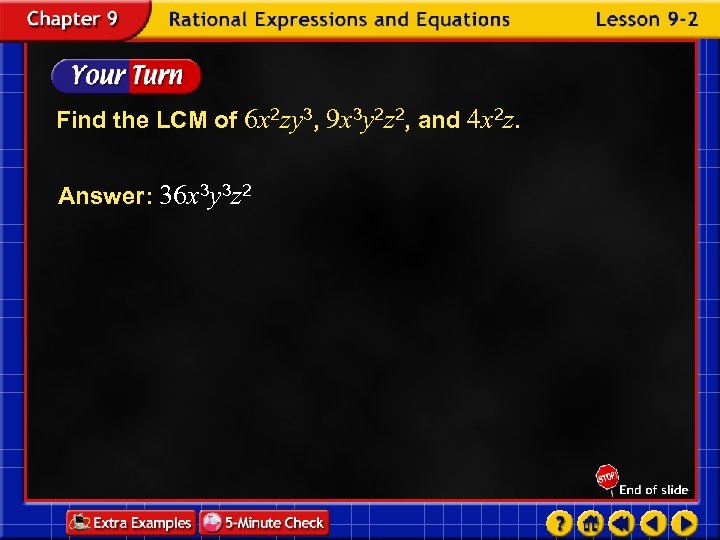
Find the LCM of 6 x 2 zy 3, 9 x 3 y 2 z 2, and 4 x 2 z. Answer: 36 x 3 y 3 z 2
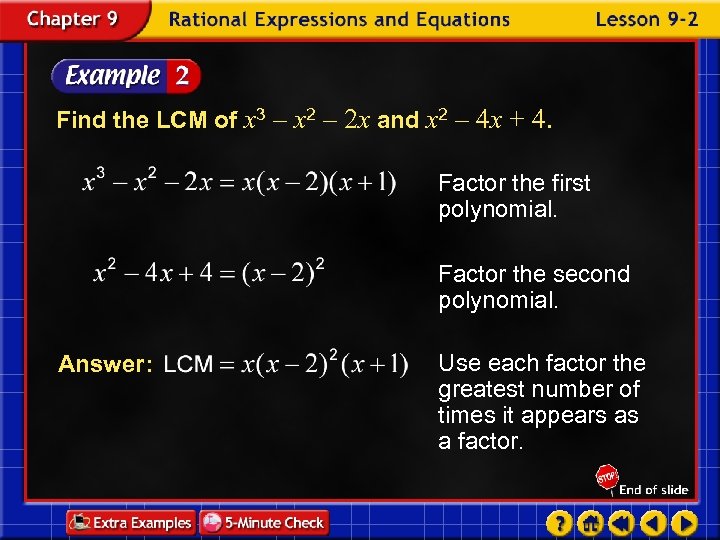
Find the LCM of x 3 – x 2 – 2 x and x 2 – 4 x + 4. Factor the first polynomial. Factor the second polynomial. Answer: Use each factor the greatest number of times it appears as a factor.
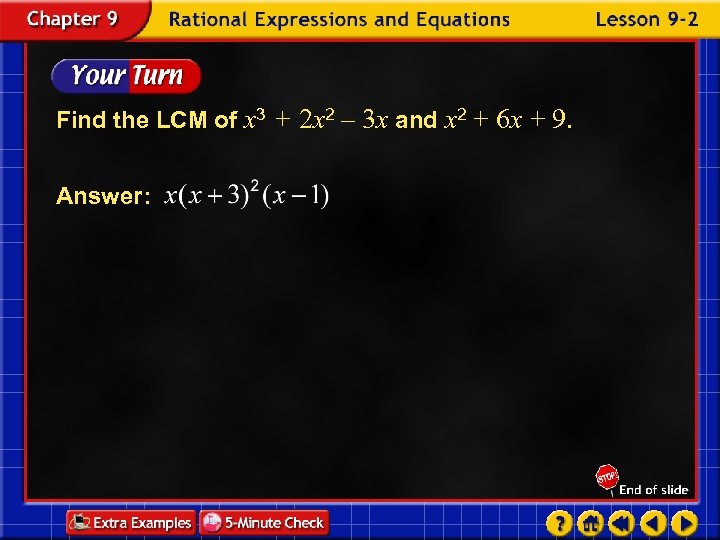
Find the LCM of x 3 + 2 x 2 – 3 x and x 2 + 6 x + 9. Answer:
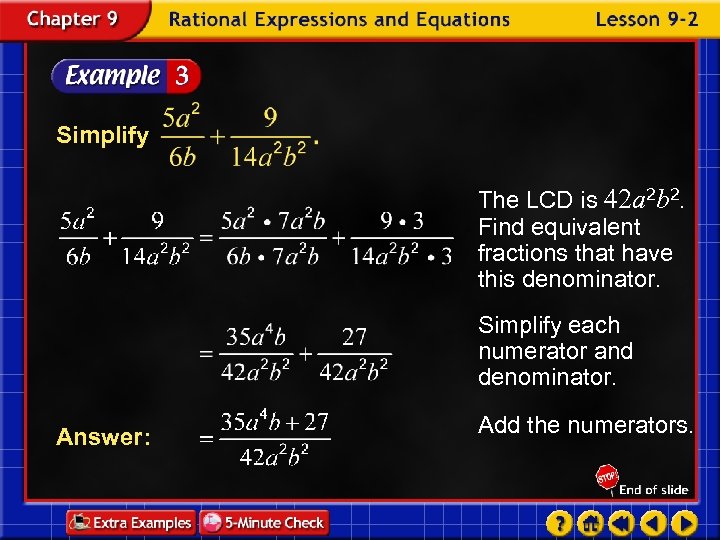
Simplify The LCD is 42 a 2 b 2. Find equivalent fractions that have this denominator. Simplify each numerator and denominator. Answer: Add the numerators.

Simplify Answer:

Simplify Factor the denominators. The LCD is 6(x – 5). Subtract the numerators.
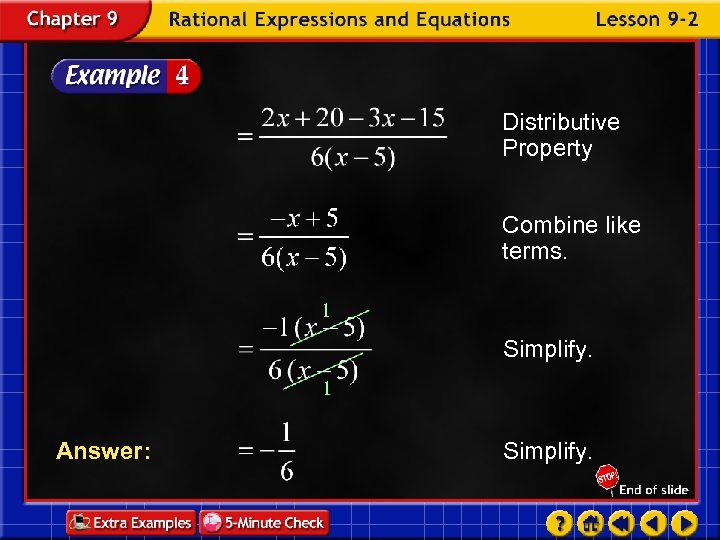
Distributive Property Combine like terms. 1 Simplify. 1 Answer: Simplify.
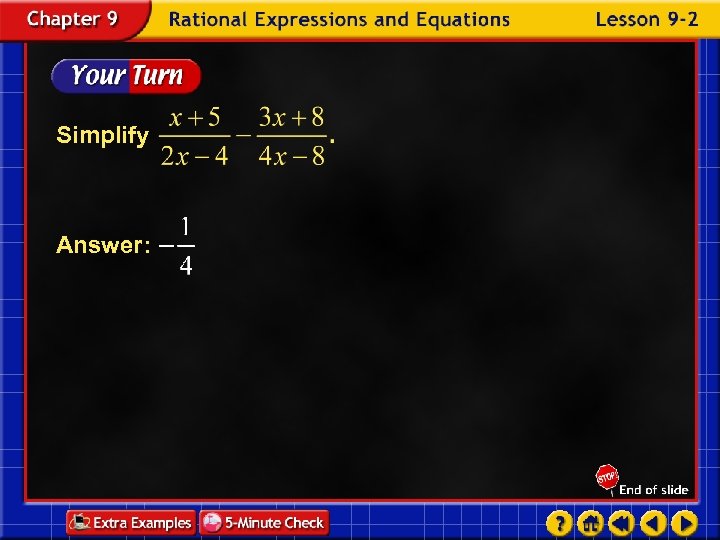
Simplify Answer:
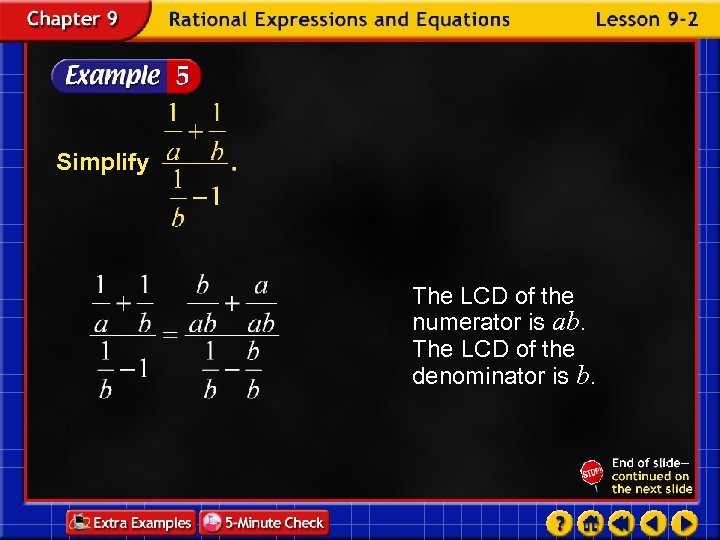
Simplify The LCD of the numerator is ab. The LCD of the denominator is b.

Simplify the numerator and denominator. Write as a division expression. 1 Multiply by the reciprocal of the divisor. 1
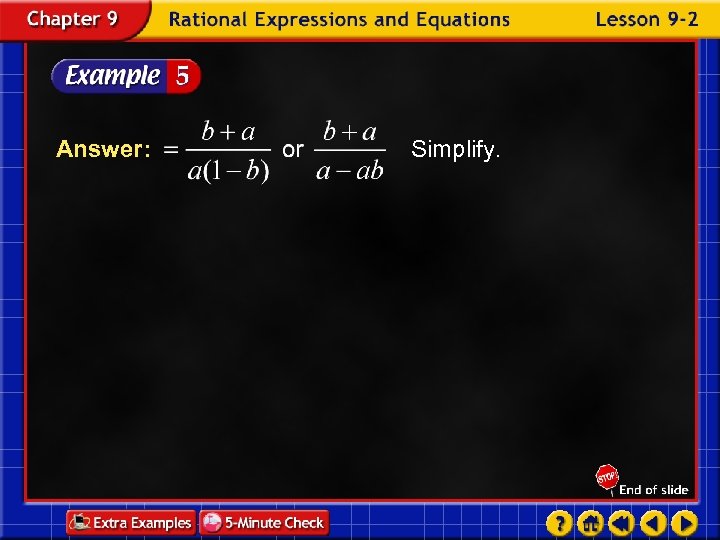
Answer: Simplify.
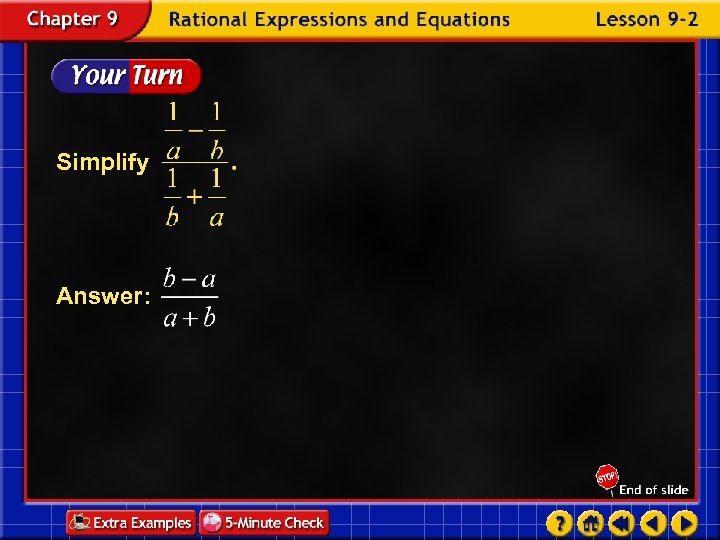
Simplify Answer:
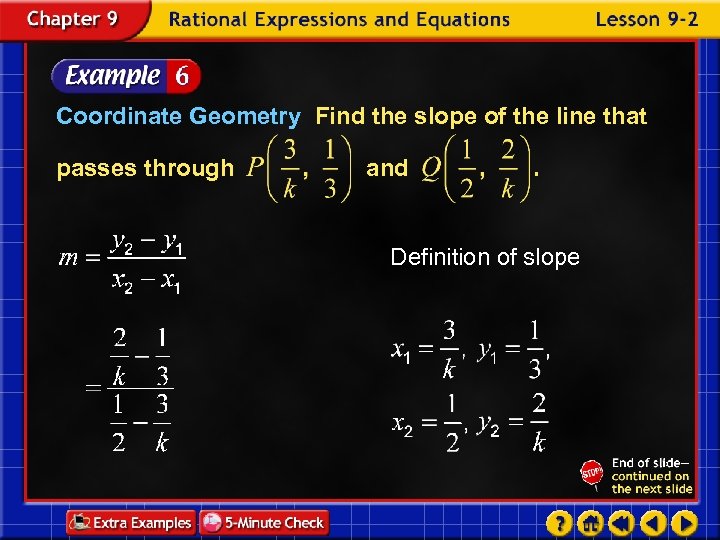
Coordinate Geometry Find the slope of the line that passes through and Definition of slope
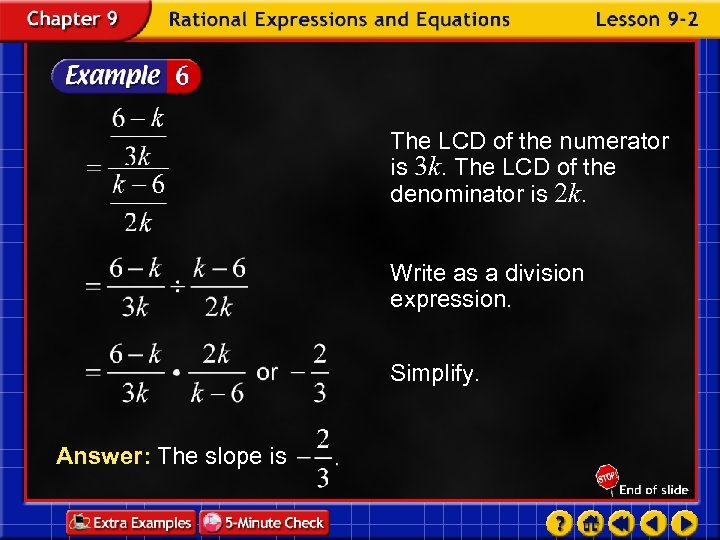
The LCD of the numerator is 3 k. The LCD of the denominator is 2 k. Write as a division expression. Simplify. Answer: The slope is
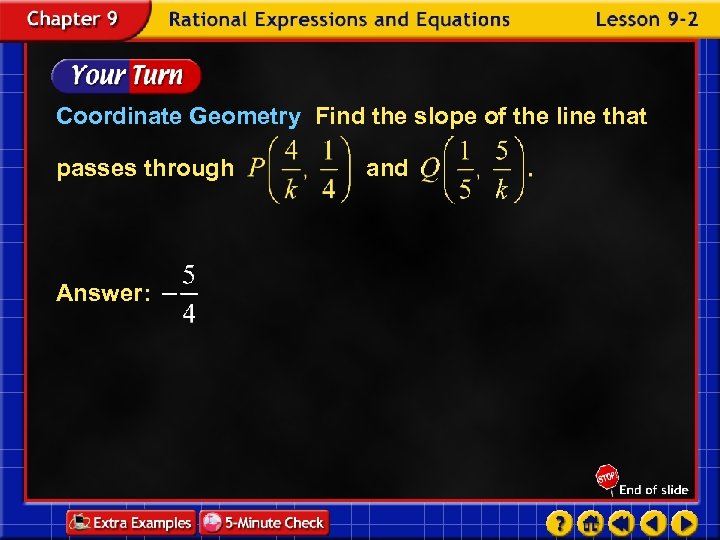
Coordinate Geometry Find the slope of the line that passes through Answer: and

Example 1 Vertical Asymptotes and Point Discontinuity Example 2 Graph with a Vertical Asymptote Example 3 Graph with Point Discontinuity Example 4 Use Graphs of Rational Functions

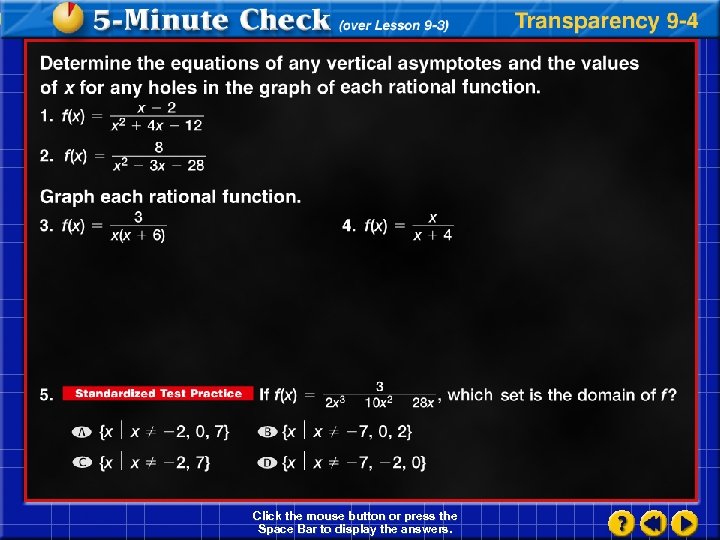
Determine the equations of any vertical asymptotes and the values of x for any holes in the graph of First factor the numerator and denominator of the rational expression.
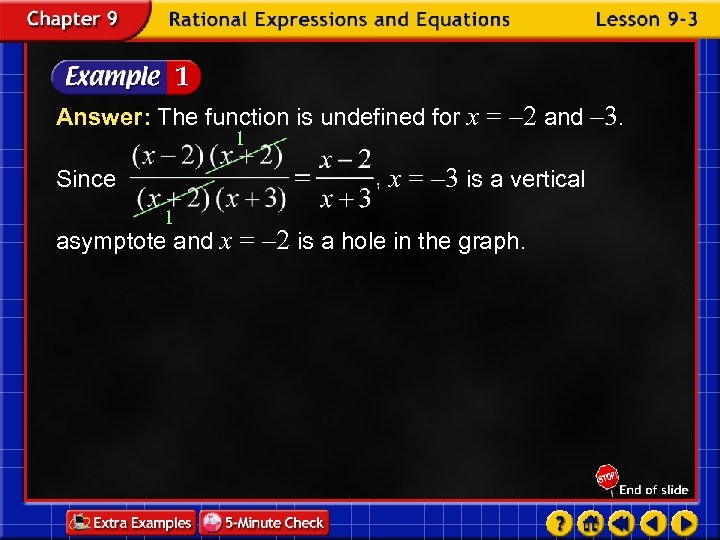
Answer: The function is undefined for x = – 2 and – 3. 1 x = – 3 is a vertical Since 1 asymptote and x = – 2 is a hole in the graph.
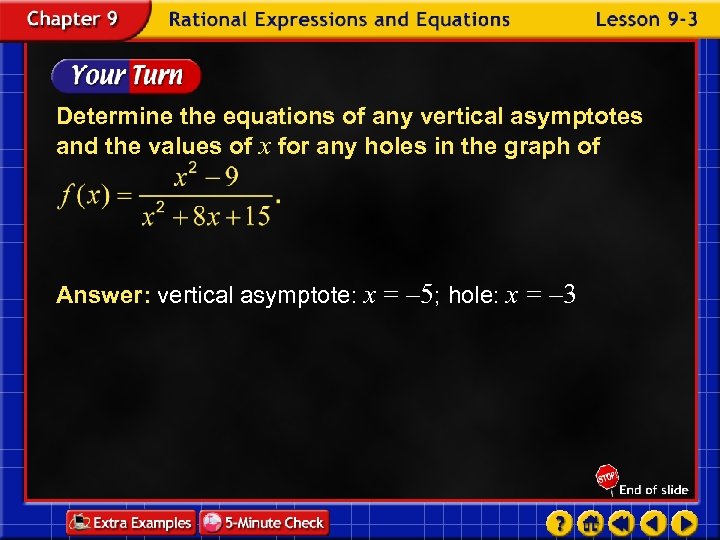
Determine the equations of any vertical asymptotes and the values of x for any holes in the graph of Answer: vertical asymptote: x = – 5; hole: x = – 3
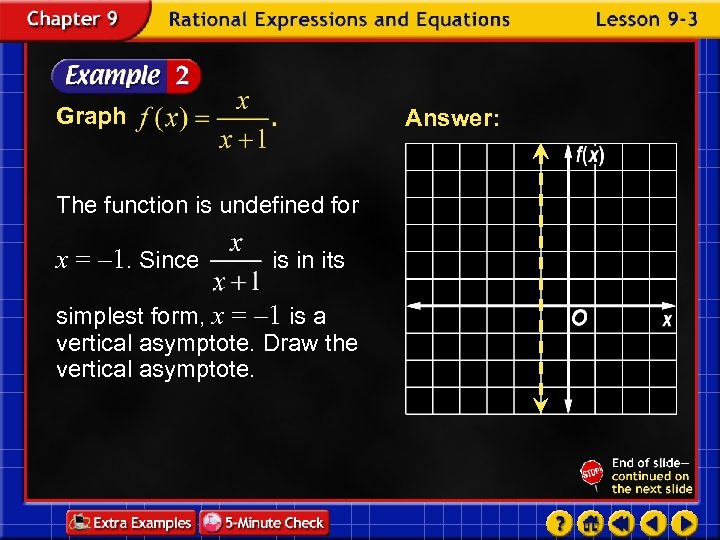
Graph Answer: The function is undefined for x = – 1. Since is in its simplest form, x = – 1 is a vertical asymptote. Draw the vertical asymptote.
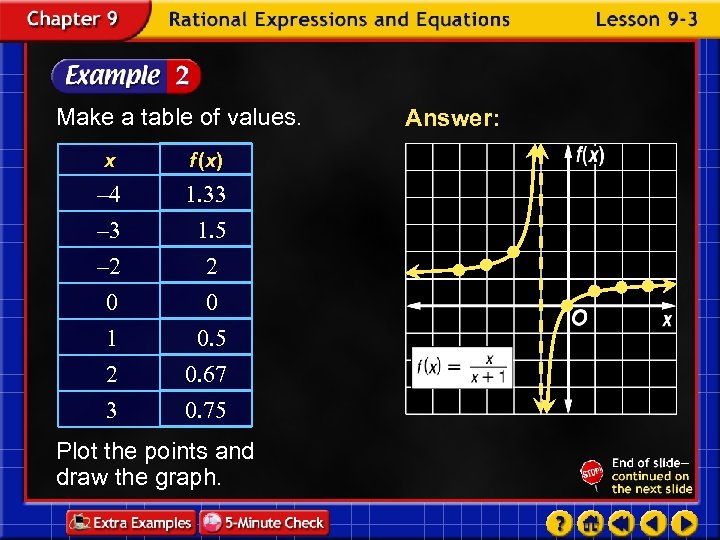
Make a table of values. x f (x) – 4 1. 33 – 2 0 1 1. 5 2 0 0. 5 2 3 0. 67 0. 75 Plot the points and draw the graph. Answer:
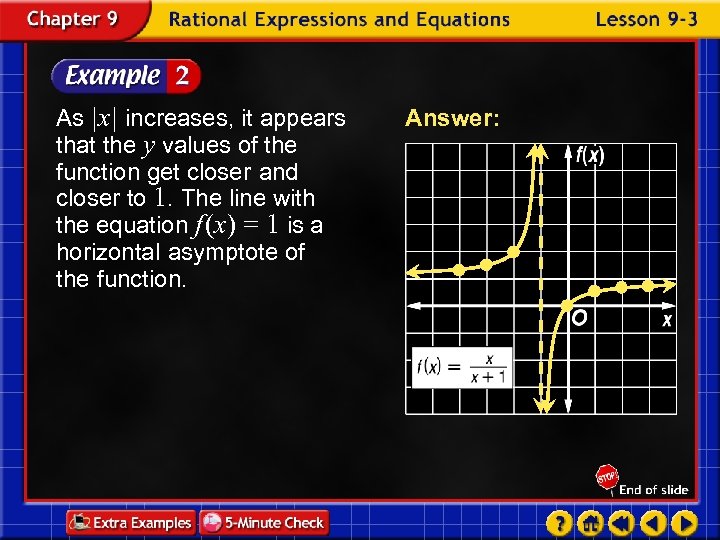
As |x| increases, it appears that the y values of the function get closer and closer to 1. The line with the equation f (x) = 1 is a horizontal asymptote of the function. Answer:
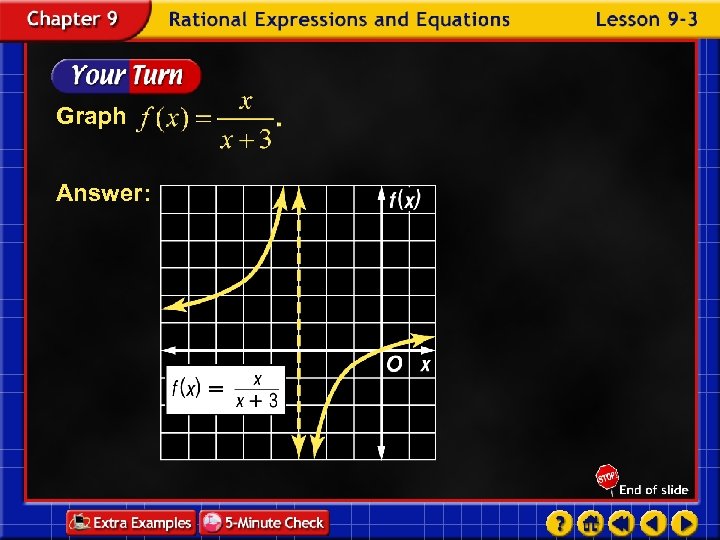
Graph Answer:
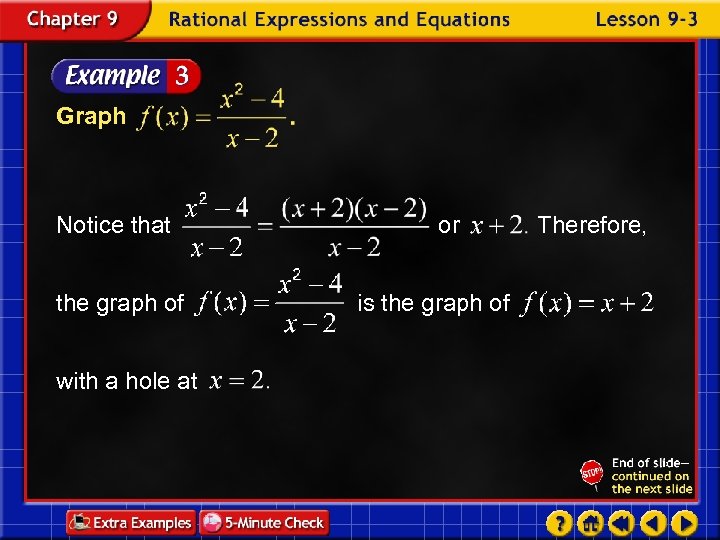
Graph Notice that the graph of with a hole at or is the graph of Therefore,
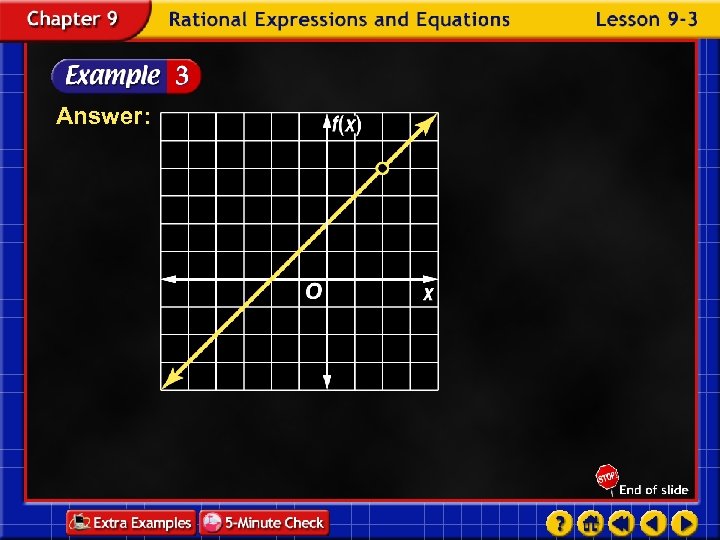
Answer:
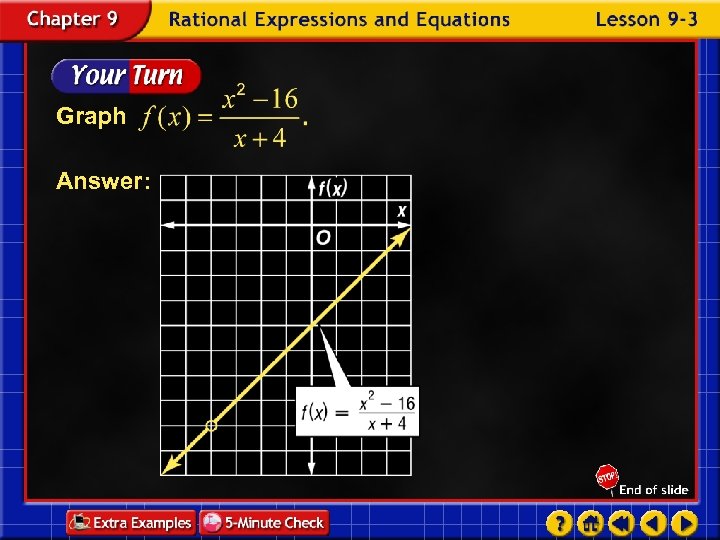
Graph Answer:

Transportation A train travels at one velocity V 1 for a given amount of time t 1 and then another velocity V 2 for a different amount of time t 2. The average velocity is given by Let t 1 be the independent variable and let V be the dependent variable. Draw the graph if V 1 = 50 miles per hour, V 2 = 30 miles per hour, and t 2 = 1 hour.
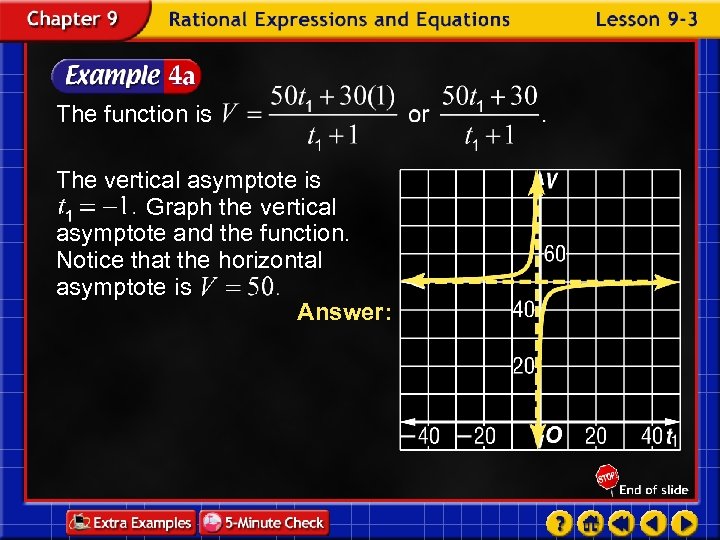
The function is The vertical asymptote is Graph the vertical asymptote and the function. Notice that the horizontal asymptote is Answer:
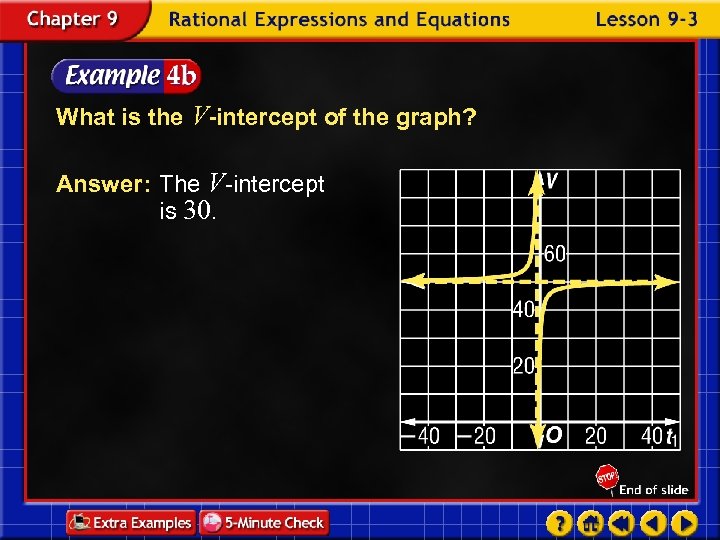
What is the V-intercept of the graph? Answer: The V-intercept is 30.

What values of t 1 and V are meaningful in the context of the problem? Answer: In the problem context, time and velocity are positive values. Therefore, positive values of t 1 and V values between 30 and 60 are meaningful.

Transportation A train travels at one velocity V 1 for a given amount of time t 1 and then another velocity V 2 for a different amount of time t 2. The average velocity is given by a. Let t 1 be the independent variable and let V be the dependent variable. Draw the graph if V 1 = 60 miles per hour, V 2 = 30 miles per hour, and t 2 = 1 hour.
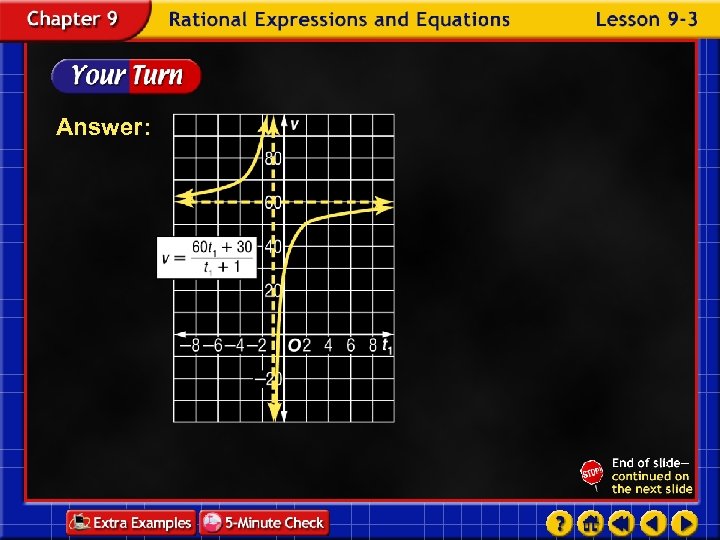
Answer:
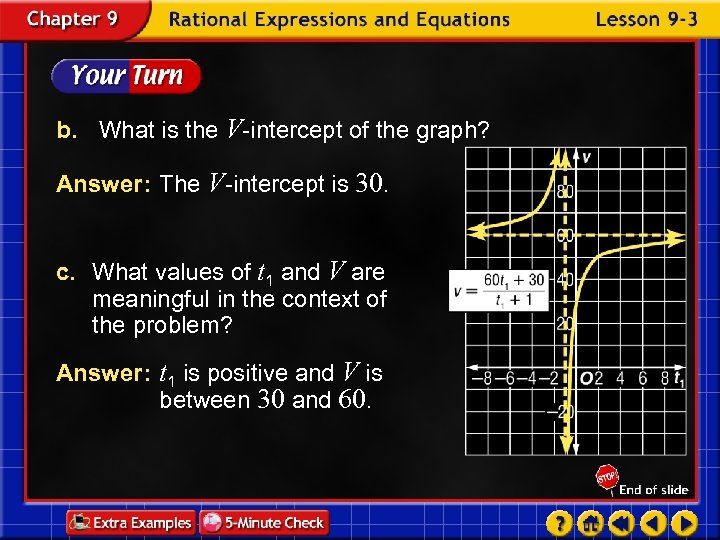
b. What is the V-intercept of the graph? Answer: The V-intercept is 30. c. What values of t 1 and V are meaningful in the context of the problem? Answer: t 1 is positive and V is between 30 and 60.

Example 1 Direct Variation Example 2 Joint Variation Example 3 Inverse Variation Example 4 Use Inverse Variation

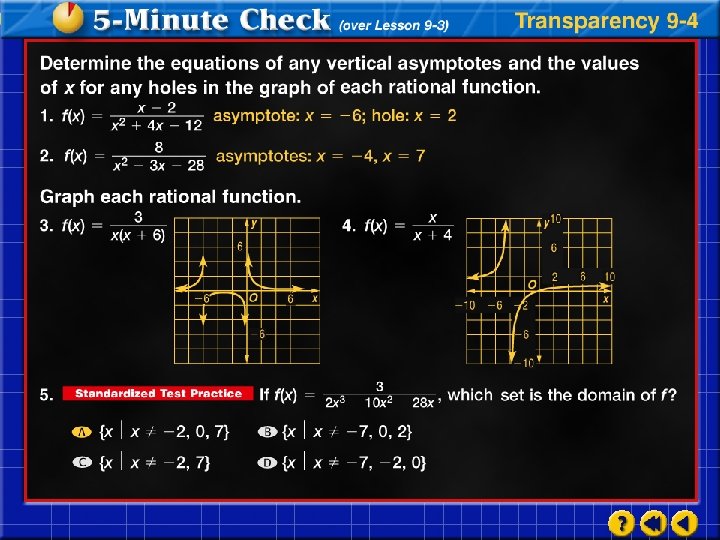
If y varies directly as x and y = – 15 when x = 5, find y when x = 3. Use a proportion that relates the values. Direct proportion y 1 = – 15; x 1 = 5, and x 2 = 3 Cross multiply.
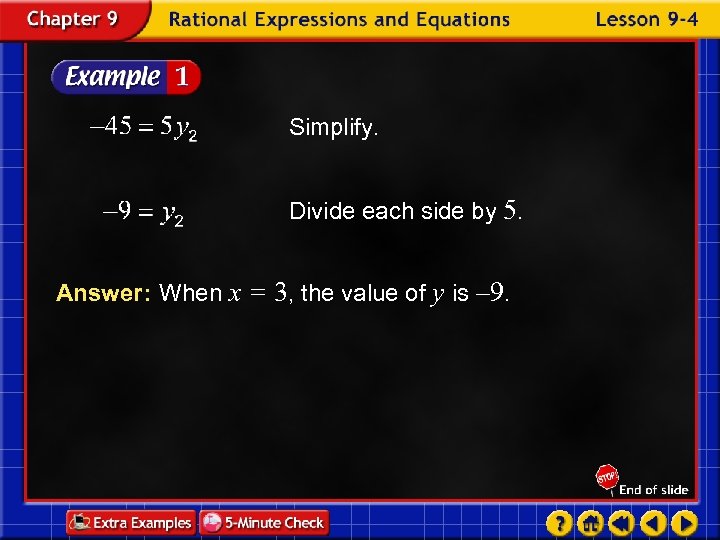
Simplify. Divide each side by 5. Answer: When x = 3, the value of y is – 9.
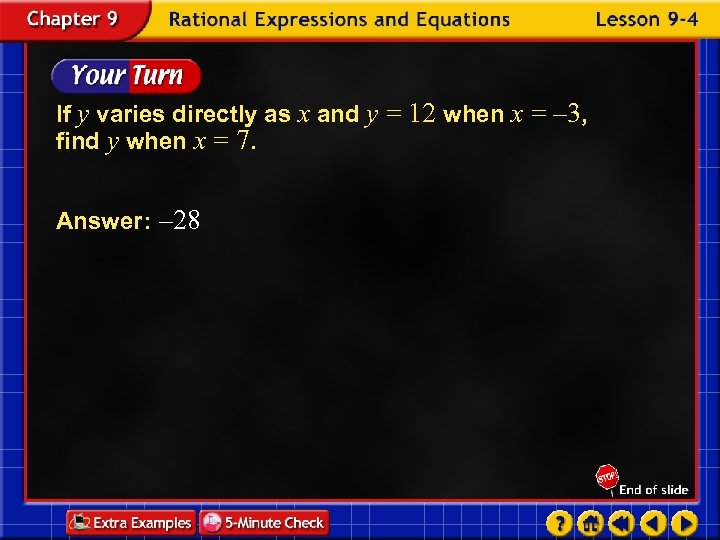
If y varies directly as x and y = 12 when x = – 3, find y when x = 7. Answer: – 28
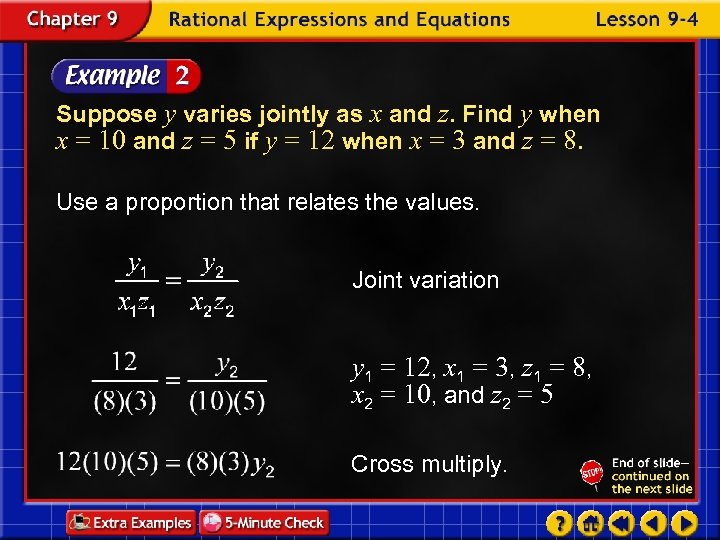
Suppose y varies jointly as x and z. Find y when x = 10 and z = 5 if y = 12 when x = 3 and z = 8. Use a proportion that relates the values. Joint variation y 1 = 12, x 1 = 3, z 1 = 8, x 2 = 10, and z 2 = 5 Cross multiply.
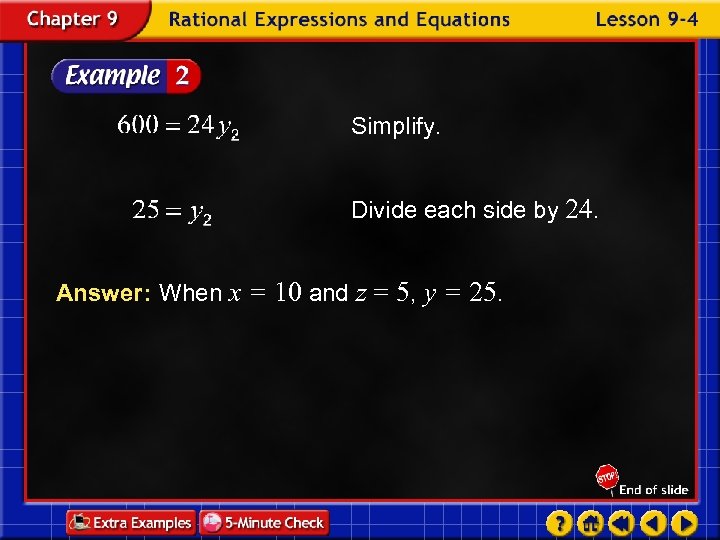
Simplify. Divide each side by 24. Answer: When x = 10 and z = 5, y = 25.
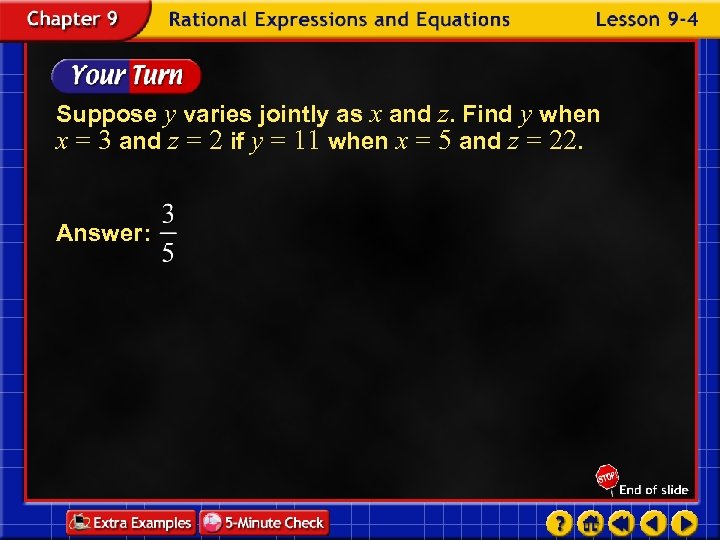
Suppose y varies jointly as x and z. Find y when x = 3 and z = 2 if y = 11 when x = 5 and z = 22. Answer:
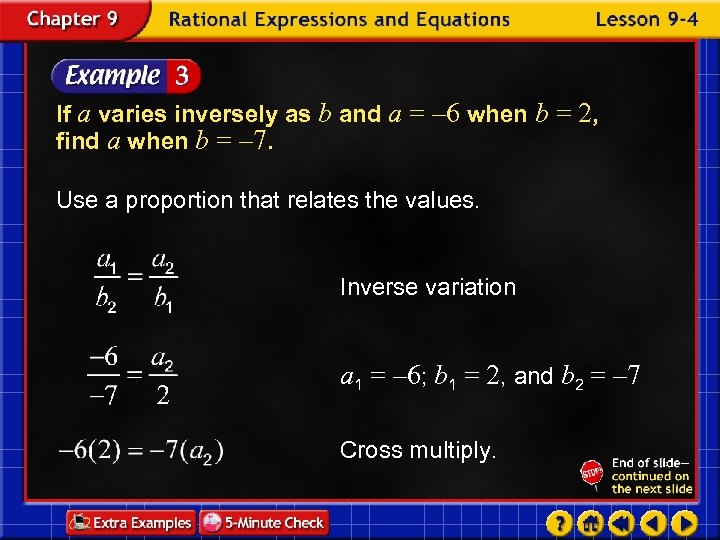
If a varies inversely as b and a = – 6 when b = 2, find a when b = – 7. Use a proportion that relates the values. Inverse variation a 1 = – 6; b 1 = 2, and b 2 = – 7 Cross multiply.
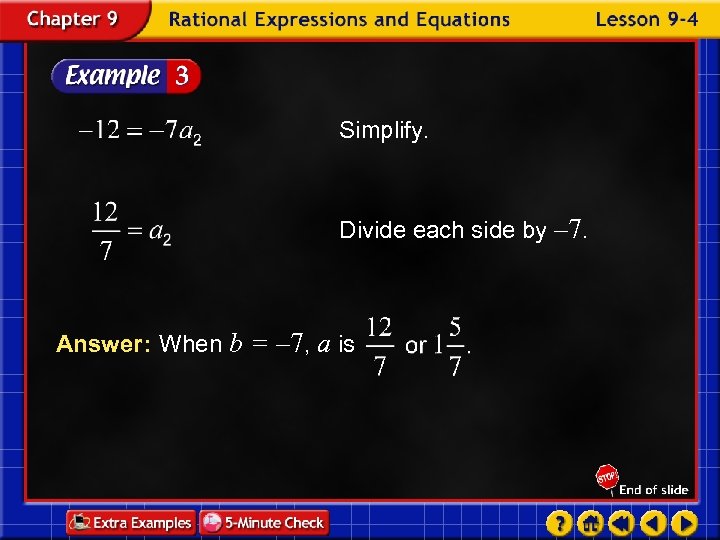
Simplify. Divide each side by – 7. Answer: When b = – 7, a is
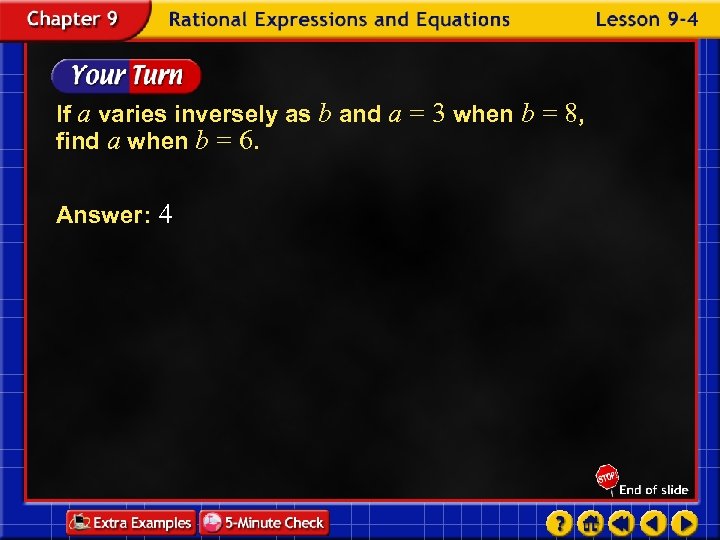
If a varies inversely as b and a = 3 when b = 8, find a when b = 6. Answer: 4

Space The apparent length of an object is inversely proportional to one’s distance from the object. Earth is about 93 million miles from the Sun and Venus is about 67 million miles away. How much larger would the diameter of the Sun appear on Venus than on Earth? Explore You know that the apparent diameter of the Sun varies inversely with the distance from the Sun. You also know the distance from the Sun to Venus and from the Sun to Earth. You want to determine how much larger the diameter of the Sun appears on Venus than on Earth.
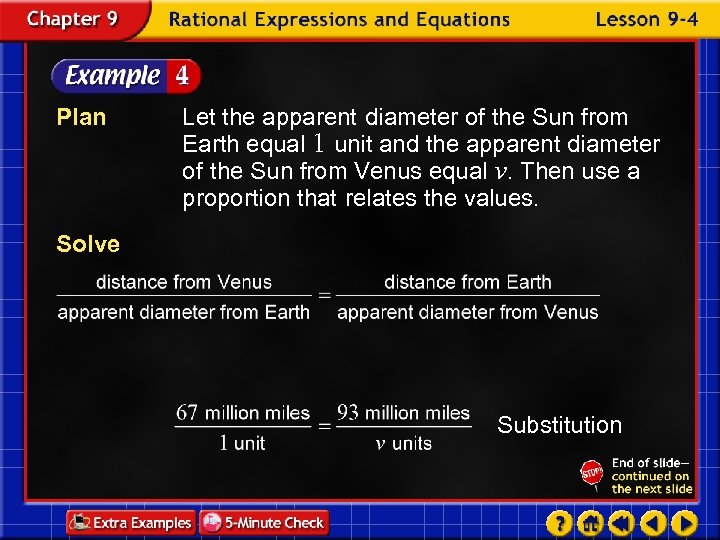
Plan Let the apparent diameter of the Sun from Earth equal 1 unit and the apparent diameter of the Sun from Venus equal v. Then use a proportion that relates the values. Solve Substitution
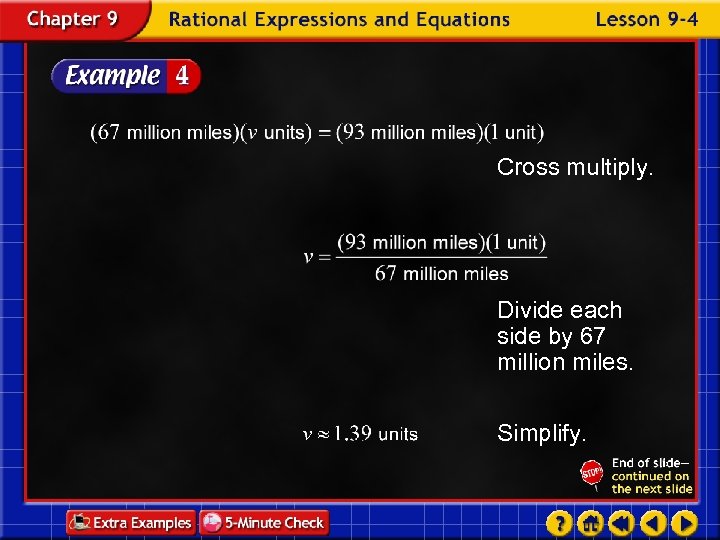
Cross multiply. Divide each side by 67 million miles. Simplify.

Answer: From Venus, the diameter of the Sun will appear about 1. 39 times as large as it appears from Earth. Examine Since the distance between the Sun and Earth is between 1 and 2 times the distance between the Sun and Venus, the answer seems reasonable.
Space Mars is about 142. 5 million miles from the Sun and Earth is about 93 million miles away. How much smaller would the diameter of the Sun appear on Mars than on Earth? Answer: about 0. 65 of the size

Example 1 Identify a Function Given the Graph Example 2 Match Equation with Graph Example 3 Identify a Function Given its Equation
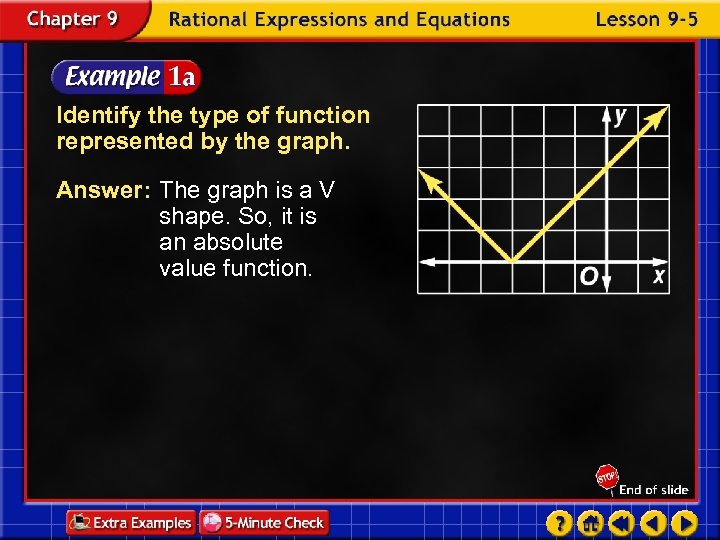
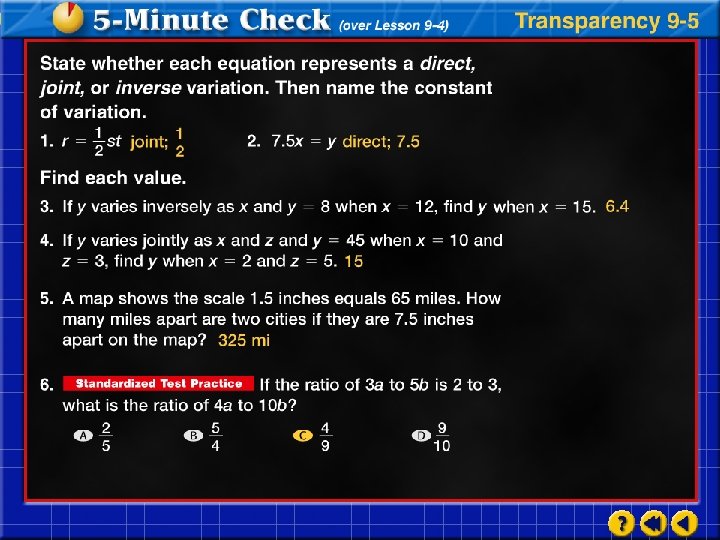
Identify the type of function represented by the graph. Answer: The graph is a V shape. So, it is an absolute value function.
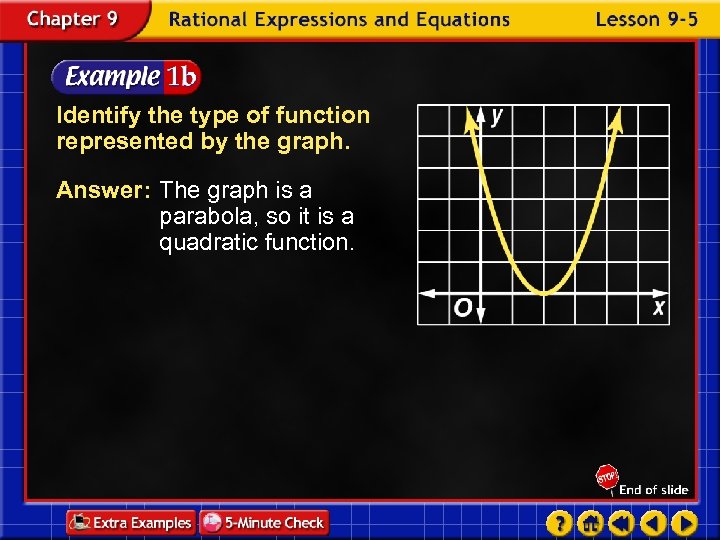
Identify the type of function represented by the graph. Answer: The graph is a parabola, so it is a quadratic function.
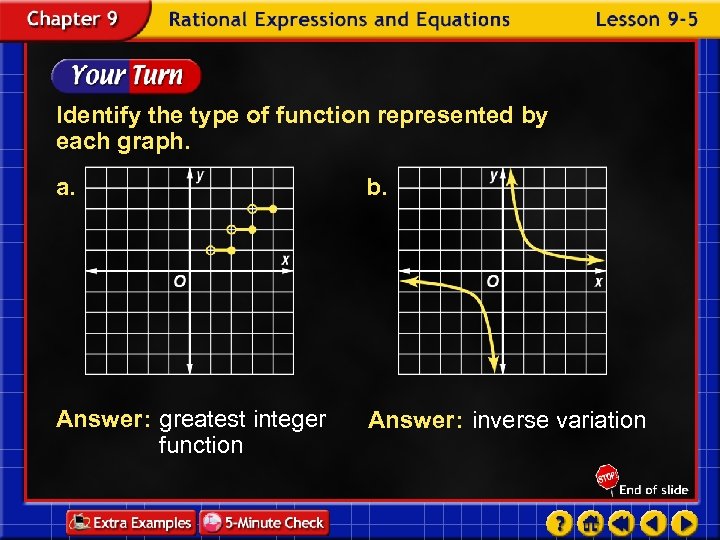
Identify the type of function represented by each graph. a. b. Answer: greatest integer function Answer: inverse variation
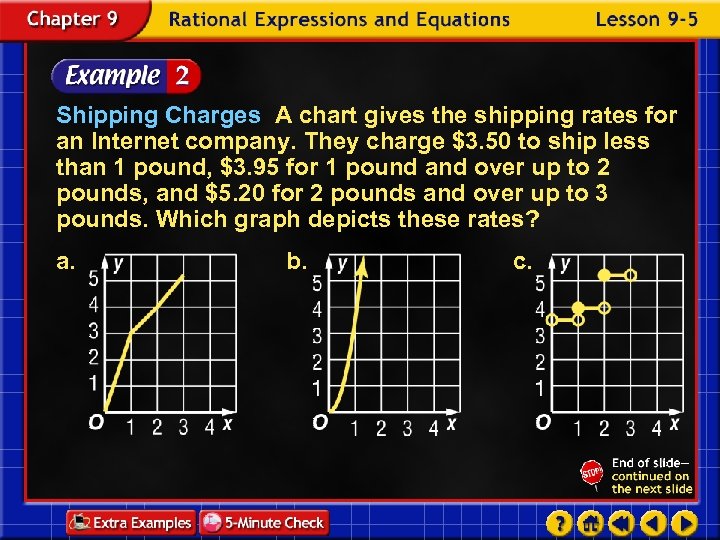
Shipping Charges A chart gives the shipping rates for an Internet company. They charge $3. 50 to ship less than 1 pound, $3. 95 for 1 pound and over up to 2 pounds, and $5. 20 for 2 pounds and over up to 3 pounds. Which graph depicts these rates? a. b. c.
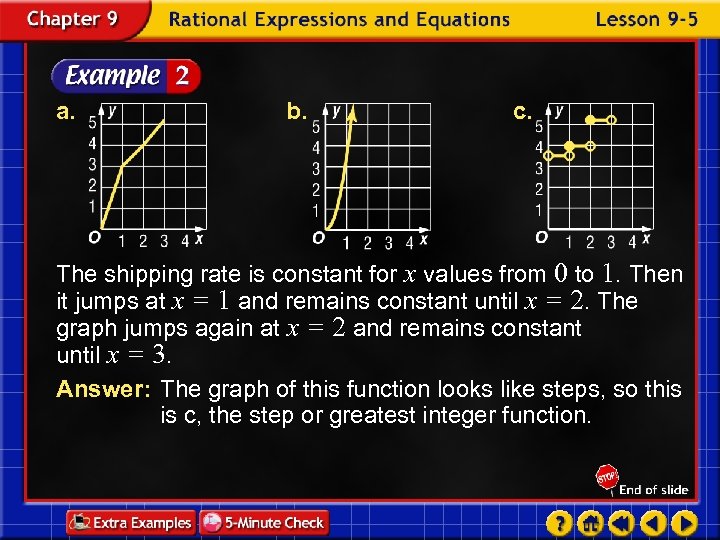
a. b. c. The shipping rate is constant for x values from 0 to 1. Then it jumps at x = 1 and remains constant until x = 2. The graph jumps again at x = 2 and remains constant until x = 3. Answer: The graph of this function looks like steps, so this is c, the step or greatest integer function.
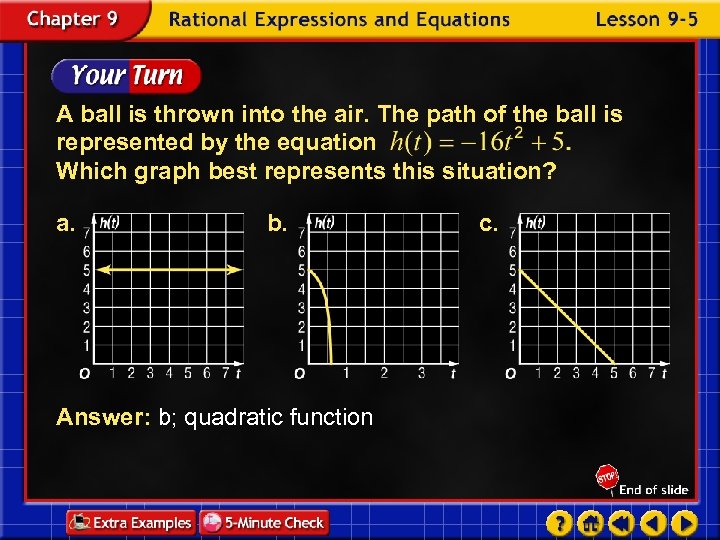
A ball is thrown into the air. The path of the ball is represented by the equation Which graph best represents this situation? a. b. Answer: b; quadratic function c.

Identify the type of function represented by Then graph the equation. Since the equation has no x-intercept, it is the constant function. Determine some points on the graph and graph it. Answer:

Identify the type of function represented by Then graph the equation. Since the equation includes an expression with a square root, it is a square root function. Plot some points and use what you know about square root graphs to graph it. Answer:

Identify the type of function represented by each equation. Then graph the equation. a. b. Answer: rational function direct variation

Example 1 Solve a Rational Equation Example 2 Elimination of a Possible Solution Example 3 Work Problem Example 4 Rate Problem Example 5 Solve a Rational Inequality
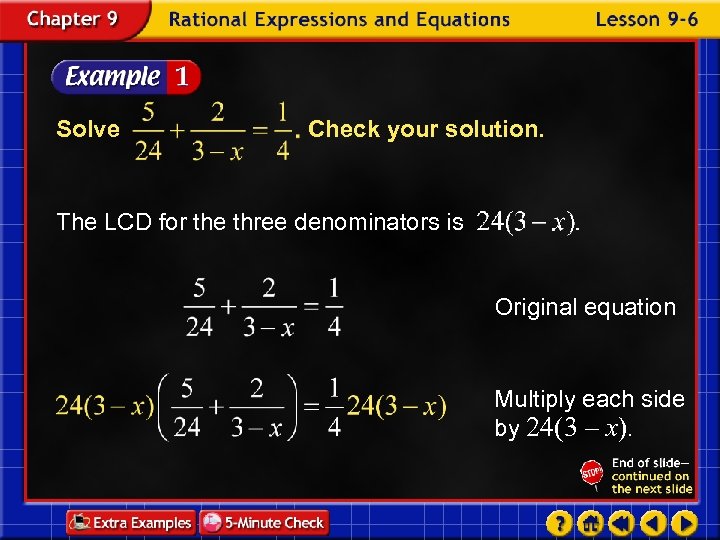
Solve Check your solution. The LCD for the three denominators is Original equation Multiply each side by 24(3 – x).
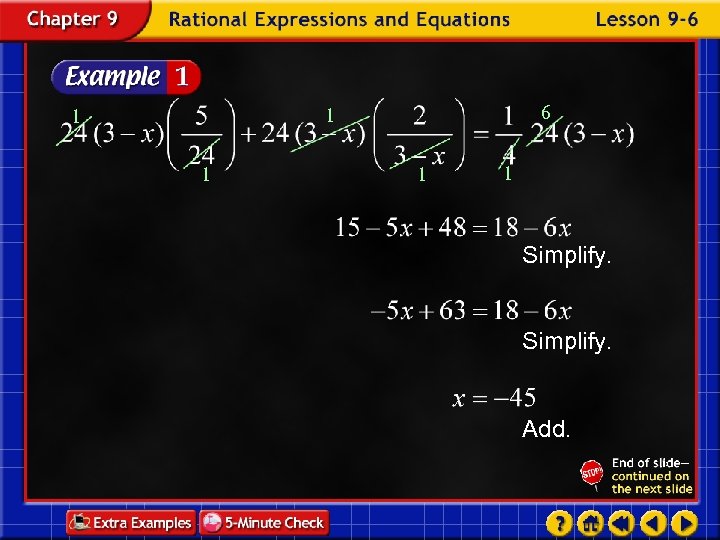
6 1 1 1 Simplify. Add.
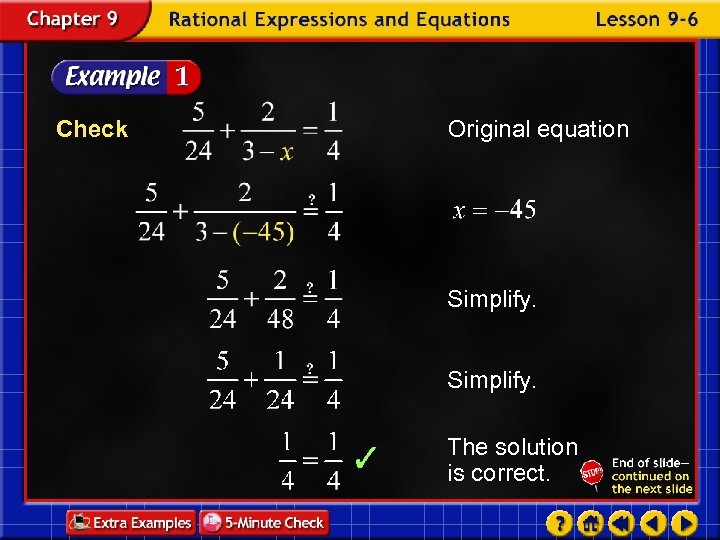
Check Original equation Simplify. The solution is correct.
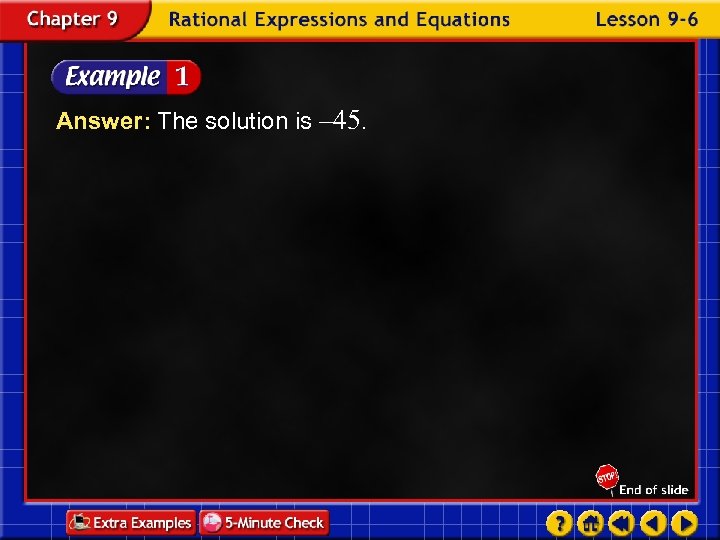
Answer: The solution is – 45.
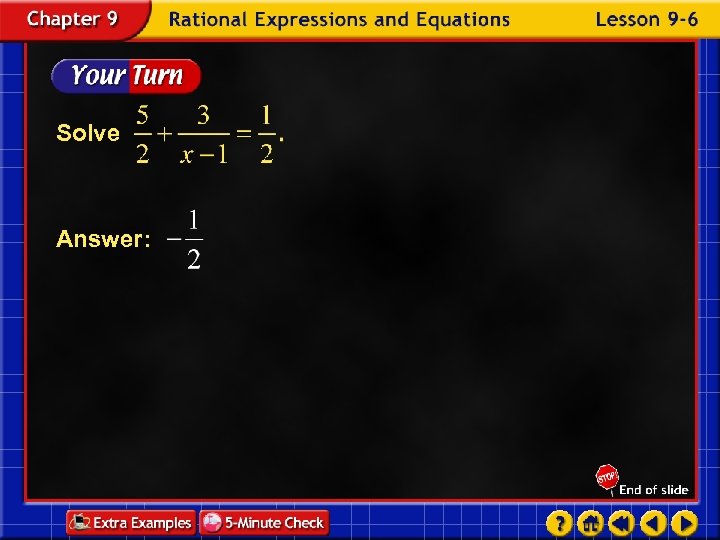
Solve Answer:

Solve Check your solution. The LCD is Original equation p– 1 1 Multiply by the LCD, (p 2 – 1).

Distributive Property Simplify. Add (2 p 2 – 2 p + 1) to each side.
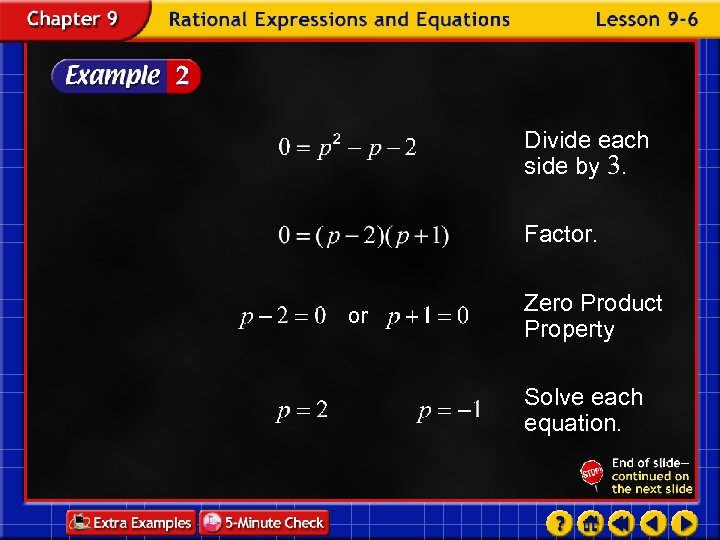
Divide each side by 3. Factor. or Zero Product Property Solve each equation.
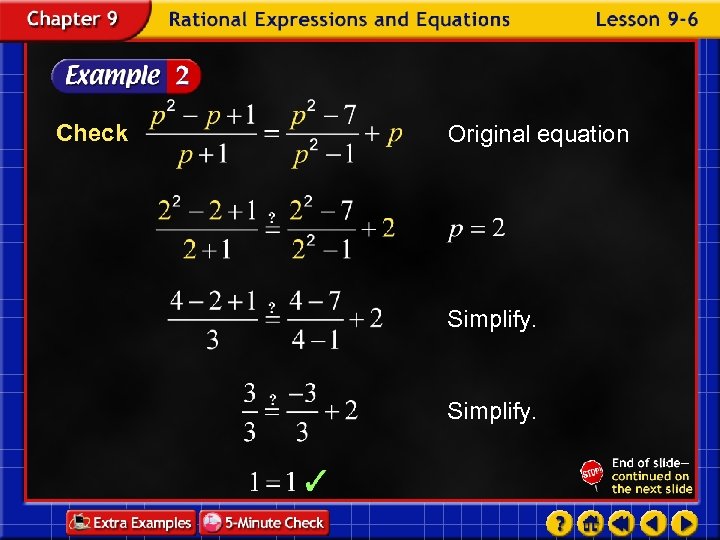
Check Original equation Simplify.
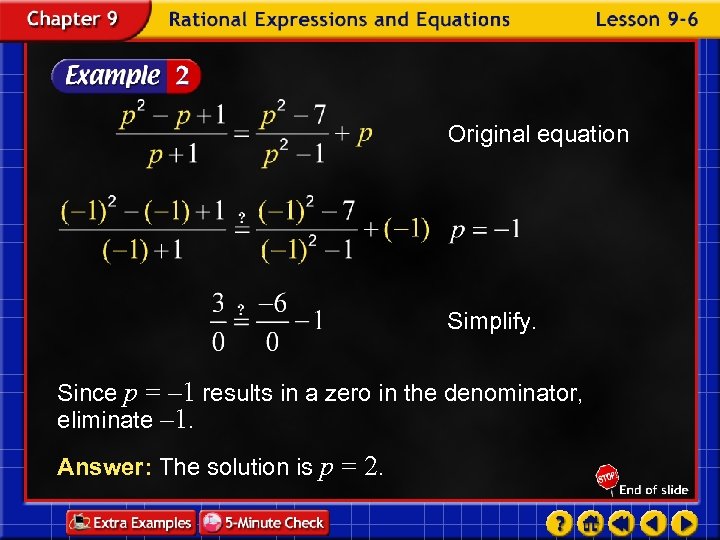
Original equation Simplify. Since p = – 1 results in a zero in the denominator, eliminate – 1. Answer: The solution is p = 2.
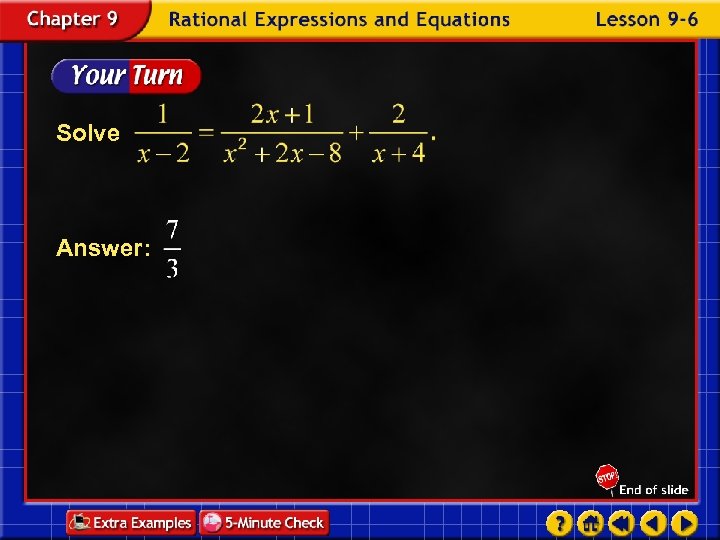
Solve Answer:

Mowing Lawns Tim and Ashley mow lawns together. Tim working alone could complete the job in 4. 5 hours, and Ashley could complete it alone in 3. 7 hours. How long does it take to complete the job when they work together? In 1 hour, Tim could complete In 1 hour, Ashley could complete of the job.

In t hours, Tim could complete In t hours, Ashley could complete Part completed by Tim plus part completed by Ashley or of the job. equals entire job. 1
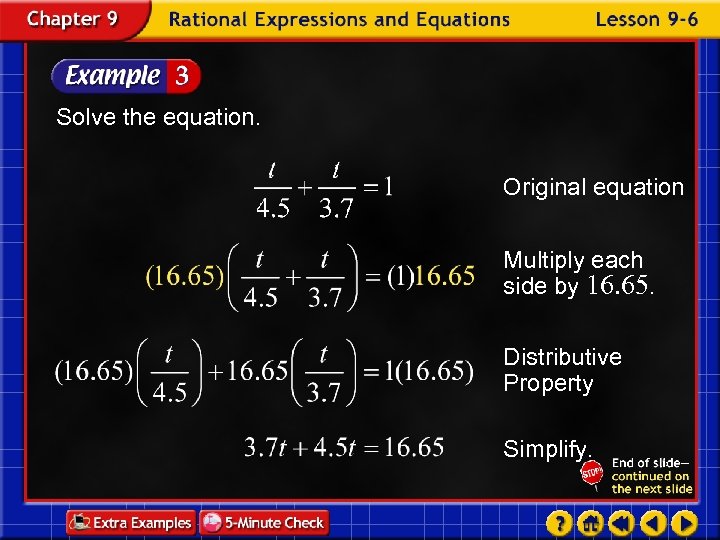
Solve the equation. Original equation Multiply each side by 16. 65. Distributive Property Simplify.
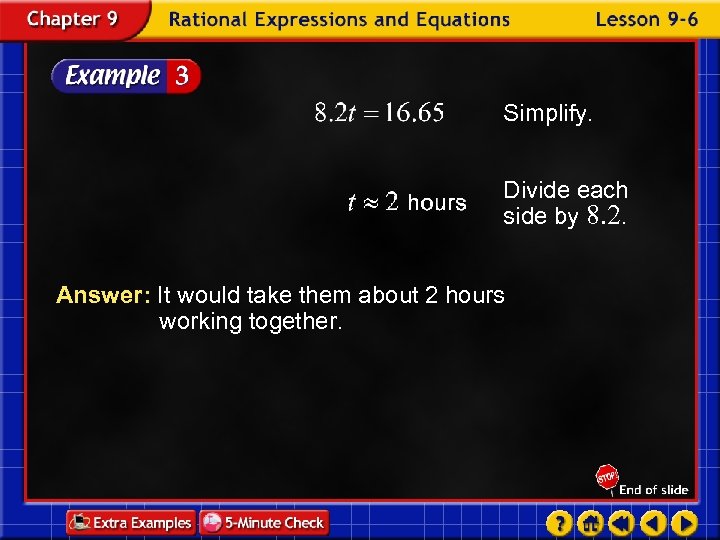
Simplify. Divide each side by 8. 2. Answer: It would take them about 2 hours working together.
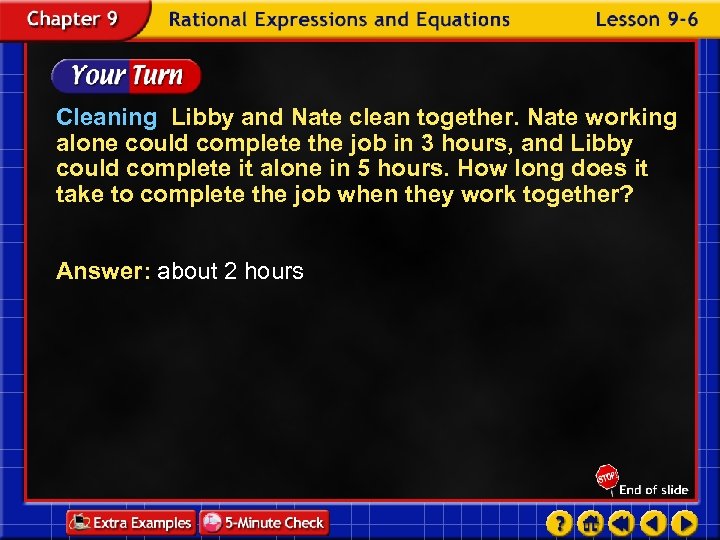
Cleaning Libby and Nate clean together. Nate working alone could complete the job in 3 hours, and Libby could complete it alone in 5 hours. How long does it take to complete the job when they work together? Answer: about 2 hours

Swimming Janine swims for 5 hours in a stream that has a current of 1 mile per hour. She leaves her dock and swims upstream for 2 miles and then back to her dock. What is her swimming speed in still water? Words The formula that relates distance, time, and rate is Variables Let r be her speed in still water. Then her speed with the current is r + 1 and her speed against the current is r – 1.

Time going with time going against total the current plus the current equals time. 5 Equation Solve the equation. Original equation
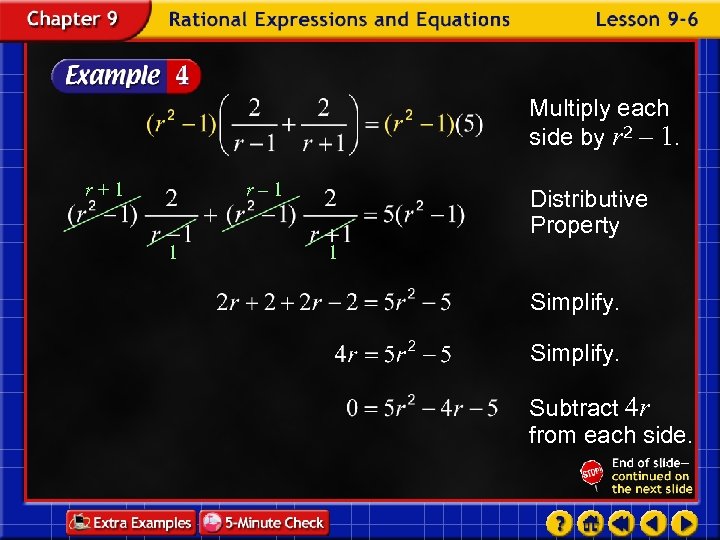
Multiply each side by r 2 – 1. r+1 r– 1 1 Distributive Property 1 Simplify. Subtract 4 r from each side.
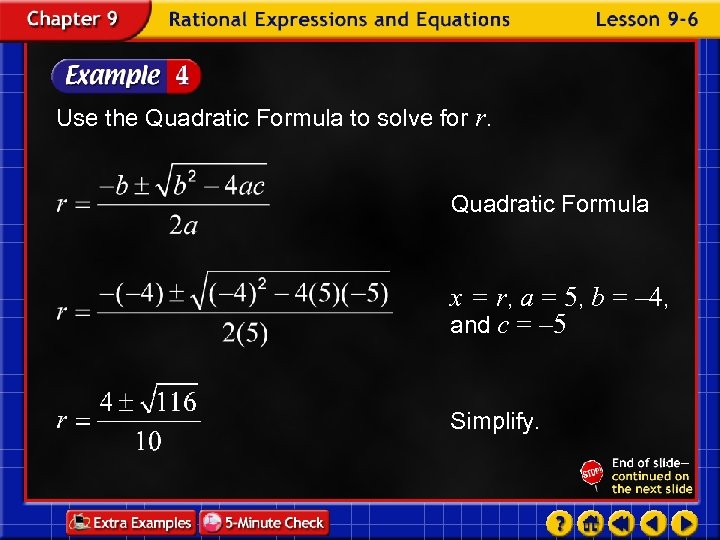
Use the Quadratic Formula to solve for r. Quadratic Formula x = r, a = 5, b = – 4, and c = – 5 Simplify.
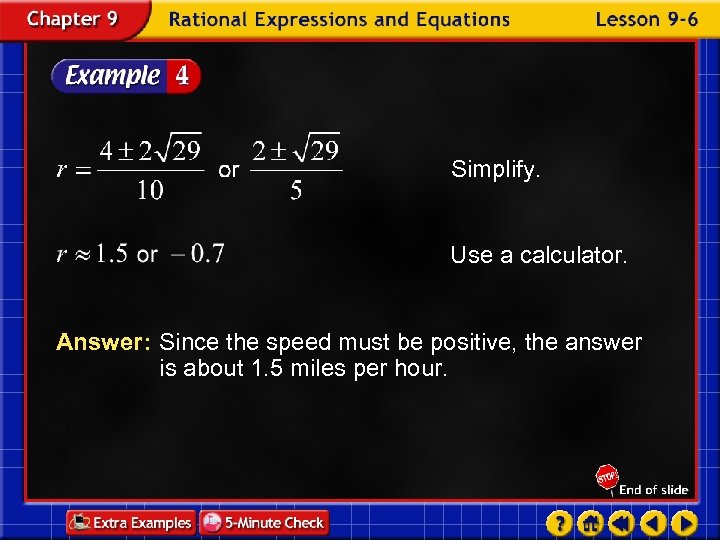
Simplify. Use a calculator. Answer: Since the speed must be positive, the answer is about 1. 5 miles per hour.
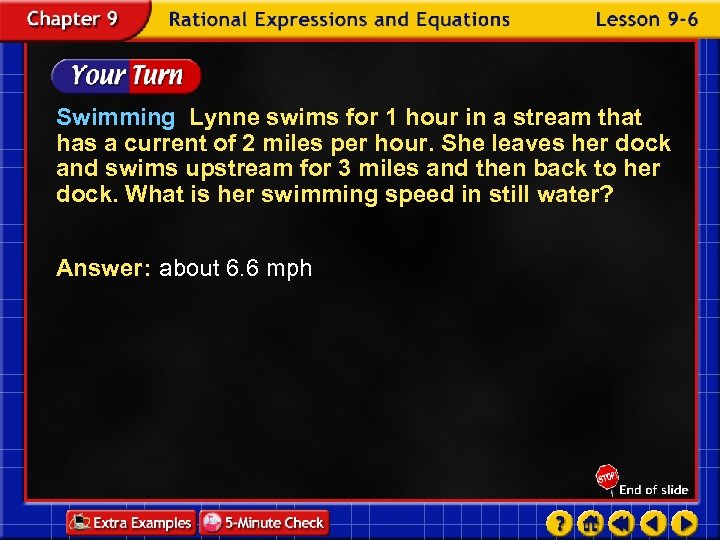
Swimming Lynne swims for 1 hour in a stream that has a current of 2 miles per hour. She leaves her dock and swims upstream for 3 miles and then back to her dock. What is her swimming speed in still water? Answer: about 6. 6 mph
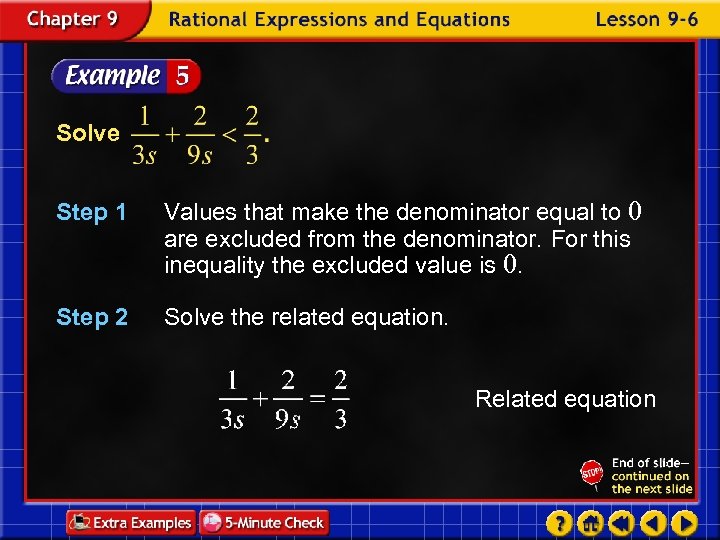
Solve Step 1 Values that make the denominator equal to 0 are excluded from the denominator. For this inequality the excluded value is 0. Step 2 Solve the related equation. Related equation
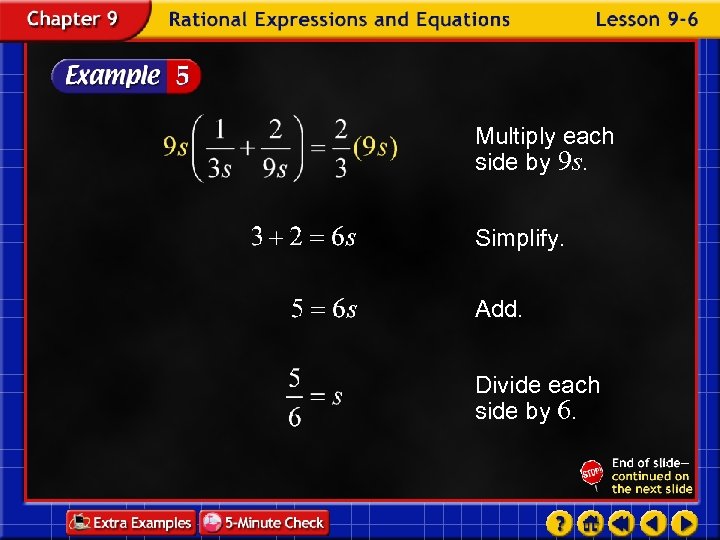
Multiply each side by 9 s. Simplify. Add. Divide each side by 6.

Step 3 Draw vertical lines at the excluded value and at the solution to separate the number line into regions. Now test a sample value in each region to determine if the values in the region satisfy the inequality.
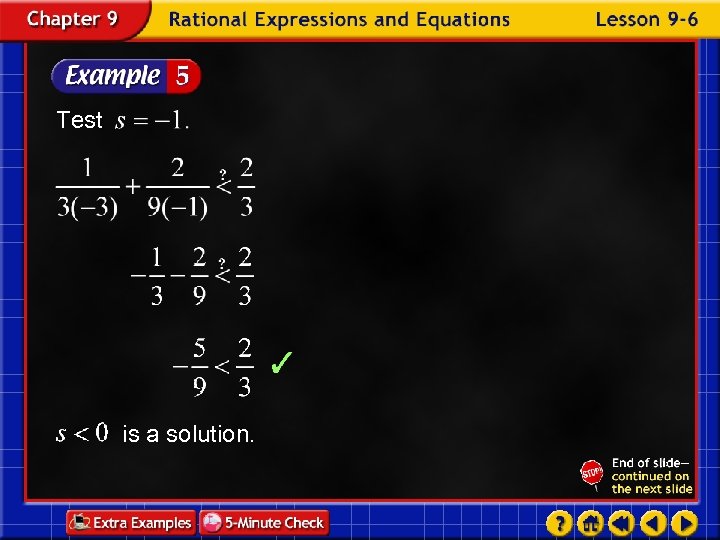
Test is a solution.
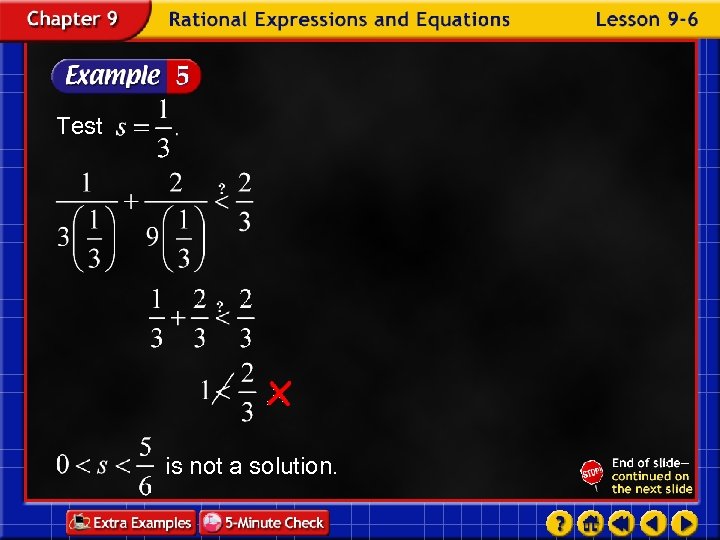
Test is not a solution.
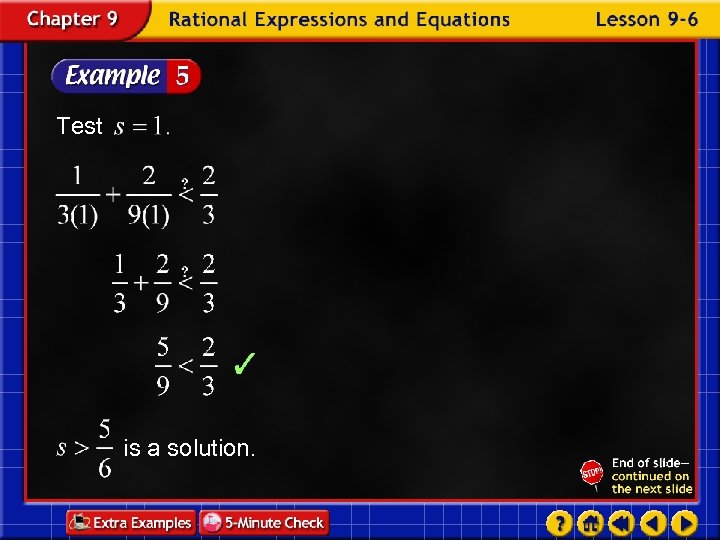
Test is a solution.
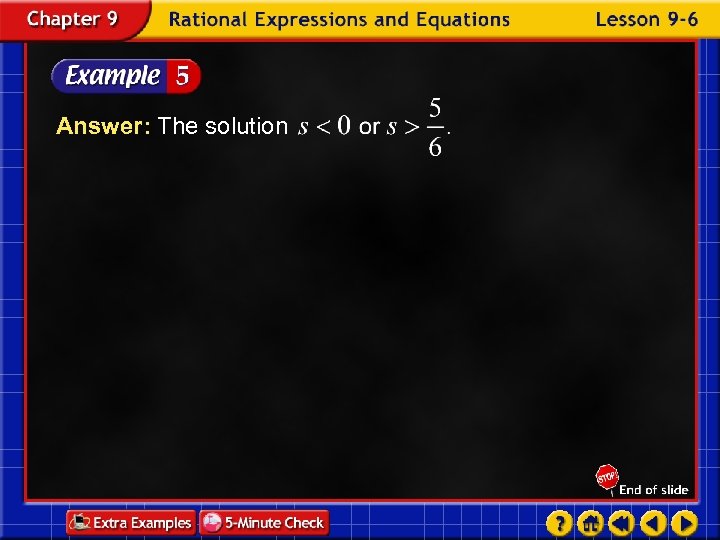
Answer: The solution
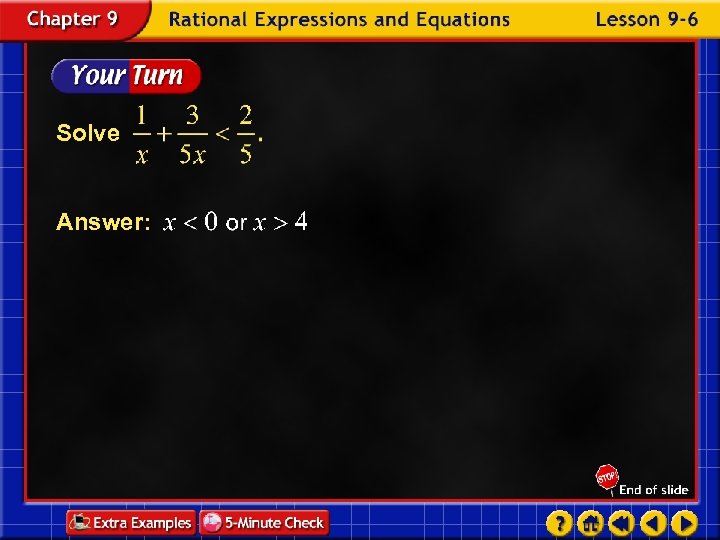
Solve Answer:


Explore online information about the information introduced in this chapter. Click on the Connect button to launch your browser and go to the Algebra 2 Web site. At this site, you will find extra examples for each lesson in the Student Edition of your textbook. When you finish exploring, exit the browser program to return to this presentation. If you experience difficulty connecting to the Web site, manually launch your Web browser and go to www. algebra 2. com/extra_examples.
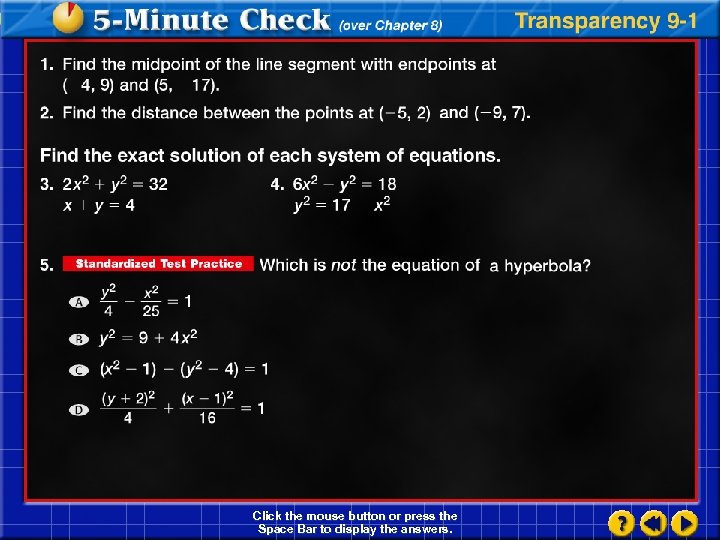
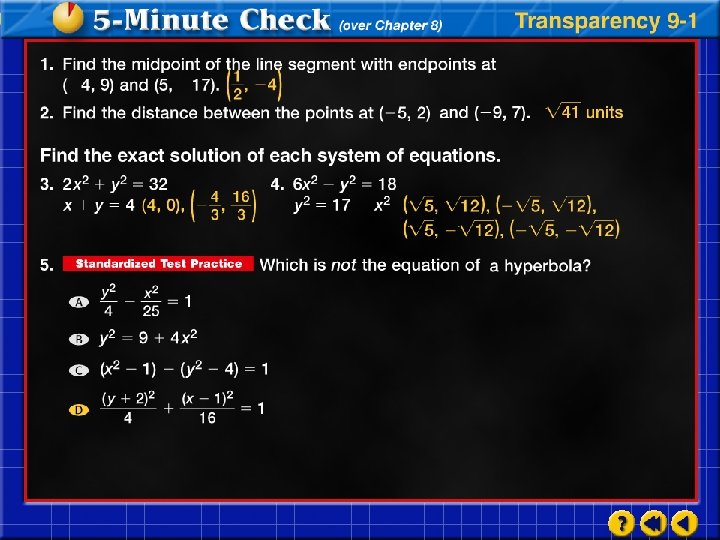
Click the mouse button or press the Space Bar to display the answers.
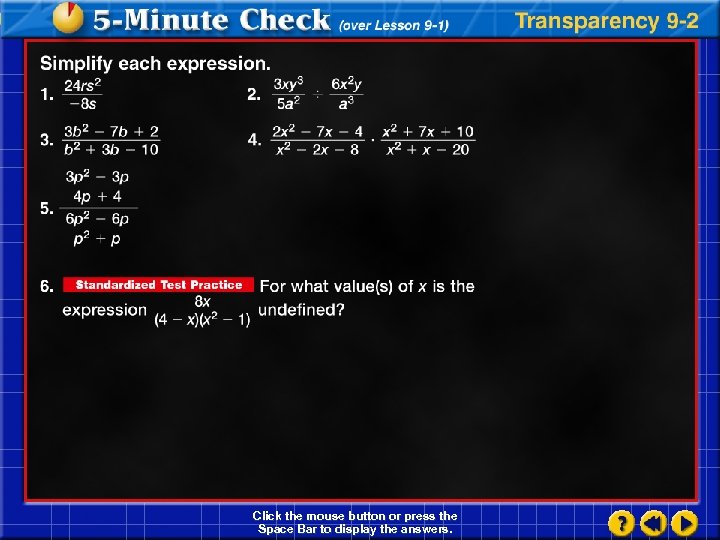
Click the mouse button or press the Space Bar to display the answers.
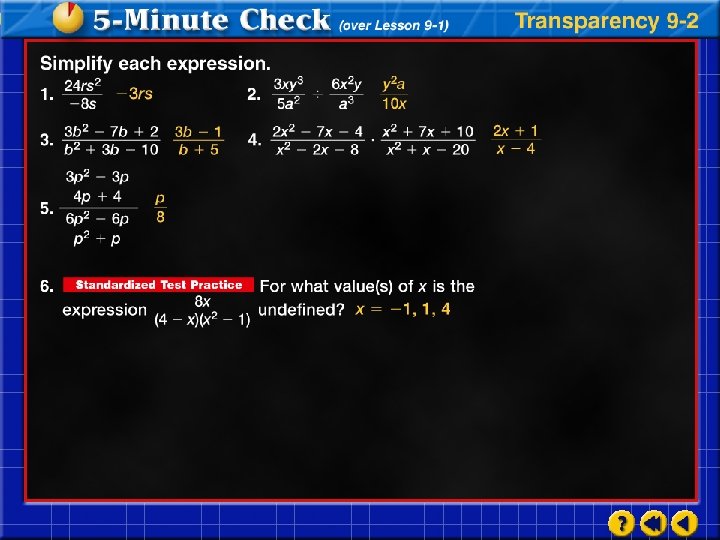

Click the mouse button or press the Space Bar to display the answers.
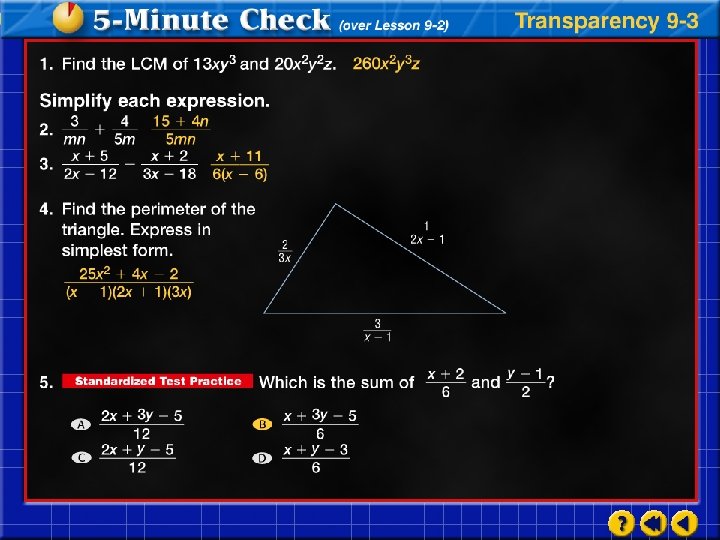
Click the mouse button or press the Space Bar to display the answers.

Click the mouse button or press the Space Bar to display the answers.
Click the mouse button or press the Space Bar to display the answers.

End of Custom Shows WARNING! Do Not Remove This slide is intentionally blank and is set to auto-advance to end custom shows and return to the main presentation.

d6fabb8f2e70fa02510a462a13b10174.ppt