Алексей Кислов МНОГОЗНАЧНАЯ ЛОГИКА Под многозначной логикой имеется

Алексей Кислов МНОГОЗНАЧНАЯ ЛОГИКА Под многозначной логикой имеется в виду раздел неклассической логики, который объединяет логические теории, основанные на принципе многозначности: всякое высказывание (формула) имеет более чем два возможных значения истинности. Другое название – поливалентные логики.

Хронология: с 1907 - идея интуиционистской математики Л. Э. Я. Брауэра с 1910 - «Воображаемая логика» Н. А. Васильева с 1920 - многозначные логики Я. Лукасевича и Э. Поста 1920 - статья И. Е. Орлова по релевантной логике 1925 – логико-конструктивистская статья А. Н. Колмогорова с 1930 - аксиоматизация интуиционистской логики А. Гейтингом 1930 -1960 - бурное развитие интуиционистской логики, а также «философских» (модальных и интенсиональных) логик 1968 – результат В. А. Янкова (семейство суперинтуиционистских логик = семейство всех расширений модальной логики S 4, представляет собой континуум) 1971 – теорема А. В. Кузнецова о континуальности всякого интервала между интуиционистской логикой и её собственным расширением

Ход рассуждений Аристотеля можно (не вполне формально) реконструировать следующим образом: пусть р – высказывание «Завтра произойдёт событие s» , причём s – случайное событие, тогда 1. (р истинно) (р ложно) – гипотеза (принцип двузначности) 2. s случайно – гипотеза 3. (р истинно) (s неизбежно произойдёт) 4. (р ложно) (s неизбежно не произойдёт) 5. (s неизбежно произойдёт) (s неизбежно не произойдёт) – из 1, 3 и 4 (сложная конструктивная дилемма) 6. (s случайно) – из 5 7. ((р истинно) (р ложно)) – из 2 и 6 (введение отрицания) - Лукасевич Я. О детерминизме // Логические исследования. Вып. 2. М. , 1993. С. 190– 205. (Переиздано в: Вопросы философии. 1995. № 5. С. 60– 71). - Карпенко А. С. Фатализм и случайность будущего: логический анализ. М. , 1990.

Философы-джайнисты принимали принцип семизначности, полагая, что высказывание может иметь одно из следующих семи значений: - «только истинно» , - «только ложно» , - «только неопределённо» , - «истинно и ложно» ( «противоречиво» или «невозможно» ), - «истинно и неопределённо» ( «скорее истинно» ), - «ложно и неопределённо» ( «скорее ложно» ), - «истинно, ложно и неопределённо» ( «неизвестно» или «безразлично» ).

Независимость аксиомы А: А не есть теорема в системе, получающейся посредством исключения А из числа аксиом, т. е. А S независима в системе аксиом S ( S/{A} A) Для доказательства независимости аксиомы А следует подобрать такую истинностную таблицу с выделенным(-и) значением(-ями), в которой - все правила вывода обладают свойством сохранять выделенное значение (тавтологию), и - все аксиомы, кроме А, получают выделенное значение (являются тавтологиями). Отсюда следует, что аксиома А, которая не является в заданной таблицей интерпретации формулой-тавтологией, независима от остальных аксиом системы.

В качестве примера рассмотрим исчисление Pλ классической логики высказываний с полным функциональным набором < , >, встречающееся в Чёрч А. «Введение в математическую логику» (М. , 1960): Две схемы аксиом: A. 1. ((A B) C) ((C A) (D A)) A. 2. A Правило вывода: (MP) A, A B B Возьмём следующую трёхзначную таблицу для импликации с 1 в качестве выделенного значения: Очевидно: MP - сохраняет тавтологию; А. 2. – тавтология. В свою очередь А. 1. при A=½, B=0, C=½, D=1 – принимает значение ½, т. е. не тавтология. 1 ½ 0 1 1 ½ ½ 1 1 0 0 ½ 1

Трёхзначная логика Лукасевича – Ł3 Всякое высказывание – либо истинно, либо случайно, либо ложно. Эти три истинностных значения принято обозначать числами: 1 – «истина» , ½ – «случайность» , 0 – «ложь» . Значение пропозициональным связкам по-прежнему задают посредством сопоставления с определёнными истинностноистинностными функциями вида f: {1, ½, 0}n {1, ½, 0}. Синтаксис прежний: Атомарные формулы: p Ф 0 Формулы: А Ф А: : = р | А В

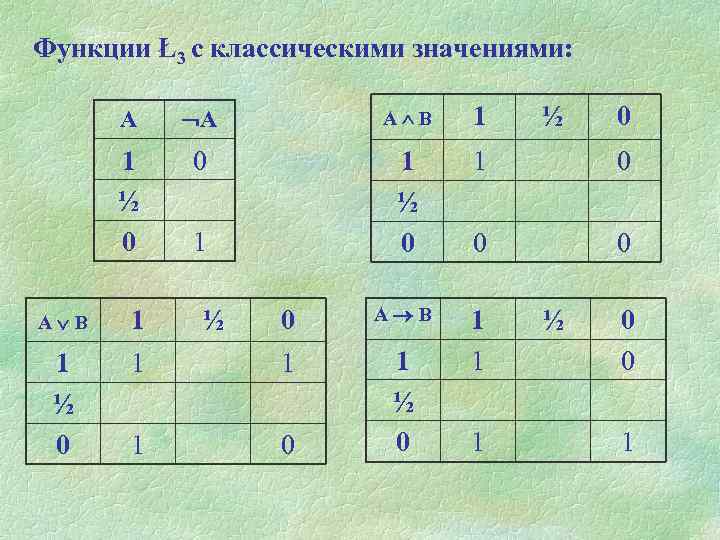Функции Ł3 с классическими значениями: А А А В 1 1 ½ 0 0 1 ½ 0 1 0 0 А В 1 ½ 0 1 1 1 0 1 ½ ½ 0 0 0 1

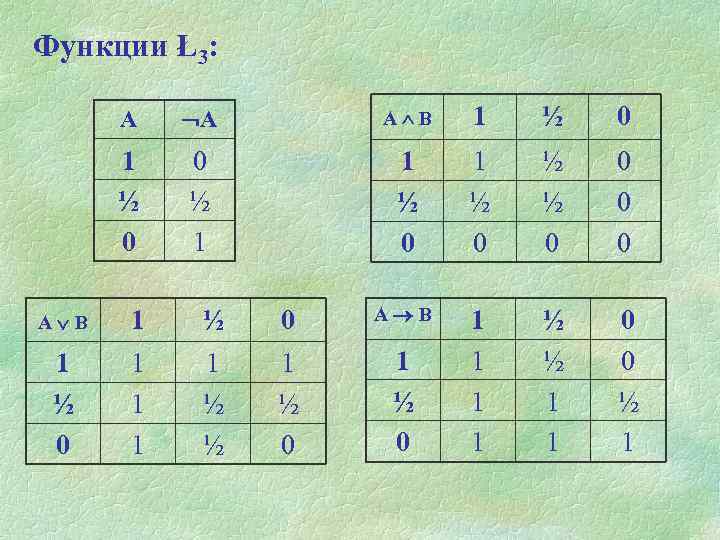Функции Ł3: А А А В 1 ½ 0 0 ½ 1 1 ½ 0 ½ ½ 0 0 1 1 ½ ½ 1 1 0 0 ½ 1 А В 1 ½ 0 1 1 ½ ½ 1 ½ 0

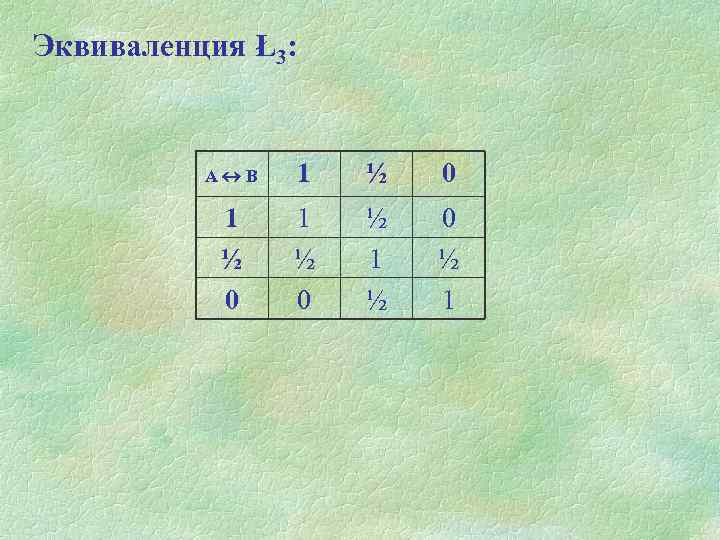Эквиваленция Ł3: А В 1 ½ 0 ½ 1

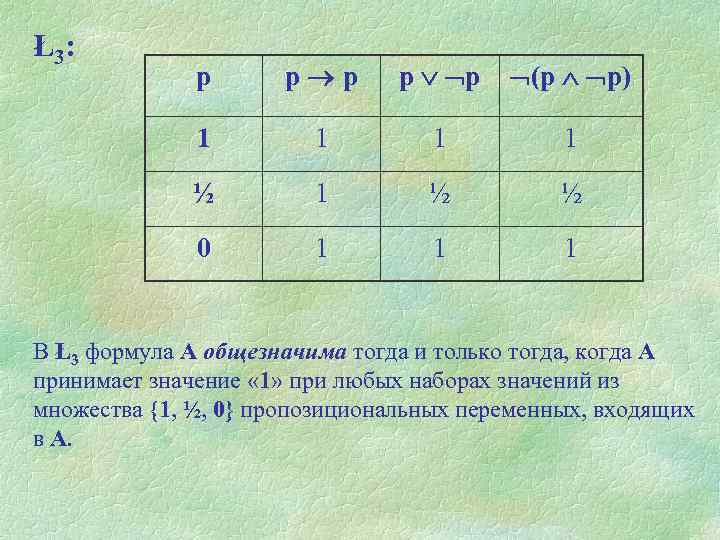Ł3: р р р (р р) 1 1 ½ 1 ½ ½ 0 1 1 1 В Ł3 формула А общезначима тогда и только тогда, когда А принимает значение « 1» при любых наборах значений из множества {1, ½, 0} пропозициональных переменных, входящих в А.

Отношение между множествами законов классической логики высказываний (PL 2) и Ł3, заданных в языке со стандартными связками , , , таково: всякая общезначимая в Ł3 формула является законом PL 2, но не наоборот, т. е. Ł3 А PL 2 А

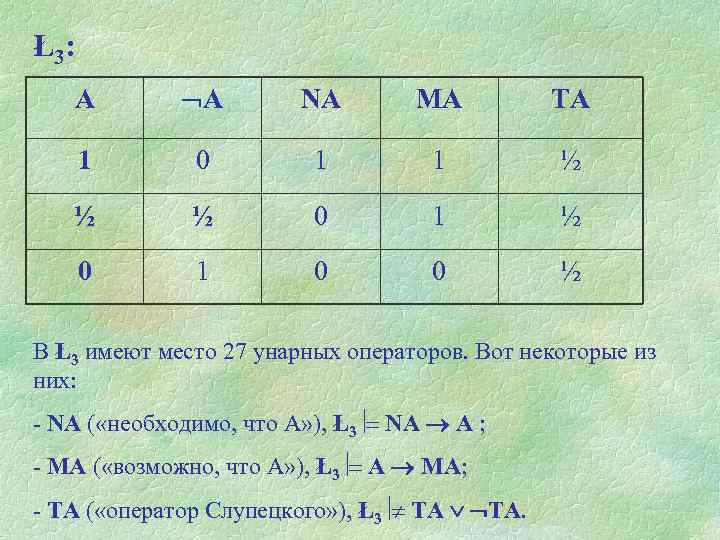Ł3: A A NA MA TA 1 0 1 1 ½ ½ ½ 0 1 0 0 ½ В Ł3 имеют место 27 унарных операторов. Вот некоторые из них: - NA ( «необходимо, что А» ), Ł3 NА А ; - МA ( «возможно, что А» ), Ł3 А МА; - ТA ( «оператор Слупецкого» ), Ł3 ТA.

Однако, можно сформулировать логику Ł*3, где формула А общезначима тогда и только тогда, когда А принимает значение из множества {1, ½} при любых наборах значений из множества {1, ½, 0} пропозициональных переменных, входящих в А. В Ł*3 общезначимыми станут (отброшенные ранее) следующие формулы: р (р р) р р Тр 1 1 1 ½ ½ ½ 0 1 1 ½

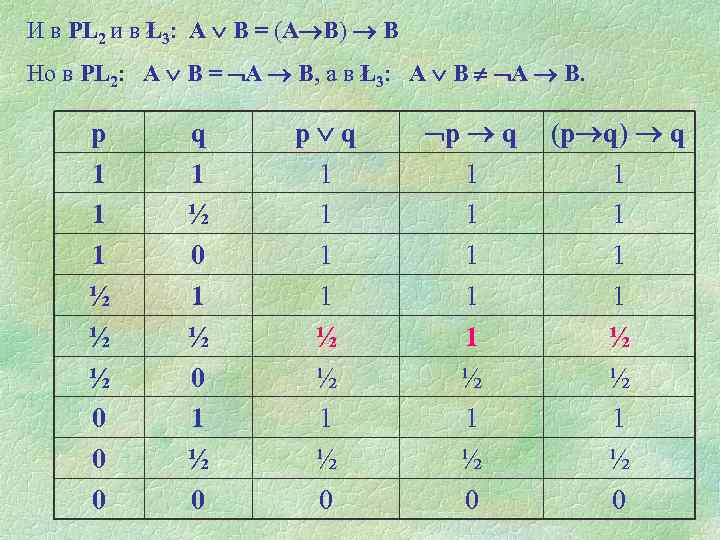И в PL 2 и в Ł3: А В = (А В) В Но в PL 2: А В = А В, а в Ł3: А В. р 1 1 1 ½ ½ ½ 0 0 0 q 1 ½ 0 p q 1 1 ½ ½ 1 ½ 0 p q 1 1 1 ½ 0 (p q) q 1 1 ½ ½ 1 ½ 0

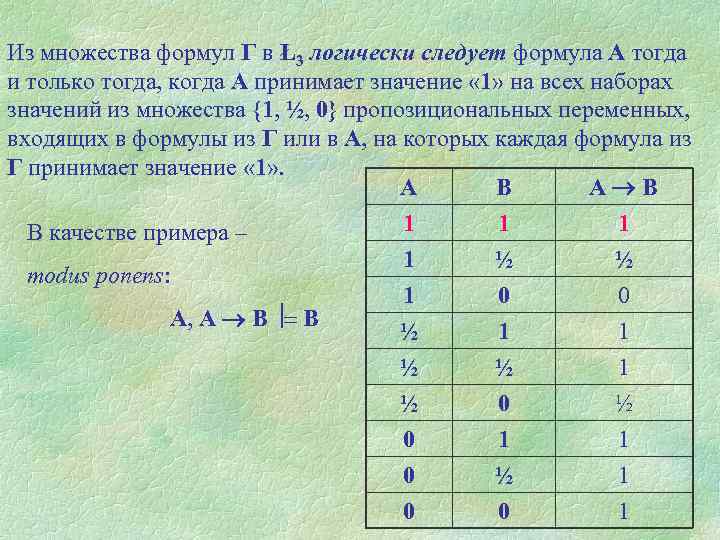Из множества формул Г в Ł3 логически следует формула А тогда и только тогда, когда А принимает значение « 1» на всех наборах значений из множества {1, ½, 0} пропозициональных переменных, входящих в формулы из Г или в А, на которых каждая формула из Г принимает значение « 1» . А В 1 1 1 В качестве примера – 1 ½ ½ modus ponens: 1 0 0 А, А В В ½ 1 1 ½ ½ 1 ½ 0 1 1 0 ½ 1 0 0 1

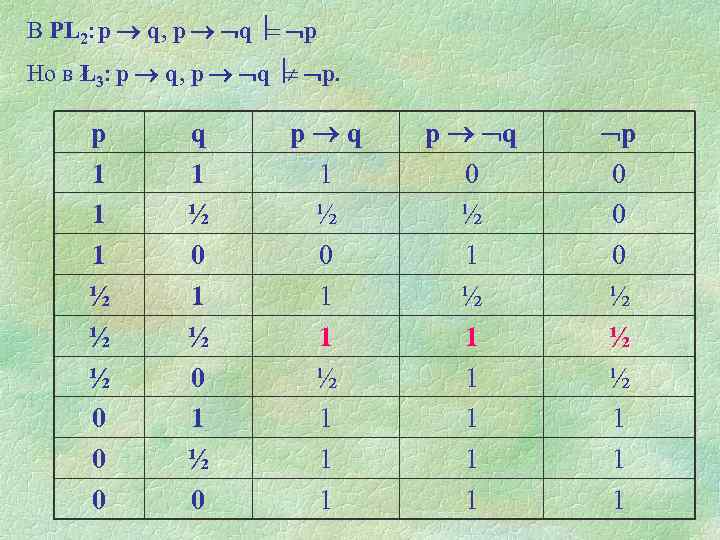В PL 2: p q, p q p Но в Ł3: p q, p q p. р 1 1 1 ½ ½ ½ 0 0 0 q 1 ½ 0 p q 1 ½ 0 1 1 ½ 1 1 1 p q 0 ½ 1 1 1 p 0 0 0 ½ ½ ½ 1 1 1

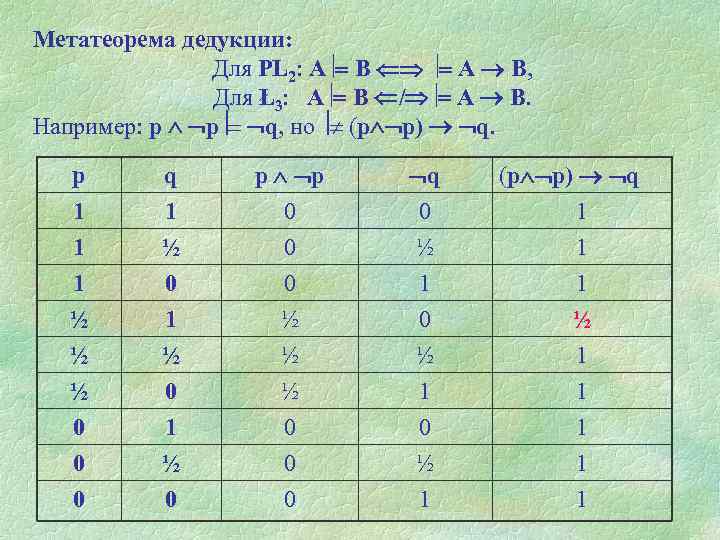Метатеорема дедукции: Для PL 2: А В, Для Ł3: А В / А В. Например: p p q, но (p p) q. р 1 1 1 q 1 ½ 0 p p 0 0 0 q 0 ½ 1 ½ ½ ½ 0 0 0 1 ½ 0 ½ ½ ½ 0 0 ½ 1 (p p) q 1 1 1 ½ 1 1 1

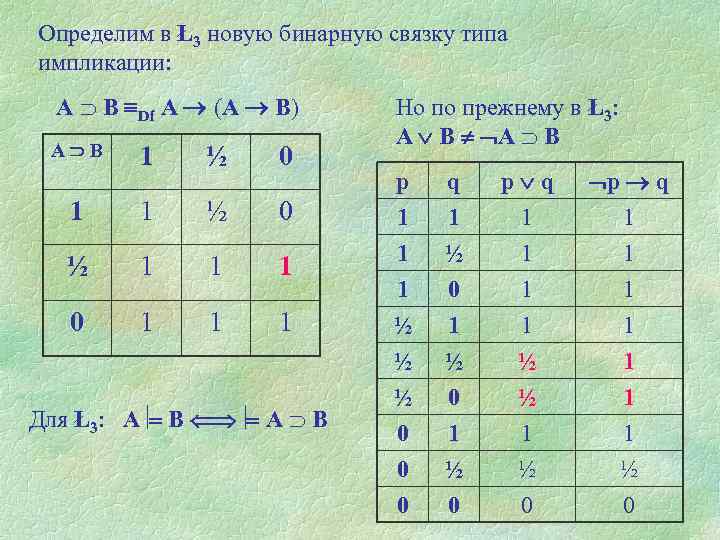Определим в Ł3 новую бинарную связку типа импликации: А В Df А (А В) А В 1 ½ 0 1 1 ½ 0 ½ 1 1 1 0 1 1 1 Для Ł3: А В Но по прежнему в Ł3: А В р 1 1 1 q 1 ½ 0 p q 1 1 1 p q 1 1 1 ½ ½ ½ 0 0 0 1 ½ ½ 1 ½ 0 1 1 ½ 0

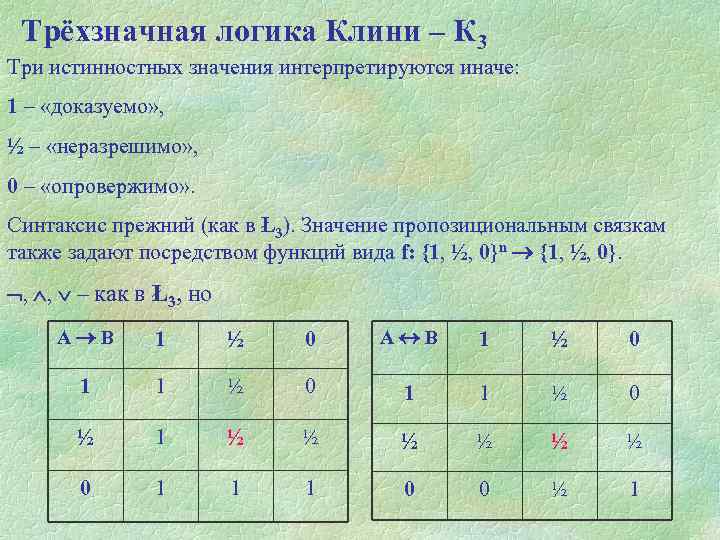Трёхзначная логика Клини – К 3 Три истинностных значения интерпретируются иначе: 1 – «доказуемо» , ½ – «неразрешимо» , 0 – «опровержимо» . Синтаксис прежний (как в Ł3). Значение пропозициональным связкам также задают посредством функций вида f: {1, ½, 0}n {1, ½, 0}. , , – как в Ł3, но А В 1 ½ 0 1 1 ½ 0 ½ 1 ½ ½ ½ 0 1 1 1 0 0 ½ 1

При приписывании каждой пропозициональной переменной значения «½» произвольная формула К 3 примет значение «½» . Если в К 3 « 1» – единственное выделенное значение, то: А К 3 А, т. е. класс общезначимых выражений К 3 пуст. Однако: К 3 Г А PL 2 Г А Если в К*3 « 1» и «½» – выделенные значения, то: К*3 А PL 2 А, т. е. К*3 и PL 2 дедуктивно эквивалентны (хотя семантически и различны). Ł*3 этим свойством не обладает: PL 2 (р р) ( р р), но Ł*3 (р р) ( р р) – принимает значение « 0» приписывании р значения «½» .

Трёхзначная логика Поста – Р’ 3 Три истинностных значения не интерпретируются содержательно, но « 1» – единственное выделенное значение (т. е. «истина» ). Синтаксис прежний. Значение пропозициональным связкам также задают посредством функций вида f: {1, ½, 0}n {1, ½, 0}. , , , – как в Ł3, но отрицание не «диагональное» как в Ł3, а «циклическое» . А 1 ½ 0 А ½ 0 1 Некоторые законы Р’ 3 не общезначимы в PL 2: (p p p)

Аксиоматизация Ł3 М. Вайсбергом – < , > и Е. Слупецким – <Т, , > Аксиомы: Ł31. p (q p) Ł32. (p q) ((q r) (p r)) Ł33. ( p q) (q p) Ł34. ((p p) p) p Ł35. Тp Тq Правила вывода: Ł36. Тp Тq - modus ponens: A, A B B - правило подстановки: A(р) A(р/B) Понятия доказательства и вывода – стандартны.

Определение остальных связок Ł3 соответствует классической логике, что для Лукасевича было определяющим: А В Df (А В) В А В Df ( А В) А В Df (А В) (В А)

Общие принципы построения многозначных логик I. Задаётся множество М возможных значений формул. Например, в PL 2 М = {0, 1}, а в Ł3 М = {0, ½, 1}. Дальнейшее обобщение достигается за счёт того, что в качестве элементов М берётся: 1) произвольное конечное число (k) значений в конечнозначных логиках. Например в Łk такие значения удобно обозначать посредством дробных чисел х таких, что 0 < x < 1, по принципу: М = {0, 1/k-1, 2/k-1, …, k-2/k-1, 1}. Так в Ł4 М = {0, 1/3, 2/3, 1}, а в Ł5 М = {0, 1/4, 2/4, 3/4, 1}. 2) все рациональные числа (представимые дробью n/m) в замкнутом интервале [0, 1] – в счётнозначной логике. 3) все действительные (рациональные и иррациональные) числа в замкнутом интервале [0, 1] – в континуальнозначной логике. II. Задаётся множество М* выделенных значений: М* М. Например, в PL 2 и в Ł3 М* = {1}, а в Ł*3 и в К*3 М = {½, 1}.

III. Определяется интерпретирующая функция φ, которая каждой переменной р сопоставляет значение из М: φ(р) М. Задаются правила приписывания значения произвольной формуле языка при интерпретации φ, где выражение метаязыка «|A|φ» читается как «значение формулы А при интерпретации φ» : |р|φ = φ(р), | А|φ = 1 - |А|φ, |А В|φ = min(|А|φ, |В|φ), |А В|φ = max(|А|φ, |В|φ), |А В|φ = min(1, 1 - |А|φ + |В|φ), |А В|φ = 1 – mod 1(|А|φ - |В|φ). 1 mod х – абсолютная величина (модуль) числа х.

В качестве примера установим в Ł4 значения молекулярных формул в случае, когда φ(р) = 1/3, а φ(q) = 2/3: | р|φ = 1 - 1/3 = 2/3, |р q|φ = min(1/3, 2/3) = 1/3, |А В|φ = max(1/3, 2/3) = 2/3, |А В|φ = min(1, 1 - 1/3 + 2/3) = min(1, 4/3) = 1, |А В|φ = 1 – mod(1/3 - 2/3) = 1 - mod(-1/3) = 1 - 1/3 = 2/3.

PL 2 (p (p q)) (p q) – «закон сокращения антецедентов» с 2 -х до 1 -го; Ł3 (p (p q)) (p q) и во всех Łn>3, но Ł3 (p (p (p q))) (p (p q)) – с 3 -х до 2 -х; Ł4 (p (p (p q))) (p q) и во всех Łn>4, но Ł4 (p (p q)))) (p (p (p q))) – с 4 -х до 3 -х и т. д. «Закон сокращения с m одинаковых антецедентов до m-1» имеет место в каждой Łk, где k m и не общезначим ни в одной Łk, k > m. В Ł ни одна формула указанного типа не общезначима. Однако, не всегда Łk+1 Łk. Соотношение более сложное (результат А. Линденбаума): Łk Łm, если и только если k-1 делится нацело на m-1. Например: Ł5 Ł3, но Ł4 Ł3.

Аксиоматизация Ł В системе Ł3 аксиома Ł34 заменяется на Ł 4. ((p q) q) ((q p) p). Классы законов счётнозначной и континуальнозначной логик Лукасевича совпадают, причём – Ł Łk, для любого k.