3 Аппроксимация_new.pptx
- Количество слайдов: 14

Актуальность. Цифровая информация. Преобразование. Пример: цифр. звук Тема 3. Аппроксимация (Википедия) Аппроксимация (приближение) — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми. Ср. МОДЕЛИРОВАНИЕ Мы рассмотрим аппроксимацию функций. Цели такой аппроксимации: 1. Заменить некоторую сложную функцию более простой, с которой удобнее работать; 2. Исходная функция может быть задана таблицей – результат эксперимента (статистических наблюдений); 3. Исходная функция может быть получена расчетами по сложным моделям (результаты расчетов – таблица). Пример. сложная функция ее график
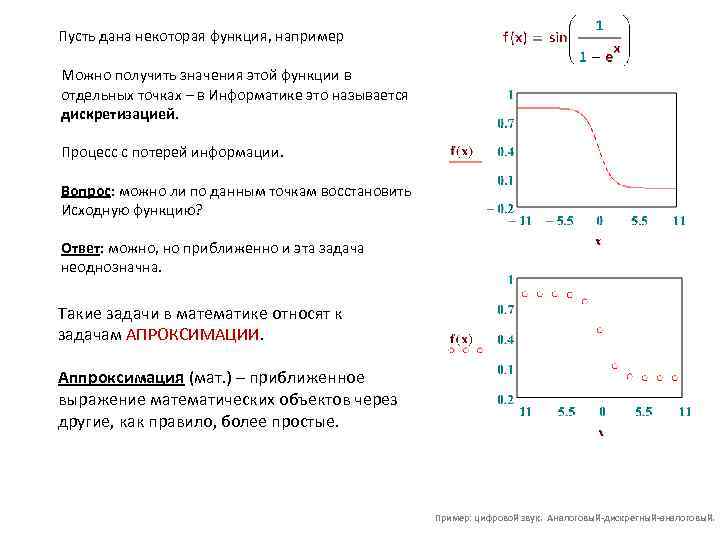
Пусть дана некоторая функция, например Можно получить значения этой функции в отдельных точках – в Информатике это называется дискретизацией. Процесс с потерей информации. Вопрос: можно ли по данным точкам восстановить Исходную функцию? Ответ: можно, но приближенно и эта задача неоднозначна. Такие задачи в математике относят к задачам АПРОКСИМАЦИИ. Аппроксимация (мат. ) – приближенное выражение математических объектов через другие, как правило, более простые. Пример: цифровой звук. Аналоговый-дискретный-аналоговый.
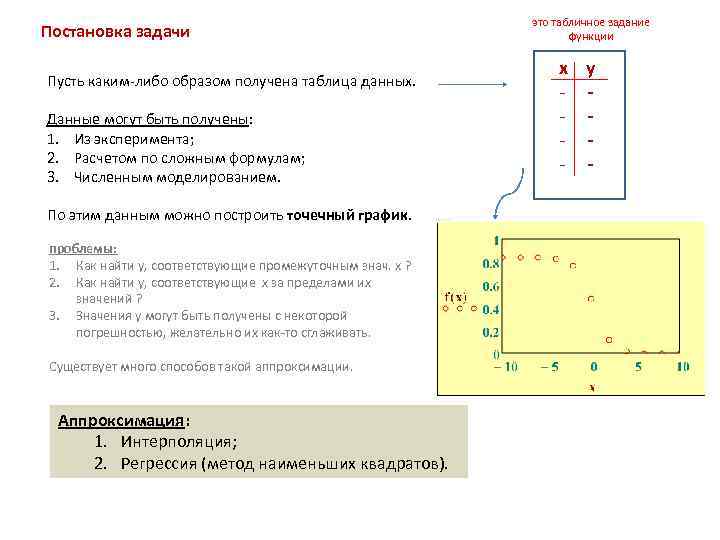
Постановка задачи Пусть каким-либо образом получена таблица данных. Данные могут быть получены: 1. Из эксперимента; 2. Расчетом по сложным формулам; 3. Численным моделированием. По этим данным можно построить точечный график. проблемы: 1. Как найти y, соответствующие промежуточным знач. x ? 2. Как найти y, соответствующие x за пределами их значений ? 3. Значения y могут быть получены с некоторой погрешностью, желательно их как-то сглаживать. Существует много способов такой аппроксимации. Аппроксимация: 1. Интерполяция; 2. Регрессия (метод наименьших квадратов). это табличное задание функции x - y -
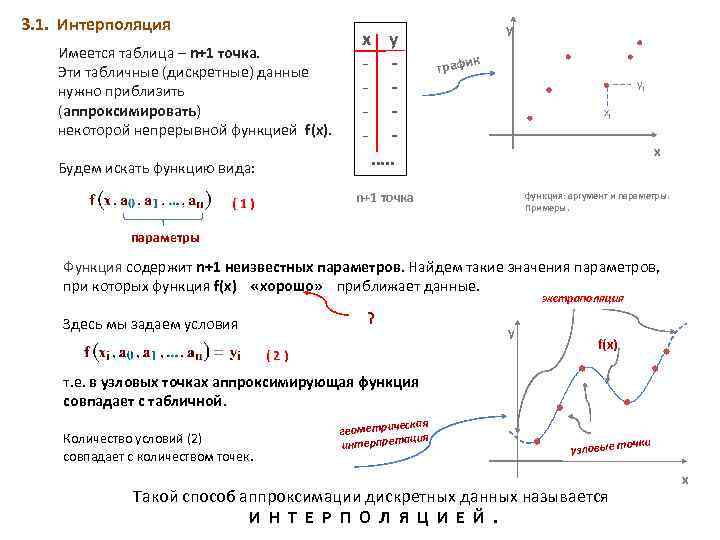
3. 1. Интерполяция Имеется таблица – n+1 точка. Эти табличные (дискретные) данные нужно приблизить (аппроксимировать) некоторой непрерывной функцией f(x). Будем искать функцию вида: x y - - …. . y к графи yi xi x n+1 точка (1) функция: аргумент и параметры. Примеры. параметры Функция содержит n+1 неизвестных параметров. Найдем такие значения параметров, при которых функция f(x) «хорошо» приближает данные. экстраполяция ? Здесь мы задаем условия (2) y f(x) т. е. в узловых точках аппроксимирующая функция совпадает с табличной. Количество условий (2) совпадает с количеством точек. ская геометриче ация интерпрет очки узловые т Такой способ аппроксимации дискретных данных называется И Н Т Е Р П О Л Я Ц И Е Й. x

линейная и нелинейная интерполяция набор из n линейно – независимых функций Если параметры ai входят в функцию (1) линейно, т. е. , то такая интерполяция называется линейной, в противном случае – нелинейной. (3) нелинейная интерполяция – сложный случай, здесь не рассматривается. интерполяционный многочлен Лагранжа На практике обычно использую частный случай (3), когда аппроксимирующая функция задается в виде многочлена – полинома n степени (4) n+1 неизвестных коэффициентов ai

(2) Для определения коэффициентов ai используем условия (2), которые приводят к системе n+1 линейных уравнений с n+1 неизвестным вида (5) Здесь неизвестны коэффициенты ai Определитель системы (5) -определитель Ван-дер-Монда. Он отличен от нуля (при условии различных xi), Следовательно система (5) имеет единственное решение. Это означает единственность интерполяционного многочлена (4) полином n степени один, но форм его записи много. Например: полином 2 степени.

Как найти коэффициенты ai ? методами линейной алгебры проблемы: много точек - большие матрицы, вычислительная погрешность, . . . другими методами Лагранж, Ньютон, . . . 18 век Идея: записать многочлен (4) в другой, более удобной для вычислений форме. Лагранж: предложил вместо (4) использовать многочлен вида (формула Лагранжа) полином n степени Частный случай 2 -х точек сокращенная форма -интерполяция прямой MC интерполяция (Demo)
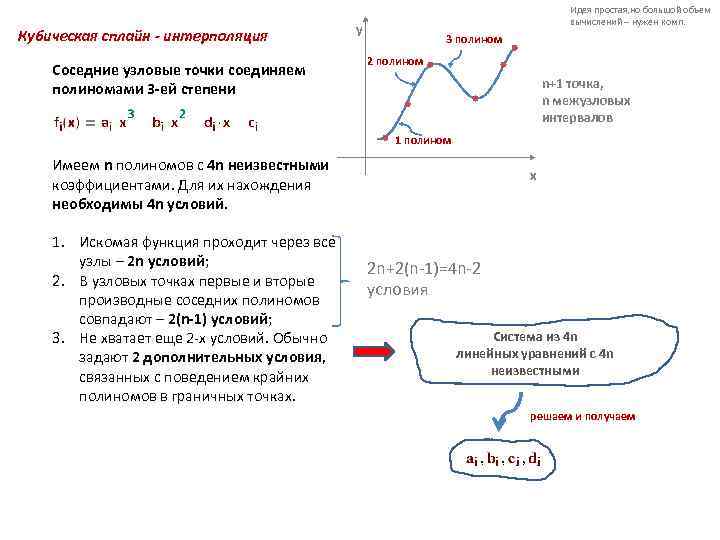
Кубическая сплайн - интерполяция Соседние узловые точки соединяем полиномами 3 -ей степени Идея простая, но большой объем вычислений – нужен комп. y 3 полином 2 полином n+1 точка, n межузловых интервалов 1 полином Имеем n полиномов с 4 n неизвестными коэффициентами. Для их нахождения необходимы 4 n условий. 1. Искомая функция проходит через все узлы – 2 n условий; 2. В узловых точках первые и вторые производные соседних полиномов совпадают – 2(n-1) условий; 3. Не хватает еще 2 -х условий. Обычно задают 2 дополнительных условия, связанных с поведением крайних полиномов в граничных точках. x 2 n+2(n-1)=4 n-2 условия Система из 4 n линейных уравнений с 4 n неизвестными решаем и получаем
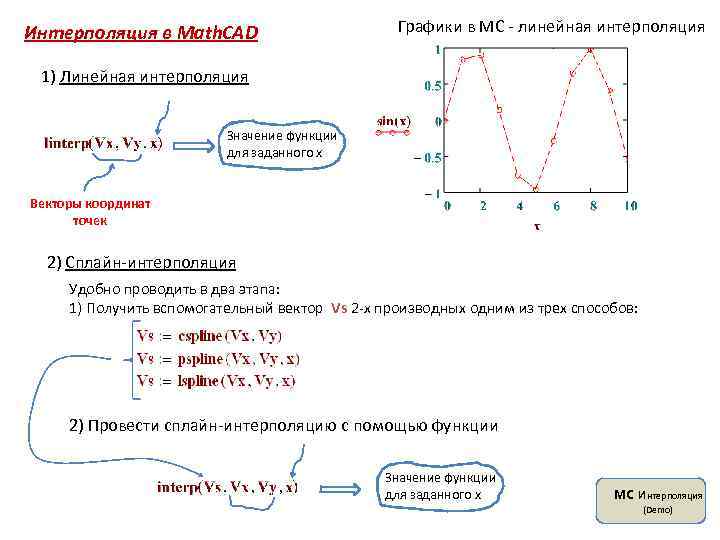
Интерполяция в Math. CAD Графики в MC - линейная интерполяция 1) Линейная интерполяция Значение функции для заданного x Векторы координат точек 2) Сплайн-интерполяция Удобно проводить в два этапа: 1) Получить вспомогательный вектор Vs 2 -х производных одним из трех способов: 2) Провести сплайн-интерполяцию с помощью функции Значение функции для заданного x MC интерполяция (Demo)

3. 2. Регрессия Метод наименьших квадратов Нужно точки аппроксимировать некоторой кривой, т. е. построить некоторую зависимость, которая наилучшим образом приближает данные: y ? x ГАУСС, КАРЛ ФРИДРИХ (1777– 1855), немецкий математик, астроном и физик. Пример: аргумент параметры В МНК вид функции f(x) задает пользователь, а параметры функции, которые обеспечивают наилучшее приближение, дает метод.
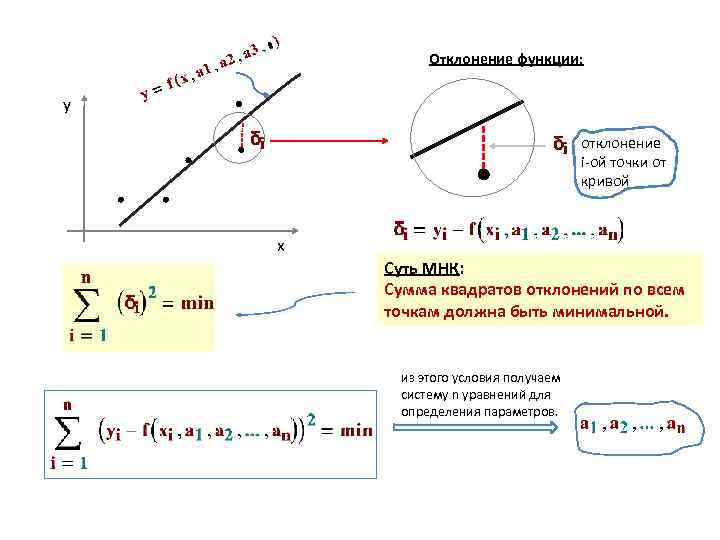
Отклонение функции: y отклонение i-ой точки от кривой x Суть МНК: Сумма квадратов отклонений по всем точкам должна быть минимальной. из этого условия получаем систему n уравнений для определения параметров.

Линейная и нелинейная регрессия Если параметры входят в аппроксимирующую функцию линейным образом, то полученная система уравнений будет линейной. Этот случай называется ЛИНЕЙНОЙ РЕГРЕССИЕЙ. Если нелинейно, то – НЕЛИНЕЙНАЯ РЕГРЕССИЯ. Примеры регрессии Линейная Нелинейная Линеаризация аппроксимирующей функции Иногда нелинейную регрессию можно свести к линейной путем линеаризации аппроксимирующей функции. Например, функция - н/л регрессия. Но ее можно линеаризовать. Для этого прологарифмируем ее и получим: Y A линейная регрессия

Регрессия в Math. CAD В МС есть следующие виды аппроксимации: • прямой; • полиномом n-степени: • общий случай линейной регрессии. Demo Math. CAD Электр. задание САМОСТОЯТЕЛЬНО ! (см. пособие)

3 Аппроксимация_new.pptx