Скачать презентацию Аксонометрические проекции Аксонометрической проекцией называется проекция полученная Скачать презентацию Аксонометрические проекции Аксонометрической проекцией называется проекция полученная

Lektsia_Axonometria.ppt

  • Количество слайдов: 23

Аксонометрические проекции Аксонометрические проекции

Аксонометрической проекцией называется проекция, полученная путем проецирования заданного предмета вместе с координатной системой параллельным Аксонометрической проекцией называется проекция, полученная путем проецирования заданного предмета вместе с координатной системой параллельным пучком лучей на некоторую плоскость α. Направление проецирования выбирают таким, чтобы оно не совпадало ни с одной из присоединенных координатных осей. Величины изображений ребер параллелепипеда на плоскости α определяются коэффициентами искажения kx, ky и kz. Проекции присоединенных координатных осей на плоскость α называют аксонометрическими осями.

ГОСТ 2. 317– 69 « Аксонометрические проекции» устанавливает аксонометрические проекции, применяемые в чертежах всех ГОСТ 2. 317– 69 « Аксонометрические проекции» устанавливает аксонометрические проекции, применяемые в чертежах всех отраслей промышленности и строительства. Аксонометрические проекции бывают: - изометрические, если коэффициенты искажения по всем трем осям равны между собой kx=ky=kz - диметрические, если коэффициенты искажения по двум любым осям равны между собой kx= kz ≠ky - триметрические, если все три коэффициента искажения различны kx≠ky≠kz.

В зависимости от направления проецирующих лучей аксонометрические проекции делятся на прямоугольные и косоугольные. Прямоугольная В зависимости от направления проецирующих лучей аксонометрические проекции делятся на прямоугольные и косоугольные. Прямоугольная аксонометрическая проекция - проецирующие лучи перпендикулярны аксонометрической плоскости проекций. Косоугольная аксонометрическая проекция проецирующие лучи направлены под углом к аксонометрической плоскости проекций

Прямоугольные аксонометрические проекции 1. Изометрическая 2. Диметрическая Прямоугольные аксонометрические проекции 1. Изометрическая 2. Диметрическая

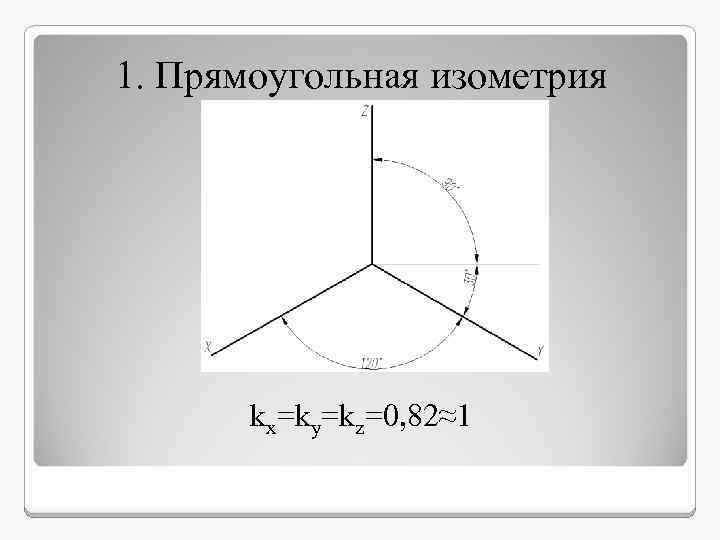1. Прямоугольная изометрия kx=ky=kz=0, 82≈1 1. Прямоугольная изометрия kx=ky=kz=0, 82≈1

В прямоугольной изометрии окружности изображаются в виде эллипсов. Большая ось эллипса перпендикулярна отсутствующей В прямоугольной изометрии окружности изображаются в виде эллипсов. Большая ось эллипса перпендикулярна отсутствующей в плоскости оси, а малая ей параллельна Б. О. Э. = 1, 22 d М. О. Э. =0, 71 d

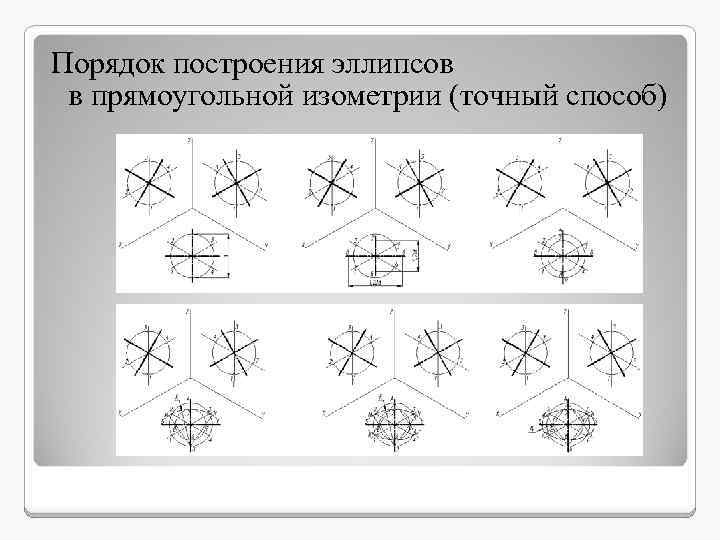Порядок построения эллипсов в прямоугольной изометрии (точный способ) Порядок построения эллипсов в прямоугольной изометрии (точный способ)

Порядок построения эллипсов в прямоугольной изометрии (приближённый способ) 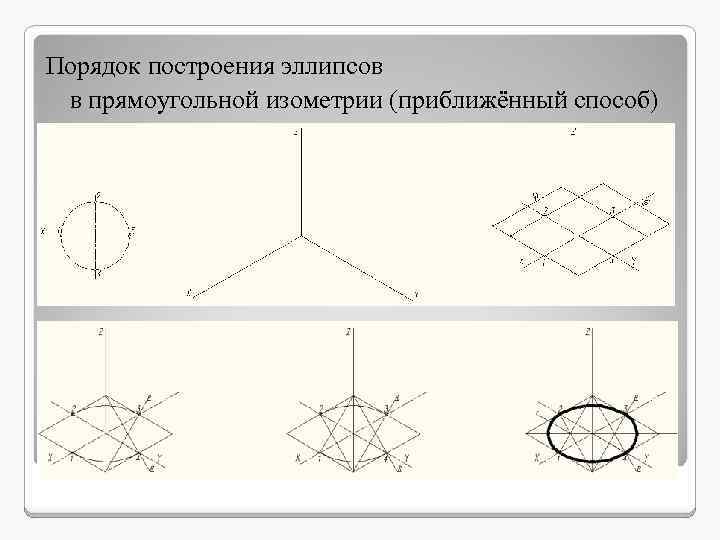Порядок построения эллипсов в прямоугольной изометрии (приближённый способ)

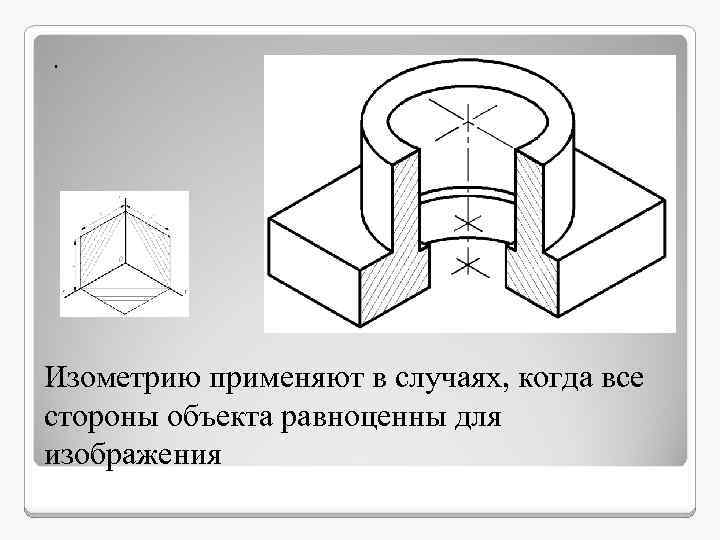. Изометрию применяют в случаях, когда все стороны объекта равноценны для изображения . Изометрию применяют в случаях, когда все стороны объекта равноценны для изображения

2. Прямоугольная диметрия ky=0, 47≈0, 5, kx=kz=0, 94≈1. 2. Прямоугольная диметрия ky=0, 47≈0, 5, kx=kz=0, 94≈1.

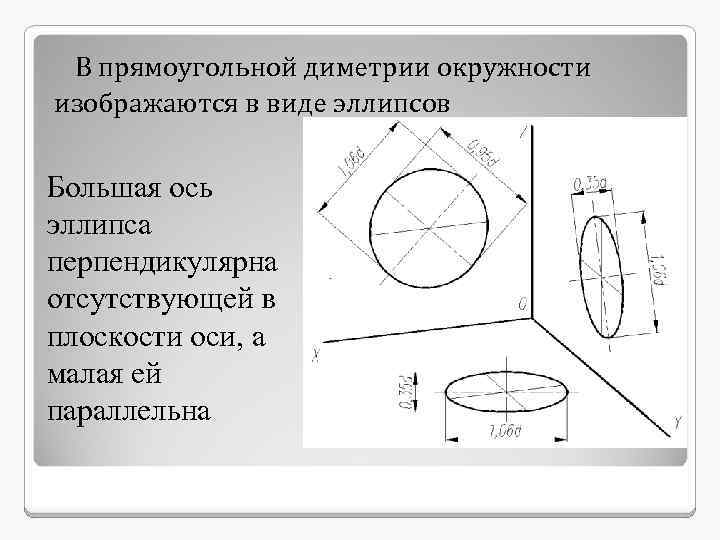В прямоугольной диметрии окружности изображаются в виде эллипсов Большая ось эллипса перпендикулярна отсутствующей в В прямоугольной диметрии окружности изображаются в виде эллипсов Большая ось эллипса перпендикулярна отсутствующей в плоскости оси, а малая ей параллельна

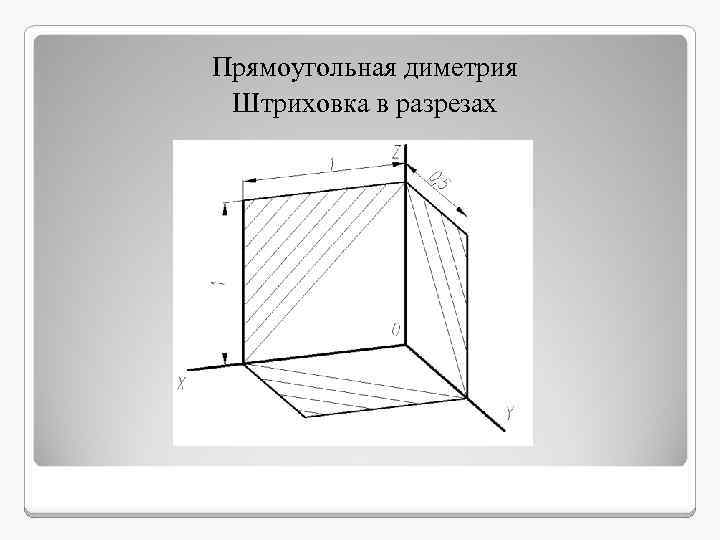Прямоугольная диметрия Штриховка в разрезах Прямоугольная диметрия Штриховка в разрезах

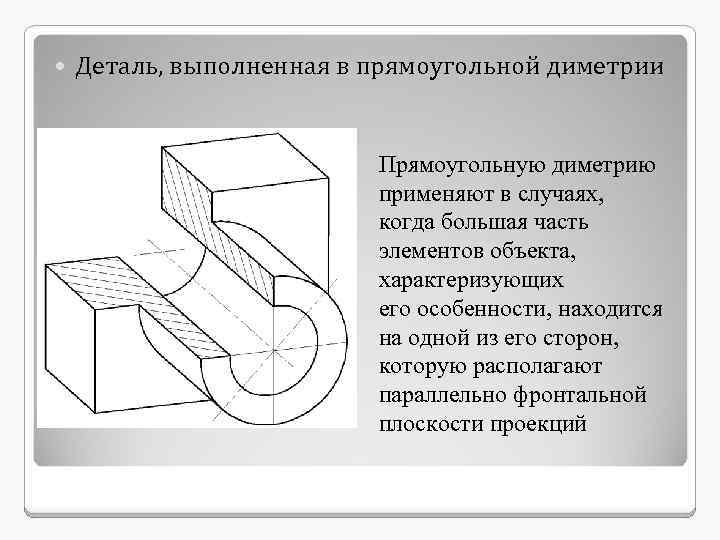Деталь, выполненная в прямоугольной диметрии Прямоугольную диметрию применяют в случаях, когда большая часть Деталь, выполненная в прямоугольной диметрии Прямоугольную диметрию применяют в случаях, когда большая часть элементов объекта, характеризующих его особенности, находится на одной из его сторон, которую располагают параллельно фронтальной плоскости проекций

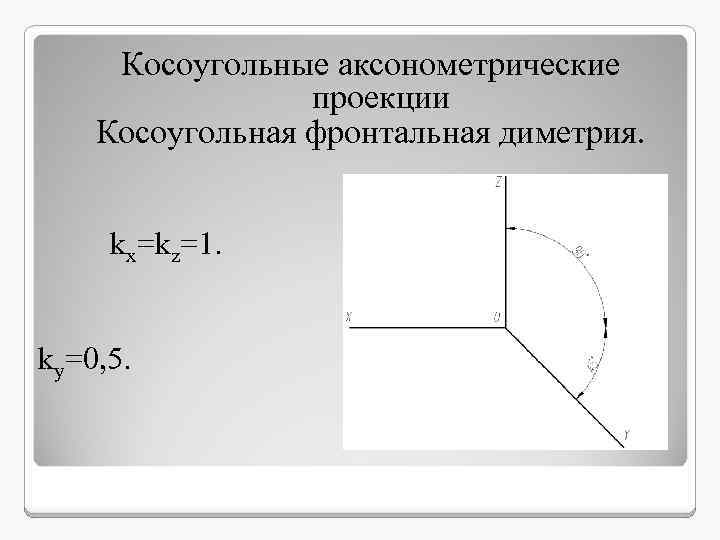Косоугольные аксонометрические проекции Косоугольная фронтальная диметрия. kx=kz=1. ky=0, 5. Косоугольные аксонометрические проекции Косоугольная фронтальная диметрия. kx=kz=1. ky=0, 5.

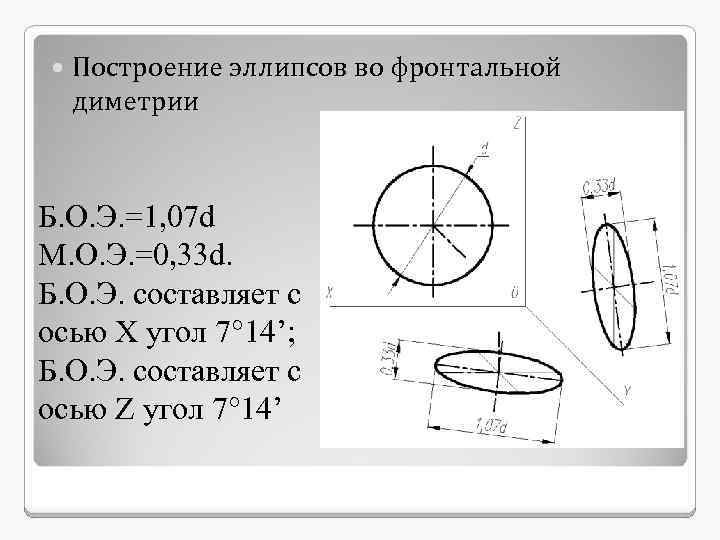Построение эллипсов во фронтальной диметрии Б. О. Э. =1, 07 d М. О. Построение эллипсов во фронтальной диметрии Б. О. Э. =1, 07 d М. О. Э. =0, 33 d. Б. О. Э. составляет с осью X угол 7° 14’; Б. О. Э. составляет с осью Z угол 7° 14’

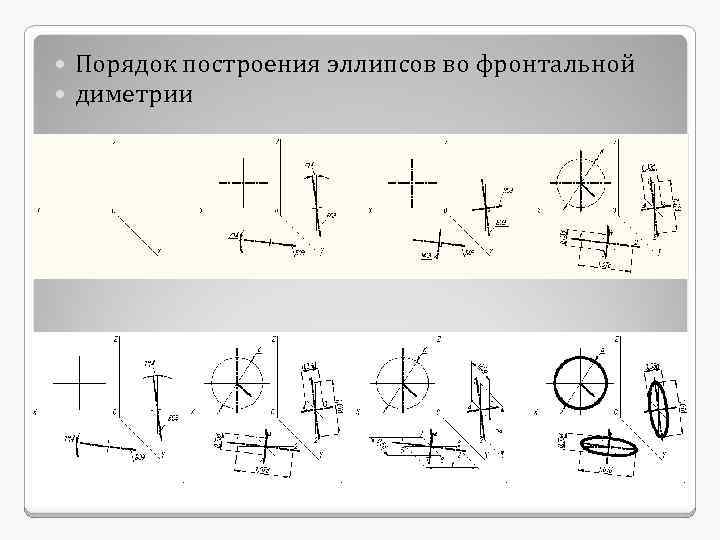Порядок построения эллипсов во фронтальной диметрии Порядок построения эллипсов во фронтальной диметрии

Порядок построения детали во фронтальной диметрии 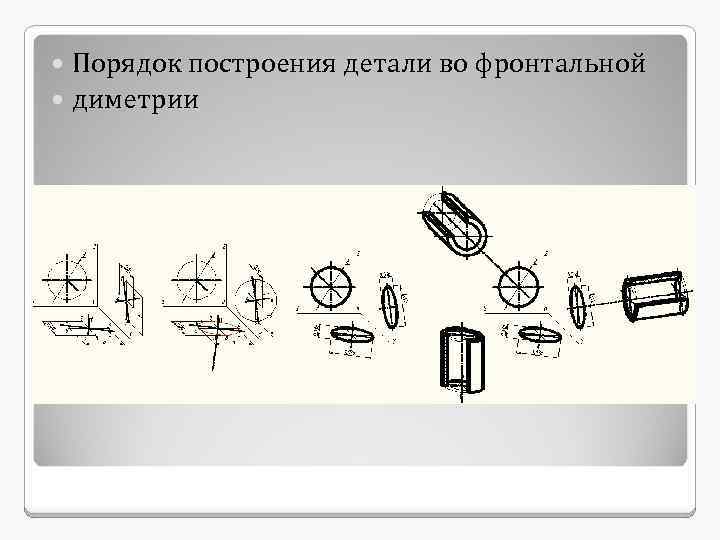Порядок построения детали во фронтальной диметрии

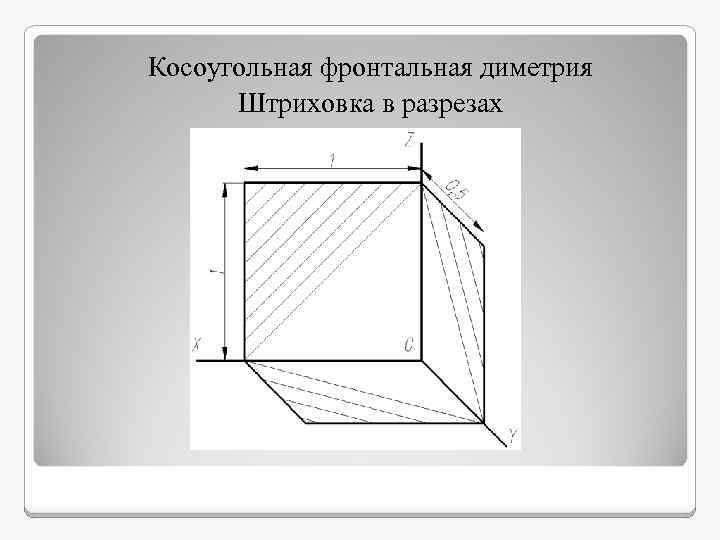Косоугольная фронтальная диметрия Штриховка в разрезах Косоугольная фронтальная диметрия Штриховка в разрезах

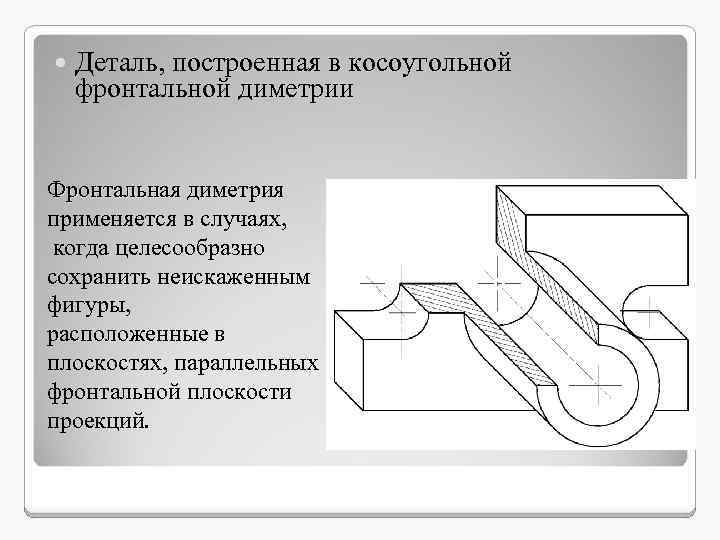Деталь, построенная в косоугольной фронтальной диметрии ◦ Фронтальная диметрия Фронтальная применяется в случаях, Деталь, построенная в косоугольной фронтальной диметрии ◦ Фронтальная диметрия Фронтальная применяется в случаях, когда целесообразно сохранить неискаженным фигуры, расположенные в плоскостях, параллельных фронтальной плоскости проекций.

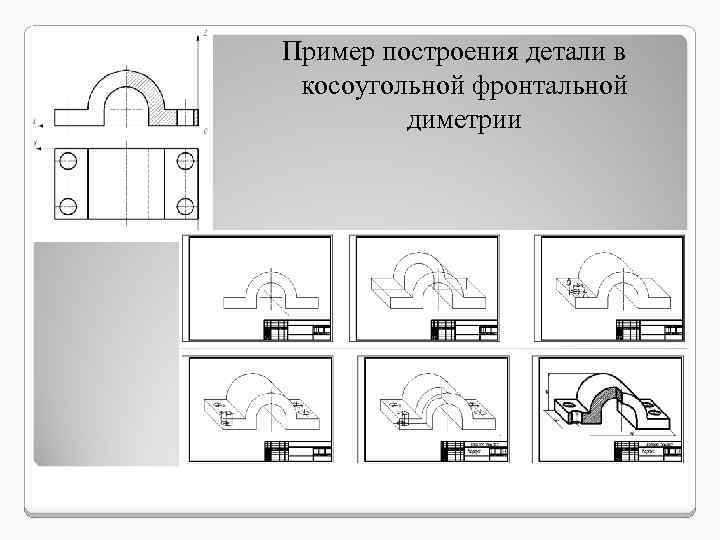Пример построения детали в косоугольной фронтальной диметрии Пример построения детали в косоугольной фронтальной диметрии

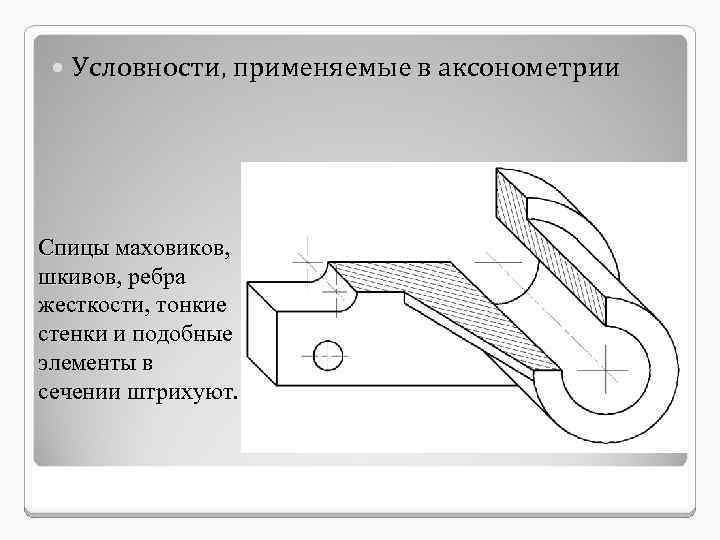Условности, применяемые в аксонометрии Спицы маховиков, шкивов, ребра шкивов, жесткости, тонкие стенки и Условности, применяемые в аксонометрии Спицы маховиков, шкивов, ребра шкивов, жесткости, тонкие стенки и подобные элементы в сечении штрихуют.

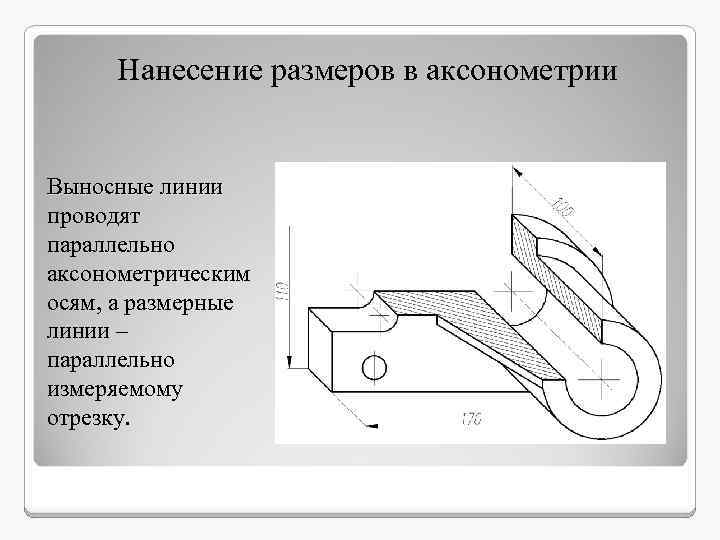Нанесение размеров в аксонометрии Выносные линии проводят параллельно аксонометрическим осям, а размерные линии – Нанесение размеров в аксонометрии Выносные линии проводят параллельно аксонометрическим осям, а размерные линии – параллельно измеряемому отрезку.