Аксиомы стереометрии Урок 3 -4

Аксиомы стереометрии Урок 3 -4

• • • • Повторение лекции что изучает стереометрия? назовите основные понятия стереометрии как обозначается точка, прямая, плоскость? как записать с помощью математических знаков, что точка не принадлежит прямой? как записать, что прямая пересекает плоскость? что такое аксиома? чем отличается теорема от аксиомы? Сформулируйте аксиомы стереометрии Сформулируйте аксиому , дающую представление о способе задания плоскости Сформулируйте аксиому, дающую представление о взаимном расположении прямой и плоскости Сколько плоскостей можно провести через прямую а? Сформулируйте аксиому , дающую представление о. взаимном расположении плоскостей Назовите способы задания плоскости Докажите, что через две параллельные пряме можно провести плоскость Как прямая может располагаться относительно плоскости?

Дополнение теоретического материала Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися. Прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаються. • Всегда ли параллельные пряме лежат в одной плоскости? • В параллелепипеде укажите параллельные и скрещивающиеся прямые

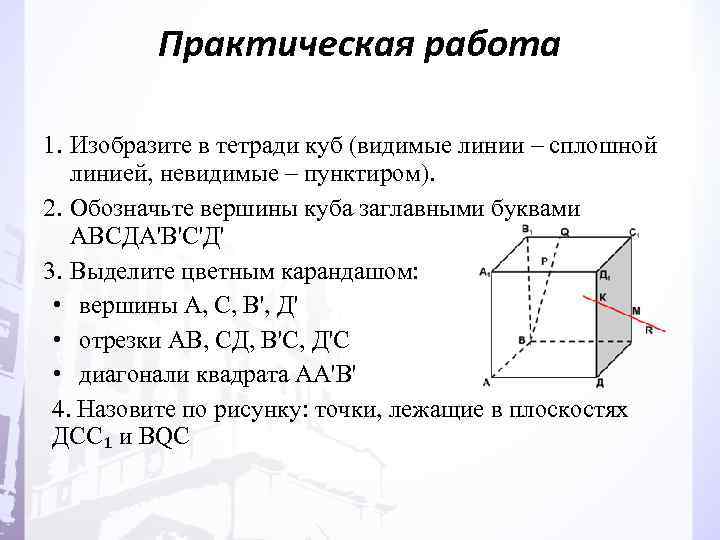Практическая работа 1. Изобразите в тетради куб (видимые линии – сплошной линией, невидимые – пунктиром). 2. Обозначьте вершины куба заглавными буквами АВСДА'В'С'Д' 3. Выделите цветным карандашом: • вершины А, С, В', Д' • отрезки АВ, СД, В'С, Д'С • диагонали квадрата АА'В' 4. Назовите по рисунку: точки, лежащие в плоскостях ДСС₁ и ВQС

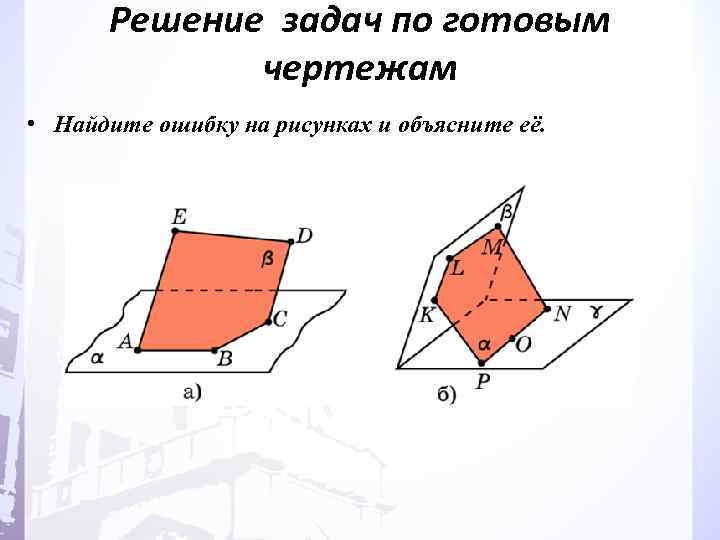Решение задач по готовым чертежам • Найдите ошибку на рисунках и объясните её.

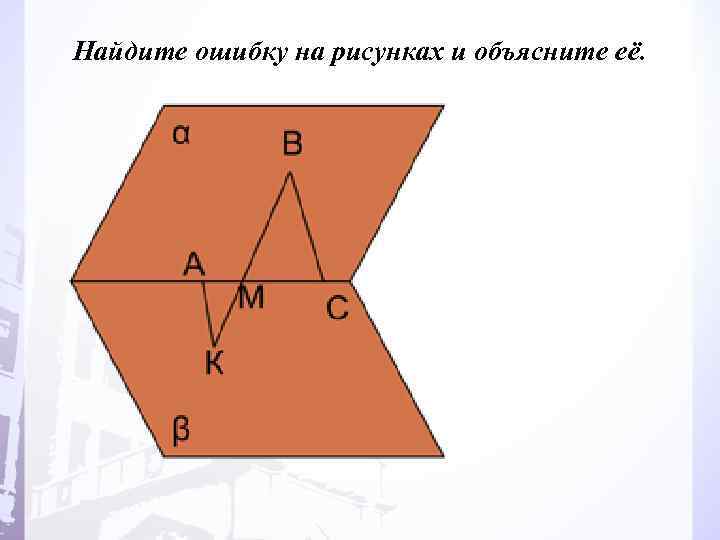Найдите ошибку на рисунках и объясните её.

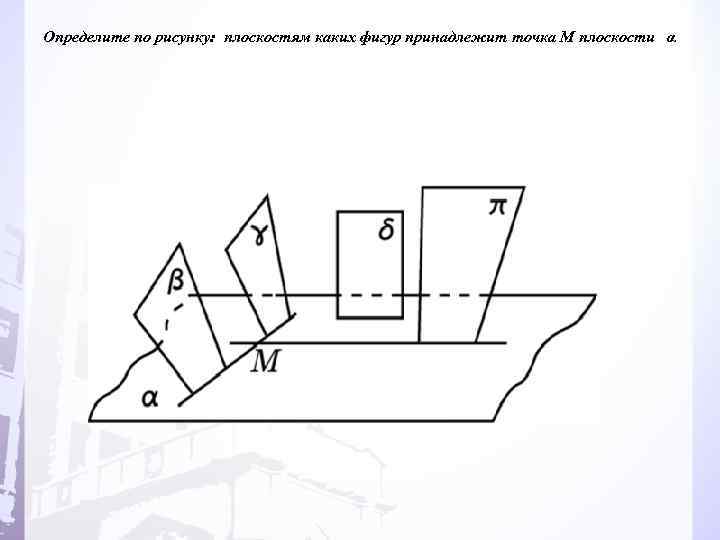Определите по рисунку: плоскостям каких фигур принадлежит точка M плоскости α

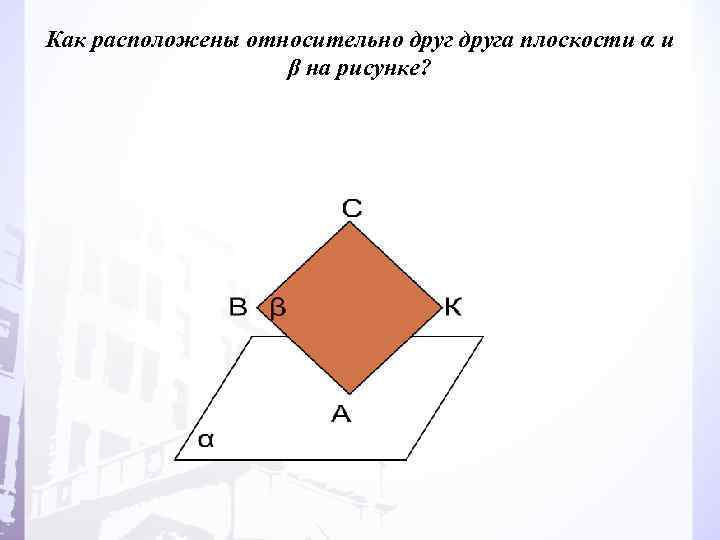Как расположены относительно друга плоскости α и β на рисунке?

Тест № 1 1. Выберите верное суждение. • А) Как бы ни было, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей. • Б) Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей. • В) Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости. • Г) Какова бы ни была плоскость, существуют точки в пространстве, не принадлежащие ей.

2. Выберите верное суждение • А) Если плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. • Б) Если две различные плоскости имеют общую точку, то они пересекаются по прямой. • В) Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. • 3. Выберите верное суждение • А) Через две прямые можно провести плоскость и притом только одну. • Б) Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну. • В) Если прямые имеют общую точку, то через них можно провести плоскость.

Ключ: 1 – Б) 2 – В) 3 – Б)

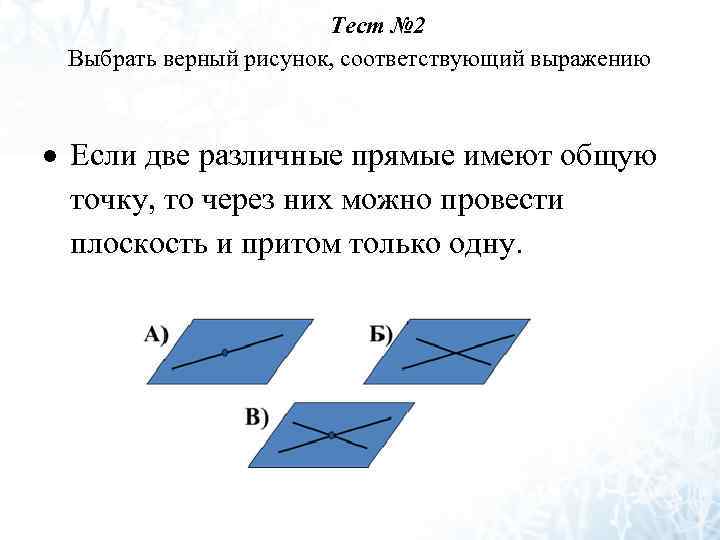Тест № 2 Выбрать верный рисунок, соответствующий выражению Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.

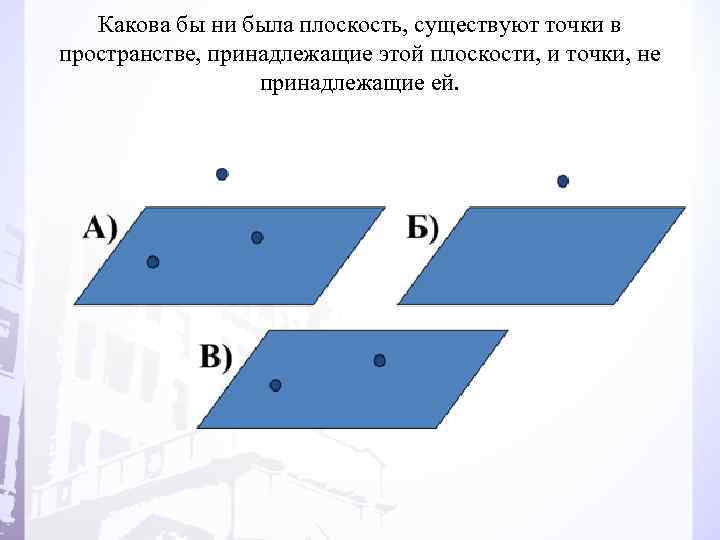Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.

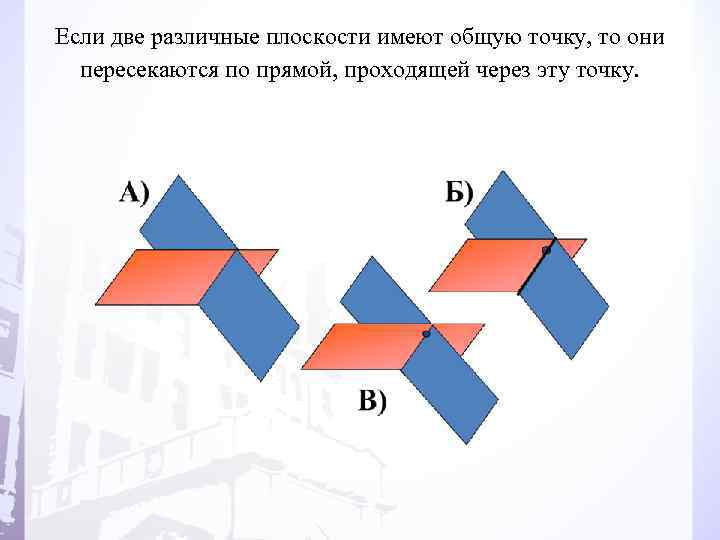Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

• Ключ: 1) – В 2) – А 3) – Б

Домашнее задание • Дан куб АВСDA 1 B 1 C 1 D 1. Точка М лежит на ребре DD₁. Точка N лежит на ребре CC 1. Точка K лежит на ребре BB 1. Найти точку пересечения прямых MN и DС.