Аксиомы 10 класс, 2009 год Аксиомы

Аксиомы 10 класс, 2009 год

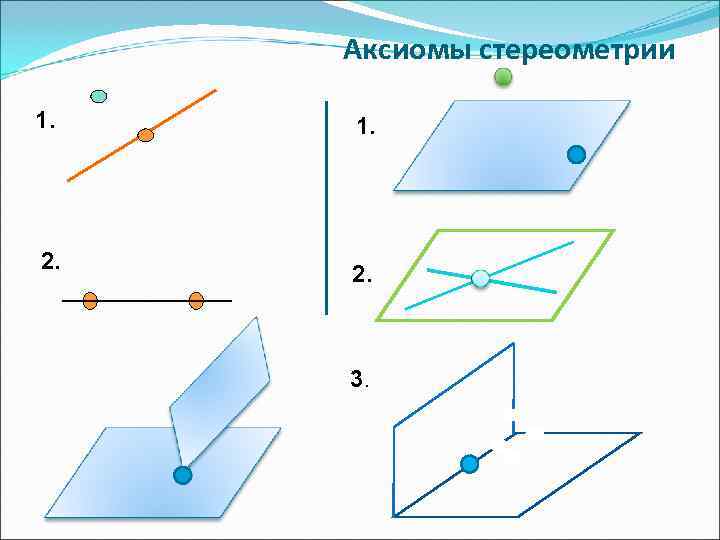Аксиомы стереометрии 1. 2. 3.

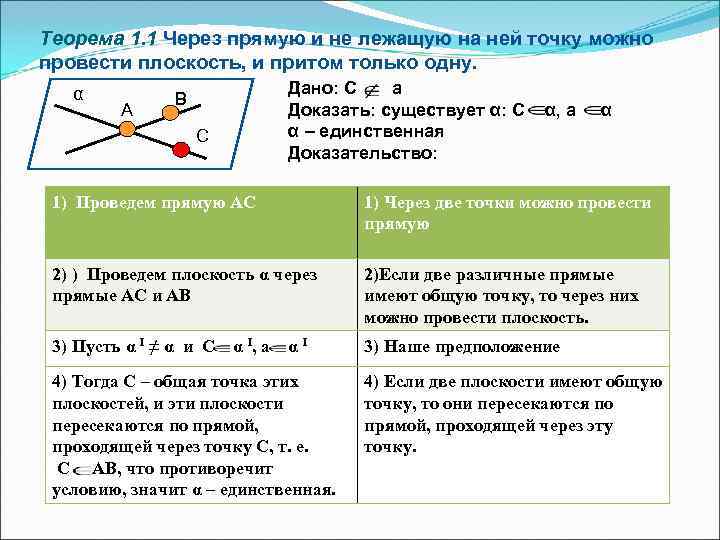Теорема 1. 1 Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. Дано: С а α В А Доказать: существует α: С α, а α С α – единственная Доказательство: 1) Проведем прямую АС 1) Через две точки можно провести прямую 2) ) Проведем плоскость α через 2)Если две различные прямые АС и АВ имеют общую точку, то через них можно провести плоскость. 3) Пусть α I ≠ α и С α I, а αI 3) Наше предположение 4) Тогда С – общая точка этих 4) Если две плоскости имеют общую плоскостей, и эти плоскости точку, то они пересекаются по прямой, проходящей через эту проходящей через точку С, т. е. точку. С АВ, что противоречит условию, значит α – единственная.

Теорема 1. 2. Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости. Дано: В, С а, В, С α А Доказать: а α С α Доказательство: α 2 1 В 1) Возьмем точку А а 1) Через две точки можно провести прямую 2) Проведем плоскость α 2 через 2) Через прямую и не лежащую на прямую а и точку А ней точку, можно провести плоскость, и притом только одну. 3) Если α 2 = α 1 , а α 1 3) Следует из пункта 2. 4) Если α 2 ≠ α 1 , то α 2 пересекает α 1 4) Если две плоскости имеют общую по прямой а I, которая содержит точку, то они пересекаются по прямой, две точки прямой а, а значит проходящей через эту точку. совпадает с ней. Следовательно , а α 1