Агент — ориентированные модели. Основные понятия

























Лекция 14 - Агентное моделирование.ppt
- Количество слайдов: 28
 Агент - ориентированные модели. Основные понятия Лекция 14
Агент - ориентированные модели. Основные понятия Лекция 14
 Агент-ориентированные модели ( agent based models, АОМ) относятся к классу моделей, основанных на индивидуальном поведении агентов. Основная идея - построение вычислительного инструмента, представляющего собой совокупность агентов с определенным набором свойств и позволяющего проводить имитацию реальных явлений. Сев. НТУ, кафедра Ки. ВТ, курс 2 "Моделирование", 2013, Лекция 14
Агент-ориентированные модели ( agent based models, АОМ) относятся к классу моделей, основанных на индивидуальном поведении агентов. Основная идея - построение вычислительного инструмента, представляющего собой совокупность агентов с определенным набором свойств и позволяющего проводить имитацию реальных явлений. Сев. НТУ, кафедра Ки. ВТ, курс 2 "Моделирование", 2013, Лекция 14
 Особенности агентных моделей (АМ) Агентные модели существенно децентрализованы. В АМ нет такого места, где централизованно определялось бы поведение (динамика) системы вцелом. Вместо этого, аналитик определяет поведение на индивидуальном уровне , а глобальное поведение возникает как результат деятельности многих агентов, каждый из которых следует своим собственным правилам, живёт в общей среде и взаимодействует со средой и с другими агентами. Поэтому АМ называют ещё моделированием снизу вверх. Сев. НТУ, кафедра Ки. ВТ, курс 3 "Моделирование", 2013, Лекция 14
Особенности агентных моделей (АМ) Агентные модели существенно децентрализованы. В АМ нет такого места, где централизованно определялось бы поведение (динамика) системы вцелом. Вместо этого, аналитик определяет поведение на индивидуальном уровне , а глобальное поведение возникает как результат деятельности многих агентов, каждый из которых следует своим собственным правилам, живёт в общей среде и взаимодействует со средой и с другими агентами. Поэтому АМ называют ещё моделированием снизу вверх. Сев. НТУ, кафедра Ки. ВТ, курс 3 "Моделирование", 2013, Лекция 14
 Свойства АОМ 1. Автономия. 2. Неоднородность. 3. Ограниченная интеллектуальность агентов. 4. Расположение в пространстве. Сев. НТУ, кафедра Ки. ВТ, курс 4 "Моделирование", 2013, Лекция 14
Свойства АОМ 1. Автономия. 2. Неоднородность. 3. Ограниченная интеллектуальность агентов. 4. Расположение в пространстве. Сев. НТУ, кафедра Ки. ВТ, курс 4 "Моделирование", 2013, Лекция 14
 Свойства АОМ Автономия. Агенты действуют независимо друг от друга и при этом предполагается, что в моделях нет единой регулирующей структуры, которая контролировала бы поведение каждого агента в отдельности. При этом взаимодействие микро- и макро- уровней в моделях осуществляется следующим образом: на макроуровне задается общий для всех агентов набор правил; совокупность действий агентов микроуровня может оказывать влияние на параметры макроуровня. Сев. НТУ, кафедра Ки. ВТ, курс 5 "Моделирование", 2013, Лекция 14
Свойства АОМ Автономия. Агенты действуют независимо друг от друга и при этом предполагается, что в моделях нет единой регулирующей структуры, которая контролировала бы поведение каждого агента в отдельности. При этом взаимодействие микро- и макро- уровней в моделях осуществляется следующим образом: на макроуровне задается общий для всех агентов набор правил; совокупность действий агентов микроуровня может оказывать влияние на параметры макроуровня. Сев. НТУ, кафедра Ки. ВТ, курс 5 "Моделирование", 2013, Лекция 14
 Свойства АОМ Неоднородность. Агенты чем-то различаются друг от друга, что принципиально отличает АОМ от широко распространенных моделей с агентом-представителем, причем различия между агентами могут проявляться по многим параметрам (в случае агентов, отображающих людей, это могут быть параметры уровня здоровья, дохода, культурного уровня, правил принятия решений и т. д. ). Сев. НТУ, кафедра Ки. ВТ, курс 6 "Моделирование", 2013, Лекция 14
Свойства АОМ Неоднородность. Агенты чем-то различаются друг от друга, что принципиально отличает АОМ от широко распространенных моделей с агентом-представителем, причем различия между агентами могут проявляться по многим параметрам (в случае агентов, отображающих людей, это могут быть параметры уровня здоровья, дохода, культурного уровня, правил принятия решений и т. д. ). Сев. НТУ, кафедра Ки. ВТ, курс 6 "Моделирование", 2013, Лекция 14
 Свойства АОМ Ограниченная интеллектуальность агентов (или ограниченная рациональность). Агенты модели не могут познать (выполнить) нечто большее, выходящее за рамки макросреды модели. Расположение в пространстве. Некоторая «среда обитания» , которая может быть представлена как в виде решетки, так и в виде гораздо более сложной структуры. (Это свойство не обязательно). Сев. НТУ, кафедра Ки. ВТ, курс 7 "Моделирование", 2013, Лекция 14
Свойства АОМ Ограниченная интеллектуальность агентов (или ограниченная рациональность). Агенты модели не могут познать (выполнить) нечто большее, выходящее за рамки макросреды модели. Расположение в пространстве. Некоторая «среда обитания» , которая может быть представлена как в виде решетки, так и в виде гораздо более сложной структуры. (Это свойство не обязательно). Сев. НТУ, кафедра Ки. ВТ, курс 7 "Моделирование", 2013, Лекция 14
 Агент в АОМ - автономная сущность, как правило имеющая графическое представление, с определенной целью функционирования и возможностью обучения в процессе существования до определенного уровня, определяемого разработчиками соответствующей модели. Сев. НТУ, кафедра Ки. ВТ, курс 8 "Моделирование", 2013, Лекция 14
Агент в АОМ - автономная сущность, как правило имеющая графическое представление, с определенной целью функционирования и возможностью обучения в процессе существования до определенного уровня, определяемого разработчиками соответствующей модели. Сев. НТУ, кафедра Ки. ВТ, курс 8 "Моделирование", 2013, Лекция 14
 Примеры агентов 1) Люди (или другие живые организмы), роботы, автомобили и другие подвижные объекты; 2) Недвижимые объекты; 3) Совокупности однотипных объектов. Сев. НТУ, кафедра Ки. ВТ, курс 9 "Моделирование", 2013, Лекция 14
Примеры агентов 1) Люди (или другие живые организмы), роботы, автомобили и другие подвижные объекты; 2) Недвижимые объекты; 3) Совокупности однотипных объектов. Сев. НТУ, кафедра Ки. ВТ, курс 9 "Моделирование", 2013, Лекция 14
 Примеры применения АОМ • оптимизация сети поставщиков и планирование перевозок; • планирование развития производства; • прогнозирование спроса на продукцию и объема продаж; • оптимизация численности персонала; • прогнозирование развития социально- экономических систем (городов, регионов); • моделирование миграционных процессов; • имитация и оптимизация пешеходного движения; • моделирование транспортных систем; Сев. НТУ, кафедра Ки. ВТ, курс 10 "Моделирование", 2013, Лекция 14
Примеры применения АОМ • оптимизация сети поставщиков и планирование перевозок; • планирование развития производства; • прогнозирование спроса на продукцию и объема продаж; • оптимизация численности персонала; • прогнозирование развития социально- экономических систем (городов, регионов); • моделирование миграционных процессов; • имитация и оптимизация пешеходного движения; • моделирование транспортных систем; Сев. НТУ, кафедра Ки. ВТ, курс 10 "Моделирование", 2013, Лекция 14
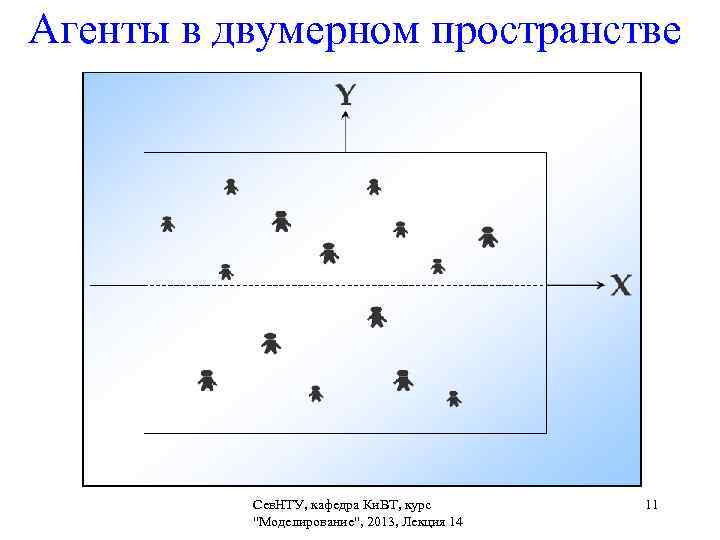
 Агенты в двумерном пространстве Сев. НТУ, кафедра Ки. ВТ, курс 11 "Моделирование", 2013, Лекция 14
Агенты в двумерном пространстве Сев. НТУ, кафедра Ки. ВТ, курс 11 "Моделирование", 2013, Лекция 14
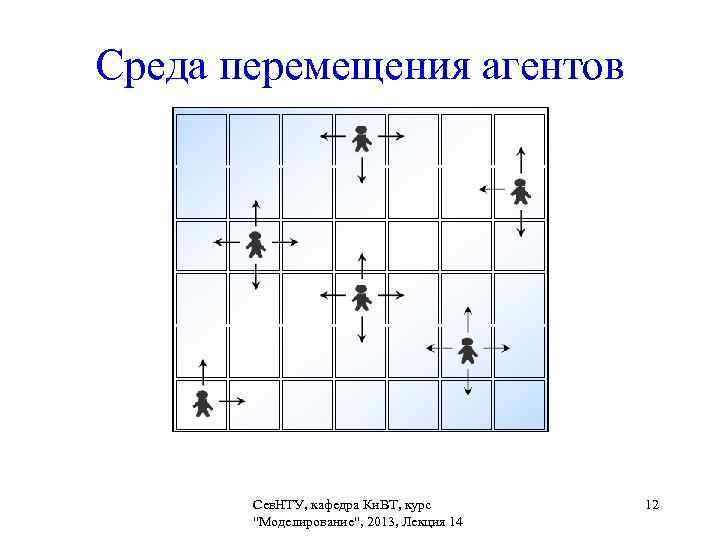
 Среда перемещения агентов Сев. НТУ, кафедра Ки. ВТ, курс 12 "Моделирование", 2013, Лекция 14
Среда перемещения агентов Сев. НТУ, кафедра Ки. ВТ, курс 12 "Моделирование", 2013, Лекция 14
 Общая модель взаимодействия интеллектуальных агентов MI =
Общая модель взаимодействия интеллектуальных агентов MI =
 Преимущества АОМ - АОМ позволяют смоделировать систему максимально приближенную к реальности. - Степень детализации АОМ ограничивается только возможностями компьютеров. - В ряде АОМ передвижение агентов задается без использования сложных формул, с помощью заранее определенных маршрутов и простых правил, с одной стороны имитирующих адаптивное мышление в процессе принятия решений, а с другой –позволяющих получить не очевидные результаты на уровне агрегированных параметров. Сев. НТУ, кафедра Ки. ВТ, курс 14 "Моделирование", 2013, Лекция 14
Преимущества АОМ - АОМ позволяют смоделировать систему максимально приближенную к реальности. - Степень детализации АОМ ограничивается только возможностями компьютеров. - В ряде АОМ передвижение агентов задается без использования сложных формул, с помощью заранее определенных маршрутов и простых правил, с одной стороны имитирующих адаптивное мышление в процессе принятия решений, а с другой –позволяющих получить не очевидные результаты на уровне агрегированных параметров. Сев. НТУ, кафедра Ки. ВТ, курс 14 "Моделирование", 2013, Лекция 14
 ПРИМЕРЫ АОМ Сев. НТУ, кафедра Ки. ВТ, курс 15 "Моделирование", 2013, Лекция 14
ПРИМЕРЫ АОМ Сев. НТУ, кафедра Ки. ВТ, курс 15 "Моделирование", 2013, Лекция 14
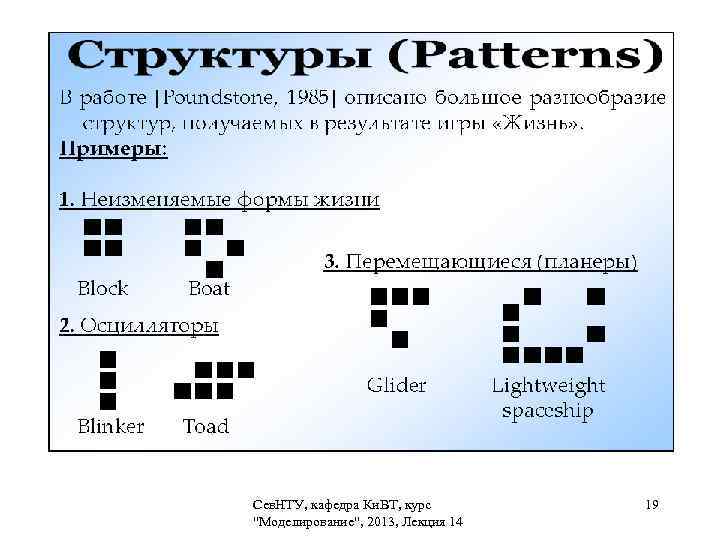
 Игра «Жизнь» Наиболее известная реализация взаимодействия клеточных автоматов, предложена Джоном Конвеем ( John Conway) в 1970 году. Место действия игры — вселенная — размеченная на клетки поверхность. Каждая клетка может находиться в двух состояниях: живая или мертвая. Клетка имеет восемь соседей. Распределение живых клеток в начале игры называется первым поколением. Сев. НТУ, кафедра Ки. ВТ, курс 16 "Моделирование", 2013, Лекция 14
Игра «Жизнь» Наиболее известная реализация взаимодействия клеточных автоматов, предложена Джоном Конвеем ( John Conway) в 1970 году. Место действия игры — вселенная — размеченная на клетки поверхность. Каждая клетка может находиться в двух состояниях: живая или мертвая. Клетка имеет восемь соседей. Распределение живых клеток в начале игры называется первым поколением. Сев. НТУ, кафедра Ки. ВТ, курс 16 "Моделирование", 2013, Лекция 14
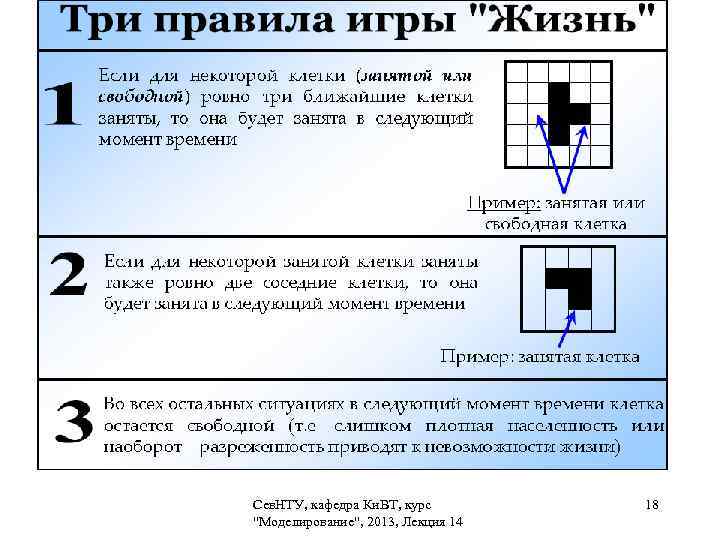
 Игра «Жизнь» Каждое следующее поколение рассчитывается на основе предыдущего по следующим правилам: — пустая (мертвая) клетка рядом с тремя живыми клетками-соседями оживает; — если у живой клетки есть две или три живые соседки, то эта клетка продолжает жить; в противном случае (если соседей меньше двух или больше трех) клетка умирает (от «одиночества» или от «перенаселенности» ). Состояние конечного автомата в момент t + 1 является функцией от его собственного состояния и состояния его соседей в момент времени t. Сев. НТУ, кафедра Ки. ВТ, курс 17 "Моделирование", 2013, Лекция 14
Игра «Жизнь» Каждое следующее поколение рассчитывается на основе предыдущего по следующим правилам: — пустая (мертвая) клетка рядом с тремя живыми клетками-соседями оживает; — если у живой клетки есть две или три живые соседки, то эта клетка продолжает жить; в противном случае (если соседей меньше двух или больше трех) клетка умирает (от «одиночества» или от «перенаселенности» ). Состояние конечного автомата в момент t + 1 является функцией от его собственного состояния и состояния его соседей в момент времени t. Сев. НТУ, кафедра Ки. ВТ, курс 17 "Моделирование", 2013, Лекция 14
 Сев. НТУ, кафедра Ки. ВТ, курс 18 "Моделирование", 2013, Лекция 14
Сев. НТУ, кафедра Ки. ВТ, курс 18 "Моделирование", 2013, Лекция 14
 Сев. НТУ, кафедра Ки. ВТ, курс 19 "Моделирование", 2013, Лекция 14
Сев. НТУ, кафедра Ки. ВТ, курс 19 "Моделирование", 2013, Лекция 14
 Игра «Жизнь» . Алгоритм 1. Для каждой ячейки выясняется ее текущее состояние и состояние соседей; 2. Далее применяется одно из трех правил игры «Жизнь» ; 3. Новое состояние ячейки записывается в двухмерный массив; 4. После обработки текущей популяции и заполнения массива значениями новой популяцией, в ячейки записывается все содержимое массива. Сев. НТУ, кафедра Ки. ВТ, курс 20 "Моделирование", 2013, Лекция 14
Игра «Жизнь» . Алгоритм 1. Для каждой ячейки выясняется ее текущее состояние и состояние соседей; 2. Далее применяется одно из трех правил игры «Жизнь» ; 3. Новое состояние ячейки записывается в двухмерный массив; 4. После обработки текущей популяции и заполнения массива значениями новой популяцией, в ячейки записывается все содержимое массива. Сев. НТУ, кафедра Ки. ВТ, курс 20 "Моделирование", 2013, Лекция 14
 «Сахарная» модель Предложена Джошуа Эпштейном и Робертом Экстеллом (Epstein, Axtell (1996)). Имеется некоторая окружающая среда — сахарный ландшафт, где в двумерном пространстве разбросан сахар – количество сахара – случайная величина; туда же помещены агенты-жуки, которые ползают по сахарному ландшафту по простым правилам: агенту надо есть сахар, и он перемещается туда, где сахара больше. Сев. НТУ, кафедра Ки. ВТ, курс 21 "Моделирование", 2013, Лекция 14
«Сахарная» модель Предложена Джошуа Эпштейном и Робертом Экстеллом (Epstein, Axtell (1996)). Имеется некоторая окружающая среда — сахарный ландшафт, где в двумерном пространстве разбросан сахар – количество сахара – случайная величина; туда же помещены агенты-жуки, которые ползают по сахарному ландшафту по простым правилам: агенту надо есть сахар, и он перемещается туда, где сахара больше. Сев. НТУ, кафедра Ки. ВТ, курс 21 "Моделирование", 2013, Лекция 14
 «Сахарная» модель. Правила Пространство. - Двумерная решетка; - В каждой клетке указано текущее количество сахара и максимально возможное; - Распределение сахара по пространству; - Количество сахара в клетке восстанавливается до максимального уровня с заданным темпом. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 14 22
«Сахарная» модель. Правила Пространство. - Двумерная решетка; - В каждой клетке указано текущее количество сахара и максимально возможное; - Распределение сахара по пространству; - Количество сахара в клетке восстанавливается до максимального уровня с заданным темпом. Сев. НТУ, кафедра Ки. ВТ, курс "Моделирование", 2013, Лекция 14 22
 «Сахарная» модель. Правила Поведение агентов. - указывается скорость потребления сахара (метаболизм); - Указывается сколько сахара можно переносить из клетки в клетку (переменная величина); - Перемещается в ближайшую пустую клетку с мах количеством сахара; - Агент погибает, если ему нечего есть, при этом в произвольной пустой клетке генерируется новый. Сев. НТУ, кафедра Ки. ВТ, курс 23 "Моделирование", 2013, Лекция 14
«Сахарная» модель. Правила Поведение агентов. - указывается скорость потребления сахара (метаболизм); - Указывается сколько сахара можно переносить из клетки в клетку (переменная величина); - Перемещается в ближайшую пустую клетку с мах количеством сахара; - Агент погибает, если ему нечего есть, при этом в произвольной пустой клетке генерируется новый. Сев. НТУ, кафедра Ки. ВТ, курс 23 "Моделирование", 2013, Лекция 14
 «Сахарная» модель. Исследования - распределение «богатства» между агентами; - Агенты имеют конечный срок жизни. Рост и распределение по возрастам населения; - Миграция ; - Учет загрязнения окружающей среды. Агент выбирает клетку, в которой отношение количества сахара к загрязнению максимально. - Правила наследования. На основе моделей искусственного общества строятся реальные экономические модели. 24
«Сахарная» модель. Исследования - распределение «богатства» между агентами; - Агенты имеют конечный срок жизни. Рост и распределение по возрастам населения; - Миграция ; - Учет загрязнения окружающей среды. Агент выбирает клетку, в которой отношение количества сахара к загрязнению максимально. - Правила наследования. На основе моделей искусственного общества строятся реальные экономические модели. 24
 Модель «Социальная сеть» Имеется N агентов. Каждый агент i характеризуется числом ai, показывающим его привлекательность для других агентов, (0 < ai < 1). Заранее ai неизвестно. Выявляется в процессе взаимодействий. Для простоты осуществления процесса имитации заданная привлекательность распределяется равномерно. Сев. НТУ, кафедра Ки. ВТ, курс 25 "Моделирование", 2013, Лекция 14
Модель «Социальная сеть» Имеется N агентов. Каждый агент i характеризуется числом ai, показывающим его привлекательность для других агентов, (0 < ai < 1). Заранее ai неизвестно. Выявляется в процессе взаимодействий. Для простоты осуществления процесса имитации заданная привлекательность распределяется равномерно. Сев. НТУ, кафедра Ки. ВТ, курс 25 "Моделирование", 2013, Лекция 14
 Модель «Социальная сеть» . Формальная постановка задачи a — номер человека (agent); A — множество (номеров) агентов, составляющих искусственное общество; t — номер интервала времени; m — номер действия, которое может производить агент; ma(t) — действие, осуществляемое агентом a в интервале времени t (натуральное число); Сев. НТУ, кафедра Ки. ВТ, курс 26 "Моделирование", 2013, Лекция 14
Модель «Социальная сеть» . Формальная постановка задачи a — номер человека (agent); A — множество (номеров) агентов, составляющих искусственное общество; t — номер интервала времени; m — номер действия, которое может производить агент; ma(t) — действие, осуществляемое агентом a в интервале времени t (натуральное число); Сев. НТУ, кафедра Ки. ВТ, курс 26 "Моделирование", 2013, Лекция 14
 Модель «Социальная сеть» . Формальная постановка задачи M — множество возможных действий (номеров этих действий), которые могут в принципе осуществлять люди. Элемент множества М – порядковое число m, под которым фигурирует данное действие; D — подмножество множества A, людей, осуществляющих взаимодействие между собой в процессе своей деятельности; Сев. НТУ, кафедра Ки. ВТ, курс 27 "Моделирование", 2013, Лекция 14
Модель «Социальная сеть» . Формальная постановка задачи M — множество возможных действий (номеров этих действий), которые могут в принципе осуществлять люди. Элемент множества М – порядковое число m, под которым фигурирует данное действие; D — подмножество множества A, людей, осуществляющих взаимодействие между собой в процессе своей деятельности; Сев. НТУ, кафедра Ки. ВТ, курс 27 "Моделирование", 2013, Лекция 14
 Модель «Социальная сеть» . Формальная постановка задачи Da(t) — взаимодействие, в котором участвует человек a в момент времени t; Одно и тоже подмножество людей может осуществлять разные взаимодействия. Внешне наблюдаемое состояние общества в данный момент времени: множество пар[действие ma(t), взаимодействие Da(t)], для всех а. Сев. НТУ, кафедра Ки. ВТ, курс 28 "Моделирование", 2013, Лекция 14
Модель «Социальная сеть» . Формальная постановка задачи Da(t) — взаимодействие, в котором участвует человек a в момент времени t; Одно и тоже подмножество людей может осуществлять разные взаимодействия. Внешне наблюдаемое состояние общества в данный момент времени: множество пар[действие ma(t), взаимодействие Da(t)], для всех а. Сев. НТУ, кафедра Ки. ВТ, курс 28 "Моделирование", 2013, Лекция 14

