Agenda Questions Topics IDA

Agenda • Questions? • Topics – IDA* – Hill climbing (restarts etc) – CSP (Revisit forward checking; iterative appraoches for CSP)

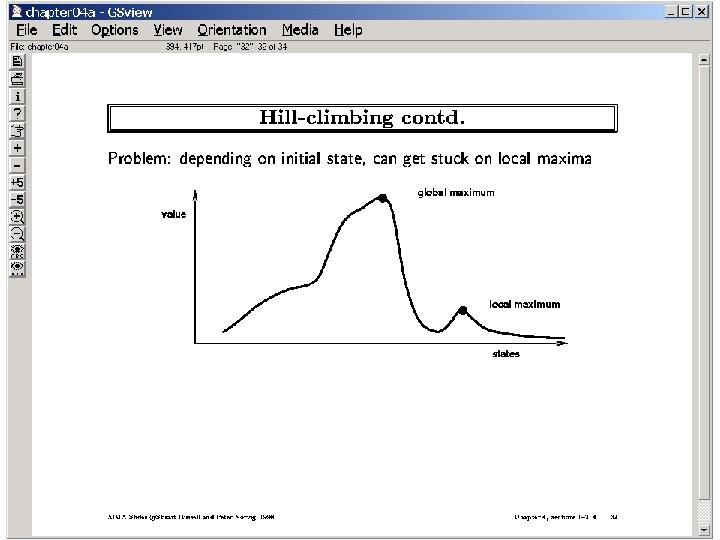
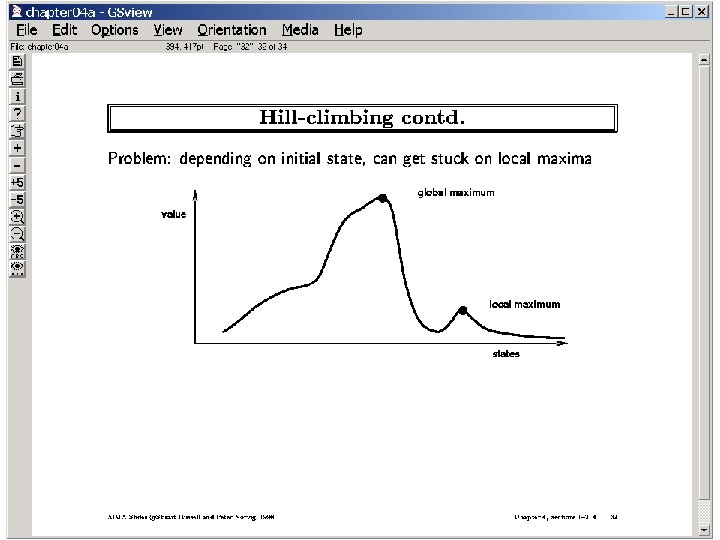
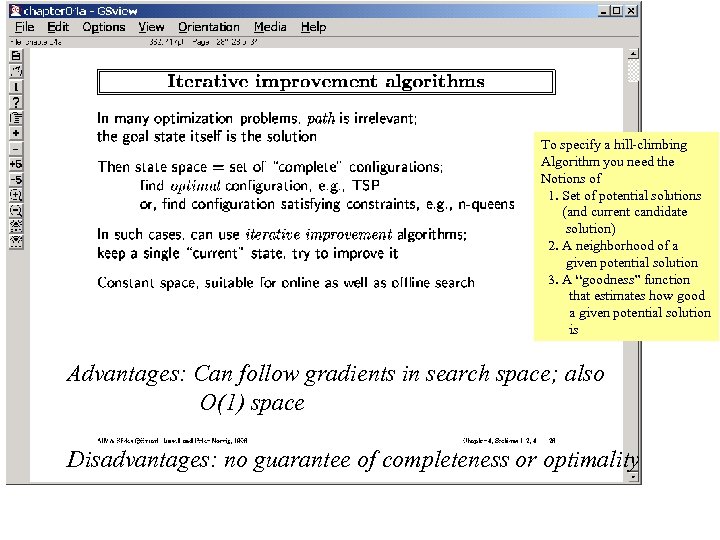To specify a hill-climbing Algorithm you need the Notions of 1. Set of potential solutions (and current candidate solution) 2. A neighborhood of a given potential solution 3. A “goodness” function that estimates how good a given potential solution is Advantages: Can follow gradients in search space; also O(1) space Disadvantages: no guarantee of completeness or optimality

In practice, the main issue is the schedule used to decrease T. The faster T is decreased, the faster the search, but the lower The probability of reaching global optimum.

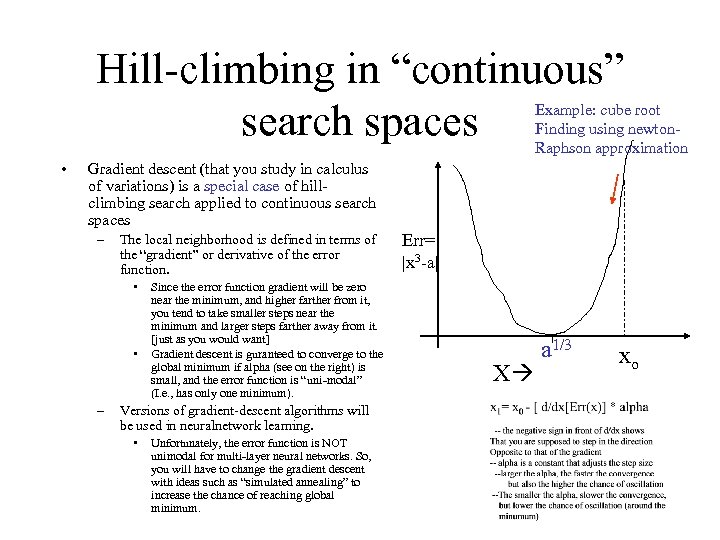Hill-climbing in “continuous” search spaces Example: cube root Finding using newton. Raphson approximation • Gradient descent (that you study in calculus of variations) is a special case of hillclimbing search applied to continuous search spaces – The local neighborhood is defined in terms of the “gradient” or derivative of the error function. • • – Since the error function gradient will be zero near the minimum, and higher farther from it, you tend to take smaller steps near the minimum and larger steps farther away from it. [just as you would want] Gradient descent is guranteed to converge to the global minimum if alpha (see on the right) is small, and the error function is “uni-modal” (I. e. , has only one minimum). Versions of gradient-descent algorithms will be used in neuralnetwork learning. • Unfortunately, the error function is NOT unimodal for multi-layer neural networks. So, you will have to change the gradient descent with ideas such as “simulated annealing” to increase the chance of reaching global minimum. Err= |x 3 -a| X a 1/3 xo

The middle ground between hill-climbing and systematic search • Hill-climbing has a lot of freedom in deciding which node to expand next. But it is incomplete even for finite search spaces. – Good for problems which have solutions, but the solutions are nonuniformly clustered. • Systematic search is complete (because its search tree keeps track of the parts of the space that have been visited). – Good for problems where solutions may not exist, • Or the whole point is to show that there are no solutions (e. g. propositional entailment problem to be discussed later). – or the state-space is densely connected (making repeated exploration of states a big issue). Smart idea: Try the middle ground between the two?

Between Hill-climbing and systematic search • You can reduce the freedom of hill-climbing search to make it more complete – Tabu search • You can increase the freedom of systematic search to make it more flexible in following local gradients – Random restart search

Tabu Search • A variant of hill-climbing search that attempts to reduce the chance of revisiting the same states – Idea: • Keep a “Tabu” list of states that have been visited in the past. • Whenever a node in the local neighborhood is found in the tabu list, remove it from consideration (even if it happens to have the best “heuristic” value among all neighbors) – Properties: • As the size of the tabu list grows, hill-climbing will asymptotically become “non-redundant” (won’t look at the same state twice) • In practice, a reasonable sized tabu list (say 100 or so) improves the performance of hill climbing in many problems

Random restart search • Variant of depth-first search where – When a node is expanded, its children are first randomly permuted before being introduced into the open list • The permutation may well be “biased” random permutation – Search is “restarted” from scratch anytime a “cutoff” parameter is exceeded • There is a “Cutoff” (which may be in terms of # of backtracks, #of nodes expanded or amount of time elapsed) • Properties: – Because of the “random” permutation, everytime the search is restarted, you are likely to follow different paths through the search tree. This allows you to recover from the bad initial moves. – The higher the cutoff value the lower the amount of restarts (and thus the lower the “freedom” to explore different paths). • When cutoff is infinity, random restart search is just normal depth-first search—it will be systematic and complete • For smaller values of cutoffs, the search has higher freedom, but no guarantee of completeness • A strategy to guarantee asymptotic completeness: (***Didn’t say this in the class) – Start with a low cutoff value, but keep increasing it as time goes on. – Random restart search has been shown to be very good for problems that have a reasonable percentage of “easy to find” solutions (such problems are said to exhibit “heavy-tail” phenomenon). Many real-world problems have this property.

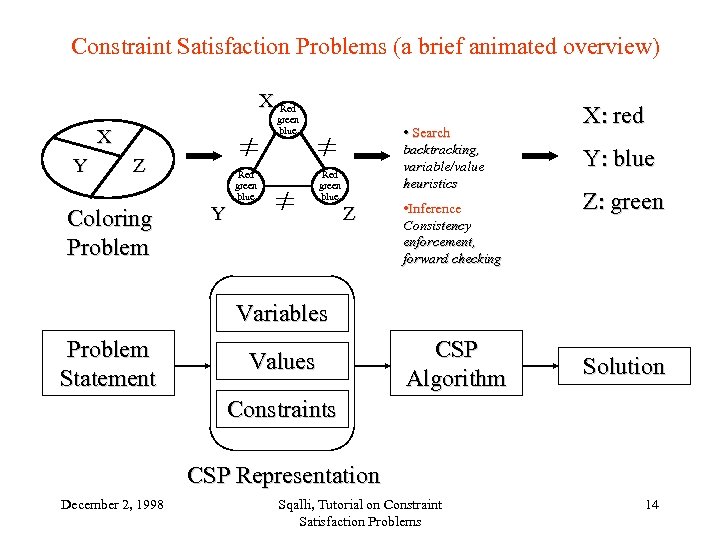Constraint Satisfaction Problems (a brief animated overview) X Red green blue X Y Z Coloring Problem Red green blue • Search backtracking, variable/value heuristics Red green blue Y Z • Inference Consistency enforcement, forward checking X: red Y: blue Z: green Variables Problem Statement Values CSP Algorithm Solution Constraints CSP Representation December 2, 1998 Sqalli, Tutorial on Constraint Satisfaction Problems 14

Class of 20 th September, 2001 Any qns on HW 2? Project 1? Lecture?

Agenda • • • Questions on project 1? (due Sep 27 th ) Questions on homework 2? (due Sep 25 th) Any other questions? Lecture Next class: Adversarial Search (Chapter 6) – CSP was in Chapter 5 – Hill-climbing/Genetic algorithms in Chapter 4

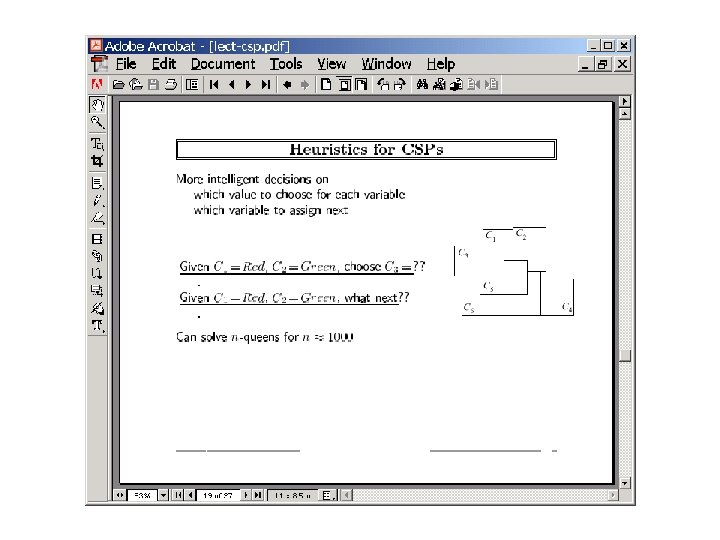
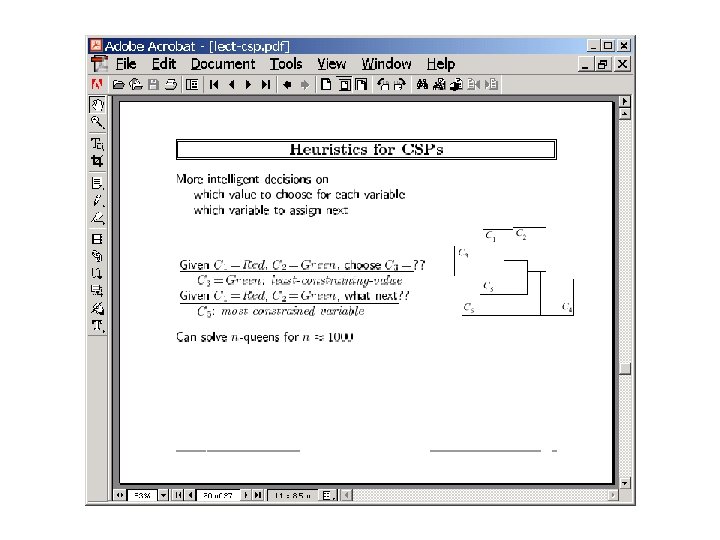
Review of CSP/SAT concepts • Constraint Satisfaction Problem (CSP) – Given • A set of discrete variables • Legal domains for each of the variables • A set of constraints on values groups of variables can take – Find an assignment of values to all the variables so that none of the constraints are violated • SAT Problem = CSP with boolean variables x, y, u, v: {A, B, C, D, E} w: {D, E} l : {A, B} x=A w E y=B u D u=C l A v=D l B A solution: x=B, y=C, u=D, v=E, w=D, l=B x¬A N 1: {x=A} y¬ B N 2: {x= A & y = B } v¬ D N 3: {x= A & y = B & v = D } u¬ C N 4: {x= A & y = B & v = D & u = C } w¬ E N 5: {x= A & y = B & v = D & u = C & w= E } w¬ D N 6: {x= A & y = B & v = D & u = C & w= D }

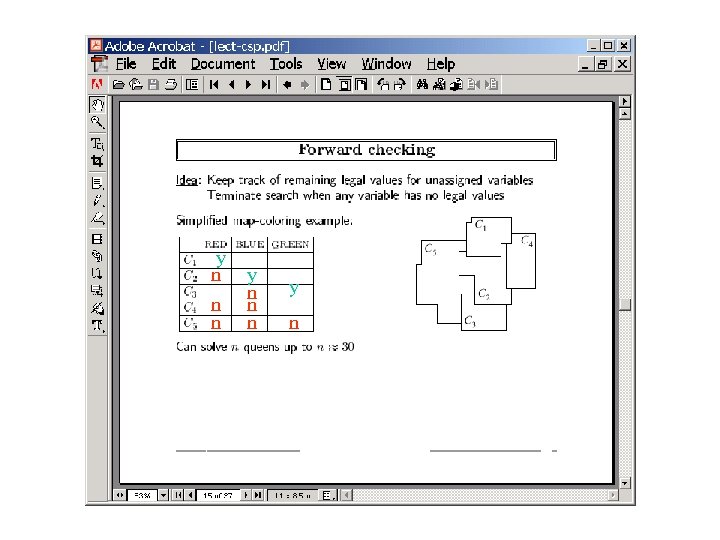y n n n y n

Dynamic variable ordering • Do forward checking • Order variables based on their “live” domains

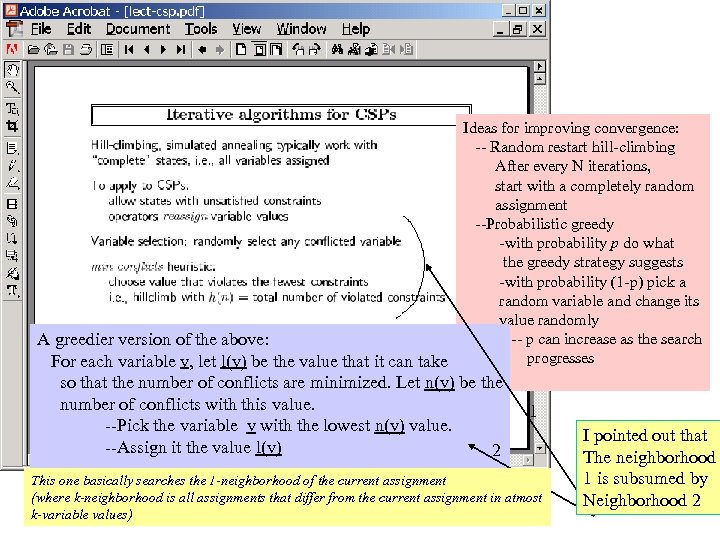Ideas for improving convergence: -- Random restart hill-climbing After every N iterations, start with a completely random assignment --Probabilistic greedy -with probability p do what the greedy strategy suggests -with probability (1 -p) pick a random variable and change its value randomly -- p can increase as the search A greedier version of the above: progresses For each variable v, let l(v) be the value that it can take so that the number of conflicts are minimized. Let n(v) be the number of conflicts with this value. --Pick the variable v with the lowest n(v) value. --Assign it the value l(v) 2 1 This one basically searches the 1 -neighborhood of the current assignment (where k-neighborhood is all assignments that differ from the current assignment in atmost k-variable values) I pointed out that The neighborhood 1 is subsumed by Neighborhood 2

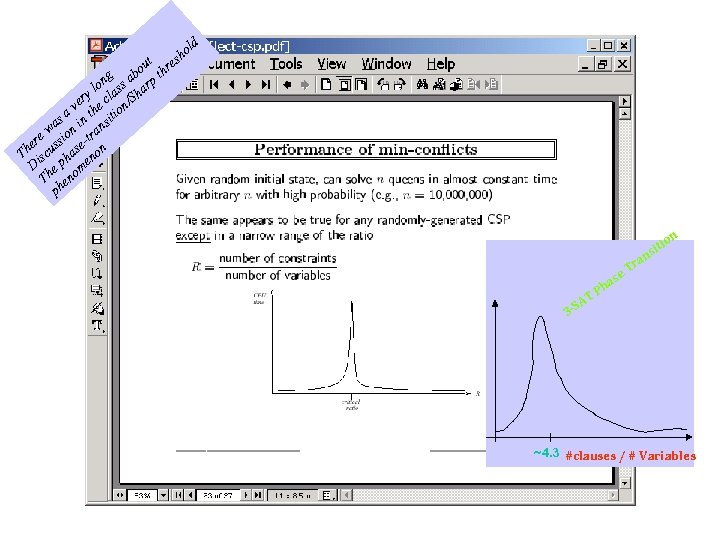ld ho s ut re bo th ng a lo ass harp ry l S ve he c on/ a t ti as n in nsi w a re ssio e-tr e u s Th isc ha non D e p ome Th en ph on iti ns ra T se a T -SA 3 Ph ~4. 3 #clauses / # Variables

Class of 25 th September, 2001

Announcements • Project – “Late” submission allowed until 4 th october with 10% penalty • Homework 2 – “Late” submission allowed until 27 th September with 5% penalty • Midterm – Oct 9 th or 11 th (most likely in-class) • Don’t print hidden slides in lecture notes. (use the powerpoint print option to supress hidden slides while printing ) • I often modify/add slides after the class to reflect additional discussion done in the class.

Agenda 1. Local consistency in CSP 2. Genetic algorithms (variation of Hill Climbing) 3. IDA* search 4. Pattern database heuristics 5. ---Start adversarial search…

What makes CSP problems hard? Asignments to individual variables that seem locally consistent are often globally infeasible, causing costly backtracking. The difficulty of a CSP/SAT problem depends on Not very predictive. For example, even if there are too – Number of variables Many variables, the problem may still be easy because (propositions) The constraints are “very few” OR “Very many” Relative to # variables. – Number of constraints Similarly it may be the case that an n-ary constraint really (clauses) Is decomposable into several k-ary constratins (k<

Hardness & Local Consistency • An n-variable CSP problem is said to be k-consistent iff every consistent assignment for (k-1) of the n variables can be extended to include any k-th variable • Directional consistency: Assignment to first k-1 variables can be extended to the k-th variable • Strongly k-consistent if it is j-consistent for all j from 1 to k • Higher the level of (strong) consistency of problem, the lesser the amount of backtracking required to solve the problem – A CSP with strong n-consistency can be solved without any backtracking • We can improve the level of consistency of a problem by explicating implicit constraints – Enforcing k-consistency is of O(nk) complexity • Break-even seems to be around k=2 (“arc consistency”) or 3 (“path consistency”) • Use of directional and partial consistency enforcement techniques –

ke ma ay e ic is m ce w l log h n a ft e o nse O sition Som re se ropo mo uss P c dis • In general, enforcing consistency involves explicitly adding constraints that hold given the existing constraints – E. g. In enforcing 3 -consistency if we find that for a particular 2 -label {xi=v 1 & xj=v 2} there is no possible consistent value of xk, then we write this as an additional constraint • {xi=v 1}=> {xj != v 2} – When enforcing 2 -consistency (or arc-consistency), the new constraints will be of the form xi!=v 1 , and so these can be represented by just contracting the domain of xi by pruning v 1 from it • Unearthing implicit constraints can also be interpreted as “inferring” new constraints that hold given the existing constraints. – In the context of boolean CSPs (I. e. , propositional satisfiability problems), the analogy is even more striking since unearthing new constraints means writing down new clauses (or “facts”) that hold given the existing clauses – This interpretation shows that consistency enforcement is a form of “inference” process. – There is a general idea that in solving a search problem, you can interleave two different processes • “inference” trying to either infer the solution itself or saying no solution exists • “conditioning or enumeration”which attempts to systematically go through potential solutions looking for a real solution. – Good search algorithms interleave both inference and conditioning • E. g. the CSP algorithm we discussed in the class uses backtracking search (enumeration), and forward checking (inference). More comments made in the class ADDED AFTER CLASS IMPORTANT

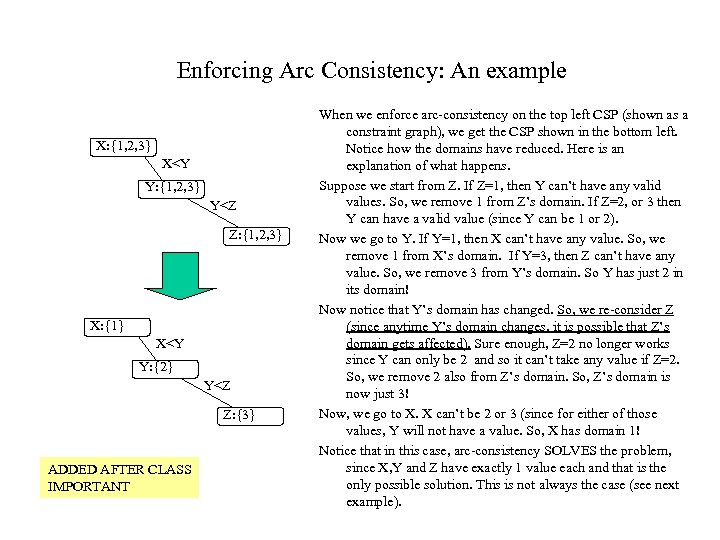Enforcing Arc Consistency: An example X: {1, 2, 3} X

More on arc-consistency Arc-consistency doesn’t always imply that the CSP has a solution or that there is no search required. In the previous example, if each variable had domains 1, 2, 3, 4, then at the end of enforcing arc-consistency, each variable will still have 2 values in its domain—thus necessitating search. Here is another example which shows that the search may find that there is no solution for the CSP, even though it is arc-consistent. ADDED AFTER CLASS IMPORTANT Here is a binary CSP that Is arc-consistent but has no Solution.

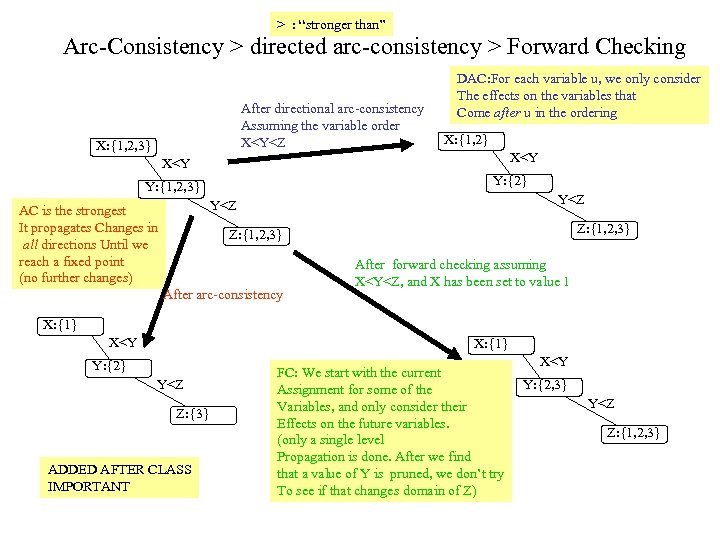> : “stronger than” Arc-Consistency > directed arc-consistency > Forward Checking After directional arc-consistency Assuming the variable order X

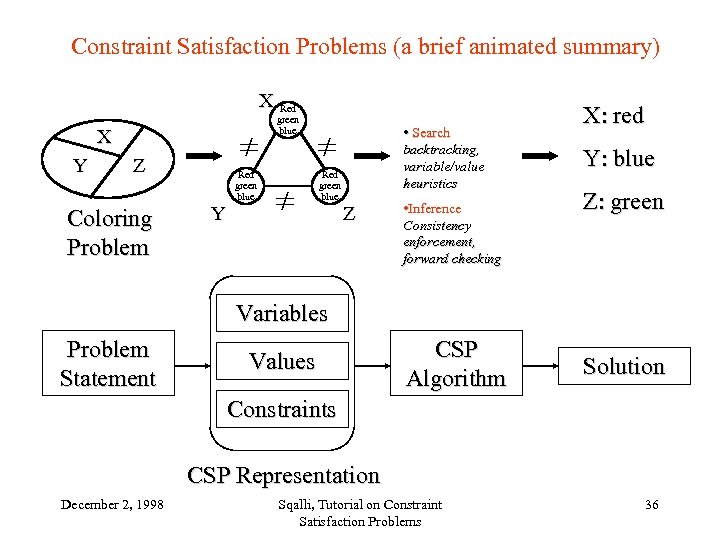Constraint Satisfaction Problems (a brief animated summary) X Red green blue X Y Z Coloring Problem Red green blue • Search backtracking, variable/value heuristics Red green blue Y Z • Inference Consistency enforcement, forward checking X: red Y: blue Z: green Variables Problem Statement Values CSP Algorithm Solution Constraints CSP Representation December 2, 1998 Sqalli, Tutorial on Constraint Satisfaction Problems 36

Genetic Algorithms Does the evolutionary metaphor really buy us anything? -A form of hill climbing --differences: Multiple current nodes (seeds) (instead of a single one) Neighborhood defined in terms of combination of current seeds --with some randomness A bit of “evolutionary” metaphors

Class of 27 th September, 2001

IDA* to handle the A* memory problem • Basicaly IDDFS, except instead of the iterations being defined in terms of depth, we define it in terms of f-value – Start with the f cutoff equal to the f-value of the root node – Loop • Generate and search all nodes whose f-values are less than or equal to current cutoff. – Use depth-first search to search the trees in the individual iterations – Keep track of the node N’ which has the smallest fvalue that is still larger than the current cutoff. Let this f-value be next-largest-f-value -- If the search finds a goal node, terminate. If not, set cutoff = next-largest-f-value and go back to Loop Properties: Linear memory. #Iterations in the worst case? = Bd !! (Happens when all nodes have distinct f-values)

Pattern Databases and other more sophisticated approaches for deriving heuristics

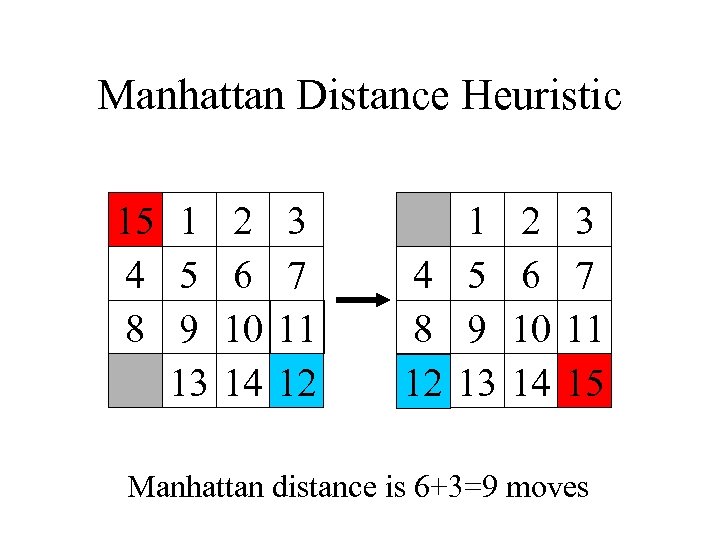Manhattan Distance Heuristic 15 1 2 3 4 5 6 7 8 9 10 11 13 14 12 1 4 5 8 9 12 13 2 6 10 14 3 7 11 15 Manhattan distance is 6+3=9 moves

Performance on 15 Puzzle • Random 15 puzzle instances were first solved optimally using IDA* with Manhattan distance heuristic (Korf, 1985). • Optimal solution lengths average 53 moves. • 400 million nodes generated on average. • Average solution time is about 50 seconds on current machines.

Limitation of Manhattan Distance • To solve a 24 -Puzzle instance, IDA* with Manhattan distance would take about 65, 000 years on average. • Assumes that each tile moves independently • In fact, tiles interfere with each other. • Accounting for these interactions is the key to more accurate heuristic functions.

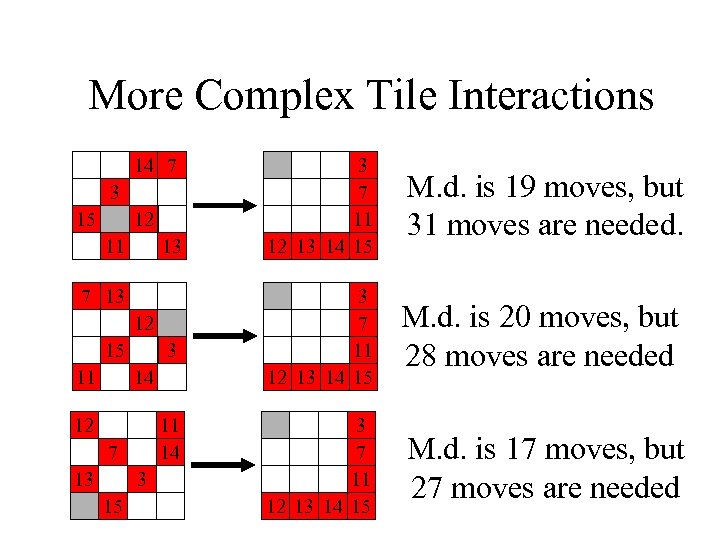More Complex Tile Interactions 14 7 3 15 12 11 13 7 13 12 15 11 3 14 12 11 14 7 13 3 15 3 7 11 12 13 14 15 M. d. is 19 moves, but 31 moves are needed. 3 7 11 12 13 14 15 M. d. is 20 moves, but 28 moves are needed 3 7 11 12 13 14 15 M. d. is 17 moves, but 27 moves are needed

Pattern Database Heuristics • Culberson and Schaeffer, 1996 • A pattern database is a complete set of such positions, with associated number of moves. • e. g. a 7 -tile pattern database for the Fifteen Puzzle contains 519 million entries.

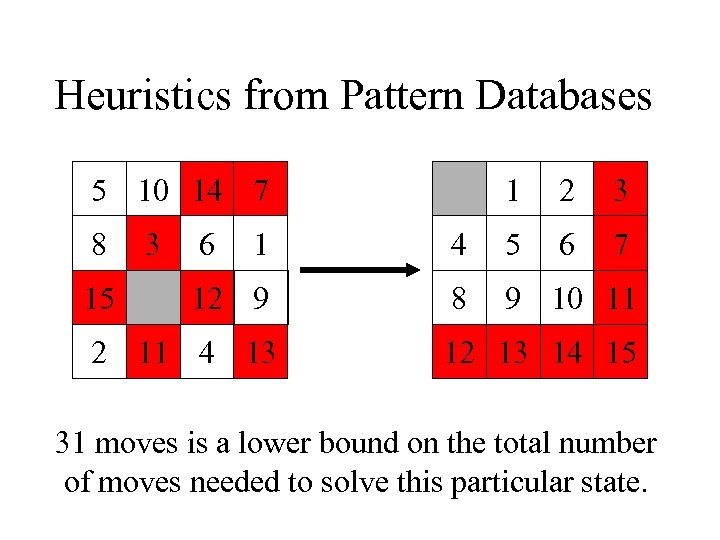Heuristics from Pattern Databases 5 10 14 7 8 15 3 6 1 2 3 6 7 1 4 5 12 9 8 9 10 11 2 11 4 13 12 13 14 15 31 moves is a lower bound on the total number of moves needed to solve this particular state.

Precomputing Pattern Databases • Entire database is computed with one backward breadth-first search from goal. • All non-pattern tiles are indistinguishable, but all tile moves are counted. • The first time each state is encountered, the total number of moves made so far is stored. • Once computed, the same table is used for all problems with the same goal state.

What About the Non-Pattern Tiles? • Given more memory, we can compute additional pattern databases from the remaining tiles. • In fact, we can compute multiple pattern databases from overlapping sets of tiles. • The only limit is the amount of memory available to store the pattern databases.

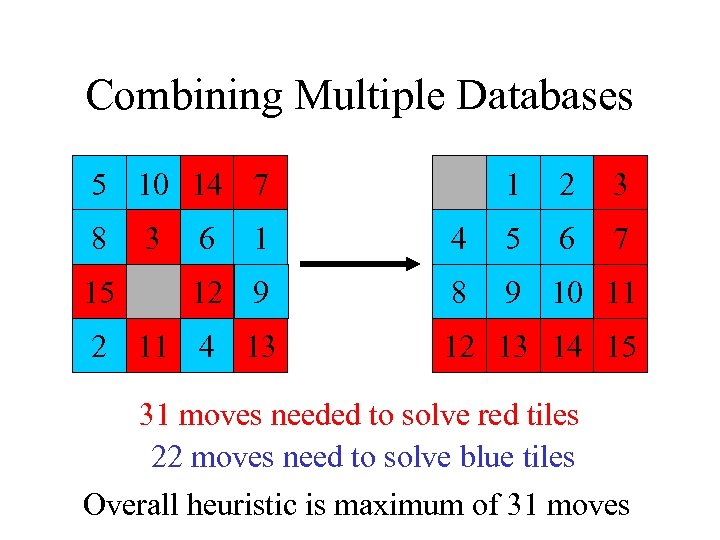Combining Multiple Databases 5 10 14 7 8 15 3 6 1 2 3 6 7 1 4 5 12 9 8 9 10 11 2 11 4 13 12 13 14 15 31 moves needed to solve red tiles 22 moves need to solve blue tiles Overall heuristic is maximum of 31 moves

Applications of Pattern Databases • On 15 puzzle, IDA* with pattern database heuristics is about 10 times faster than with Manhattan distance (Culberson and Schaeffer, 1996). • Pattern databases can also be applied to Rubik’s Cube.

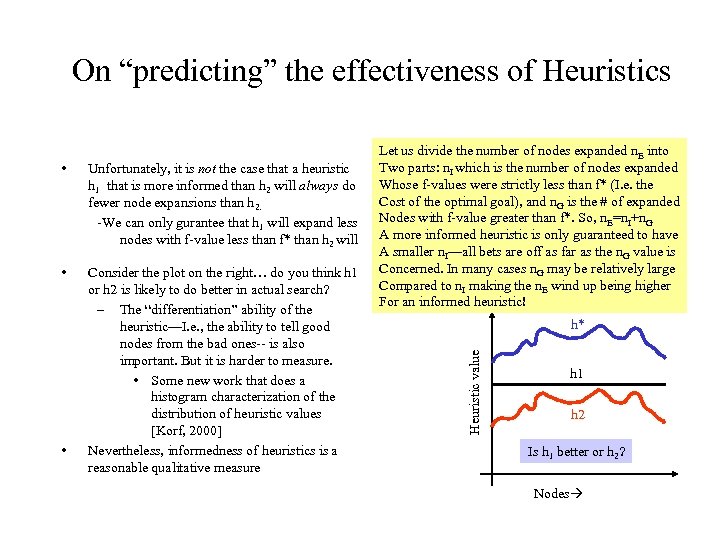On “predicting” the effectiveness of Heuristics Unfortunately, it is not the case that a heuristic h 1 that is more informed than h 2 will always do fewer node expansions than h 2. -We can only gurantee that h 1 will expand less nodes with f-value less than f* than h 2 will • Consider the plot on the right… do you think h 1 or h 2 is likely to do better in actual search? – The “differentiation” ability of the heuristic—I. e. , the ability to tell good nodes from the bad ones-- is also important. But it is harder to measure. • Some new work that does a histogram characterization of the distribution of heuristic values [Korf, 2000] Nevertheless, informedness of heuristics is a reasonable qualitative measure • h* Heuristic value • Let us divide the number of nodes expanded n. E into Two parts: n. I which is the number of nodes expanded Whose f-values were strictly less than f* (I. e. the Cost of the optimal goal), and n. G is the # of expanded Nodes with f-value greater than f*. So, n. E=n. I+n. G A more informed heuristic is only guaranteed to have A smaller n. I—all bets are off as far as the n. G value is Concerned. In many cases n. G may be relatively large Compared to n. I making the n. E wind up being higher For an informed heuristic! h 1 h 2 Is h 1 better or h 2? Nodes