Adversaries and Information Leaks Geoffrey Smith Florida International

Adversaries and Information Leaks Geoffrey Smith Florida International University November 7, 2007 TGC 2007 Workshop on the Interplay of Programming Languages and Cryptography 1

Motivation n Suppose that a program c processes some sensitive information. n How do we know that c will not leak the information, either accidentally or maliciously? n How can we ensure that c is trustworthy ? n Secure information flow analysis: Do a static analysis (e. g. type checking) on c prior to executing it. 2

Two Adversaries n The program c: n Has direct access to the sensitive information (H variables) n Behavior is constrained by the static analysis n The observer O of c’s public output: n n Has direct access only to c’s public output (final values of L variables, etc. ) Behavior is unconstrained (except for computational resource bounds) 3

The Denning Restrictions n Classification: An expression is H if it contains any H variables; otherwise it is L. n Explicit flows: A H expression cannot be assigned to a L variable. n Implicit flows: A guarded command with a H guard cannot assign to L variables. if ((secret % 2) == 0) leak = 0; else leak = 1; H guard assignment to L variable 4

Noninterference n If c satisfies the Denning Restrictions, then (assuming c always terminates) the final values of L variables are independent of the initial values of H variables. n So observer O can deduce nothing about the initial values of H variables. n Major practical challenge: How can we relax noninterference to allow “small” information leaks, while still preserving security? 5

Talk Outline I. Secure information flow for a language with encryption [FMSE’ 06] II. Termination leaks in probabilistic programs [PLAS’ 07] III. Foundations for quantitative information flow Joint work with Rafael Alpízar. 6

I. Secure information flow for a language with encryption n Suppose that E and D denote encryption and decryption with a suitably-chosen shared key K. n Programs can call E and D but cannot access K directly. n Intuitively, we want the following rules: If e is H, then E(e) is L. n If e is either L or H, then D(e) is H. n n But is this sound ? Note that it violates noninterference, since E(e) depends on e. 7

It is unsound if encryption is deterministic! Assume secret : H, mask : L, leak : L. leak : = 0; n-1 mask : = 2 ; while mask ≠ 0 do ( if E(secret | mask) = E(secret) then leak : = leak | mask; mask : = mask >> 1 ) 8

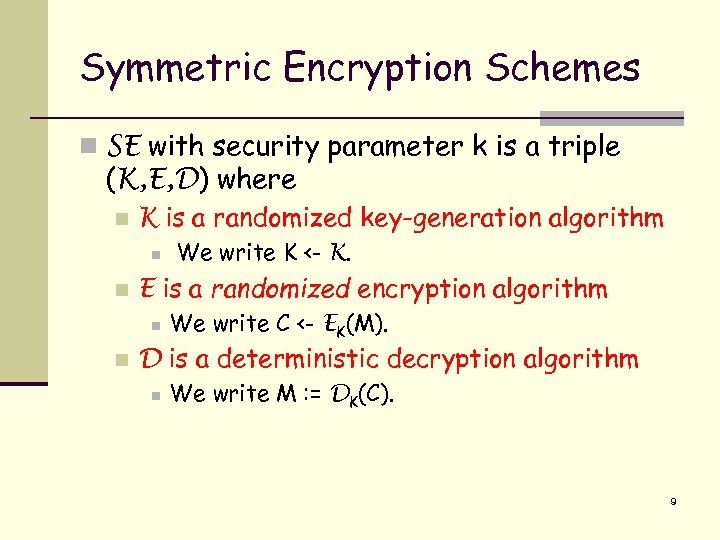Symmetric Encryption Schemes n SE with security parameter k is a triple (K, E, D) where n K is a randomized key-generation algorithm n n E is a randomized encryption algorithm n n We write K <- K. We write C <- EK(M). D is a deterministic decryption algorithm n We write M : = DK(C). 9

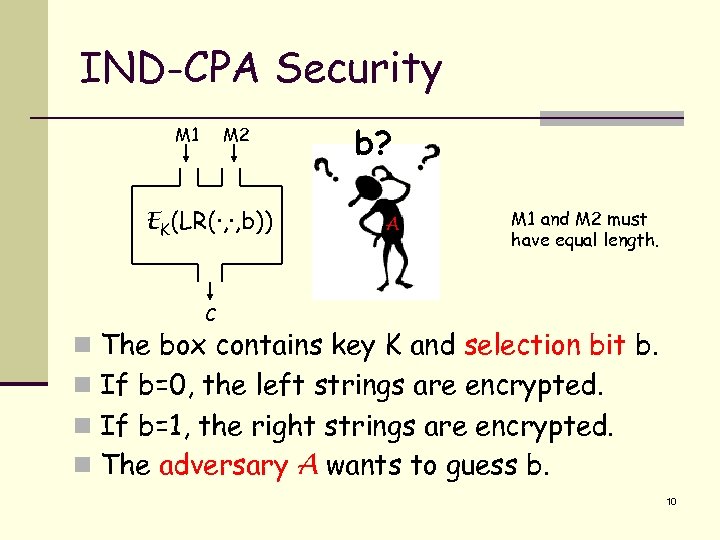IND-CPA Security M 1 M 2 EK(LR(·, ·, b)) b? A M 1 and M 2 must have equal length. C n The box contains key K and selection bit b. n If b=0, the left strings are encrypted. n If b=1, the right strings are encrypted. n The adversary A wants to guess b. 10

IND-CPA advantage n Experiment Expind-cpa-b(A) K <- K; d <- AEK(LR(·, ·, b)); return d n Advind-cpa(A) = Pr[Expind-cpa-1(A) = 1] – Pr[Expind-cpa-0(A) = 1]. n SE is IND-CPA secure if no polynomial-time adversary A can achieve a non-negligible IND-CPA advantage. 11

Our programming language n e : : = x | n | e 1+e 2 | … | D(e 1, e 2) n c : : = x : = e random assignment according to distribution R | x <- R | (x, y) <- E(e) | skip | if e then c 1 else c 2 | while e do c | c 1; c 2 n Note: n-bit values, 2 n-bit ciphertexts. 12

Our type system n Each variable is classified as H or L. n We just enforce the Denning restrictions, with modifications for the new constructs. n E(e) is L, even if e is H. n D(e 1, e 2) is H, even if e 1 and e 2 are L. n R (a random value) is L. 13

Leaking adversary B n B has a H variable h and a L variable l, and other variables typed arbitrarily. n h is initialized to 0 or 1, each with probability ½. n B can call E() and D(). n B tries to copy the initial value of h into l. 14

Leaking advantage of B n Experiment Expleak(B) K <- K; h 0 <- {0, 1}; h : = h 0; initialize other variables to 0; run BEK(·), DK(·); if l = h 0 then return 1 else return 0 n Advleak(B) = 2 · Pr[Expleak(B) = 1] - 1 15

Soundness via Reduction n For now, drop D() from the language. n Theorem: Given a well-typed leaking adversary B that runs in time p(k), there exists an IND-CPA adversary A that runs in time O(p(k)) and such that Advind-cpa(A) ≥ ½·Advleak(B). n Corollary: If SE is IND-CPA secure, then no polynomial-time, well-typed leaking adversary B achieves non-negligible advantage. 16

Proof of Theorem n Given B, construct A that runs B with a randomly-chosen 1 -bit value of h. n Whenever B calls E(e), A passes (0 n, e) to its oracle EK(LR(·, ·, b)). So if b = 1, E(e) returns EK(e). n And if b = 0, E(e) returns EK(0 n), a random number that has nothing to do with e! n n If B terminates within p(k) steps and succeeds in leaking h to l, then A guesses 1. n Otherwise A guesses 0. 17

What is A’s IND-CPA advantage? n If b = 1, B is run faithfully. n Hence Pr[Expind-cpa-1(A) = 1] = Pr[Expleak(B) = 1] = ½·Advleak(B) + ½ n If b = 0, B is not run faithfully. n Here B is just a well-typed program with random assignment but no encryption. 18

More on the b = 0 case n In this case, we expect the type system to prevent B from leaking h to l. n However, when B is run unfaithfully, it might fail to terminate! n Some careful analysis is needed to deal with this possibility — Part II of talk! n But in the end we get Pr[Expind-cpa-0(A) = 1] ≤ ½ n So Advind-cpa(A) ≥ ½·Advleak(B), as claimed. □ 19

Can we get a result more like noninterference? n Let c be a well-typed, polynomial-time program. n Let memories μ and ν agree on L variables. n Run c under either μ or ν, each with probability ½. n A noninterference adversary O is given the final values of the L variables of c. n O tries to guess which initial memory was used. 20

A computational noninterference result n Theorem: No polynomial-time adversary O (for c, μ, and ν) can achieve a non-negligible noninterference advantage. n Proof idea: Given O, we can construct a well -typed leaking adversary B. n Note that O cannot be assumed to be well typed! n But because O sees only the L variables of c, it is automatically well typed under our typing rules. 21

Construction of B initialize L variables of c according to μ and ν; if h = 0 then initialize H variables of c according to μ else initialize H variables of c according to ν; c; O; // O puts its guess into g l : = g 22

Related work n Laud and Vene [FCT 2005]. n Work on cryptographic protocols: Backes and Pfitzmann [Oakland 2005], Laud [CCS 2005], … n Askarov, Hedin, Sabelfeld [SAS’ 06] n Laud [POPL’ 08] n Vaughan and Zdancewic [Oakland’ 07] 23

II. Termination leaks in probabilistic programs n In Part I, we assumed that all adversaries run in time polynomial in k, the key size. n This might seem to be “without loss of generality” (practically speaking) since otherwise the adversary takes too long. n But what if program c either terminates quickly or else goes into an infinite loop? n In that case, observer O might quickly be able to observe whether c terminates. 24

The Denning Restrictions and Nontermination n The Denning Restrictions allow H variables to affect nontermination: while secret = 0 do skip; leak : = 1 n “If c satisfies the Denning Restrictions, then (assuming c always terminates) the final values of L variables are independent of the initial values of H variables. ” n Can we quantify such termination leaks? 25

Probabilistic Noninterference n Consider probabilistic programs with random assignment but no encryption. n Such programs are modeled as Markov chains of configurations (c, μ). n And noninterference becomes n The final probability distribution on L variables is independent of the initial values of H variables. 26

A program that violates probabilistic noninterference t <- {0, 1}; if t =0 then while h = 1 do skip; l : = 0 else while h = 0 do skip; l : = 1 randomly assign 0 or 1 to t t: L h: H l: L n If h = 0, terminates with l = 0 with probability ½ and loops with probability ½. n If h = 1, terminates with l = 1 with probability ½ and loops with probability ½. 27

Approximate probabilistic noninterference n Theorem: If c satisfies the Denning restrictions and loops with probability at most p, then c’s deviation from probabilistic noninterference is at most 2 p. n In our example, p = ½, and the deviation is |½ - 0| + |0 – ½| = 1 = 2 p. probability that l = 0 when h = 0 and when h = 1 probability that l = 1 when h =0 and when h = 1 28

Stripped program c n Replace all subcommands that don’t assign to L variables with skip. n Note: c contains no H variables. t <- {0, 1}; if t =0 then while h = 1 do skip; l : = 0 else while h = 0 do skip; l : = 1 t <- {0, 1}; if t =0 then skip; l : = 0 else skip; l : = 1 29

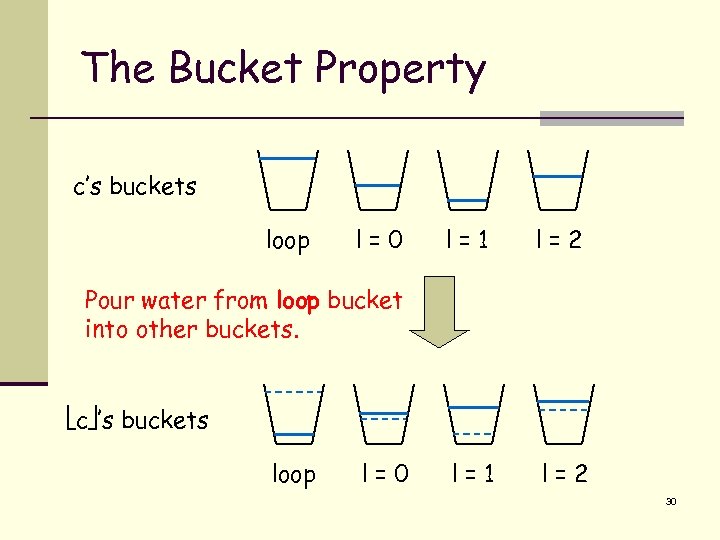The Bucket Property c’s buckets loop l=0 l=1 l=2 Pour water from loop bucket into other buckets. c ’s buckets loop l=0 30

Proof technique n In prior work on secure information flow, probabilistic bisimulation has often been useful. n Here we use a probabilistic simulation [Jonsson and Larson 1991] instead. n We define a modification of the weak simulation considered by [Baier, Katoen, Hermanns, Wolf 2005]. 31

Fast Simulation on a Markov chain (S, P) n A fast simulation R is a binary relation on S such that if s 1 R s 2 then the states reachable in one step from s 1 can be partitioned into U and V such that n n v R s 2 for every v Є V letting K = ΣuЄUP(s 1, u), if K > 0 then there exists a function Δ : S x S -> [0, 1] with n n n Δ(u, w) > 0 implies that u R w P(s 1, u)/K = ΣwЄSΔ(u, w) for all u Є U P(s 2, w) = ΣuЄUΔ(u, w) for all w Є S. 32

Proving the Bucket Property n Given R, a set T is upwards closed if sЄT and s. Rs’ implies s’ЄT. n Pr(s, n, T) is the probability of going from s to a state in T in at most n steps. n Theorem: If R is a fast simulation, T is upwards closed, and s 1 R s 2, then Pr(s 1, n, T) ≤ Pr(s 2, n, T) for every n. n We can define a fast simulation RL such that (c, μ) RL ( c , μ), for any well-typed c. 33

Approximate noninterference (c, μ) at most p loop l=0 l=1 l=2 ( c , μ) = ( c , ν) μ and ν agree on L variables (c, ν) at most p 34

Remarks n Observer O’s ability to distinguish μ and ν by statistical hypothesis testing could be bounded as in [Di Pierro, Hankin, Wiklicky 2002]. n The Bucket Property is also crucial to the soundness proof of the type system considered in Part I of this talk. 35

III. Foundations for quantitative information flow n To allow “small” information leaks, we need a quantitative theory of information. n Quite a lot of recent work: Clark, Hunt, Malacaria [2002, 2005, 2007] n Köpf and Basin [CCS’ 07] n Clarkson, Myers, Schneider [CSFW’ 05] n Lowe [CSFW’ 02] n Di Pierro, Hankin, Wiklicky [CSFW’ 02] n 36

Research Steps 1. Define a quantitative notion of information flow. 2. Show that the notion gives appropriate security guarantees. 3. Devise static analyses to enforce a given quantitative flow policy. 4. Prove the soundness of the analyses. Here we’ll discuss only steps 1 and 2. 37

Our Conceptual Framework n Rather than trying to tackle the general problem, let’s consider important special cases to better see what’s going on. n Assume that secret h is chosen from some space S with some a priori distribution. n Assume that c is a program that has only h as input and (maybe) leaks information about h to its unique public output l. n Assume that c is deterministic and total. 38

Then… [Köpf Basin 07] n There exists a function f such that l = f(h). n f induces an equivalence relation on S. n h 1 ~ h 2 iff f(h 1) = f(h 2) n So c partitions S into equivalence classes: f-1(l 3) f-1(l 1) f-1(l 2) 39

What is leaked? n The observer O sees the final value of l. n This tells O which equivalence class h belonged to. n How bad is that? n Extreme 1: If f is a constant function, then there is just one equivalence class, and noninterference holds. n Extreme 2: If f is one-to-one, then the equivalence classes are singletons, and we have total leakage of h (in principle…). 40

Quantitative Measures n Consider a discrete random variable X whose values have probabilities p 1, p 2, p 3, … n Assume pi ≥ pi+1 n Shannon Entropy H(X) = Σ pi log (1/pi) “uncertainty” about X n expected number of bits to transmit X n n Guessing Entropy G(X) = Σ i pi n expected number of guesses to guess X 41

Shannon Entropy applied to the partitions induced by c n Let’s assume that n |S| = n and h is uniformly distributed n The partition has r equivalence classes C 1, C 2, …, Cr and |Ci| = ni n H(h) = log n n “initial uncertainty about h” n H(l) = ∑ (ni/n) log (n/ni) n Plausibly, “amount of information leaked” n Extreme 1: H(l) = 0 n Extreme 2: H(l) = log n 42

How much uncertainty about h remains after the attack? n This can be calculated as a conditional Shannon entropy: n H(h|l) = ∑ (ni/n) H(Ci) = ∑ (ni/n) log ni Extreme 1: H(h|l) = log n n Extreme 2: H(h|l) = 0 n n There is a pretty equation relating these! n H(h) = H(l) + H(h|l) initial uncertainty information leaked remaining uncertainty 43

So is Step 1 finished? n “ 1. Define a quantitative notion of information flow” n In the special case that we are considering, it seems promising to define the amount of information leaked to be H(l), and the remaining uncertainty to be H(h|l). n This seems to be the literature consensus: n n n Clarke, Hunt, Malacaria Köpf and Basin — also use G(l) and G(h|l) Clarkson, Myers, Schneider (? ) — Sec. 4. 4, when the attacker’s belief matches the a priori distribution 44

What about Step 2? n “ 2. Show that the notion gives appropriate security guarantees. ” n “Leakage = 0 iff noninterference holds” n Good, but this establishes only that the zero/nonzero distinction is meaningful! n More interesting is the Fano Inequality. n But this gives extremely weak bounds. n Does the value of H(h|l) accurately reflect the threat to h? 45

An Attack n Copy 1/10 of the bits of h into l. n l = h & 017777… 7; n Gives 2. 1 = n. 1 equivalence classes, each of size 2. 9 log n = n. 9. n H(l) =. 1 log n n H(h|l) =. 9 log n n After this attack, 9/10 of the bits are completely unknown. 46

Another Attack n Put 90% of the possible values of h into one big equivalence class, and put each of the remaining 10% into singleton classes: n if (h < n/10) l = h; else l = -1; n H(l) =. 9 log (1/. 9) +. 1 log n ≈. 1 log n +. 14 n H(h|l) =. 9 log (. 9 n) ≈. 9 log n –. 14 n Essentially the same as the previous attack! n But now O can guess h with probability 1/10. 47

A New Measure n With H(h|l), we can’t do Step 2 well! n Why not use Step 2 to guide Step 1? n Define V(h|l), the vulnerability of h given l, to be the probability that O can guess h correctly in one try, given l. 48

Calculating V(h|l) when h is uniformly distributed n As before, assume that n |S| = n and h is uniformly distributed n The partition has r equivalence classes C 1, C 2, …, Cr and |Ci| = ni r n V(h|l) = Σ (ni/n) (1/ni) = r/n i=1 n So all that matters is the number of equivalence classes, not their sizes! 49

Examples a. Noninterference case: r = 1, V(h|l) = 1/n b. Total leakage case: r = n, V(h|l) = 1 c. Copy 1/10 of bits: r = n. 1, V(h|l) = 1/n. 9 d. Put 1/10 of h’s values into singleton classes: r = 1 + n/10, V(h|l) ≈ 1/10 e. Put h’s values into classes, each of size 10: r = n/10, V(h|l) = 1/10 f. Password checker: r = 2, V(h|l) = 2/n 50

Conclusion n Maybe V(h|l) is a better foundation for quantitative information flow. n Using a single number is crude. n Compare examples d, e. n V(h|l) is not so good with respect to compositionality. 51