Advances in Logical Programming Environments Stuart Allen Richard

Advances in Logical Programming Environments Stuart Allen Richard Eaton Mark Bickford Christoph Kreitz Programming Logic Communications Secure software infrastructure Robert Constable Lorigo

Project goals Build open Logical Programming Environment - integrate programming language and logic share libraries of formalized mathematics enable cooperation among formal systems local reflection and code transformations Application to reliable embedded systems - semantics-based transformation and optimization - high-assurance software components and systems - formal component design

Progress • Nuprl LPE - new implementation with open architecture - formal documentation mechanisms - development of class theory - local reflection for weaving aspects • Application to networked systems - optimization of protocol stacks - compositional protocol verification - formal design of adaptive systems

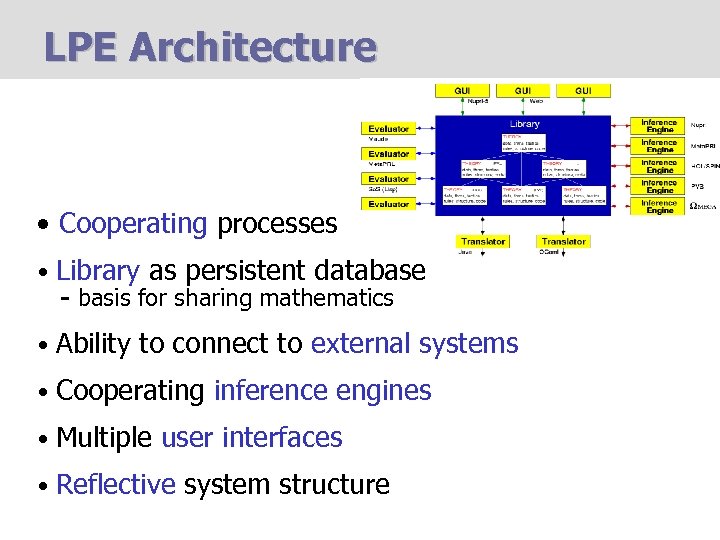LPE Architecture • Cooperating processes • Library as persistent database - basis for sharing mathematics • Ability to connect to external systems • Cooperating inference engines • Multiple user interfaces • Reflective system structure

Formal Documentation • Create documentation from formal objects - formal design expertise in “readable” form - screen display, La. Te. X articles, HTML documents • Comments contain references to objects - formal content browsable while reading text • Display objects determine term presentation - print representation (screen/La. Te. X macros) - suppressing formal parameters - preferences vs. parentheses

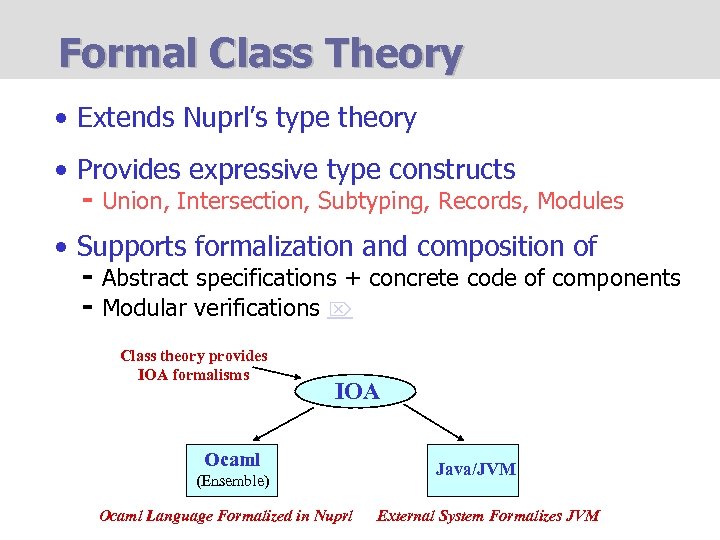Formal Class Theory • Extends Nuprl’s type theory • Provides expressive type constructs - Union, Intersection, Subtyping, Records, Modules • Supports formalization and composition of - Abstract specifications + concrete code of components - Modular verifications Class theory provides IOA formalisms IOA Ocaml (Ensemble) Ocaml Language Formalized in Nuprl Java/JVM External System Formalizes JVM

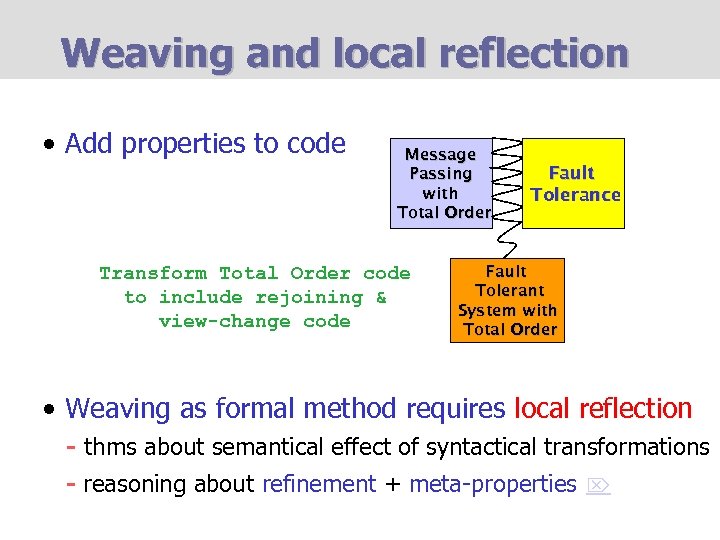Weaving and local reflection • Add properties to code Message Passing with Total Order Transform Total Order code to include rejoining & view-change code Fault Tolerance Fault Tolerant System with Total Order • Weaving as formal method requires local reflection - thms about semantical effect of syntactical transformations - reasoning about refinement + meta-properties

Formal Optimization • Optimize component-based network systems • generate fast-path for common case • compress message headers (demo available) • Automate with Nuprl LPE • Identify Common Case Predicates • Component code + CCP -> optimization theorem • System composition -> theorem composition • Composed theorem -> new system code Fast, abstract, verifiably correct results, speedup factor 3 -4

Compositional Protocol Verification Incremental through proof inheritance: • (A = P) (A B = P) A B intersects: • states, actions • initial states, transitions Total = total ETO = total view Induction: 1. A I = I 2. B I = I 3. A. init B. init I A B=I Total ETO View = view

Formal Design of Adaptive Systems Joint work with Robbert Van Renesse, Xiaoming Liu, Ken Birman • Adapt system to suit run-time dynamics - system upgrades - changing conditions (higher security levels, …) - use optimal implementations of components • Usually complicated • Building block approach - generic switching protocol switch spec constructs hybrid protocols from simpler ones - flexible, easy to prove correct spec

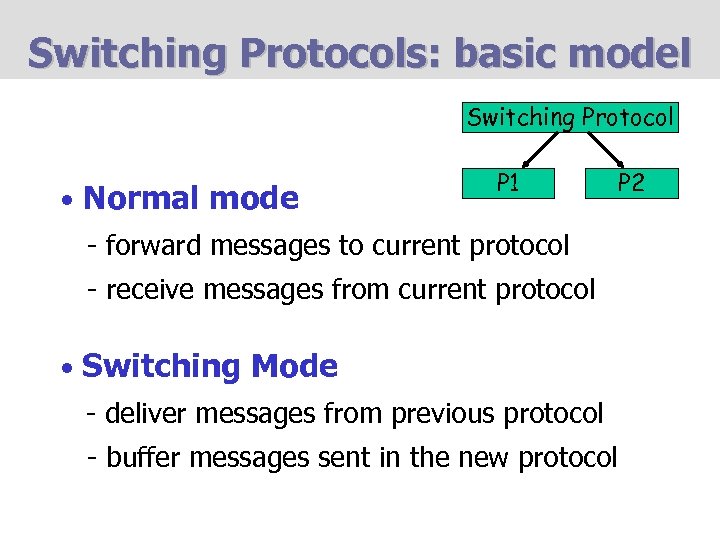Switching Protocols: basic model Switching Protocol • Normal mode P 1 - forward messages to current protocol - receive messages from current protocol • Switching Mode - deliver messages from previous protocol - buffer messages sent in the new protocol P 2

What kind of properties will be preserved by switching? Reliability? Integrity? Confidentiality? Prioritized Delivery? Total Order? Virtual Synchrony? In other words, what are the metaproperties of these properties ? Inject formal methods at earliest design stage

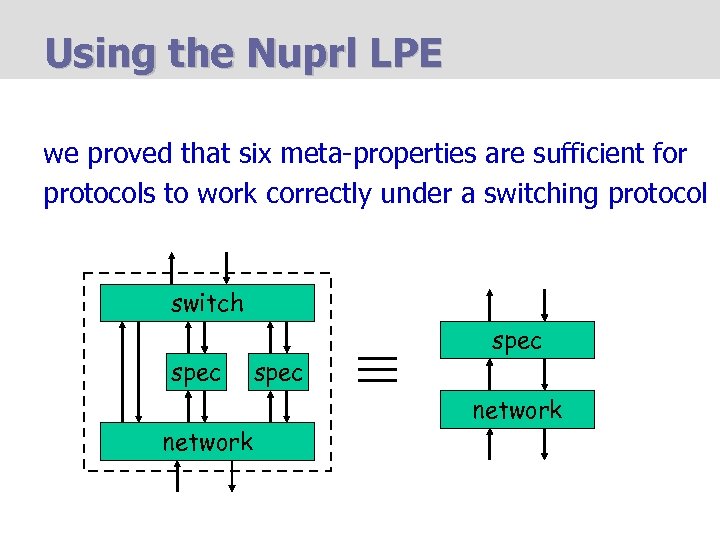Using the Nuprl LPE we proved that six meta-properties are sufficient for protocols to work correctly under a switching protocol switch spec network

Formal Model of Communication • Communication property - predicate P on traces • Trace - List tr of send and receive events Send(p, m) : message p sent by process m Deliver(p, m) : message p received by process m

Properties, formalized • Reliability p, m. Send(p, m) tr q. Deliver(q, m) tr • Integrity (T: set of trusted processes) q T. Deliver(q, m) tr p T. Send(p, m) tr • Confidentiality q T. Deliver(q, m) tr p T. Send(p, m) tr ) • Total order q 1, q 2, m 1, m 2. Deliver(q 1, m 1) tr Deliver(q 2, m 1) tr Deliver(q 1, m 2) tr Deliver(q 2, m 2) tr Deliver(q 1, m 1) < Deliver(q 1, m 2) Deliver(q 2, m 1) < Deliver(q 2, m 2)

Meta-property • Predicate M on properties of protocols • Expressed by relation R between traces tru, trl above and below a protocol layer M(P) tru, trl. P(trl) trl R tru P(tru) • Requires capability for higher order reasoning

Meta-properties for Switching Safety Asynchrony Delayable Send-enabled } Memoryless } Composable Layered Communication Protocol Switching RRasync(tr , tr ) ) ) = tr = [Send(p, trtr ) for ee, e 2 with ) )]… R swap-adjacent(trmsg(e) {m , tr , , m delay (tr , tr l u RRsend-e (tru u, trll)l)l 1, tr. Rsafety (trlu trtr=[] |interleave(tr 1 u, e 2 l 1 with(P) (tru , l 2 swap-adjacent(trll , mu 1), . . , Send(pntrln}] , tr tr trul 1 @ l) l - [etr … for 1 1, . . , m 2 n tr , tr 2 (P) 1, tr)u M composable u memoryless Switchable(P) process(e ) )process(e )composable ) Msafety e 1=Send(p, m 1 e 2 = Deliver(p, m 2 1 2

Verifying Hybrid Protocols Nuprl proof developed in parallel to implementation P. tru, trl. switch_invariant(tru, trl) Switchable(P) (P(pr 1(trl)) P(pr 2(trl))) P(tru) Switchable properties are preserved if the switch implementation satisfies a switch invariant • tru results from swapping trl events with different origin • messages sent by different protocols must be delivered in the same order Formal design at same pace as “informal” one

Lessons learned • The component-based approach is ideal for building adaptive systems • Employing formal techniques at every design stage is of great use for building efficient network systems • The LPE is capable of supporting “real” design - its theory is very expressive - reflection supports reasoning about program transformation • Automation still needs to be increased • More experience from applications is necessary

Plans • Design & verification of new programs - New hybrid protocols (adaptivity) - Probabilistic protocols (scalability) • Extend scope of automation - Domain-specific reasoning strategies - Connect external inference engines - Formalize design knowledge (e. g. as theorems) - Techniques for automated system (code) synthesis • Develop and deploy full reflection mechanism • Build formal infrastructure for practitioners - Include library of formally documented mathematics