Advanced Topics in Search Theory Pandora s Problem Based

Advanced Topics in Search Theory Pandora’s Problem Based on: “Optimal Search for the Best Alternative”, Econometrica, May 1979 by Marty Weitzman

In Today’s Class q Pandora’s problem formal presentation q Difference from “one-sided search” q Solution principle 2

Pandora’s Problem q There are n closed boxes q Box i, 1≤i≤n, contains a potential reward with comulative distribution function , independent of the other rewards q It costs to open box i and learn its contents, which becomes known after a time lag of q - representing a fallback reward that could always be collected (usually set to 0) q Originally, discount factor – r (but we’ll ignore that)

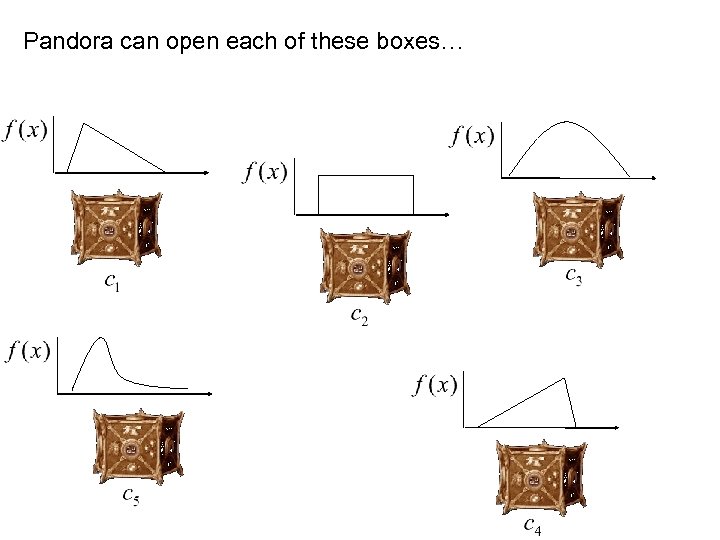
Pandora can open each of these boxes…

The Decision Problem q At each stage: – Decide whether or not to open a box – If stop – collect at that time the maximum reward – If continue: • Select next box to open • Pay the fee for opening • Wait for the outcome q Notice: the sum of search costs is paid during search whereas maximum reward is collected after the search has been terminated 5

The Goal q Find a sequential decision rule that will tell at each stage whether or not to continue searching, in if so, which box to open next, in a way that maximize the expected present discounted value 6

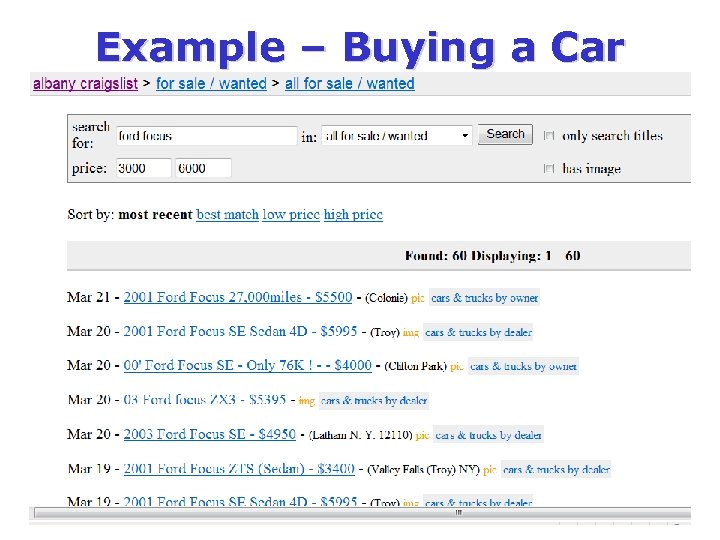
Example – Buying a Car

Each ad is a box… - With a distribution of utility Value of car -With a an opening fee Strategy: which car to see first, which second (and so on) and when to stop and buy?

Other Application q Oil drilling q Investing in new technology q Buying a new DVD: – Better chance for a good price at the outlet store (but higher cost to get there)

Dynamic-Programmingbased Solution q Let the collection of n boxes, denoted I, be partitioned into: – S – set of sampled boxes – - complementing set of closed boxes q We use y to represent the maximum sampled reward q It is enough to know y in order to make a decision (since the probability distributions are independent, once a box is opened its original distribution has no meaning any more) 10

q The state of the system is thus given by: q Define: - expected value of following the optimal policy onwards q At stage Pandora can: – Terminate search, collecting a reward y – Open box 11

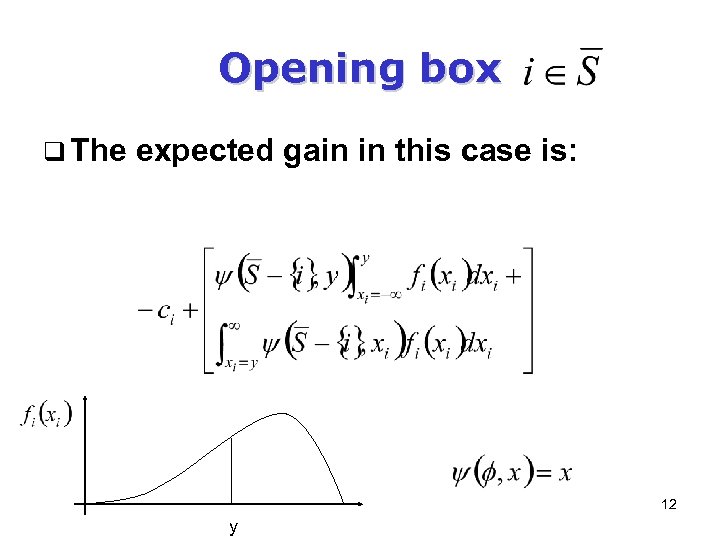
Opening box q The expected gain in this case is: 12 y

Dynamic Programming Now solve recursively for : -Solve for all cases where one box is closed -Then for two boxes -Then three and so on… Combinatoric task… 13

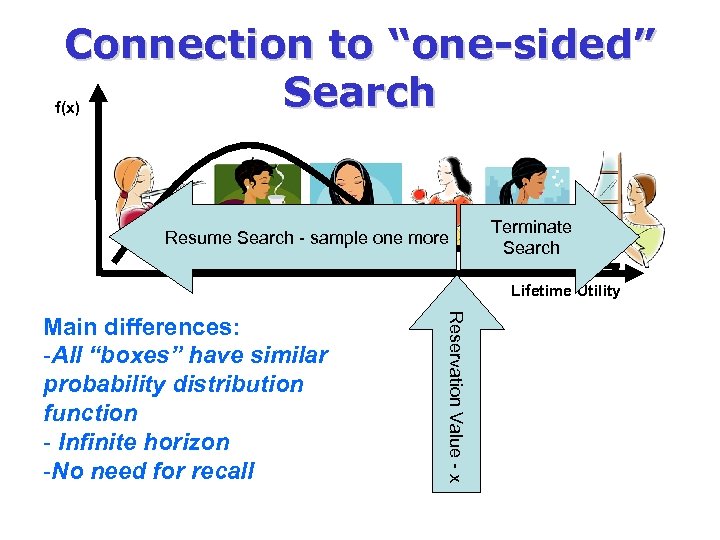
Connection to “one-sided” Search f(x) Resume Search - sample one more Terminate Search Lifetime Utility Reservation Value - x Main differences: -All “boxes” have similar probability distribution function - Infinite horizon -No need for recall

The optimal strategy q Suppose there are just 2 boxes: – One closed box i – Other is opened hypothetical box with reward q The decision: – Don’t open box i: receive – Open box, receive expected net benefit: 15

The optimal strategy q The indifference (or equivalence) between opening/not opening is when: 16

The Reservation Value q The value which satisfies the equation is called “reservation value” of box i: 17

The Optimal Strategy q Pandora’s Rule: – Selection Rule: if a box is to be opened, it should be that closed box with highest reservation price – Stopping Rule: Terminate search whenever the maximum sampled reward exceeds the reservation price of every closed box 18

Interesting Implications q Entire structure of the optimal policy has been reduced to a simple statement about reservation prices q The reservation value of each box is calculated by equating a hypothetical gain of stopping with the myopic gain of opening the box and terminating (rather than the full gain of opening the box and continuing on in an optimal manner) 19

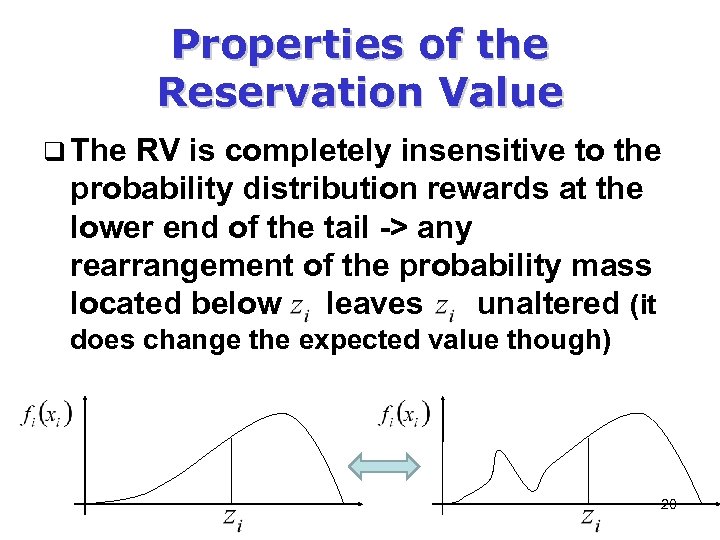
Properties of the Reservation Value q The RV is completely insensitive to the probability distribution rewards at the lower end of the tail -> any rearrangement of the probability mass located below leaves unaltered (it does change the expected value though) 20

Properties of the Reservation Value q Other things being equal, it is optimal to sample first from distributions which are more spread out or riskier q These low-probability high-payoff situations should be prime candidates for early investigation even though they have a smaller chance of ending up as the source ultimately yielding the maximum reward when the search ends

Properties of the Reservation Value q RV decreases with: – Greater search cost

Equivalent? Pandora already opened 4 boxes Pandora already opened 1 box Best prize found so far was 12

RV and Expected Benefit q It’s easy to find the optimal policy… q … but difficult to calculate the expected net benefit of that strategy 24

Expected Benefit Calculation terminating search on first trial terminating search after the i-th box Trying all boxes where:

Limitations of the model q Current assumptions do not consider: – Adaptive learning about correlated probability distributions – Parallel search – Risk aversion – Incomplete or no recall – Binding time horizon – Uncertain search costs or time –… 26

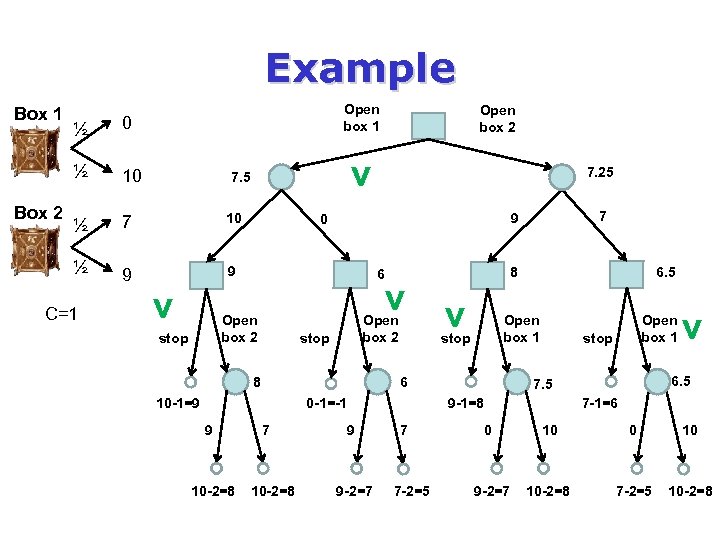
Example Box 1 Open box 1 0 ½ 10 ½ 7 10 ½ Box 2 ½ 9 9 C=1 v 7. 5 v 7. 25 6 v Open box 2 stop 8 10 -2=8 v 7 10 -2=8 6. 5 Open box 1 stop 0 -1=-1 9 8 6 10 -1=9 7 9 0 Open box 2 stop 9 -2=7 7 7 -2=5 0 9 -2=7 v 6. 5 7. 5 9 -1=8 9 Open box 1 7 -1=6 10 0 10 10 -2=8 7 -2=5 10 -2=8

פיתרון "פנדורה" לבעיה q חלופה 1 :

פיתרון "פנדורה" q חלופה 2: – 7> : Z בלתי אפשרי – 7=< : Z

Proof of Optimality q הוכחה באמצעות אינדוקציה על מספר הקופסאות הסגורות – נניח שכלל פנדורה אופטימלי עם m קופסאות סגורות וערך y הטוב ביותר שמצאנו עד כה – עבור 1= , m האופטימליות נובעת מעצם ההגדרה של ה- reservation value 03 – יש להוכיח כי כלל פנדורה הוא אופטימלי גם עבור 1+ m וערך y

הוכחה q נסתכל על הקופסה עם ה- rv הגבוה ביותר מבין 1+ m הקופסאות )נסמן את ה- rv שלה ב- (z q אם y>z הרי שאחרי שנפתח קופסה אחת נישאר עם m קופסאות שלפי האסטרטגיה האופטימלית לא כדאי לפתוח אף אחת מהן )הנחת האינדוקציה( – כלומר, השאלה היא אם כדאי לפתוח קופסה אחת בלבד 13 רווח מפתיחת הקופסה עלות פתיחת הקופסה

הוכחה )המשך( q אם : y<z – ברור שכדאי לפתוח לפחות קופסה אחת )אפילו אם נפתח רק את זו עם ה- RV הגבוה ביותר ואח"כ נעצור נקבל יותר מאשר אם לא נפתח כלל( – נניח שכדאי לפתוח תחילה קופסה אחרת, , k בעלת rv נמוך מ- z – אם נפתח אותה, נישאר עם m קופסאות אותן נפתח לפי כלל פנדורה )שאנחנו מניחים שהוא אופטימלי( 23

הוכחה )המשך( q אם : y<z – לחילופין, ניתן להסתכל על האלטרנטיבה הבאה: – אנו פותחים תחילה את הקופסה עם ה- rv הגבוה ביותר – אם מה שהתקבל בה גדול מה- rv השני הכי גבוה מסט הקופסאות אזי נעצור – אחרת, נפתח את הקופסה k – מנקודה זו נמשיך עם כלל פנדורה עם 1 - m קופסאות q המשך ההוכחה טכני – מראה שה- expected 33 payoff בחלופה האחרונה גבוה יותר

Problem 1 q You are about to purchase an i. Pod touch over the internet q You estimate the price distribution of the product over the different sellers to be uniform between 200 -300 dollars q You can search by yourself, by visiting different web-sites – the cost of time for obtaining a price quote is $1 q How will you search? What will be your expected cost? What’s the mean of the number of merchants you’ll visit?

Problem 2 q You decide not to wait and so you go to the mall in order to buy the i. Pod. q The mall’s parking lot charges you $8 per hour q There are 3 stores in the mall selling i. Pods: Store Distribution of Prices Time you’ll wait for service A U(80, 100) 20 min B U(70, 110) 10 min C Fixed - $80 1 hour q How will you conduct your search and what will be your overall expected cost?

Solution q This is actually Pandora’s Problem – The reservation value of Box i: – …and because we’re looking for minimum price:

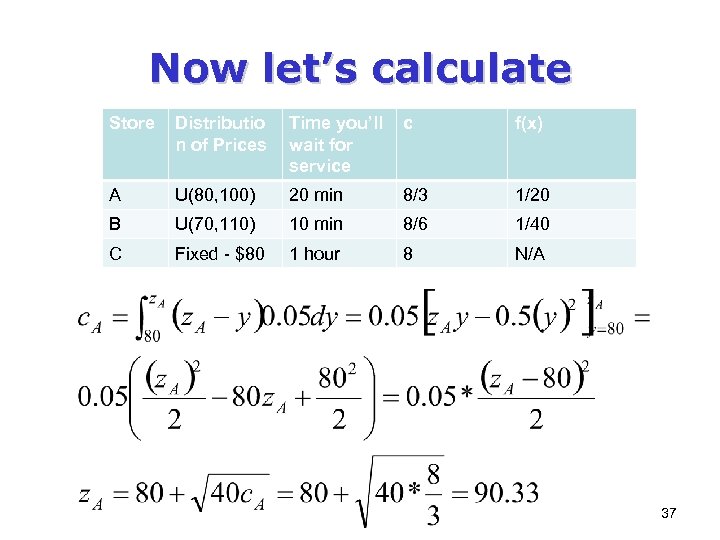
Now let’s calculate Store Distributio n of Prices Time you’ll wait for service c f(x) A U(80, 100) 20 min 8/3 1/20 B U(70, 110) 10 min 8/6 1/40 C Fixed - $80 1 hour 8 N/A 37

Similarly… q Optimal Strategy: – Sample B. If price below $88 then buy in store B. Otherwise, buy in store C.

Other Properties of Pandora q In many cases, the box we check first has the lowest chance of being the actual box used 39

הסתברות להגיע לקופסה q מה ההסתברות שנגיע לקופסה ? i … 5>-4>-3>-2>-1 ) P(reach i 04

הסתברות לעצור בקופסה i q מה ההסתברות שנגיע לקופסה i ובה נעצור? … 5>-4>-3>-2>-1 =)1+ P(stop at i)=P(reach i)-P(reach i 14

הסתברות שהפרס שלנו בסופו של דבר הוא מקופסה i q מה ההסתברות שנגיע לקופסה i ובסופו של דבר הערך שנמצא בה הוא הערך שנבחר? הסתברות שאם הערך בקופסה הוא x_i אז זה הערך שבו יבחר המחפש בסופו של דבר 24

מהי תוחלת מספר הקופסאות שנפתח? q תרגיל בית. 34

איך קופסה יכולה להשפיע על מצבה? q השפעה על ההסתברות שיגיעו אליה q השפעה על ההסתברות שהערך שלה ייבחר q השפעה על תוחלת "הערך המנוצל" שלה 44

השפעה על הסתברות ההגעה q באמצעות שינוי ה- cost משפיעים על ה- RV … 5>-4>-3>-2>-1 q הסתברות ההגעה החדשה לקופסה: q העלות c חסומה ב- 0 ולכן יש גבול לעליה ב- . RV לעיתים c שלילי ישים )למשל פרס אם תגיע 54 לחנות(

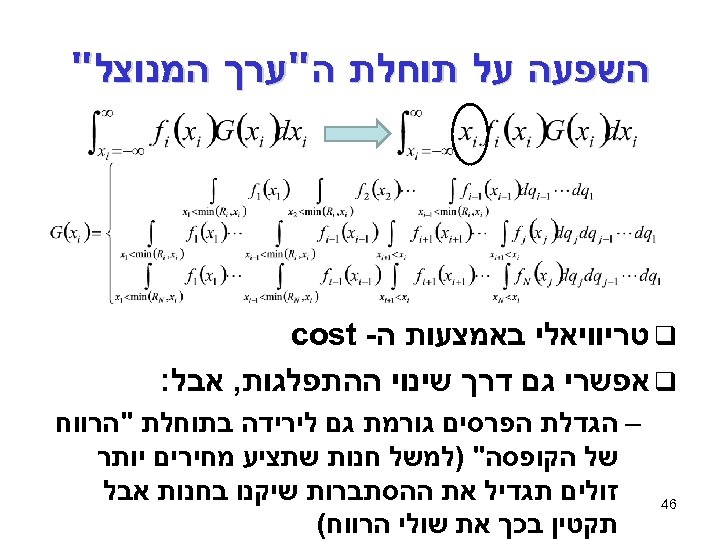
השפעה על תוחלת ה"ערך המנוצל" q טריוויאלי באמצעות ה- cost q אפשרי גם דרך שינוי ההתפלגות, אבל: 64 – הגדלת הפרסים גורמת גם לירידה בתוחלת "הרווח של הקופסה" )למשל חנות שתציע מחירים יותר זולים תגדיל את ההסתברות שיקנו בחנות אבל תקטין בכך את שולי הרווח(

טיפול ב- subsets q מה קורה כשמותר לנו לפתוח רק חלק מהקופסאות? למשל רק k מתוך ? N q תרגיל בית. 74

יכולת השפעה על מחפשים q מחפש שאיננו משתמש באסטרטגיית החיפוש האופטימלי – ביצועים ירודים q אסטרטגייה אפשרית – "מניפולציה" לבעיית החיפוש על-מנת "לדחוף" לאסטרטגיה אופטימלית עבור הבעיה המקורית 84

אוהבי תוחלת אסטרטגיה: q סידור הקופסאות לפי התוחלת + מחיר פתיחה q כלל עצירה: כאשר התוחלת+מחיר פתיחה של הקופסה הבאה שמועמדת לפתיחה גדול מערך אמיתי של קופסה שכבר פתחנו

אוהבי תוחלת המשך. . . q מניפולציה: כיוון שסדר החיפוש האופטימאלי ידוע והאסטרטגיה של אוהבי התוחלת ידועה אפשר לעשות על סט הקופסאות מניפולציה שתגרום למחפשים הנ"ל לחפש בדיוק כמו האופטימאלי. q עבור כל קופסה נשנה את פונקצית ההתפלגות שלה כך שהתוחלת החדשה של פונקצית ההתפלגות + מחיר הפתיחה יהיה שווה לערך הסף של אותה קופסה כפי שחושב עפ"י החיפוש האופטימאלי

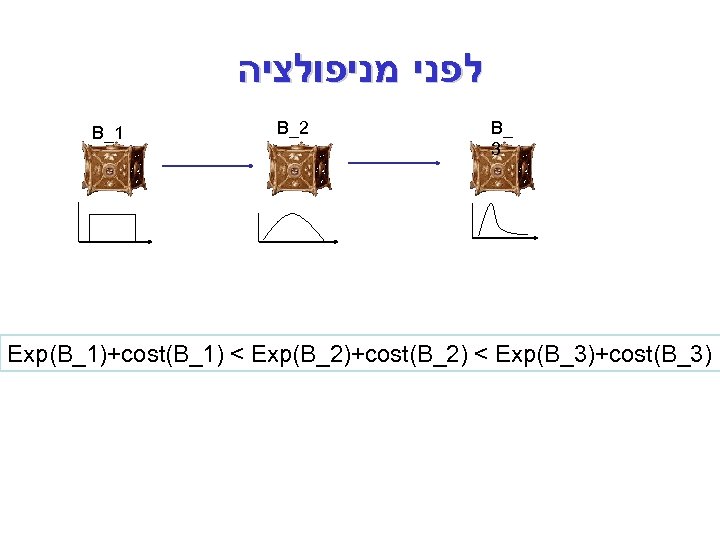
לפני מניפולציה B_1 B_2 B_ 3 Exp(B_1)+cost(B_1) < Exp(B_2)+cost(B_2) < Exp(B_3)+cost(B_3)

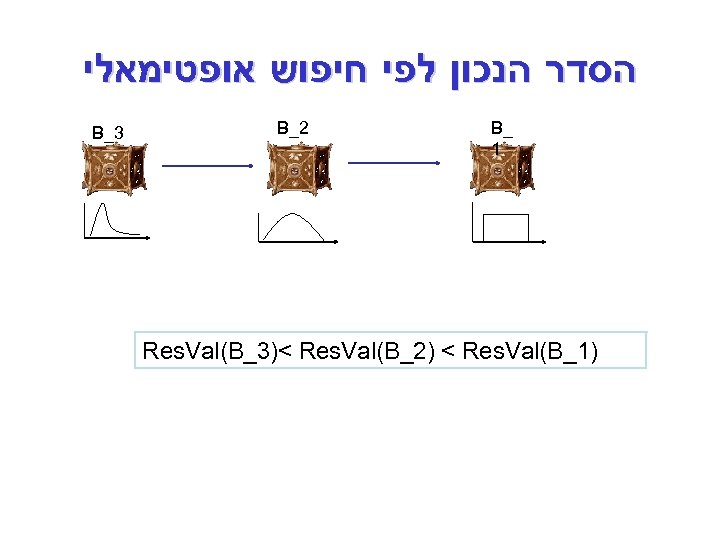
הסדר הנכון לפי חיפוש אופטימאלי _ B 1 2_ B )1_ Res. Val(B_3)< Res. Val(B_2) < Res. Val(B 3_ B

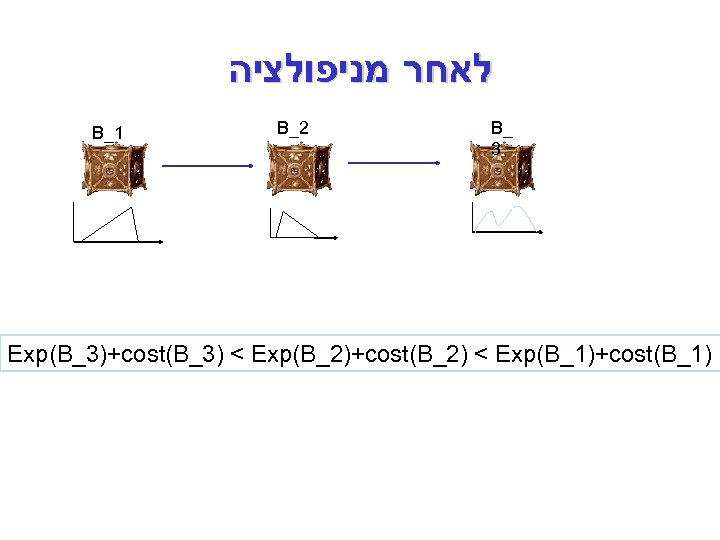
לאחר מניפולציה B_1 B_2 B_ 3 Exp(B_3)+cost(B_3) < Exp(B_2)+cost(B_2) < Exp(B_1)+cost(B_1)

ממעיטי החיפוש אסטרטגיה: q בחירה רנדומית של קופסה, לקיחת הערך שיש באותה קופסה רנדומית

ממעיטי החיפוש המשך מניפולציה: q חישוב תוחלת + מחיר פתיחה עבור כל קופסה. q נציג בפני המחפש אך ורק את הקופסה עם הערך הכי נמוך שחושב לעיל

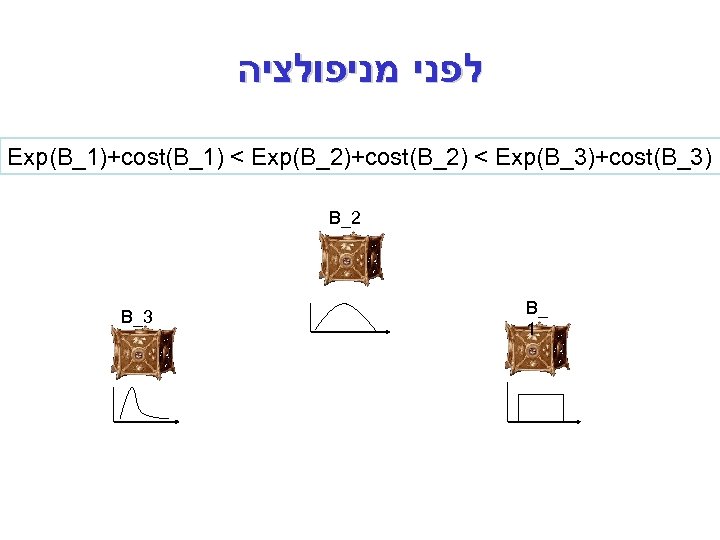
לפני מניפולציה Exp(B_1)+cost(B_1) < Exp(B_2)+cost(B_2) < Exp(B_3)+cost(B_3) B_2 B_3 B_ 1

לאחר מניפולציה הבעיה שמוצגת למשתמש: 1_ B

מרבי החיפוש אסטרטגיה: q מתשאלים כמעט כל קופסה כדי לקבל החלטה

מרבי החיפוש המשך מניפולציה: q לא נציג בפניהם את הקופסאות שהסיכוי שהמחפש האופטימאלי יתשאל אותן קטן. q לכל קופסה נחשב את ערך הסף ונחשב מה ההסתברות שנגיע לאותה קופסה לפי החיפוש האופטימאלי. אם ערך זה קטן מ alpha שקבענו אז לא נציג לפני המחפש את הקופסה הזו.

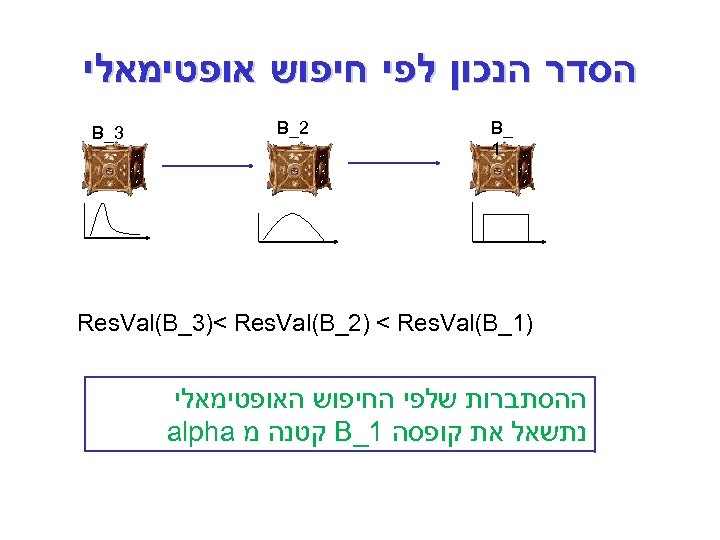
הסדר הנכון לפי חיפוש אופטימאלי _ B 1 2_ B 3_ B )1_ Res. Val(B_3)< Res. Val(B_2) < Res. Val(B ההסתברות שלפי החיפוש האופטימאלי נתשאל את קופסה 1_ B קטנה מ alpha

לאחר מניפולציה 2_ B 3_ B