Скачать презентацию Advanced Topics in Data Mining Sequential Patterns
f9219563b4d441532c98093e53495a13.ppt
- Количество слайдов: 70
Advanced Topics in Data Mining: Sequential Patterns
Sequential Pattern Analysis
Sequential Pattern Mining • Progress in bar-code technology has made it possible for retail organizations to collect and store massive amounts of sales data, referred to as the basket data • A record in such data typically consists of the transaction date and the items bought in the transaction • Very often, data records also contain customer-id, particularly when the purchase has been made using a credit card or a frequent-buyer card • Catalog companies also collect such data using the orders they receive
Sequential Pattern Mining • An example of such a pattern is that customers typically rent “Star Wars (星際大戰 )”, then “Empire Strikes Back (帝國大反擊 )”, and then “Return of the Jedi (絕地大反攻 )” • These rentals need not be consecutive – Customers who rent some other videos in between also support this sequential pattern • Elements of a sequential pattern need not be simple items – “Computer Science and Programming Language”, followed by “Data Structure”, followed by “System Programs and Operating Systems” is an example of a sequential pattern in which the elements are sets of items
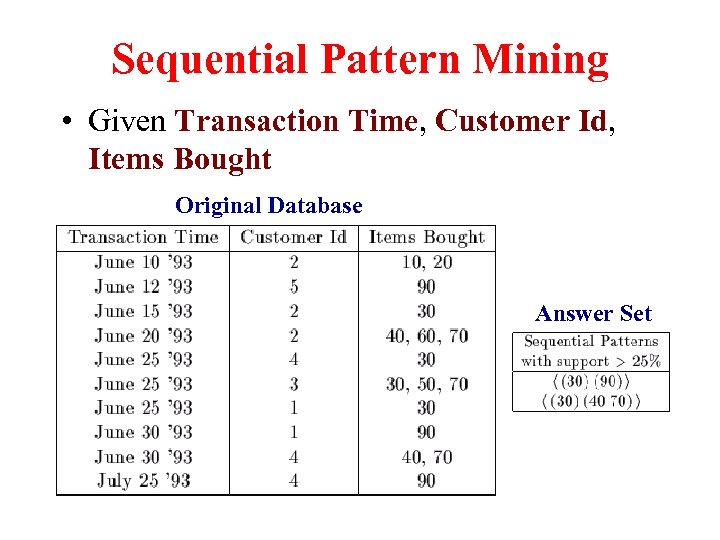Sequential Pattern Mining • Given Transaction Time, Customer Id, Items Bought Original Database Answer Set
Definition • The length of a sequence is the number of itemsets in the sequence • A sequence of length k is called a k-sequence • The support for an itemset i is defined as the fraction of customers who bought the items in i in a single transaction • The itemset i and the 1 -sequence have the same support • An itemset with minimum support is called a large (frequent) itemset or litemset
Apriori. All Algorithm • Each itemset in a large sequence must have minimum support • Any large sequence must be a list of litemsets • Finding all sequential patterns in five phases – Sort Phase – Litemset Phase – Transformation Phase – Sequence Phase – Maximal Phase
Apriori. All Algorithm: Sort Phase Customer-Sequence Version of the Database
Apriori. All Algorithm: Litemset Phase min_sup_count=2 Apriori/DHP FP Growth
Apriori. All Algorithm: Transformation Phase
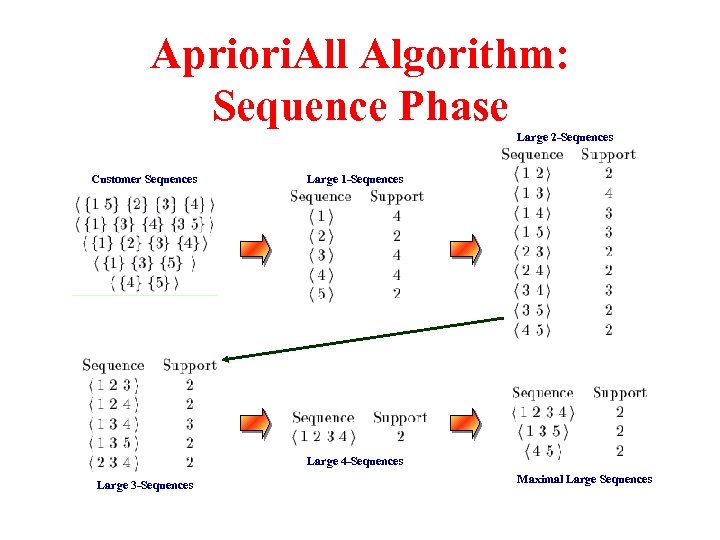Apriori. All Algorithm: Sequence Phase Large 2 -Sequences Customer Sequences Large 1 -Sequences Large 4 -Sequences Large 3 -Sequences Maximal Large Sequences
Sequence Phase: Candidate Generation
Apriori. All Algorithm: Maximal Phase • The sequence <(3) (4 5) (8)> is contained in <(7) (3 8) (9) (4 5 6) (8)>, since (3) (3 8), (4 5) (4 5 6) and (8) • The sequence <(3) (5)> is not contained in <(3 5)> (and vice versa) – The former represents items 3 and 5 being bought one after the other – The latter represents items 3 and 5 being bought together. • In a set of sequences, a sequence s is maximal if s is not contained in any other sequence.
Apriori. All Algorithm Answer Set • With minimum support set to 25%, i. e. , a minimum support of 2 customers – < (30) (90)> and <(30) (40 70)> are maximal – <(10 20) (30)> which is only supported by customer 2 does not have minimum support – <(30)>, <(40)>, <(70)>, <(90)>, <(30) (40)>, <(30) (70)> and <(40 70)>, though having minimum support, are not in the answer because they are not maximal.
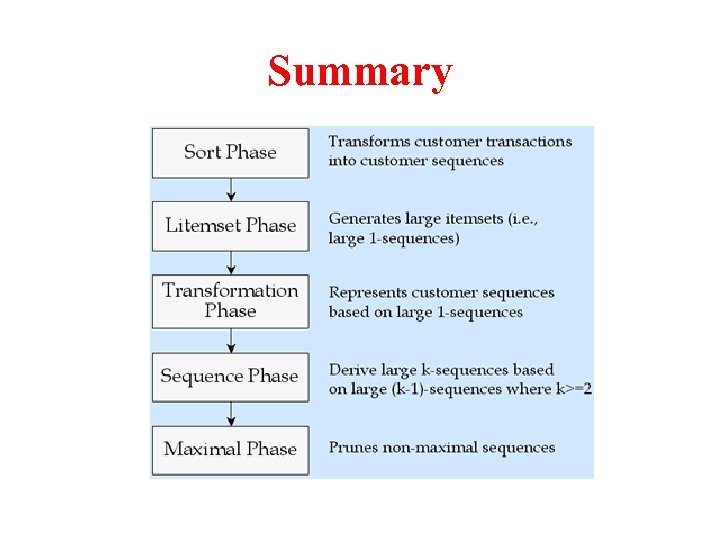Summary
Discussions • Apriori. All algorithm will generate a huge set of candidate sequences – If there are 1000 frequent sequences of length-1, the algorithm will generate 1000 × 1000 + (1000 × 999) / 2 = 1, 499, 500 candidate sequences • Many scans of databases in mining • Difficulties at mining long sequential patterns
Methods to Improve Apriori. All’s Efficiency • Prefix. Span – Without Candidate Generation – Reduce Database Scan (Scan Database Twice) & Database Size – The general idea of the method is to use projected sequence databases to confine the search and the growth of subsequence fragments
Prefix. Span • Prefix. Span-1 – Single-Level Projection • Prefix. Span-2 – Bi-Level Projection – S-Matrix • Prefix. Span use Pseudo-Projection
Definition A sequence : < (ef) (ab) (df) c b > A Sequence Database SID Sequence 10 20 30 40
Definition • Prefix and Postfix (Projection) – ,
Prefix. Span-1 • Find Length-1 (L 1) Sequential Patterns • Construct Projected Database According to L 1 • Mining Each Projected DB Recursively
Prefix. Span-1: An Example Sequence_ID Sequence 10 < a ( abc ) ( ac ) d ( cf ) > 20 < ( ad ) c ( bc ) ( ae ) > 30 40 < ( ef ) ( ab ) ( df ) cb > < eg ( af ) cbc > Min_Support_Count = 2 L 1: : 4, : 4,
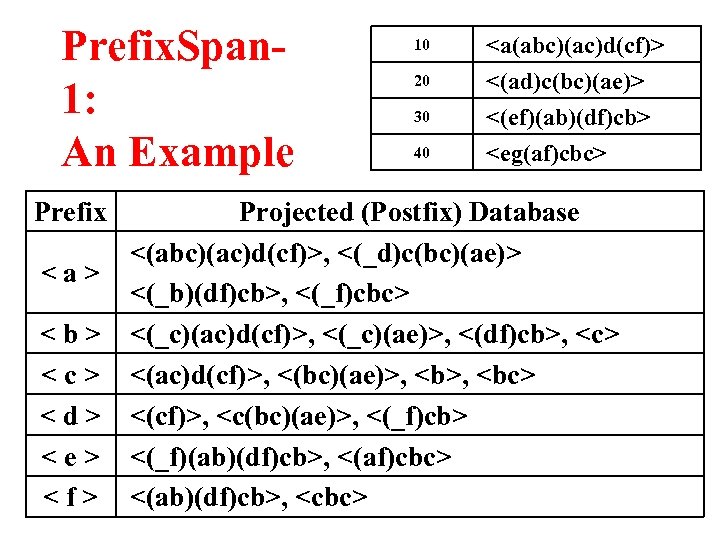Prefix. Span 1: An Example Prefix
Prefix. Span-1: An Example <(abc)(ac)d(cf)>, <(_d)c(bc)(ae)> <(_b)(df)cb>, <(_f)cbc> Scanning -Projected database once: a: 2, b: 4, c: 4, d: 2, e: 1, f: 2 (_b): 2, (_c): 1, (_d): 1, (_e): 1, (_f): 1 L 2:
Prefix. Span-1: An Example Prefix < aa > < ab > < (ab) > < ac > < ad > < af > Projected (Postfix) Database <(_bc)(ac)d(cf)> <(_c)(ac)d(cf)>, <(_c)a>,
Prefix. Span-1: An Example < ab > <(_c)(ac)d(cf)>, <(_c)a>,
Prefix. Span-1: An Example Prefix < a(bc) > < aba > < abc > Projected (Postfix) Database <(ac)d(cf)> , <(_c)d(cf)>
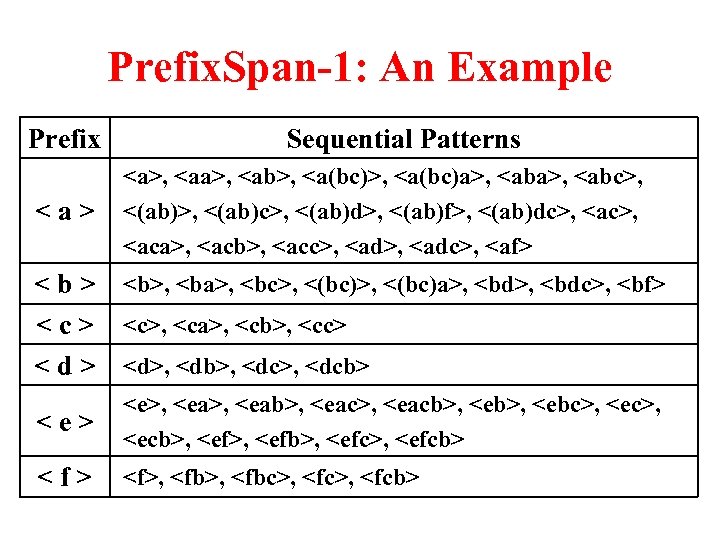Prefix. Span-1: An Example Prefix Sequential Patterns ,
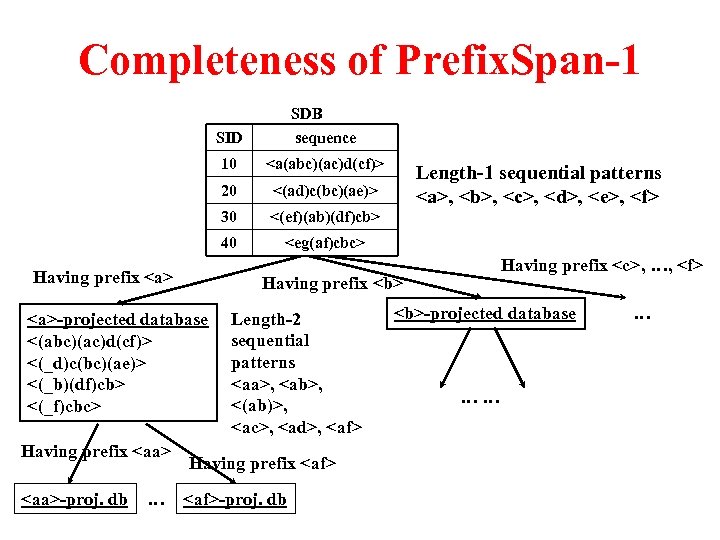Completeness of Prefix. Span-1 SID 10
Analysis • No candidate sequence needs to be generated by Prefix. Span • Projected databases keep shrinking • The major cost of Prefix. Span is the construction of projected databases
Prefix. Span-2 • Find Length-1 Sequential Patterns • Construct Triangular Matrix M (S-Matrix) – By scanning DB second time, the S-matrix can be filled up • Construct Projected Database – For each length-2 sequential pattern, construct its projected DB • Mining each projected DB recursively
Prefix. Span-2: An Example Sequence_ID Sequence 10 < a ( abc ) ( ac ) d ( cf ) > 20 < ( ad ) c ( bc ) ( ae ) > 30 40 < ( ef ) ( ab ) ( df ) cb > < eg ( af ) cbc > Min_Support = 2 L 1: : 4, : 4 ,
Prefix. Span-2: An Example
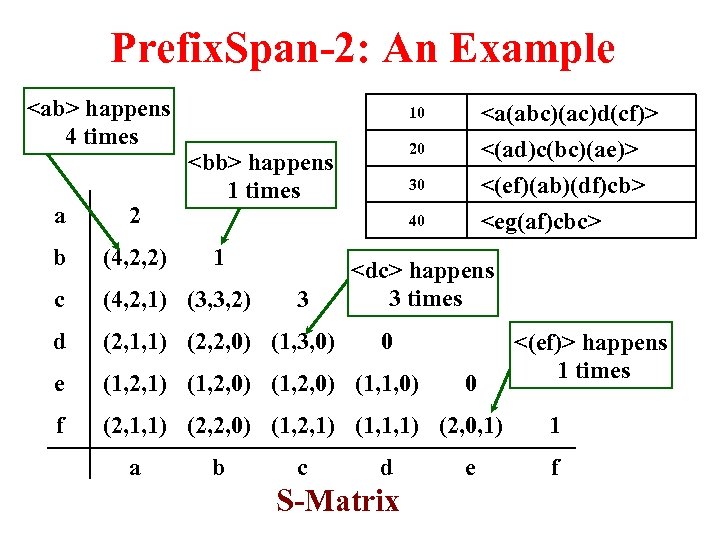Prefix. Span-2: An Example a 2 b (4, 2, 2) 1 c (4, 2, 1) (3, 3, 2) 3 d (2, 1, 1) (2, 2, 0) (1, 3, 0) 0 e (1, 2, 1) (1, 2, 0) (1, 1, 0) 0 f (2, 1, 1) (2, 2, 0) (1, 2, 1) (1, 1, 1) (2, 0, 1) a b c d e 10
Benefits of Bi-Level Projection • More patterns are found in each shoot • Much Less Projections – In this example, there are 53 patterns • 53 Level-by-Level Projections • 22 Bi-Level Projections
Speed-Up by Pseudo-Projection • Major Cost of Prefix. Span: Projection – Postfixes of sequences often appear repeatedly in recursive projected databases • When (projected) database can be held in main memory, use pointers to form projections – Pointer to the sequence – Offset of the postfix s|: ( , 2) s=
Mining Time-Gap Sequential Patterns (TGSP) • Sequential Pattern –A B C • Time Gap Sequential Pattern –A B C (3 -5) (5 -7)
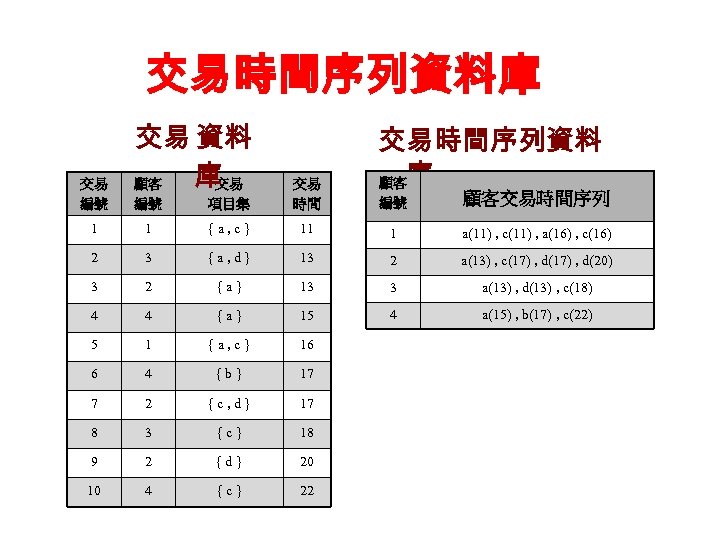交易時間序列資料庫 交易 編號 交易 資料 庫 顧客 交易 編號 項目集 交易 時間 1 1 {a, c} 2 3 3 交易時間序列資料 顧客庫 編號 顧客交易時間序列 11 1 a(11) , c(11) , a(16) , c(16) {a, d} 13 2 a(13) , c(17) , d(20) 2 {a} 13 3 a(13) , d(13) , c(18) 4 4 {a} 15 4 a(15) , b(17) , c(22) 5 1 {a, c} 16 6 4 {b} 17 7 2 {c, d} 17 8 3 {c} 18 9 2 {d} 20 10 4 {c} 22
交易時間序列 • K-交易時間序列 – < I 1(T 1), I 2(T 2), …, Ik(Tk)> – 顧客 1存在 3 -交易時間序列
交易時間間隔 &項目序列 • K-交易時間間隔序列 – 表示成＜ I 1, (t 1), I 2, (t 2), …, (tk-1), Ik＞ 其中 Ii為單一項目， ti為 Ii與 Ii+1購買時間間隔 – 3 -交易時間序列 ＜ A(10), B(15), D(30)＞ 的交易時 間間隔序列為 ＜ A, (5), B, (15), D＞ • K-項目序列 – 表示成 ，為多個項目依照購買時間 先後排列而成的，若其相同時間購買之項目，則 以編號較小之項目排在前面 • 3 -交易時間序列 < A(10), B(15), D(30)>所對應 的 3 -項目序列為
時間間隔序列 & 包含 • K-時間間隔序列 – 表示成＜ I 1， 1， 2， 2， Rk-1， k＞ ， R I R …， I 其中 Ii為一個單 一項目，Ri = li ~ ui，為一段時間範圍，表示項目 Ii與 Ii+1的購買時間間隔範圍介於 li和 ui中間 • 4 -時間間隔序列 – ＜ A, (5~8), B, (3~6), C, (5~8), D＞ • 交易時間間隔序列＜ A, (7), B, (4), C, (5), D＞ 包 含 於時間間隔序列＜ A, (5~8), B, (3~6), C, (5~8), D＞
支持 • 顧客交易時間序列 C =＜ A(15), B(22), C(26), D(31), E(39)＞ 存在一個 4 -交易時間序列 ＜ A(15), B(22), C(26), D(31)＞ 此交易時間序列的交易時間間隔序列為 ＜ A, (7), B, (4), C, (5), D＞ 包含於時間間隔序列 S =＜ A, (5~8), B, (3~6), C, (5~8), D＞ 所以顧客交易時間序列 C支持時間間隔序 列 S ，且此顧客交易時間序列 C支持項目 序列
支持度 • K-時間間隔序列 的 支持度 為支持此時間間 隔序列的顧客數與資料庫中所有顧客數的 比值 • 若 K-時間間隔序列的支持度大於或等於使 用者所訂定的 最小支持度 的話，我們將其 稱為 K-頻繁時間間隔序列 • K-項目序列 的 支持度 為支持此項目序列的 顧客數與資料庫中所有顧客數的比值 • 若 K-項目序列的支持度大於或等於 最小支 持度 ，則我們稱之為 K-頻繁項目序列
挖掘時間間隔序列型樣 找出 1 -頻繁項目序列 找出 2 -頻繁項目序列 產生 2 -項目序列資料庫 找出 2 -頻繁時間間隔序列 產生 K-項目序列資料庫 (K≧ 3) 找出 K-頻繁時間間隔序列 (K≧ 3) • 找出時間間隔序列型樣 • • •
找出 1 -頻繁項目序列 ID 顧客交易時間序列 1 A(5) B(10) C(19) D(27) E(32) 假設 最小支持度 為 1/2 2 A(8) B(13)F(13) C(23) D(31) 各項目支持度為 3 A(9) B(14) C(23) D(31) 4 A(13) B(19) C(29) D(37) 5 A(15) B(21) F(21) D(28) A(36) 6 C(16) A(21) B(26) F(26) D(31) 7 E(18) C(27) A(34) B(40) F(40) 8 A(18) B(24) F(24) C(27) E(33) A=8/8=1, B=8/8=1, C=7/8, D=6/8, E=3/8, F=5/8， 則 項目 A， C， F為 1 B， D， 頻繁項目序列
找出 2 -頻繁項目序列 • 產生 2 -候選項目序列 – 由 1 -頻繁項目序列 A， C， F 配對後可以產生＜ AA＞ , B， D， ＜ AB＞ , ＜ AC＞ , ＜ AD＞ , ＜ AF＞ , ＜ BA＞ , ＜ BB＞ , ＜ BC＞ , ＜ BD＞ , ＜ BF＞ , ＜ CA＞ , ＜ CB＞ , ＜ CC＞ , ＜ CD ＞ , ＜ CF＞ , ＜ FA＞ , ＜ FB＞ , ＜ FC＞ , ＜ FD＞ , ＜ FF＞ 的 2 -候選項目序列 • 產生 2 -頻繁項目序列 – 掃描資料庫，計算 各 2 -候選項目序列 的支持度 • ＜AA＞=1/8, ＜AB＞=1, ＜AC＞=5/8, ＜AD＞=6/8, ＜AF＞=5/8, ＜BA＞=1/8, ＜BB＞=0, ＜BC＞=5/8, ＜BD＞=6/8, ＜BF＞=5/8, ＜CA＞=2/8, ＜CB＞=2/8, ＜CC＞=0, ＜CD＞=5/8, ＜CF＞=2/8, ＜FA＞=1/8, ＜FB＞=0, ＜FC＞=2/8, ＜FD＞=3/8, ＜FF＞=0 – 產生 2 -頻繁項目序列 (1/2) • ＜ AB＞ , ＜ AC＞ , ＜ AD＞ , ＜ AF＞ , ＜ BC＞ , ＜ BD＞ , ＜ BF ＞, ＜ CD＞ 為 2 -頻繁項目序列
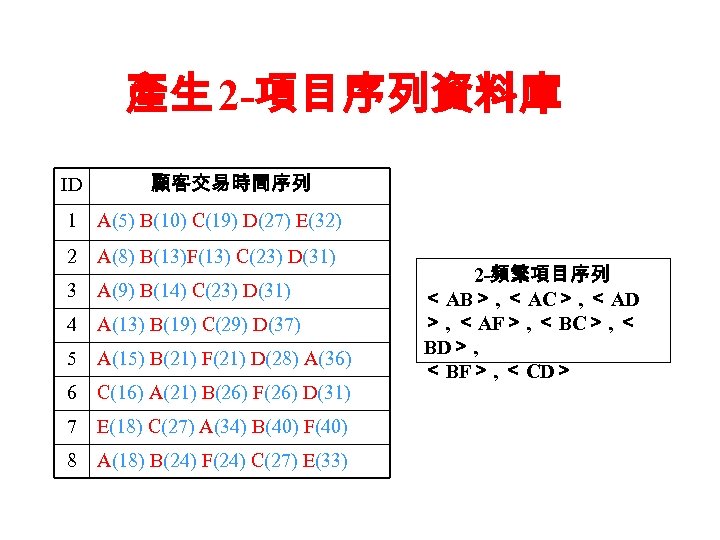產生 2 -項目序列資料庫 ID 顧客交易時間序列 1 A(5) B(10) C(19) D(27) E(32) 2 A(8) B(13)F(13) C(23) D(31) 3 A(9) B(14) C(23) D(31) 4 A(13) B(19) C(29) D(37) 5 A(15) B(21) F(21) D(28) A(36) 6 C(16) A(21) B(26) F(26) D(31) 7 E(18) C(27) A(34) B(40) F(40) 8 A(18) B(24) F(24) C(27) E(33) 2 -頻繁項目序列 ＜ AB＞ , ＜ AC＞ , ＜ AD ＞ , ＜ AF＞ , ＜ BC＞ , ＜ BD＞ , ＜ BF＞ , ＜ CD＞
產生 2 -項目序列資料庫 ID 顧客交易時間序列 1 A(5) C(10) B(13) A(15) C(20) 2 A(8) B(13) C(23) D(31) 在產生 2 -項目序列資料庫時，顧客 1會拆解 出 { A(5) C(10) }、{ A(5) B(13) }、{ A(5) A(15) }、{ C(10) B(13) }、{ C(10) A(15) }、{ C(10) C(20) }、{ B(13) A(15) } 、 B(13) C(20) }、{ A(15) C(20) } { { A(5) C(20) } 則不產生。
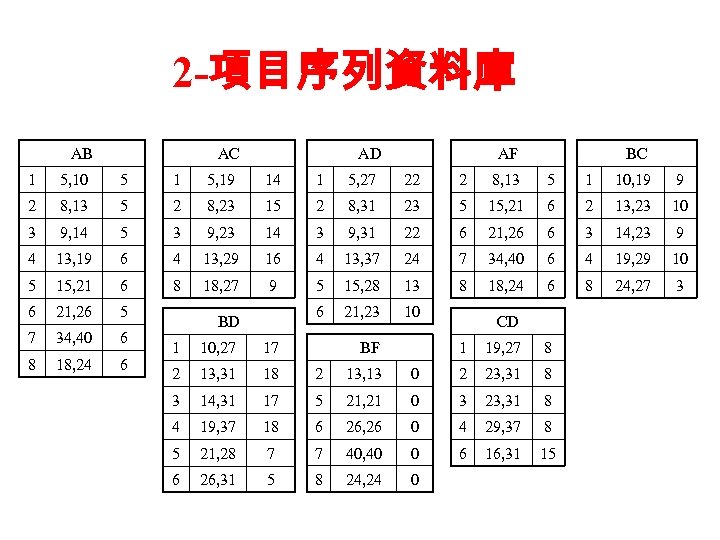2 -項目序列資料庫 AB AC AD AF BC 1 5, 10 5 1 5, 19 14 1 5, 27 22 2 8, 13 5 1 10, 19 9 2 8, 13 5 2 8, 23 15 2 8, 31 23 5 15, 21 6 2 13, 23 10 3 9, 14 5 3 9, 23 14 3 9, 31 22 6 21, 26 6 3 14, 23 9 4 13, 19 6 4 13, 29 16 4 13, 37 24 7 34, 40 6 4 19, 29 10 5 15, 21 6 8 18, 27 9 5 15, 28 13 8 18, 24 6 8 24, 27 3 6 21, 26 5 6 21, 23 10 7 34, 40 6 8 18, 24 6 BD BF 1 10, 27 17 2 13, 31 18 2 13, 13 3 14, 31 17 5 4 19, 37 18 5 21, 28 6 26, 31 CD 1 19, 27 8 0 2 23, 31 8 21, 21 0 3 23, 31 8 6 26, 26 0 4 29, 37 8 7 7 40, 40 0 6 16, 31 15 5 8 24, 24 0
找出 2 -頻繁時間間隔序列 最小密度： 5 (個 ) 最小支持度： 15 (個 ) 單元長度： 1 輸出頻繁時間間隔序 列A B [1, 3] 1. 若項目序列 AB資料列表沒有產生任何頻繁時間間隔序 列， 則刪除項目序列 AB的資料列表 2. 刪減項目序列 AB資料列表中投影點不在 u 1的資料
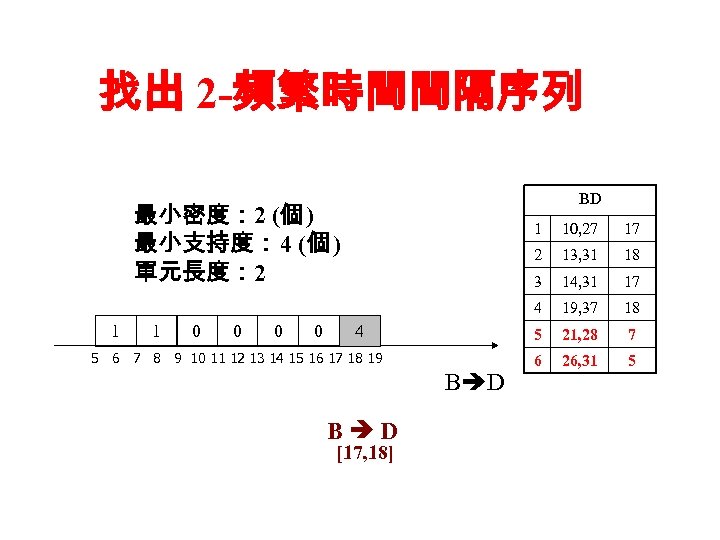找出 2 -頻繁時間間隔序列 BD 最小密度： 2 (個 ) 最小支持度： 4 (個 ) 單元長度： 2 1 0 0 B D [17, 18] 18 14, 31 17 19, 37 18 5 B D 13, 31 3 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 17 2 4 10, 27 4 1 1 21, 28 7 6 26, 31 5
![2 -頻繁時間間隔序列 A B A C A D B F C D [5, 6]](https://present5.com/presentation/f9219563b4d441532c98093e53495a13/image-52.jpg "2 -頻繁時間間隔序列 A B A C A D B F C D [5, 6]")
2 -頻繁時間間隔序列 A B A C A D B F C D [5, 6] [17, 18] [13, 16] [ 0, 0 ] [21, 24] [7, 8] A F [5, 6] B C [9, 10]
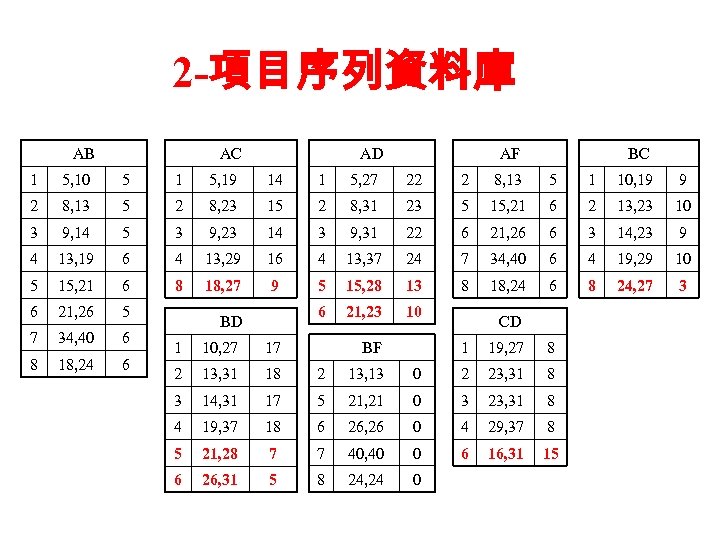2 -項目序列資料庫 AB AC AD AF BC 1 5, 10 5 1 5, 19 14 1 5, 27 22 2 8, 13 5 1 10, 19 9 2 8, 13 5 2 8, 23 15 2 8, 31 23 5 15, 21 6 2 13, 23 10 3 9, 14 5 3 9, 23 14 3 9, 31 22 6 21, 26 6 3 14, 23 9 4 13, 19 6 4 13, 29 16 4 13, 37 24 7 34, 40 6 4 19, 29 10 5 15, 21 6 8 18, 27 9 5 15, 28 13 8 18, 24 6 8 24, 27 3 6 21, 26 5 6 21, 23 10 7 34, 40 6 8 18, 24 6 BD BF 1 10, 27 17 2 13, 31 18 2 13, 13 3 14, 31 17 5 4 19, 37 18 5 21, 28 6 26, 31 CD 1 19, 27 8 0 2 23, 31 8 21, 21 0 3 23, 31 8 6 26, 26 0 4 29, 37 8 7 7 40, 40 0 6 16, 31 15 5 8 24, 24 0
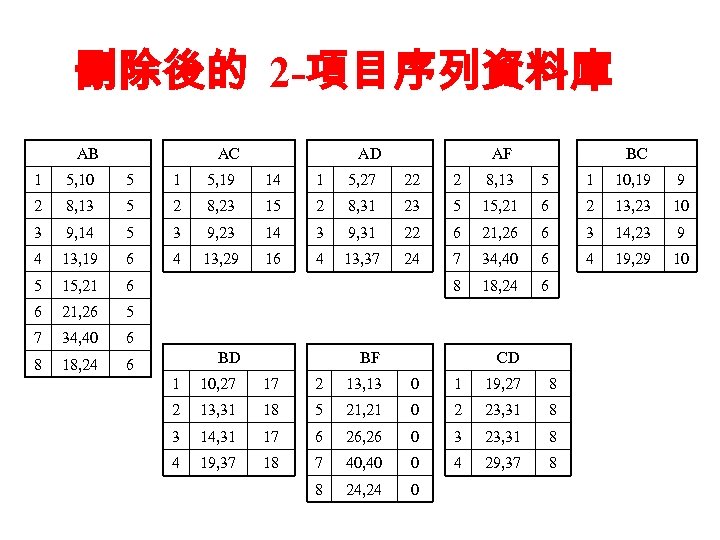刪除後的 2 -項目序列資料庫 AB AC AD AF BC 1 5, 10 5 1 5, 19 14 1 5, 27 22 2 8, 13 5 1 10, 19 9 2 8, 13 5 2 8, 23 15 2 8, 31 23 5 15, 21 6 2 13, 23 10 3 9, 14 5 3 9, 23 14 3 9, 31 22 6 21, 26 6 3 14, 23 9 4 13, 19 6 4 13, 29 16 4 13, 37 24 7 34, 40 6 4 19, 29 10 5 15, 21 6 8 18, 24 6 6 21, 26 5 7 34, 40 6 8 18, 24 6 BD BF CD 1 10, 27 17 2 13, 13 0 1 19, 27 8 2 13, 31 18 5 21, 21 0 2 23, 31 8 3 14, 31 17 6 26, 26 0 3 23, 31 8 4 19, 37 18 7 40, 40 0 4 29, 37 8 8 24, 24 0
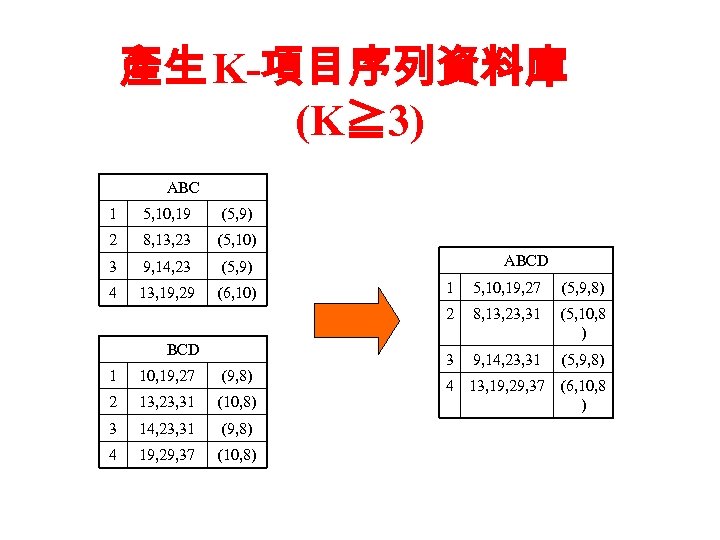產生 K-項目序列資料庫 (K≧ 3) ABC 1 5, 10, 19 (5, 9) 2 8, 13, 23 (5, 10) 3 9, 14, 23 (5, 9) 4 13, 19, 29 (6, 10) ABCD 1 10, 19, 27 (9, 8) 2 13, 23, 31 (10, 8) 3 14, 23, 31 (9, 8) 4 19, 29, 37 (10, 8) 5, 10, 19, 27 (5, 9, 8) 2 BCD 1 8, 13, 23, 31 (5, 10, 8 ) 3 9, 14, 23, 31 (5, 9, 8) 4 13, 19, 29, 37 (6, 10, 8 )
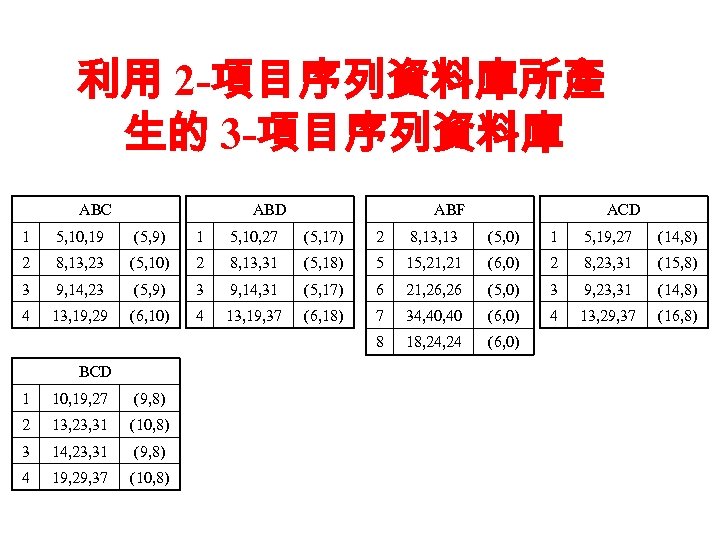利用 2 -項目序列資料庫所產 生的 3 -項目序列資料庫 ABC ABD ABF ACD 1 5, 10, 19 (5, 9) 1 5, 10, 27 (5, 17) 2 8, 13 (5, 0) 1 5, 19, 27 (14, 8) 2 8, 13, 23 (5, 10) 2 8, 13, 31 (5, 18) 5 15, 21 (6, 0) 2 8, 23, 31 (15, 8) 3 9, 14, 23 (5, 9) 3 9, 14, 31 (5, 17) 6 21, 26 (5, 0) 3 9, 23, 31 (14, 8) 4 13, 19, 29 (6, 10) 4 13, 19, 37 (6, 18) 7 34, 40 (6, 0) 4 13, 29, 37 (16, 8) 8 18, 24 (6, 0) BCD 1 10, 19, 27 (9, 8) 2 13, 23, 31 (10, 8) 3 14, 23, 31 (9, 8) 4 19, 29, 37 (10, 8)
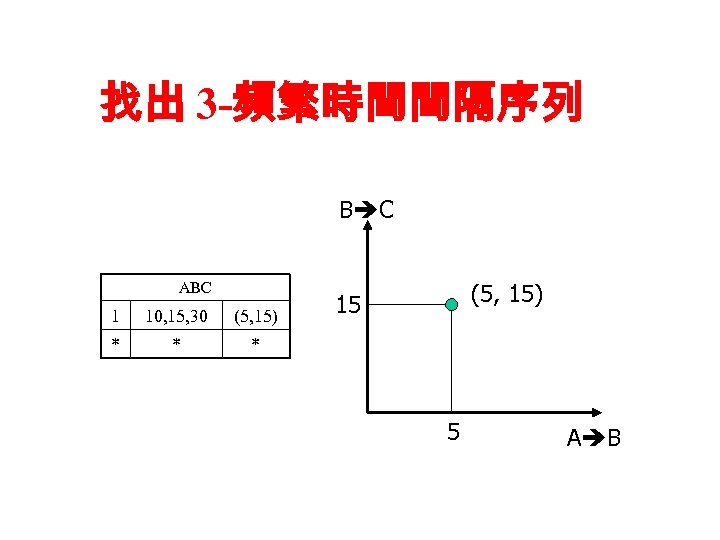找出 3 -頻繁時間間隔序列 B C ABC 1 10, 15, 30 (5, 15) * * (5, 15) 15 * 5 A B
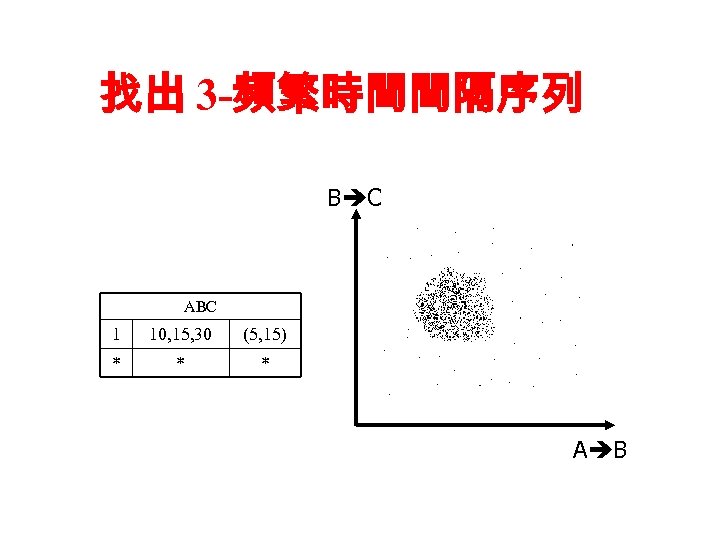找出 3 -頻繁時間間隔序列 B C ABC 1 10, 15, 30 (5, 15) * * * A B
![找出 3 -頻繁時間間隔序列 B C 輸出頻繁時間間隔序 列 B C A [15, 39] [25, 34]](https://present5.com/presentation/f9219563b4d441532c98093e53495a13/image-59.jpg "找出 3 -頻繁時間間隔序列 B C 輸出頻繁時間間隔序 列 B C A [15, 39] [25, 34]")
找出 3 -頻繁時間間隔序列 B C 輸出頻繁時間間隔序 列 B C A [15, 39] [25, 34] 40 35 輸出頻繁時間間隔序 列 B C A [20, 34] [20, 39] 25 20 15 20 35 40 A B 刪減項目序列 ABC 資料列表中 的資料
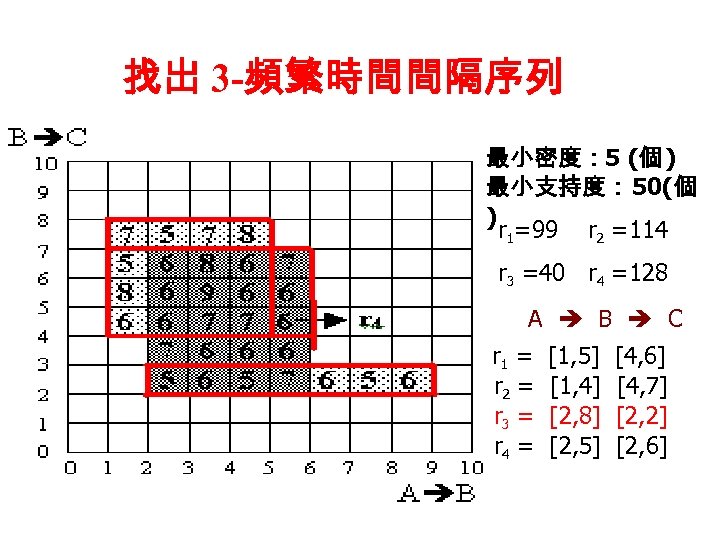找出 3 -頻繁時間間隔序列 最小密度： 5 (個 ) 最小支持度： 50(個 ) r 1=99 r 2 =114 r 3 =40 r 4 =128 A B C r 1 = r 2 = r 3 = r 4 = [1, 5] [1, 4] [2, 8] [2, 5] [4, 6] [4, 7] [2, 2] [2, 6]
![找出 3 -頻繁時間間隔序列 r 2 A B C r 1 = [1, 5] [4,](https://present5.com/presentation/f9219563b4d441532c98093e53495a13/image-61.jpg "找出 3 -頻繁時間間隔序列 r 2 A B C r 1 = [1, 5] [4,")
找出 3 -頻繁時間間隔序列 r 2 A B C r 1 = [1, 5] [4, 6] r 2 = [1, 4] [4, 7] r 4 = [2, 5] [2, 6]
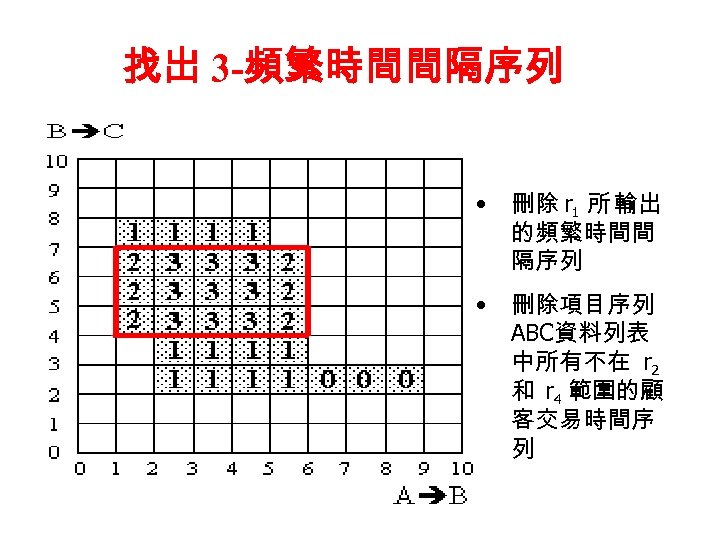找出 3 -頻繁時間間隔序列 • 刪除 r 1 所 輸出 的頻繁時間間 隔序列 • 刪除項目序列 ABC資料列表 中所有不在 r 2 和 r 4 範圍的顧 客交易時間序 列
3 -頻繁時間間隔序列 A B C A B D A C D B C D [5, 6] [9, 10] [13, 16] [7, 8] [5, 6] [17, 18] [9, 10] [7, 8] A B F [5, 6] [0, 0]
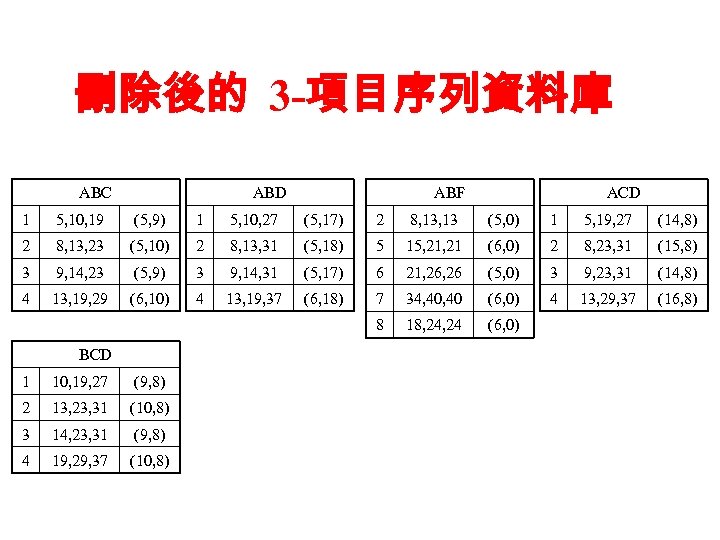刪除後的 3 -項目序列資料庫 ABC ABD ABF ACD 1 5, 10, 19 (5, 9) 1 5, 10, 27 (5, 17) 2 8, 13 (5, 0) 1 5, 19, 27 (14, 8) 2 8, 13, 23 (5, 10) 2 8, 13, 31 (5, 18) 5 15, 21 (6, 0) 2 8, 23, 31 (15, 8) 3 9, 14, 23 (5, 9) 3 9, 14, 31 (5, 17) 6 21, 26 (5, 0) 3 9, 23, 31 (14, 8) 4 13, 19, 29 (6, 10) 4 13, 19, 37 (6, 18) 7 34, 40 (6, 0) 4 13, 29, 37 (16, 8) 8 18, 24 (6, 0) BCD 1 10, 19, 27 (9, 8) 2 13, 23, 31 (10, 8) 3 14, 23, 31 (9, 8) 4 19, 29, 37 (10, 8)
利用 3 -項目序列資料庫所產 生的 4 -項目序列資料庫 ABCD 1 5, 10, 19, 27 (5, 9, 8) 2 8, 13, 23, 31 (5, 10, 8 ) 3 9, 14, 23, 31 (5, 9, 8) 4 13, 19, 29, 37 (6, 10, 8 )
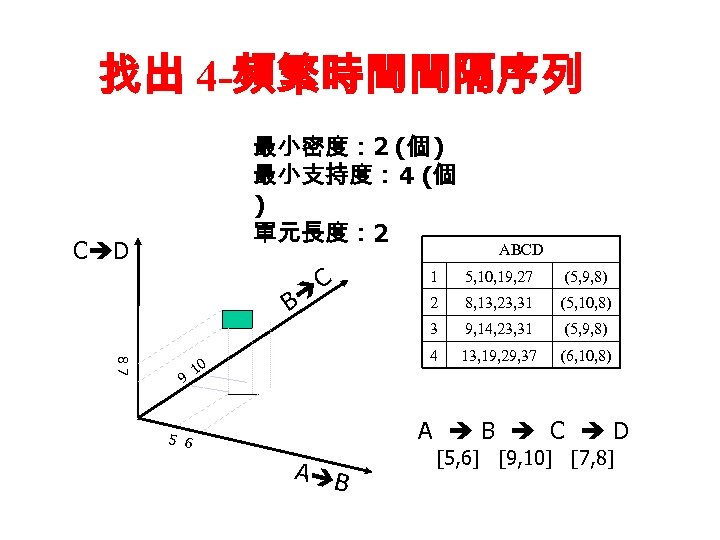找出 4 -頻繁時間間隔序列 最小密度： 2 (個 ) 最小支持度： 4 (個 ) 單元長度： 2 C D C ABCD 87 9 (5, 9, 8) 2 8, 13, 23, 31 (5, 10, 8) 9, 14, 23, 31 (5, 9, 8) 4 10 5, 10, 19, 27 3 B 1 13, 19, 29, 37 (6, 10, 8) A B C D 5 6 A B [5, 6] [9, 10] [7, 8]
![所有的頻繁時間間隔序列 A B A C A D B F C D [5, 6] [17,](https://present5.com/presentation/f9219563b4d441532c98093e53495a13/image-67.jpg "所有的頻繁時間間隔序列 A B A C A D B F C D [5, 6] [17,")
所有的頻繁時間間隔序列 A B A C A D B F C D [5, 6] [17, 18] [13, 16] [21, 24] [0, 0] A B D A C D B C D [13, 16] [7, 8] [5, 6] [17, 18] [9, 10] [7, 8] A B C D [5, 6] [9, 10] [7, 8] [5, 6] B C [9, 10] [7, 8] A B C [5, 6] [9, 10] A F A B F [5, 6] [0, 0]
![產生時間間隔序列型樣 頻繁時間間隔序 列 A B C 時間間隔序列型 樣 [5, 6] [9, 10] A B](https://present5.com/presentation/f9219563b4d441532c98093e53495a13/image-68.jpg "產生時間間隔序列型樣 頻繁時間間隔序 列 A B C 時間間隔序列型 樣 [5, 6] [9, 10] A B")
產生時間間隔序列型樣 頻繁時間間隔序 列 A B C 時間間隔序列型 樣 [5, 6] [9, 10] A B [3, 6] B C [7, 12] A B C [5, 6] [9, 10]
![時間間隔序列型樣 A B D [5, 6] [17, 18] A B F [5, 6] [0,](https://present5.com/presentation/f9219563b4d441532c98093e53495a13/image-69.jpg "時間間隔序列型樣 A B D [5, 6] [17, 18] A B F [5, 6] [0,")
時間間隔序列型樣 A B D [5, 6] [17, 18] A B F [5, 6] [0, 0] A C D [13, 16] [7, 8] A B C D [5, 6] [9, 10] [7, 8]
Important Issues • Discovering Episodes – Collection of ordered events within an interval – Web page C is accessed 2 min after A & B – Sliding Window Concept