Advanced Artificial Intelligence Part II Statistical NLP Introduction

Advanced Artificial Intelligence Part II. Statistical NLP Introduction and Grammar Models Wolfram Burgard, Luc De Raedt, Bernhard Nebel, Kristian Kersting Some slides taken from Helmut Schmid, Rada Mihalcea, Bonnie Dorr, Leila Kosseim, Peter Flach and others

Topic § Statistical Natural Language Processing § Applies • Machine Learning / Statistics to § • Learning : the ability to improve one’s behaviour at a specific task over time - involves the analysis of data (statistics) Natural Language Processing § Following parts of the book • Statistical NLP (Manning and Schuetze), MIT Press, 1999.

Contents § § Motivation Zipf’s law Some natural language processing tasks Non-probabilistic NLP models • Regular grammars and finite state automata • Context-Free Grammars • Definite Clause Grammars § Motivation for statistical NLP § Overview of the rest of this part

Rationalism versus Empiricism § Rationalist • • Noam Chomsky - innate language structures AI : hand coding NLP Dominant view 1960 -1985 Cf. e. g. Steven Pinker’s The language instinct. (popular science book) § Empiricist • • • Ability to learn is innate AI : language is learned from corpora Dominant 1920 -1960 and becoming increasingly important

Rationalism versus Empiricism § Noam Chomsky: • But it must be recognized that the notion of “probability of a sentence” is an entirely useless one, under any known interpretation of this term § Fred Jelinek (IBM 1988) • • Every time a linguist leaves the room the recognition rate goes up. (Alternative: Every time I fire a linguist the recognizer improves)

This course § Empiricist approach • Focus will be on probabilistic models for learning of natural language § No time to treat natural language in depth ! • • (though this would be quite useful and interesting) Deserves a full course by itself § Covered in more depth in Logic, Language and Learning (SS 05, prob. SS 06)

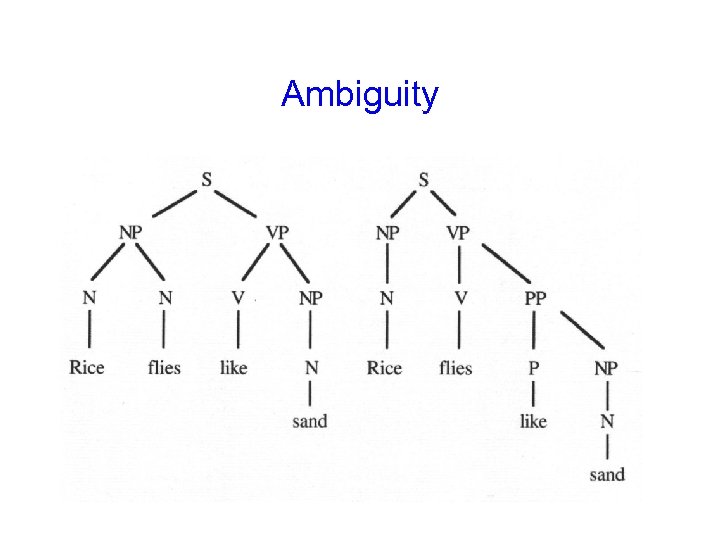Ambiguity

NLP and Statistics Statistical Disambiguation • Define a probability model for the data • Compute the probability of each alternative • Choose the most likely alternative

NLP and Statistics Statistical Methods deal with uncertainty. They predict the future behaviour of a system based on the behaviour observed in the past. Statistical Methods require training data. The data in Statistical NLP are the Corpora

Corpora § Corpus: text collection for linguistic purposes § Tokens How many words are contained in Tom Sawyer? 71. 370 § Types How many different words are contained in T. S. ? 8. 018 § Hapax Legomena words appearing only once

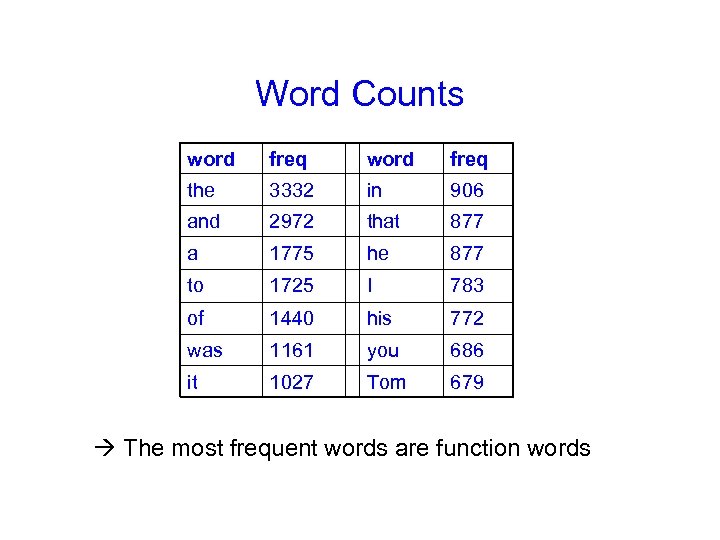Word Counts word freq the 3332 in 906 and 2972 that 877 a 1775 he 877 to 1725 I 783 of 1440 his 772 was 1161 you 686 it 1027 Tom 679 The most frequent words are function words

Word Counts f 1 2 3 4 5 6 7 8 9 10 11 -50 51 -100 > 100 nf 3993 1292 664 410 243 199 172 131 82 91 540 99 102 How many words appear f times? About half of the words occurs just once About half of the text consists of the 100 most common words ….

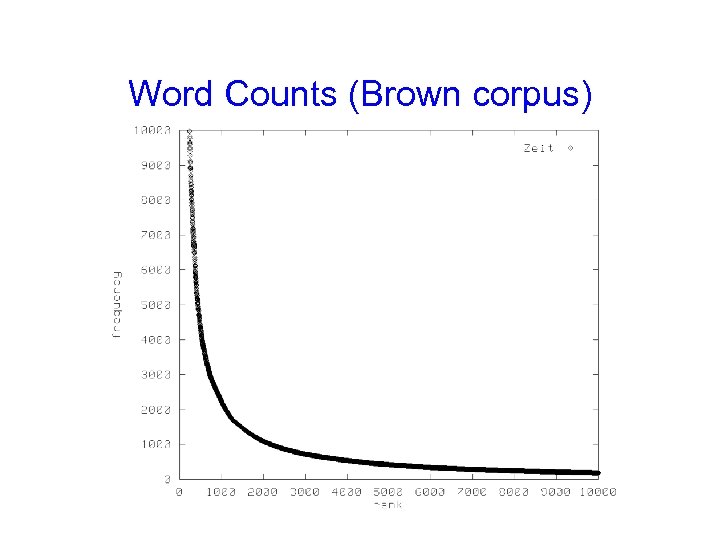Word Counts (Brown corpus)

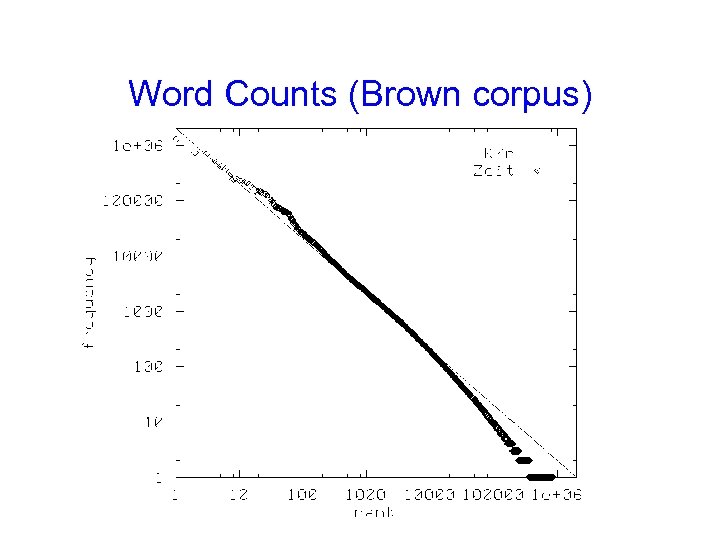Word Counts (Brown corpus)

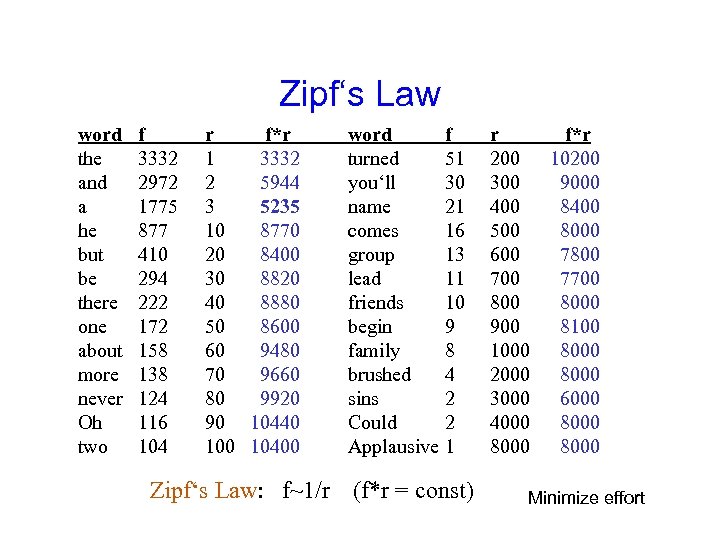Zipf‘s Law word the and a he but be there one about more never Oh two f 3332 2972 1775 877 410 294 222 172 158 138 124 116 104 r f*r 1 3332 2 5944 3 5235 10 8770 20 8400 30 8820 40 8880 50 8600 60 9480 70 9660 80 9920 90 10440 10400 Zipf‘s Law: f~1/r word turned you‘ll name comes group lead friends begin family brushed sins Could Applausive f 51 30 21 16 13 11 10 9 8 4 2 2 1 (f*r = const) r 200 300 400 500 600 700 800 900 1000 2000 3000 4000 8000 f*r 10200 9000 8400 8000 7800 7700 8000 8100 8000 6000 8000 Minimize effort

Language and sequences § Natural language processing • Is concerned with the analysis of sequences of words / sentences • Construction of language models § Two types of models • Non-probabilistic • Probabilistic

Key NLP Problem: Ambiguity Human Language is highly ambiguous at all levels • acoustic level recognize speech vs. wreck a nice beach • morphological level saw: to see (past), saw (noun), to saw (present, inf) • syntactic level I saw the man on the hill with a telescope • semantic level One book has to be read by every student

Language Model § A formal model about language § Two types • Non-probabilistic § Allows one to compute whether a certain sequence (sentence or part thereof) is possible § Often grammar based • Probabilistic § Allows one to compute the probability of a certain sequence § Often extends grammars with probabilities

Example of bad language model

A bad language model

A bad language model

A good language model § Non-Probabilistic • “I swear to tell the truth” is possible • “I swerve to smell de soup” is impossible § Probabilistic • P(I swear to tell the truth) ~. 0001 • P(I swerve to smell de soup) ~ 0

Why language models ? § Consider a Shannon Game • Predicting the next word in the sequence § Statistical natural language …. § The cat is thrown out of the … § The large green … § Sue swallowed the large green … §… § Model at the sentence level

Applications § § § Spelling correction Mobile phone texting Speech recognition Handwriting recognition Disabled users …

Spelling errors § They are leaving in about fifteen minuets to go to her house. § The study was conducted mainly be John Black. § Hopefully, all with continue smoothly in my absence. § Can they lave him my messages? § I need to notified the bank of…. § He is trying to fine out.

Handwriting recognition § Assume a note is given to a bank teller, which the teller reads as I have a gub. (cf. Woody Allen) § NLP to the rescue …. • gub is not a word • gun, gum, Gus, and gull are words, but gun has a higher probability in the context of a bank

For Spell Checkers § Collect list of commonly substituted words • piece/peace, whether/weather, their/there. . . § Example: “On Tuesday, the whether …’’ “On Tuesday, the weather …”

Another dimension in language models § Do we mainly want to infer (probabilities) of legal sentences / sequences ? • So far § Or, do we want to infer properties of these sentences ? • E. g. , parse tree, part-of-speech-tagging • Needed for understanding NL § Let’s look at some tasks

Sequence Tagging § Part-of-speech tagging • He drives with his bike • N V PR PN N noun, verb, preposition, pronoun, noun § Text extraction • The job is that of a programmer • X X X Job. Type • The seminar is taking place from 15. 00 to 16. 00 • X X X Start End

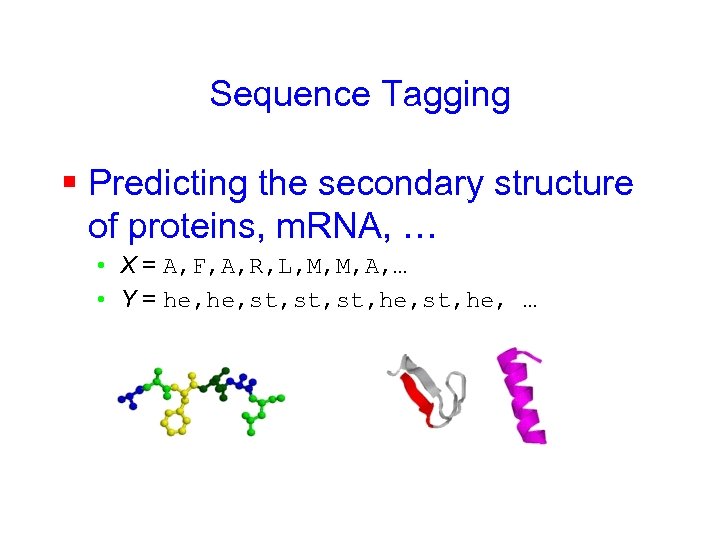Sequence Tagging § Predicting the secondary structure of proteins, m. RNA, … • X = A, F, A, R, L, M, M, A, … • Y = he, st, st, he, …

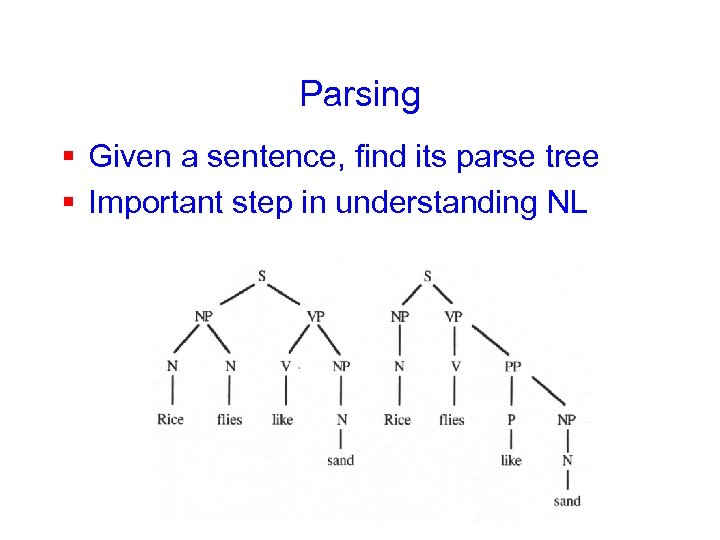Parsing § Given a sentence, find its parse tree § Important step in understanding NL

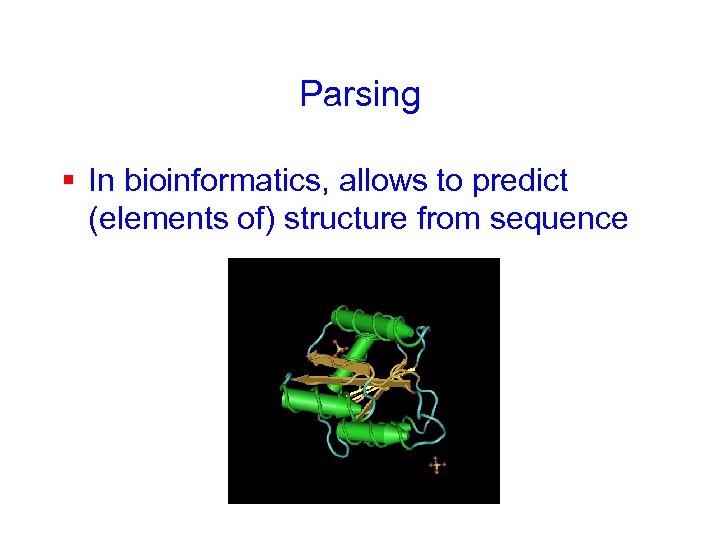Parsing § In bioinformatics, allows to predict (elements of) structure from sequence

Language models based on Grammars § Grammar Types • Regular grammars and Finite State Automata • Context-Free Grammars • Definite Clause Grammars § A particular type of Unification Based Grammar (Prolog) § Distinguish lexicon from grammar • Lexicon (dictionary) contains information about words, e. g. § word - possible tags (and possibly additional information) § flies - V(erb) - N(oun) • Grammar encode rules

Grammars and parsing § Syntactic level best understood and formalized § Derivation of grammatical structure: parsing (more than just recognition) § Result of parsing mostly parse tree: showing the constituents of a sentence, e. g. verb or noun phrases § Syntax usually specified in terms of a grammar consisting of grammar rules

Regular Grammars and Finite State Automata § Lexical information - which words are ? • • • § Det(erminer) N(oun) Vi (intransitive verb) - no argument Pn (pronoun) Vt (transitive verb) - takes an argument Adj (adjective) Now accept • • The cat slept Det N Vi § As regular grammar • S -> [Det] S 1 • S 1 -> [N] S 2 • S 2 -> [Vi] § Lexicon • The - Det • Cat - N • Slept - Vi • … % [ ] : terminal

Finite State Automaton § Sentences • • John smiles - Pn Vi The cat disappeared - Det N Vi These new shoes hurt - Det Adj N Vi John liked the old cat PN Vt Det Adj N

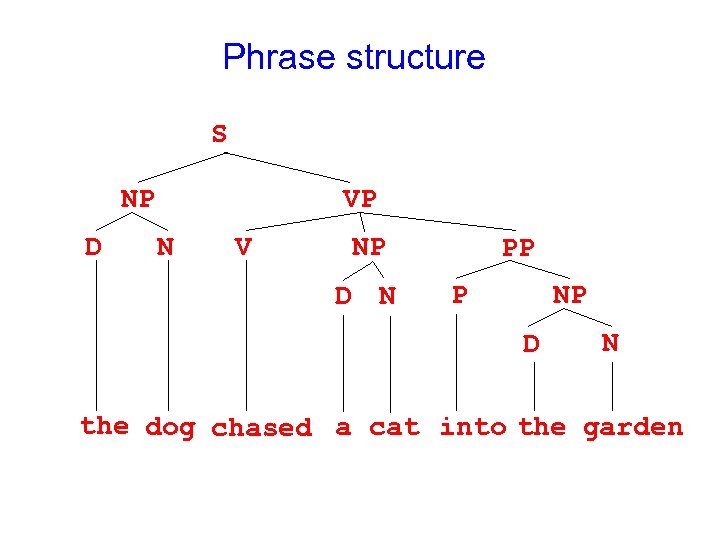Phrase structure S NP D VP N V NP D N PP P NP D N the dog chased a cat into the garden

Notation § § § § S: sentence D or Det: Determiner (e. g. , articles) N: noun V: verb P: preposition NP: noun phrase VP: verb phrase PP: prepositional phrase

Context Free Grammar S NP VP VP PP D D N N N V V P -> -> -> -> NP VP D N V NP PP P NP [the] [a] [dog] [cat] [garden] [chased] [saw] [into] Terminals ~ Lexicon

Phrase structure § Formalism of context-free grammars • Nonterminal symbols: S, NP, VP, . . . • Terminal symbols: dog, cat, saw, the, . . . § Recursion • „The girl thought the dog chased the cat“ VP N V -> V, S -> [girl] -> [thought]

Top-down parsing § § § § § S -> NP VP S -> Det N VP S -> The dog V NP S -> The dog chased Det N S-> The dog chased the cat

Context-free grammar S NP NP NP VP VP Art Adj PN N VI VT --> --> --> --> NP, VP. PN. %Proper noun Art, Adj, N. Art, N. VI. %intransitive verb VT, NP. %transitive verb [the]. [lazy]. [rapid]. [achilles]. [turtle]. [sleeps]. [beats].

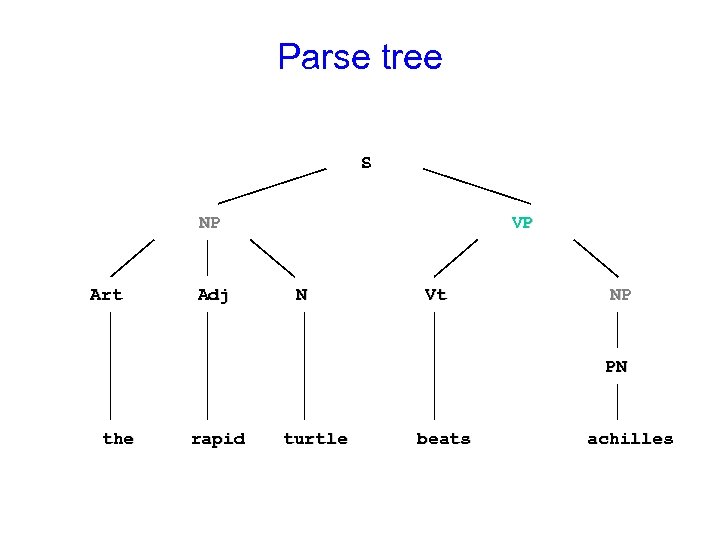Parse tree S NP Art Adj VP N Vt NP PN the rapid turtle beats achilles

Definite Clause Grammars Non-terminals may have arguments S --> NP(N), VP(N). NP(N) --> Art(N), N(N). VP(N) --> VI(N). Art(singular) --> [a]. Art(singular) --> [the]. Art(plural) --> [the]. N(singular) --> [turtle]. N(plural) --> [turtles]. VI(singular) --> [sleeps]. VI(plural) --> [sleep]. Number Agreement

DCGs § Non-terminals may have arguments • Variables (start with capital) § E. g. Number, Any • Constants (start with lower case) § E. g. singular, plural • Structured terms (start with lower case, and take arguments themselves) § E. g. vp(V, NP) § Parsing needs to be adapted • Using unification

Unification in a nutshell (cf. AI course) § Substitutions E. g. {Num / singular } {T / vp(V, NP)} § Applying substitution • Simultaneously replace variables by corresponding terms • S(Num) {Num / singular } = S(singular)

Unification § Take two non-terminals with arguments and compute (most general) substitution that makes them identical, e. g. , • Art(singular) and Art(Num) § Gives { Num / singular } • Art(singular) and Art(plural) § Fails • Art(Num 1) and Art(Num 2) § {Num 1 / Num 2} • PN(Num, accusative) and PN(singular, Case) § {Num/singular, Case/accusative}

Parsing with DCGs § Now require successful unification at each step § S -> NP(N), VP(N) § S -> Art(N), N(N), VP(N) {N/singular} § S -> a N(singular), VP(singular) § S -> a turtle sleeps § S-> a turtle sleep fails

Case Marking PN(singular, nominative) --> [he]; [she] PN(singular, accusative) --> [him]; [her] PN(plural, nominative) --> [they] PN(plural, accusative) --> [them] S --> NP(Number, nominative), NP(Number) VP(Number) --> V(Number), VP(Any, accusative) VP(Number, Case) VP(Number, Any) --> PN(Number, Case) --> Det, N(Number) He sees her. She sees him. They see her. But not Them see he.

DCGs § Are strictly more expressive than CFGs § Can represent for instance • • S(N) -> A(N), B(N), C(N) A(0) -> [] B(0) -> [] C(0) -> [] A(s(N)) -> A(N), [A] B(s(N)) -> B(N), [B] C(s(N)) -> C(N), [C]

Probabilistic Models § Traditional grammar models are very rigid, • essentially a yes / no decision § Probabilistic grammars • Define a probability models for the data • Compute the probability of each alternative • Choose the most likely alternative § Ilustrate on • Shannon Game • Spelling correction • Parsing

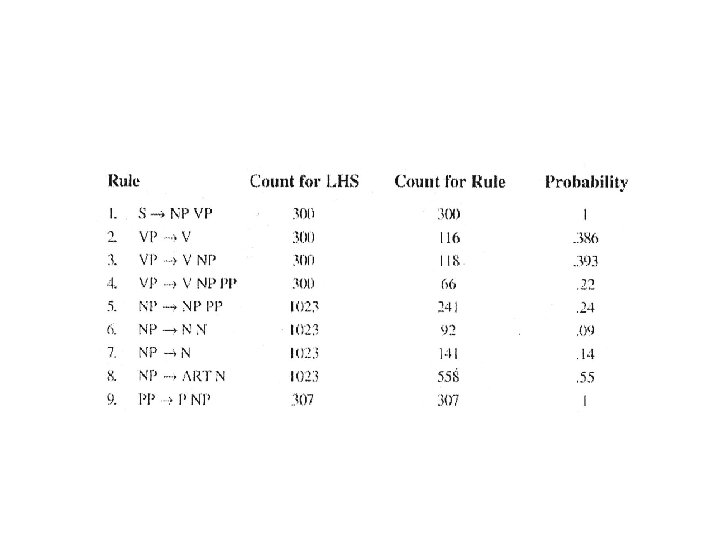
Illustration § Wall Street Journal Corpus § 3 000 words § Correct parse tree for sentences known • Constructed by hand • Can be used to derive stochastic context free grammars • SCFG assign probability to parse trees § Compute the most probable parse tree

Sequences are omni-present § Therefore the techniques we will see also apply to • Bioinformatics § DNA, proteins, m. RNA, … can all be represented as strings • Robotics § Sequences of actions, states, … • …

Rest of the Course § Limitations traditional grammar models motivate probabilistic extensions • Regular grammars and Finite State Automata § § All use principles of Part I on Graphical Models Markov Models using n-gramms (Hidden) Markov Models Conditional Random Fields • As an example of using undirected graphical models • Probabilistic Context Free Grammars • Probabilistic Definite Clause Grammars