Admission Control and Dynamic Adaptation for a Proportional-Delay

Admission Control and Dynamic Adaptation for a Proportional-Delay Diff. Serv-Enabled Web Server Yu Cai

Paper • Admission Control and Dynamic Adaptation for a Proportional-Delay Diff. Serv-Enabled Web Server • Sam C. M. Lee, John C. S. Lui, David K. Y. Yau • SIGMETRICS 2002

Why this paper? • Information fusion in distributed environment. • Data transmission from multiple sources with Qo. S requirements. – Then come to real data fusion techniques. – Data transmission is related to our specialties and my thesis. • Paper last week: video stream – a carefully designed scheme to define the data transmission unit: avoid overhead and provide flexibility. – data transmission through multiple path: algorithm

Summary of this paper • A web server that can provide proportionaldelay differentiated services to clients with different Qo. S requirements. – 3 classes - 1, 2, 3 – average waiting time of class 1 W 1=1. 4 * W 2 – W 2=1. 4 * W 3 – Real world example: an e-commerce site: general browsing - 1; client in the process of buying - 2; client check out - 3

Summary of this paper • Admission control and class assignment – 6 clients : a, b, c, d, e, f, g – with maximum traffic rate (work load) λmax – with maximum average waiting time (Qo. S) Wmax • Admit clients to different classes and meet the Qo. S requirements – class vector C={1, 2, 1, 1, 3, 1}

Summary of this paper • Dynamic class adaptation – Previous step is based on the maximum client workload λmax – Dynamically adjust the service classes based on the client real traffic condition – C={1, 2, 1, 1, 3, 1} => C={1, 2, 1, 1, 2, 1} • Goal: admit client to the lowest possible class while meeting the Qo. S requirements – The higher class is, the higher price to pay

Formulation • 3 classes: 1, 2, 3 – W 1=1. 4 * W 2; W 2=1. 4 * W 3 • 6 clients: a, b, c, d, e, f, g – with λmax, Wmax • Class vector C={1, 2, 1, 1, 3, 1} • Considerations when admit a client – Is it possible to admit the client with the Qo. S? – All other admitted clients need to keep the Qo. S – Assign lowest classes if possible

Formulation • Based on conservation law: – – λ 1* W 1 + λ 2* W 2 + λ 3* W 3 = (λ 1 + λ 2 + λ 3)*W W is measurable, λ 1, λ 2, λ 3 is measurable. W 1 = 1. 4 * W 2 ; W 3 = 1/1. 4 * W 2 λ 1* 1. 4 * W 2 + λ 2* W 2 + λ 3 / 1. 4 * W 2 = (λ 1 + λ 2 + λ 3)*W – So W 2 = (λ 1 + λ 2 + λ 3)*W / (λ 1* 1. 4 + λ 2+ λ 3 / 1. 4) – similarly W 1 and W 3 • Out goal is to maximize : – V = 1/ W 1 + 1/ W 2 + 1/ W 3 – Same as minimize the sum of Wi

Original formula

Admission control algorithms • Maximum Profit Algorithm (MPA) • Rationale: – two clients i and j with requirements of Wmaxi and Wmaxj – Wmaxi < Wmaxj , – client i is willing to pay a higher usage cost than client j so as to receive better service. – By admitting client i, the service provider may obtain a higher profit. – admit a client who has a more stringent maximum average waiting time requirement first.

MPA • Sort Wa<=Wb<=Wc<=Wd<=We<=Wf • For i=1 to 6{ – Assign client i in class 1 – While{ • Compute delay of all admitted clients • If all admitted clients meet Qo. S, admit client i, quit while • If some admitted clients don’t meet Qo. S – If anyone of them is in the lowest class N, then » stop admitting client i, quit while//impossible to admit – Else » increase all their classes by 1//update class – }//end while • }//end for

MPA analysis • In essence, MPA is a greedy algorithm. Therefore it can only give local optimal. It likely will not achieve the global optimal. • The authors kind of mislead the readers by making a vague and complicated definition: “MPA can always give a minimum feasible admitted class vector” – Sounds like global optimal, but still local optimal – C= {2, 2, 1, 1, 3, 1}; C 1={1, 2, 1, 1, 3, 1}; C 2={2, 1, 1, 1, 3, 1} – MPA knows C 1 and C 2 are better than C, but can not decide which is better between C 1 and C 2

MPA analysis • MPA updates all the unsatisfied clients’ class by 1, which adjust too much. • C 1={1, 2, 1, 1, 3, 1} => C 2={2, 3, 1, 1, 3, 2}; • But probably C 3={2, 2, 1, 1, 3, 2} is enough, or perhaps C 4={3, 1, 1, 1, 3, 2} is better

Maximum Admission Algorithm (MAA) • Rationale: – Admit as many clients as possible to popularize the site – Admit clients with larger maximum average waiting time first, because they consume less resources. – Still greedy algorithm, same local optimal problem and adjust too much problem.

Dynamic Class Adaptation • Why – AC is based on the maximum client workload λmax – Need to dynamically adjust the service classes based on the real traffic condition • Measurement window: a period of time for web server to estimate the client arrival rate. • Assumption: no major change in the future workload.

SBDA • Centralized Approach: Server-Based Dynamic Adaptation (SBDA) – Server measures the client arrival rate λ – Server use λ as λmax to calculate the class vector – Server send this vector info to clients – Client then get the upper bound of the class to choose from. Client needs to choose the lowest possible class – Say, client b get class 2 assigned from server, it means if client choose class 2, the server guarantee the Qo. S; so the client needs to decide if it can go lower to class 1; if yes, use class 1, if no, use class 2.

CBDA • SBDA drawbacks – Computation complexity – Communication overhead: unicast • Distributed & Game-Theoretic Approach: Client- Based Dynamic Adaptation (CBDA) – Server measure and estimate the arrival rate for each class – Server multicast the information – Client can determine its lowest class based on the received information and its own arrival rate information

CBDA • In essence, this is a non-cooperative game problem in which distributed optimization is performed by each client • Guaranteed termination: upper bound is given in Admission control. • Low computational complexity: client can even ignore this step.

My questions • A typical client traffic pattern is like this: – 80 % is λmax , 10 % is 0. 9 * λmax , 10 % is 0. 8 * λmax – Is this a realistic traffic pattern? – If traffic changes too much, the result seems to get bad. • Algorithm improvement. Greedy? adjust too much? • No simulation or analysis on how much the MPA and MAA is different from the optimal result

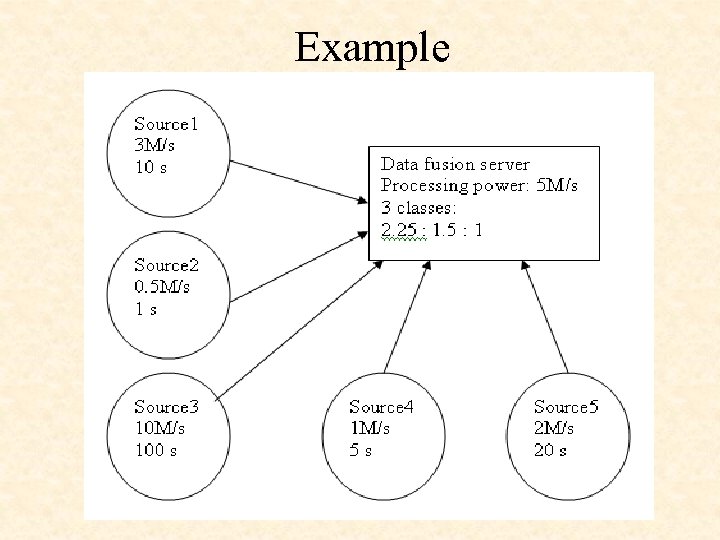
For our project • Multiple data sources with different Qo. S and different data amount/load, • Server side has a fixed data fusion ability • how to admit and classify the data into different classes based on the data load and server capacity while keeping the Qo. S?

Example