63e66c2b254edd8f8dbd0ecf7ba296df.ppt
- Количество слайдов: 98
 Adleman and computing on a surface
Adleman and computing on a surface
 Course outline 1 Introduction 2 Theoretical background Biochemistry/molecular biology 3 Theoretical background computer science 4 History of the field 5 Splicing systems 6 P systems 7 Hairpins 8 Detection techniques 9 Micro technology introduction 10 Microchips and fluidics 11 Self assembly 12 Regulatory networks 13 Molecular motors 14 DNA nanowires 15 Protein computers 16 DNA computing - summery 17 Presentation of essay and discussion
Course outline 1 Introduction 2 Theoretical background Biochemistry/molecular biology 3 Theoretical background computer science 4 History of the field 5 Splicing systems 6 P systems 7 Hairpins 8 Detection techniques 9 Micro technology introduction 10 Microchips and fluidics 11 Self assembly 12 Regulatory networks 13 Molecular motors 14 DNA nanowires 15 Protein computers 16 DNA computing - summery 17 Presentation of essay and discussion
 Who’s who?
Who’s who?
 Tom Head Department of Mathematical Sciences Binghamton University Areas of interest Algebra Computing with biomolecules Formal representations of communication http: //www. math. binghamton. edu/tom/
Tom Head Department of Mathematical Sciences Binghamton University Areas of interest Algebra Computing with biomolecules Formal representations of communication http: //www. math. binghamton. edu/tom/
 Leonard Adleman Department of Computer Science Turing Award 2002 Areas of interest 8 Method for Obtaining Digital Signatures and Public-Key Cryptosystems 8 Distinguishing Prime Numbers From Composite Numbers 8 The First Case of Fermat's Last Theorem 8 Primality Testing And Two Dimensional Abelian Varieties Over Finite Fields 8 Molecular Computation of Solutions To Combinatorial Problem http: //www. usc. edu/dept/molecular-science/fm-adleman. htm
Leonard Adleman Department of Computer Science Turing Award 2002 Areas of interest 8 Method for Obtaining Digital Signatures and Public-Key Cryptosystems 8 Distinguishing Prime Numbers From Composite Numbers 8 The First Case of Fermat's Last Theorem 8 Primality Testing And Two Dimensional Abelian Varieties Over Finite Fields 8 Molecular Computation of Solutions To Combinatorial Problem http: //www. usc. edu/dept/molecular-science/fm-adleman. htm
 Richard Lipton Theoretical Computer Science College of Computing, Georgia Tech Areas of interest 8 Algorithms and Complexity Theory 8 Cryptography 8 DNA Computing http: //www. cc. gatech. edu/computing/Theory/theory. html
Richard Lipton Theoretical Computer Science College of Computing, Georgia Tech Areas of interest 8 Algorithms and Complexity Theory 8 Cryptography 8 DNA Computing http: //www. cc. gatech. edu/computing/Theory/theory. html
 Laura Landweber Dept. of Ecology and Evolutionary Biology Princeton University Areas of interest 8 Origins of Genes, Genomes 8 the Genetic Code 8 Early Pathways of RNA Evolution 8 Scrambled Genes 8 RNA Editing 8 Gene Scrambling 8 DNA Computing http: //www. princeton. edu/~lfl/
Laura Landweber Dept. of Ecology and Evolutionary Biology Princeton University Areas of interest 8 Origins of Genes, Genomes 8 the Genetic Code 8 Early Pathways of RNA Evolution 8 Scrambled Genes 8 RNA Editing 8 Gene Scrambling 8 DNA Computing http: //www. princeton. edu/~lfl/
 John Reif Computer Science Duke University Areas of interest 8 DNA nanostructures 8 Molecular Computation 8 Efficient Algorithms 8 Parallel Computation 8 Robotic Motion Planning 8 Optical Computing. http: //www. cs. duke. edu/~reif/
John Reif Computer Science Duke University Areas of interest 8 DNA nanostructures 8 Molecular Computation 8 Efficient Algorithms 8 Parallel Computation 8 Robotic Motion Planning 8 Optical Computing. http: //www. cs. duke. edu/~reif/
 Erik Winfree Computer Science Computation and Neural Systems Caltech, Mac. Arthur Fellow 2000 Areas of interest 8 DNA-based computers 8 Computing by self-assembly 8 Genetic Regulatory Networks 8 Signal Transduction Cascades 8 Ribosomal Translation 8 DNA and RNA folding http: //www. dna. caltech. edu/~winfree/
Erik Winfree Computer Science Computation and Neural Systems Caltech, Mac. Arthur Fellow 2000 Areas of interest 8 DNA-based computers 8 Computing by self-assembly 8 Genetic Regulatory Networks 8 Signal Transduction Cascades 8 Ribosomal Translation 8 DNA and RNA folding http: //www. dna. caltech. edu/~winfree/
 Nadrian Seeman Department of Chemistry New York University Areas of interest 8 DNA Nanotechnology 8 Macromolecular Design and Topology 8 Biophysical Chemistry of Recombinational Intermediates 8 DNA-Based Computation 8 Crystallography http: //www. nyu. edu/pages/chemistry/faculty/seeman. html
Nadrian Seeman Department of Chemistry New York University Areas of interest 8 DNA Nanotechnology 8 Macromolecular Design and Topology 8 Biophysical Chemistry of Recombinational Intermediates 8 DNA-Based Computation 8 Crystallography http: //www. nyu. edu/pages/chemistry/faculty/seeman. html
 Robert Corn Chemistry Department University of Wisconsin Areas of interest 8 surface plasmon resonance (SPR) to monitor biopolymer adsorption, the chemical modification of surfaces, 8 characterization of molecular monolayers 8 electron transfer processes at liquid/liquid electrochemical interfaces. DNA computing algorithms at surfaces 8 multilayer polyelectrolyte films for ion transport applications. http: //corninfo. chem. wisc. edu/
Robert Corn Chemistry Department University of Wisconsin Areas of interest 8 surface plasmon resonance (SPR) to monitor biopolymer adsorption, the chemical modification of surfaces, 8 characterization of molecular monolayers 8 electron transfer processes at liquid/liquid electrochemical interfaces. DNA computing algorithms at surfaces 8 multilayer polyelectrolyte films for ion transport applications. http: //corninfo. chem. wisc. edu/
 Hagiya Masami Department of Computer Science, University of Tokyo Areas of interest 8 Automated Deduction, Formal Verification and Programming Languages 8 Bio-Computing 8 Hybrid Systems. . . http: //hagi. is. s. u-tokyo. ac. jp
Hagiya Masami Department of Computer Science, University of Tokyo Areas of interest 8 Automated Deduction, Formal Verification and Programming Languages 8 Bio-Computing 8 Hybrid Systems. . . http: //hagi. is. s. u-tokyo. ac. jp
 Akira Suyama Graduate School of Arts and Sciences, University of Tokyo Areas of interest 8 SNPs 8 Probe design DNA chips 8 Quantitative gene expression 8 Hybrid Systems. . . http: //talent. c. u-tokyo. ac. jp/suyama/
Akira Suyama Graduate School of Arts and Sciences, University of Tokyo Areas of interest 8 SNPs 8 Probe design DNA chips 8 Quantitative gene expression 8 Hybrid Systems. . . http: //talent. c. u-tokyo. ac. jp/suyama/
 John Rose Department of Computer Science, University of Tokyo 1. Areas of interest 2. the DNA chip, especially Tag-Antitag Systems 3. Whiplash PCR, a simple autonomous DNA computer 4. equilibrium chemistry/statistical thermodynamic model http: //hagi. is. s. u-tokyo. ac. jp/~johnrose/
John Rose Department of Computer Science, University of Tokyo 1. Areas of interest 2. the DNA chip, especially Tag-Antitag Systems 3. Whiplash PCR, a simple autonomous DNA computer 4. equilibrium chemistry/statistical thermodynamic model http: //hagi. is. s. u-tokyo. ac. jp/~johnrose/
 Gheorghe Păun Institute of Mathematics of the Romanian Academy Areas of interest 8 Formal language theory (and applications) 8 Combinatorics on words 8 Semiotics 8 operational research 8 DNA Computing 8 Membrane Computing http: //stoilow. imar. ro/~gpaun/
Gheorghe Păun Institute of Mathematics of the Romanian Academy Areas of interest 8 Formal language theory (and applications) 8 Combinatorics on words 8 Semiotics 8 operational research 8 DNA Computing 8 Membrane Computing http: //stoilow. imar. ro/~gpaun/
 Grzegorz Rozenberg Institute of Advanced Computer Science University of Leiden Areas of interest 8 Molecular Computing 8 Evolutionary Algorithms 8 Neural Networks http: //www. wi. leidenuniv. nl/~rozenber/
Grzegorz Rozenberg Institute of Advanced Computer Science University of Leiden Areas of interest 8 Molecular Computing 8 Evolutionary Algorithms 8 Neural Networks http: //www. wi. leidenuniv. nl/~rozenber/
 Giancarlo Mauri Dipartimento di Informatica, Sistemistica e Comunicazione (DISCo) Milano Areas of interest 8 H systems 8 P systems 8 Neural Networks http: //bioinformatics. bio. disco. unimib. it/
Giancarlo Mauri Dipartimento di Informatica, Sistemistica e Comunicazione (DISCo) Milano Areas of interest 8 H systems 8 P systems 8 Neural Networks http: //bioinformatics. bio. disco. unimib. it/
 Ehud Shapiro Computer Science and Applied Mathematics the Weizmann Institute Areas of interest 8 DNA as input fuel 8 Biological nanocomputer 8 Turing machine-like model http: //www. weizmann. ac. il/mathusers/lbn/index. html
Ehud Shapiro Computer Science and Applied Mathematics the Weizmann Institute Areas of interest 8 DNA as input fuel 8 Biological nanocomputer 8 Turing machine-like model http: //www. weizmann. ac. il/mathusers/lbn/index. html
 Byoung-Tak Zhang School of Computer Science and Engineering Seoul National University Areas of interest 8 Evolutionary Intelligence 8 Neural Intelligence 8 Molecular Intelligence 8 Computational Learning Theory http: //scai. snu. ac. kr/~btzhang/
Byoung-Tak Zhang School of Computer Science and Engineering Seoul National University Areas of interest 8 Evolutionary Intelligence 8 Neural Intelligence 8 Molecular Intelligence 8 Computational Learning Theory http: //scai. snu. ac. kr/~btzhang/
 Danny van Noort School of Computer Science and Engineering Seoul National University Areas of interest 8 microstructure design and fabrication 8 DNA-hybridisation 8 instrumentation 8 fluorescent microscopy 8 affinity biosensors 8 protein chips 8 DNA computing 8 cell behaviour http: //bi. snu. ac. kr/~danny/
Danny van Noort School of Computer Science and Engineering Seoul National University Areas of interest 8 microstructure design and fabrication 8 DNA-hybridisation 8 instrumentation 8 fluorescent microscopy 8 affinity biosensors 8 protein chips 8 DNA computing 8 cell behaviour http: //bi. snu. ac. kr/~danny/
 NP complete problems
NP complete problems
 The theory of NP-completeness 8 Tractable and intractable problems 8 NP-complete problems
The theory of NP-completeness 8 Tractable and intractable problems 8 NP-complete problems
 Classifying problems 8 Classify problems as tractable or intractable. 8 Problem is tractable if there exists at least one polynomial bound algorithm that solves it. 8 An algorithm is polynomial bound if its worst case growth rate can be bound by a polynomial p(n) in the size n of the problem
Classifying problems 8 Classify problems as tractable or intractable. 8 Problem is tractable if there exists at least one polynomial bound algorithm that solves it. 8 An algorithm is polynomial bound if its worst case growth rate can be bound by a polynomial p(n) in the size n of the problem
 Intractable problems • Problem is intractable if it is not tractable. • All algorithms that solve the problem are not polynomial bound. • It has a worst case growth rate f(n) which cannot be bound by a polynomial p(n) in the size n of the problem. • For intractable problems the bounds are:
Intractable problems • Problem is intractable if it is not tractable. • All algorithms that solve the problem are not polynomial bound. • It has a worst case growth rate f(n) which cannot be bound by a polynomial p(n) in the size n of the problem. • For intractable problems the bounds are:
 Hard practical problems 8 There are many practical problems for which no one has yet found a polynomial bound algorithm. 8 Examples: traveling salesperson, 0/1 knapsack, graph coloring, bin packing etc. 8 Most design automation problems such as testing and routing. 8 Many networks, database and graph problems.
Hard practical problems 8 There are many practical problems for which no one has yet found a polynomial bound algorithm. 8 Examples: traveling salesperson, 0/1 knapsack, graph coloring, bin packing etc. 8 Most design automation problems such as testing and routing. 8 Many networks, database and graph problems.
 The theory of NP-completeness 8 The theory of NP-completeness enables showing that these problems are at least as hard as NP-complete problems 8 Practical implication of knowing problem is NP-complete is that it is probably intractable ( whether it is or not has not been proved yet) 8 So any algorithm that solves it will probably be very slow for large inputs
The theory of NP-completeness 8 The theory of NP-completeness enables showing that these problems are at least as hard as NP-complete problems 8 Practical implication of knowing problem is NP-complete is that it is probably intractable ( whether it is or not has not been proved yet) 8 So any algorithm that solves it will probably be very slow for large inputs
 Decision problems 8 A decision problem answers yes or no for a given input 8 Examples: 9 Given a graph G Is there a path from s to t of length at most k? 9 Does graph G contain a Hamiltonian cycle? 9 Given a graph G is it bipartite?
Decision problems 8 A decision problem answers yes or no for a given input 8 Examples: 9 Given a graph G Is there a path from s to t of length at most k? 9 Does graph G contain a Hamiltonian cycle? 9 Given a graph G is it bipartite?
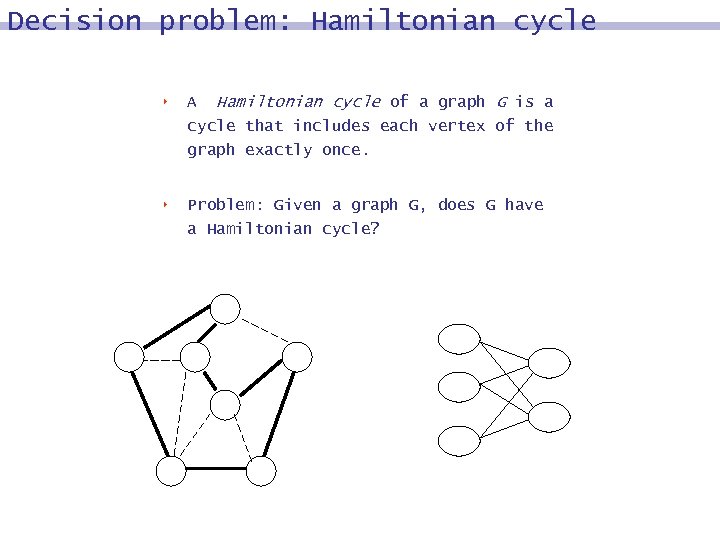 Decision problem: Hamiltonian cycle 8 A Hamiltonian cycle of a graph G is a cycle that includes each vertex of the graph exactly once. 8 Problem: Given a graph G, does G have a Hamiltonian cycle?
Decision problem: Hamiltonian cycle 8 A Hamiltonian cycle of a graph G is a cycle that includes each vertex of the graph exactly once. 8 Problem: Given a graph G, does G have a Hamiltonian cycle?
 The class P 8 P is the class of decision problems that are polynomial bounded 8 Is the following problem in P? 9 Given a weighted graph G, is there a spanning 8 tree of weight at most B? The decision versions of problems such as shortest distance, and minimum spanning tree belong to P
The class P 8 P is the class of decision problems that are polynomial bounded 8 Is the following problem in P? 9 Given a weighted graph G, is there a spanning 8 tree of weight at most B? The decision versions of problems such as shortest distance, and minimum spanning tree belong to P
 The class NP 8 NP is the class of decision problems for which there is a polynomial bounded verification algorithm 8 It can be shown that: 8 all decision problems in P, and 8 decision problems such as traveling salesman, knapsack, bin pack, are also in NP
The class NP 8 NP is the class of decision problems for which there is a polynomial bounded verification algorithm 8 It can be shown that: 8 all decision problems in P, and 8 decision problems such as traveling salesman, knapsack, bin pack, are also in NP
 The relation between P and NP 8 P Í NP 8 If a problem is solvable in polynomial time, a polynomial time verification algorithm can easily be designed that ignores the certificate and answers “yes” for all inputs with the answer “yes”.
The relation between P and NP 8 P Í NP 8 If a problem is solvable in polynomial time, a polynomial time verification algorithm can easily be designed that ignores the certificate and answers “yes” for all inputs with the answer “yes”.
 The relation between P and NP 8 It is not known whether 8 Problems in P can be solved “quickly” 8 Problems in NP can be verified “quickly”. 8 It is easier to verify a solution than to solve a problem. 8 Some researchers believe that P and NP are not the same class. P = NP.
The relation between P and NP 8 It is not known whether 8 Problems in P can be solved “quickly” 8 Problems in NP can be verified “quickly”. 8 It is easier to verify a solution than to solve a problem. 8 Some researchers believe that P and NP are not the same class. P = NP.
 NP-complete problems 8 A problem A is NP-complete if 1. It is in NP and 2. For every other problem A’ in NP, A’ µ A 8 A problem A is NP-hard if For every other problem A’ in NP, A’ µ A
NP-complete problems 8 A problem A is NP-complete if 1. It is in NP and 2. For every other problem A’ in NP, A’ µ A 8 A problem A is NP-hard if For every other problem A’ in NP, A’ µ A
 Examples of NP-complete problems 8 Cook’s theorem Satisfiability is NP-complete 8 This was the first problem shown to be NP-complete 8 Other problems the decision version of knapsack, the decision version of traveling salesman
Examples of NP-complete problems 8 Cook’s theorem Satisfiability is NP-complete 8 This was the first problem shown to be NP-complete 8 Other problems the decision version of knapsack, the decision version of traveling salesman
 Satisfiability problem
Satisfiability problem
 The satisfiability problem 8 First, Conjunctive Normal Form (CNF) will be defined 8 Then, the Satisfiability problem will be defined
The satisfiability problem 8 First, Conjunctive Normal Form (CNF) will be defined 8 Then, the Satisfiability problem will be defined
 Conjunctive normal form (CNF) 8 A logical (Boolean) variable is a variable that may be assigned the value true or false (x, y, w and z are Boolean variables) 8 A literal is a logical variable or the negation of a logical variable (x and y are literals) 8 A clause is a disjunction of literals ((w x y) and ( x y) are clauses)
Conjunctive normal form (CNF) 8 A logical (Boolean) variable is a variable that may be assigned the value true or false (x, y, w and z are Boolean variables) 8 A literal is a logical variable or the negation of a logical variable (x and y are literals) 8 A clause is a disjunction of literals ((w x y) and ( x y) are clauses)
 Conjunctive normal form (CNF) 8 A logical (Boolean) expression is in Conjunctive Normal Form if it is a conjunction of clauses. 8 The following expression conjunctive normal form: is in (w x y) (w y z) ( x y) ( w y)
Conjunctive normal form (CNF) 8 A logical (Boolean) expression is in Conjunctive Normal Form if it is a conjunction of clauses. 8 The following expression conjunctive normal form: is in (w x y) (w y z) ( x y) ( w y)
 The satisfiability problem 8 Is there a truth assignment to the n variables of a logical expression in Conjunctive Normal Form which makes the value of the expression true? 8 For the answer to be yes, all clauses must evaluate to true 8 Otherwise the answer is no
The satisfiability problem 8 Is there a truth assignment to the n variables of a logical expression in Conjunctive Normal Form which makes the value of the expression true? 8 For the answer to be yes, all clauses must evaluate to true 8 Otherwise the answer is no
 The satisfiability problem 8 x=F, y=F, w=T and z=T is a truth assignment for: (w x y) (w y z) ( x y) ( w y) 8 Note that if y=F then y=T 8 Each clause evaluates to true
The satisfiability problem 8 x=F, y=F, w=T and z=T is a truth assignment for: (w x y) (w y z) ( x y) ( w y) 8 Note that if y=F then y=T 8 Each clause evaluates to true
 Adleman’s experiment
Adleman’s experiment
 The 1994 experiment DNA computer
The 1994 experiment DNA computer
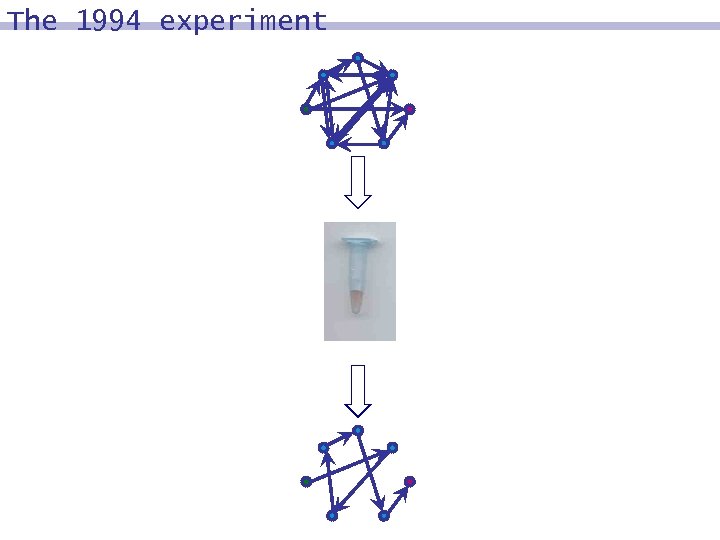 The 1994 experiment
The 1994 experiment
 The 1994 experiment Basic Idea Perform molecular biology experiment to find solution to math problem.
The 1994 experiment Basic Idea Perform molecular biology experiment to find solution to math problem.
 Hamiltonian path 8 (Proposed by William Hamilton) 8 Given a network of nodes and directed connections between them, is there a path through the network that begins with the start node and concludes with the end node visiting each node only once (“Hamiltonian path")? 8 Does a Hamiltonian path exist, or not? ”
Hamiltonian path 8 (Proposed by William Hamilton) 8 Given a network of nodes and directed connections between them, is there a path through the network that begins with the start node and concludes with the end node visiting each node only once (“Hamiltonian path")? 8 Does a Hamiltonian path exist, or not? ”
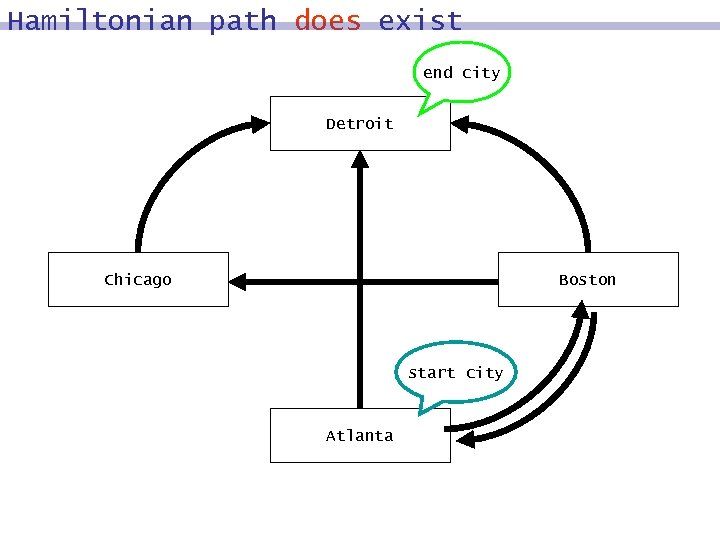 Hamiltonian path does exist end city Detroit Chicago Boston start city Atlanta
Hamiltonian path does exist end city Detroit Chicago Boston start city Atlanta
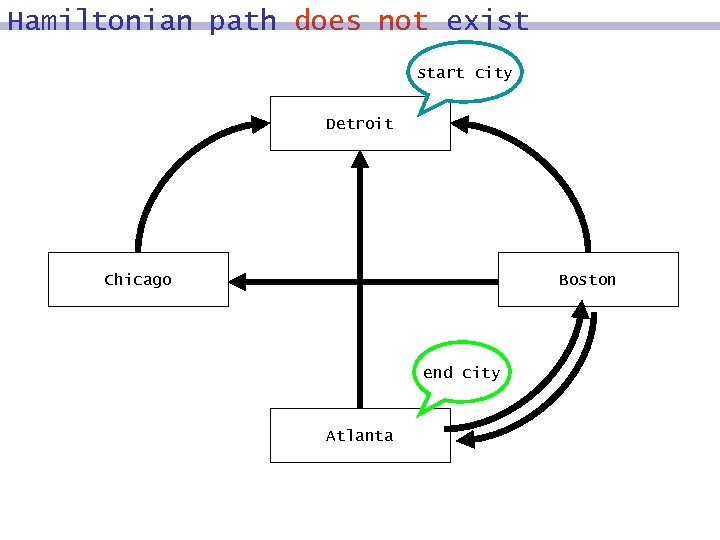 Hamiltonian path does not exist start city Detroit Chicago Boston end city Atlanta
Hamiltonian path does not exist start city Detroit Chicago Boston end city Atlanta
 Solving the Hamiltonian problem es, N Generation-&-Test Algorithm Step 1 Generate random paths on the network. Step 2 Keep start city and conclude with end city. are there. If Step 3 paths of length N. cities 4 at. Keep Step enter all those that only least once. Step Any 5 remaining are paths solutions (i. e. , Hamiltonian paths).
Solving the Hamiltonian problem es, N Generation-&-Test Algorithm Step 1 Generate random paths on the network. Step 2 Keep start city and conclude with end city. are there. If Step 3 paths of length N. cities 4 at. Keep Step enter all those that only least once. Step Any 5 remaining are paths solutions (i. e. , Hamiltonian paths).
![The paths [X] D -> B -> A [X] B -> C -> D The paths [X] D -> B -> A [X] B -> C -> D](https://present5.com/presentation/63e66c2b254edd8f8dbd0ecf7ba296df/image-49.jpg) The paths [X] D -> B -> A [X] B -> C -> D -> B -> A -> B [X] A -> B -> C -> B [X] C -> D -> B -> A [x] A -> B -> A -> D [O] A -> B -> C -> D [X] A -> B -> C -> D
The paths [X] D -> B -> A [X] B -> C -> D -> B -> A -> B [X] A -> B -> C -> B [X] C -> D -> B -> A [x] A -> B -> A -> D [O] A -> B -> C -> D [X] A -> B -> C -> D
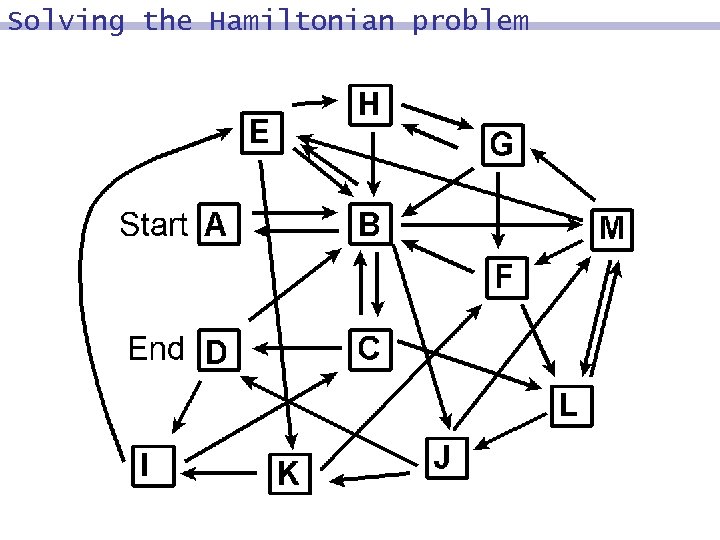 Solving the Hamiltonian problem
Solving the Hamiltonian problem
 Combinatorial explosion 8 The total number of paths grows exponentially as the network size increases: 8 (e. g. ) 106 paths for N=10 cities, 1012 paths (N=20), 10100 paths!! (N =100) 8 The Generation-&-Test algorithm takes “forever”. Some sort of smart algorithm must be devised; none has been found so far (NP-hard).
Combinatorial explosion 8 The total number of paths grows exponentially as the network size increases: 8 (e. g. ) 106 paths for N=10 cities, 1012 paths (N=20), 10100 paths!! (N =100) 8 The Generation-&-Test algorithm takes “forever”. Some sort of smart algorithm must be devised; none has been found so far (NP-hard).
 Finding a solution with DNA The key to solving the problem is using DNA to perform the five steps of the Generation-&Test algorithm in parallel search, instead of serial search.
Finding a solution with DNA The key to solving the problem is using DNA to perform the five steps of the Generation-&Test algorithm in parallel search, instead of serial search.
 Intermezzo: DNA polymerase 8 Protein that produces complementary DNA strand 8 A -> T, T -> A, C -> G, G -> C 8 Requires primer and starter 8 Enables DNA to reproduce
Intermezzo: DNA polymerase 8 Protein that produces complementary DNA strand 8 A -> T, T -> A, C -> G, G -> C 8 Requires primer and starter 8 Enables DNA to reproduce
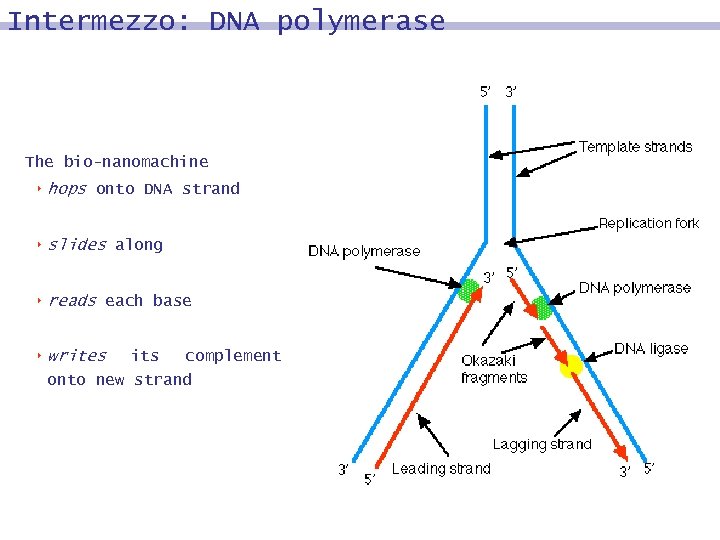 Intermezzo: DNA polymerase The bio-nanomachine 8 hops onto DNA strand 8 slides 8 reads 8 writes along each base its complement onto new strand
Intermezzo: DNA polymerase The bio-nanomachine 8 hops onto DNA strand 8 slides 8 reads 8 writes along each base its complement onto new strand
 Experimental set-up Ingredients and tools needed 8 DNA strands that encode city names and connections between them 8 Polymerases, ligase, water, salt, other ingredients 8 Polymerase chain reaction (PCR) set 8 Gel electrophoresis tool (that filters out non-solution strands)
Experimental set-up Ingredients and tools needed 8 DNA strands that encode city names and connections between them 8 Polymerases, ligase, water, salt, other ingredients 8 Polymerase chain reaction (PCR) set 8 Gel electrophoresis tool (that filters out non-solution strands)
 Gel electrophoresis
Gel electrophoresis
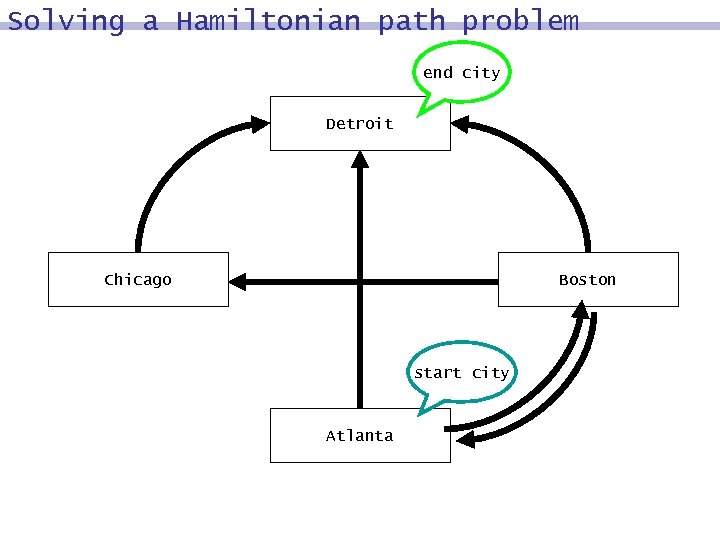 Solving a Hamiltonian path problem end city Detroit Chicago Boston start city Atlanta
Solving a Hamiltonian path problem end city Detroit Chicago Boston start city Atlanta
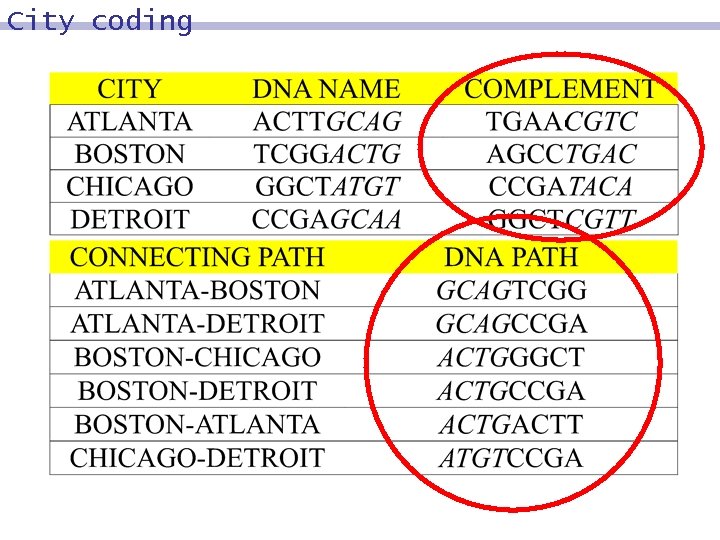 City coding
City coding
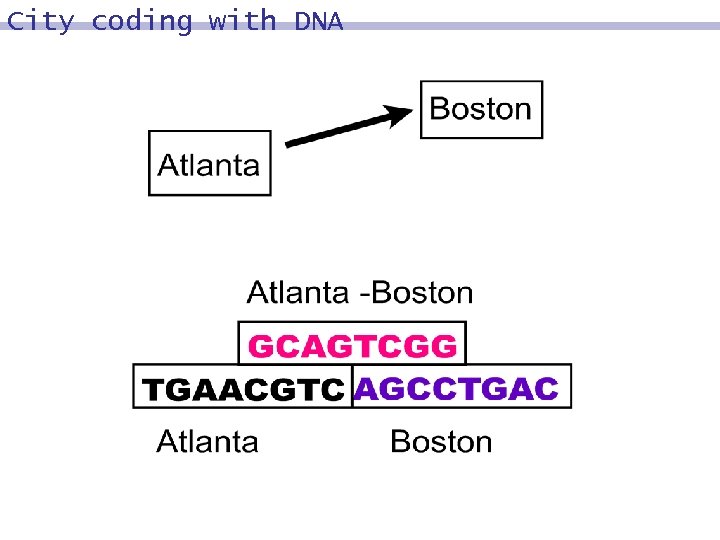 City coding with DNA
City coding with DNA
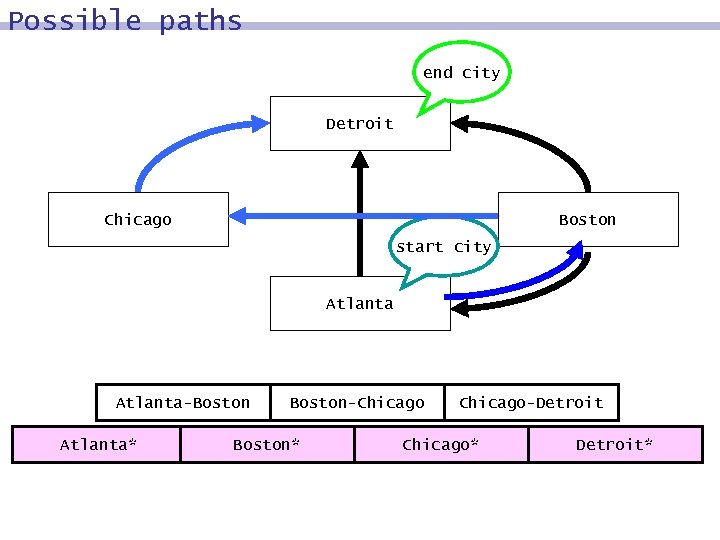 Possible paths end city Detroit Chicago Boston start city Atlanta-Boston Atlanta* Boston-Chicago Boston* Chicago-Detroit Chicago* Detroit*
Possible paths end city Detroit Chicago Boston start city Atlanta-Boston Atlanta* Boston-Chicago Boston* Chicago-Detroit Chicago* Detroit*
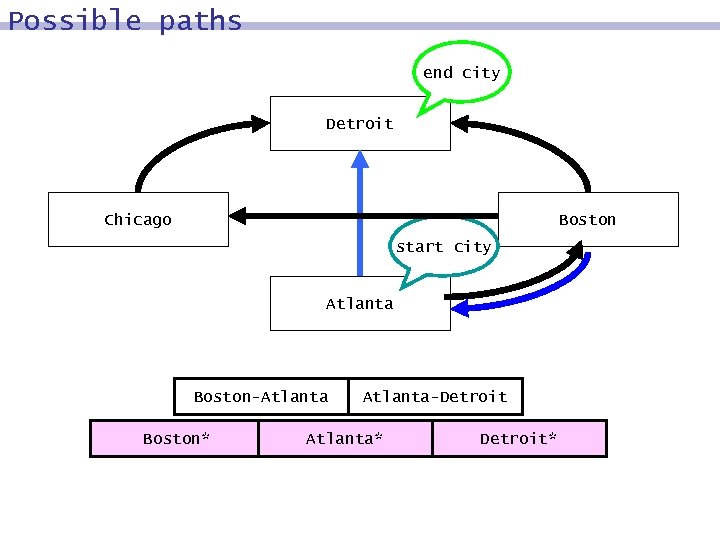 Possible paths end city Detroit Chicago Boston start city Atlanta Boston-Atlanta Boston* Atlanta-Detroit Atlanta* Detroit*
Possible paths end city Detroit Chicago Boston start city Atlanta Boston-Atlanta Boston* Atlanta-Detroit Atlanta* Detroit*
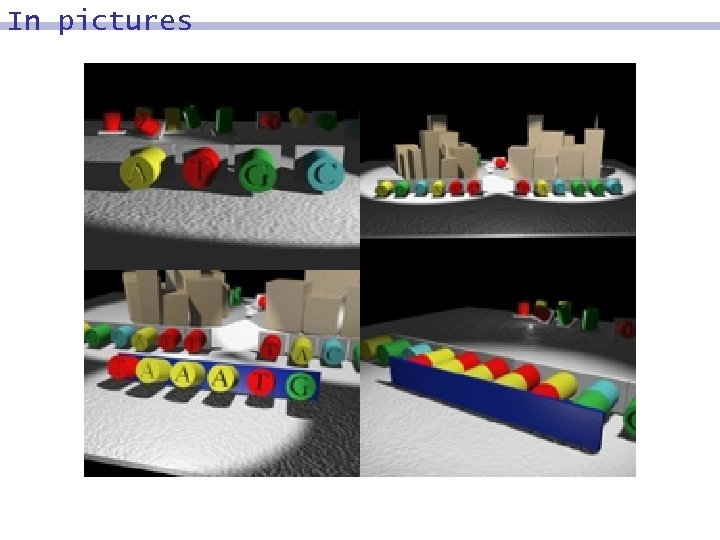 In pictures
In pictures
 The DNA experiment 1. In a test tube, mix the prepared DNA pieces together (which will randomly link with each other, forming all different paths). 2. Perform PCR with two ‘start’ and ‘end’ DNA pieces as primers (which creates millions’ copies of DNA strands with the right start and end). 3. Perform gel electrophoresis to identify only those pieces of right length (e. g. , N=4).
The DNA experiment 1. In a test tube, mix the prepared DNA pieces together (which will randomly link with each other, forming all different paths). 2. Perform PCR with two ‘start’ and ‘end’ DNA pieces as primers (which creates millions’ copies of DNA strands with the right start and end). 3. Perform gel electrophoresis to identify only those pieces of right length (e. g. , N=4).
 The DNA experiment 4. Use DNA ‘probe’ molecules to check whether their paths pass through all intermediate cities. 5. All DNA pieces that are left in the tube should be precisely those representing Hamiltonian paths. 9 If the tube contains any DNA at all, then conclude that a Hamiltonian path exists, and otherwise not. 9 When it does, the DNA sequence represents the specific path of the solution.
The DNA experiment 4. Use DNA ‘probe’ molecules to check whether their paths pass through all intermediate cities. 5. All DNA pieces that are left in the tube should be precisely those representing Hamiltonian paths. 9 If the tube contains any DNA at all, then conclude that a Hamiltonian path exists, and otherwise not. 9 When it does, the DNA sequence represents the specific path of the solution.
 Summary and conclusion Why does it work? 8 Enormous parallelism, with 1023 DNA pieces working in parallel to find solution simultaneously. 8 Takes less than a week (vs. thousands years for supercomputer) Extraordinary energy efficient 8 (10 -10 of supercomputer energy use) Note this is a Universal Turing machine
Summary and conclusion Why does it work? 8 Enormous parallelism, with 1023 DNA pieces working in parallel to find solution simultaneously. 8 Takes less than a week (vs. thousands years for supercomputer) Extraordinary energy efficient 8 (10 -10 of supercomputer energy use) Note this is a Universal Turing machine
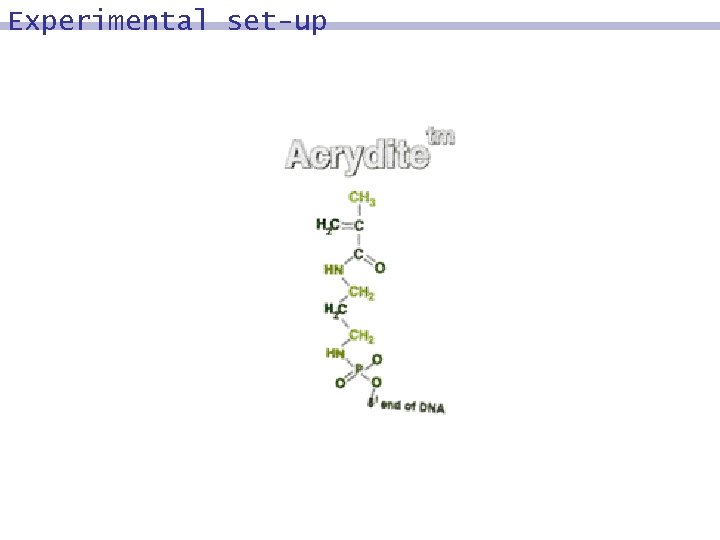 Experimental set-up
Experimental set-up
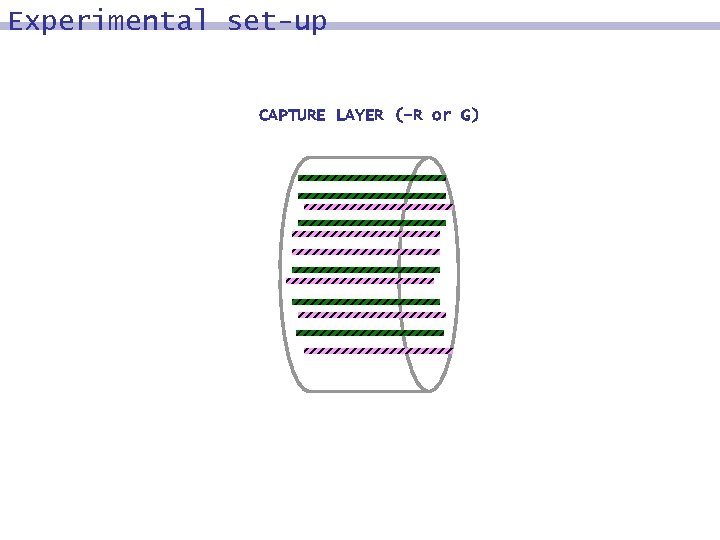 Experimental set-up CAPTURE LAYER (-R or G)
Experimental set-up CAPTURE LAYER (-R or G)
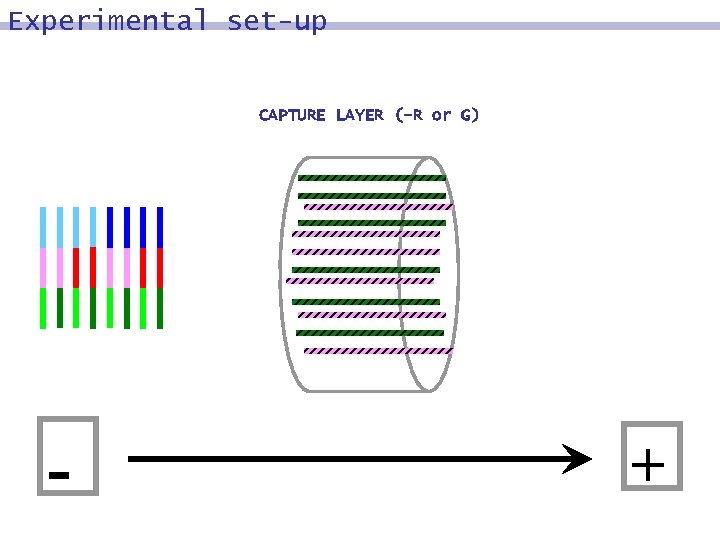 Experimental set-up CAPTURE LAYER (-R or G) - +
Experimental set-up CAPTURE LAYER (-R or G) - +
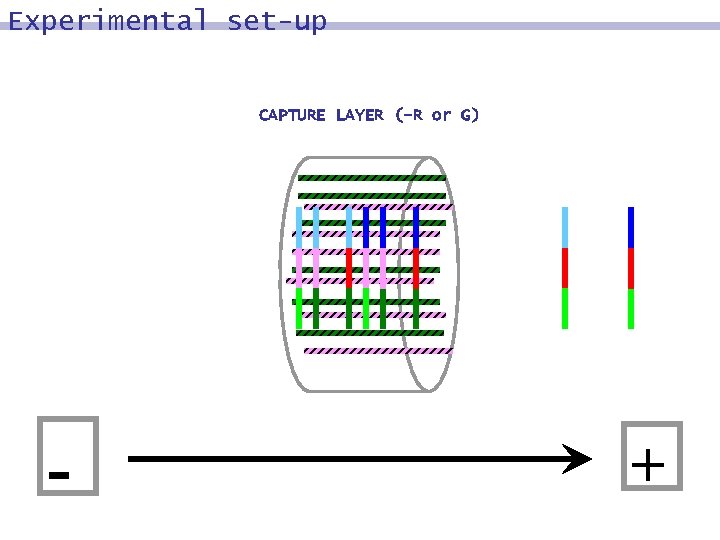 Experimental set-up CAPTURE LAYER (-R or G) - +
Experimental set-up CAPTURE LAYER (-R or G) - +
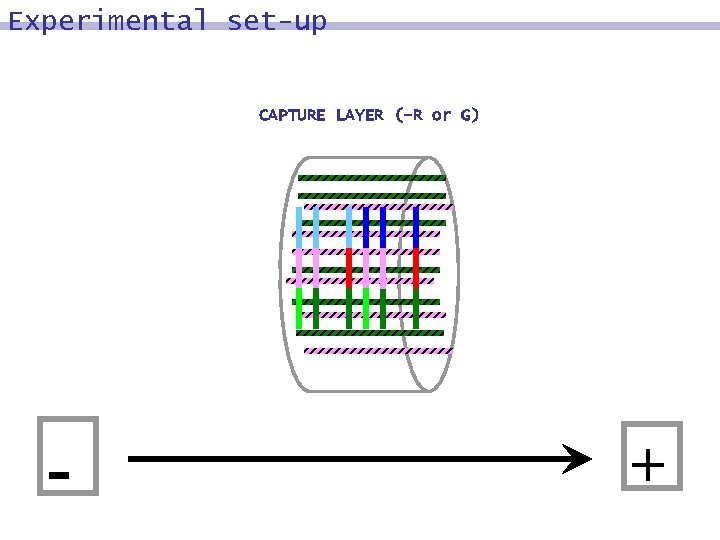 Experimental set-up CAPTURE LAYER (-R or G) - +
Experimental set-up CAPTURE LAYER (-R or G) - +
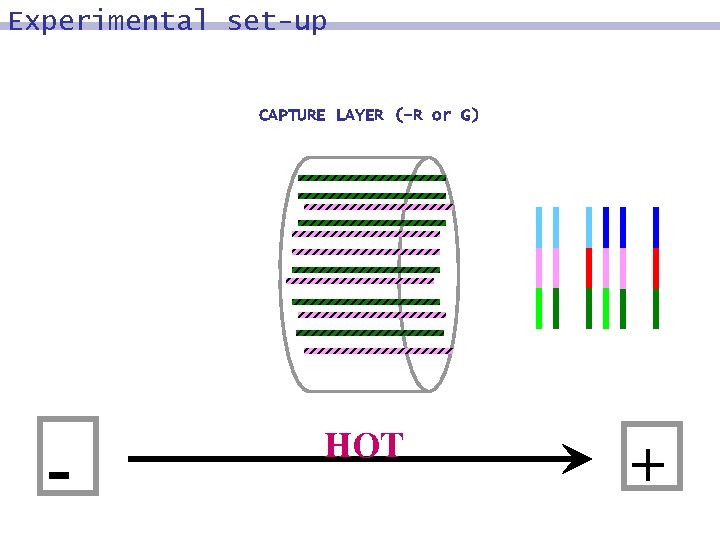 Experimental set-up CAPTURE LAYER (-R or G) - HOT +
Experimental set-up CAPTURE LAYER (-R or G) - HOT +
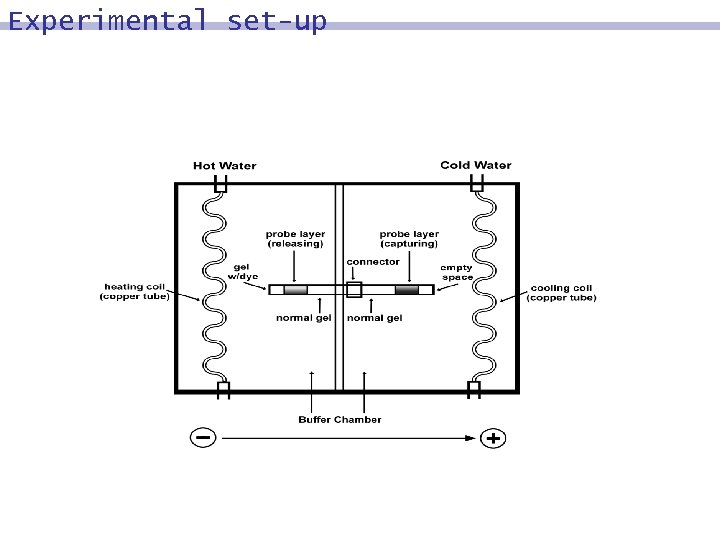 Experimental set-up
Experimental set-up
 Experimental set-up
Experimental set-up
 Experimental set-up
Experimental set-up
 DNA computing on a surface
DNA computing on a surface
 DNA computing on surfaces
DNA computing on surfaces
 DNA computing on surfaces 8 Advantages over “solution phase” chemistry 9 Facile purification steps 9 Reduced interference between strands 9 Easily automated 8 Disadvantages: 9 Loss of information density (2 D) 9 Lower surface hybridization efficiency 9 Slower surface enzyme kinetics
DNA computing on surfaces 8 Advantages over “solution phase” chemistry 9 Facile purification steps 9 Reduced interference between strands 9 Easily automated 8 Disadvantages: 9 Loss of information density (2 D) 9 Lower surface hybridization efficiency 9 Slower surface enzyme kinetics
 DNA surface model: input DNA strands representing the set {0, 1}^n are synthesized and subsequently immobilized on a surface in a non-addressed fashion
DNA surface model: input DNA strands representing the set {0, 1}^n are synthesized and subsequently immobilized on a surface in a non-addressed fashion
 Encoding binary information Word 1 2 3 4 Bit 1 2 3 4. . . A strand is comprised of words. Each word is a short DNA strand (16 mer) representing one or more bits.
Encoding binary information Word 1 2 3 4 Bit 1 2 3 4. . . A strand is comprised of words. Each word is a short DNA strand (16 mer) representing one or more bits.
 DNA word design problem 8 Requirements of a “DNA code” 9 Success in specific hybridization between a DNA code word and its Watson-crick complement 9 Few false positive signals 8 Virtually all designs enforce constraints on the code words 8 Applications: 9 Information storage, combinatorial retrieval for computing 9 Molecular bar codes for chemical libraries DNA
DNA word design problem 8 Requirements of a “DNA code” 9 Success in specific hybridization between a DNA code word and its Watson-crick complement 9 Few false positive signals 8 Virtually all designs enforce constraints on the code words 8 Applications: 9 Information storage, combinatorial retrieval for computing 9 Molecular bar codes for chemical libraries DNA
 DNA word design problem 8 Hamming: distance between two code words should be large 8 Reverse complement: distance between a word and the reverse complement another word should be large 8 of Also: frame shift, distinct sub-words, forbidden sub-words, …
DNA word design problem 8 Hamming: distance between two code words should be large 8 Reverse complement: distance between a word and the reverse complement another word should be large 8 of Also: frame shift, distinct sub-words, forbidden sub-words, …
 Work on DNA code design 8 Seeman (1990): de novo design of sequences for nucleic acid structural engineering 8 Brenner (1997): sorting polynucleotides using DNA tags 8 Shoemaker et al. (1996): analysis of yeast deletion mutants using a parallel molecular bar-coding strategy 8 Many other examples in DNA computing
Work on DNA code design 8 Seeman (1990): de novo design of sequences for nucleic acid structural engineering 8 Brenner (1997): sorting polynucleotides using DNA tags 8 Shoemaker et al. (1996): analysis of yeast deletion mutants using a parallel molecular bar-coding strategy 8 Many other examples in DNA computing
 Word design example
Word design example
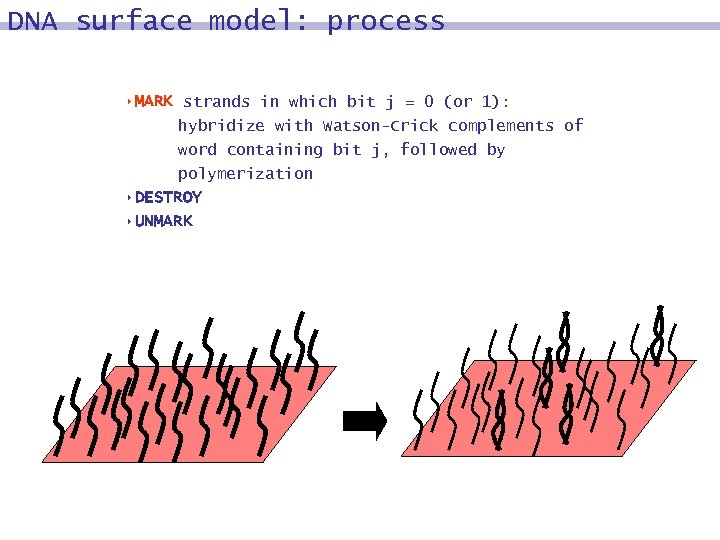 DNA surface model: process 8 MARK strands in which bit j = 0 (or 1): hybridize with Watson-Crick complements of word containing bit j, followed by polymerization 8 DESTROY 8 UNMARK
DNA surface model: process 8 MARK strands in which bit j = 0 (or 1): hybridize with Watson-Crick complements of word containing bit j, followed by polymerization 8 DESTROY 8 UNMARK
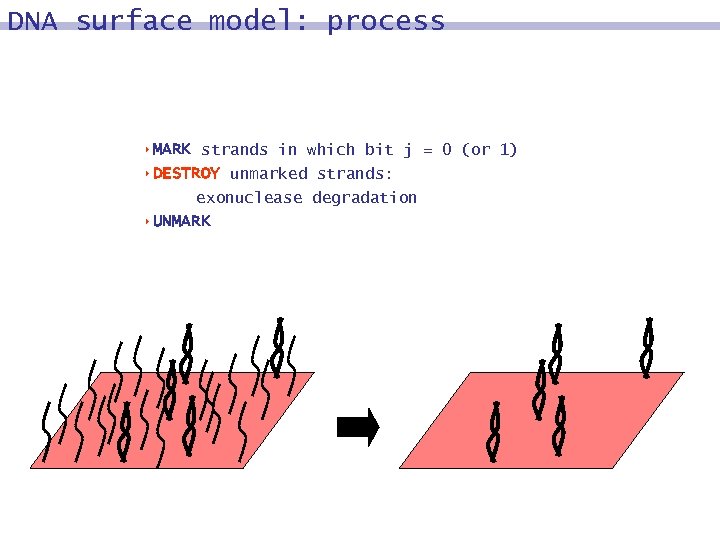 DNA surface model: process 8 MARK strands in which bit j = 0 (or 1) 8 DESTROY unmarked strands: exonuclease degradation 8 UNMARK
DNA surface model: process 8 MARK strands in which bit j = 0 (or 1) 8 DESTROY unmarked strands: exonuclease degradation 8 UNMARK
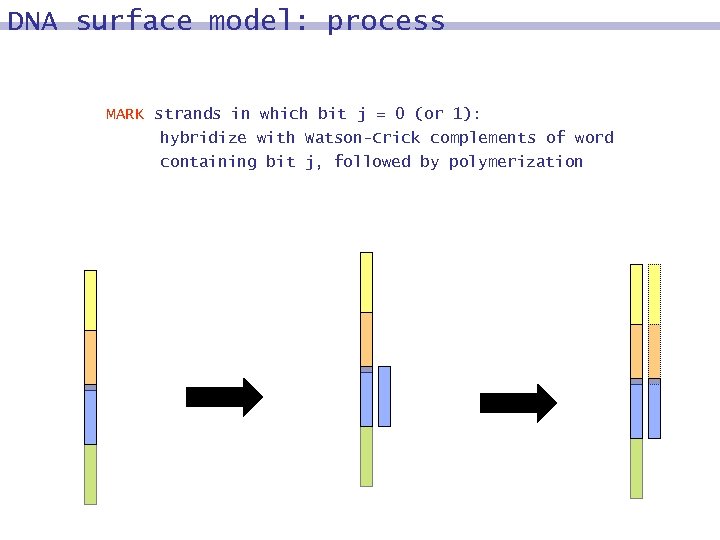 DNA surface model: process MARK strands in which bit j = 0 (or 1): hybridize with Watson-Crick complements of word containing bit j, followed by polymerization
DNA surface model: process MARK strands in which bit j = 0 (or 1): hybridize with Watson-Crick complements of word containing bit j, followed by polymerization
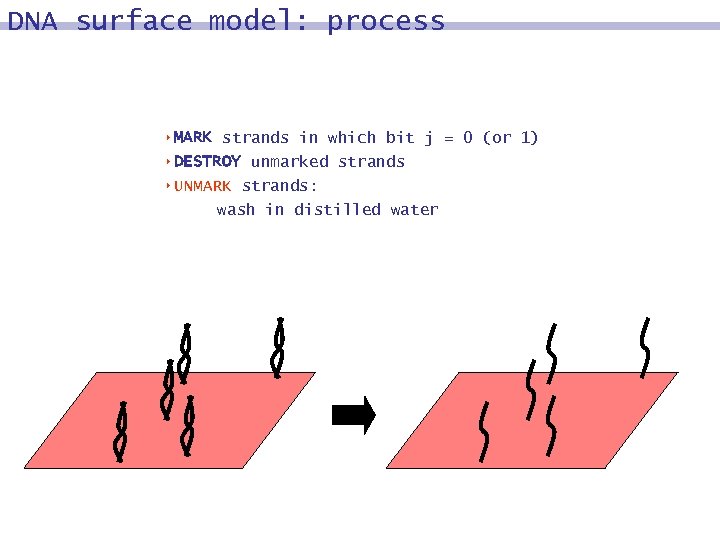 DNA surface model: process 8 MARK strands in which bit j = 0 (or 1) 8 DESTROY unmarked strands 8 UNMARK strands: wash in distilled water
DNA surface model: process 8 MARK strands in which bit j = 0 (or 1) 8 DESTROY unmarked strands 8 UNMARK strands: wash in distilled water
 DNA surface model: output Detect remaining strands (if any) by detaching strands from surface and amplifying using chain reaction). PCR (polymerase
DNA surface model: output Detect remaining strands (if any) by detaching strands from surface and amplifying using chain reaction). PCR (polymerase
 Computational power Theorem Any CNFSAT can be computed formula of size m using O(m) mark, unmark and destroy operations. Theorem Any circuit of size m can be computed using O(m) mark, unmark, destroy, and append operations.
Computational power Theorem Any CNFSAT can be computed formula of size m using O(m) mark, unmark and destroy operations. Theorem Any circuit of size m can be computed using O(m) mark, unmark, destroy, and append operations.
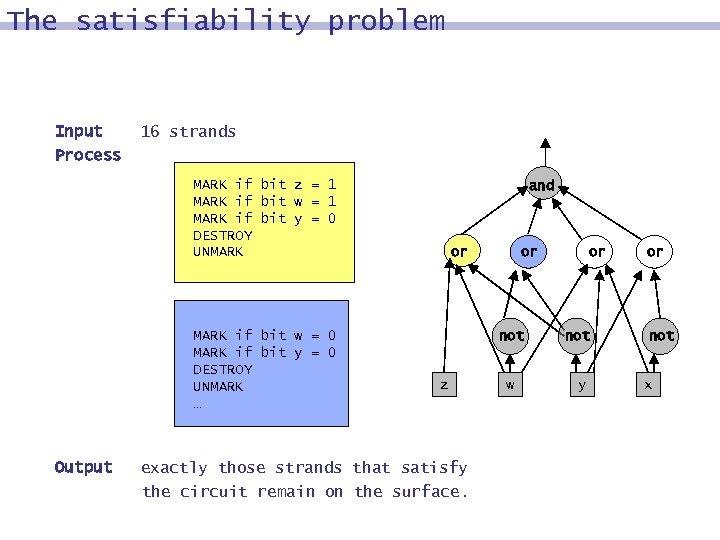 The satisfiability problem Input Process 16 strands MARK if bit z = 1 MARK if bit w = 1 MARK if bit y = 0 DESTROY UNMARK if bit w = 0 MARK if bit y = 0 DESTROY UNMARK … Output and or or not z exactly those strands that satisfy the circuit remain on the surface. w or not y or not x
The satisfiability problem Input Process 16 strands MARK if bit z = 1 MARK if bit w = 1 MARK if bit y = 0 DESTROY UNMARK if bit w = 0 MARK if bit y = 0 DESTROY UNMARK … Output and or or not z exactly those strands that satisfy the circuit remain on the surface. w or not y or not x
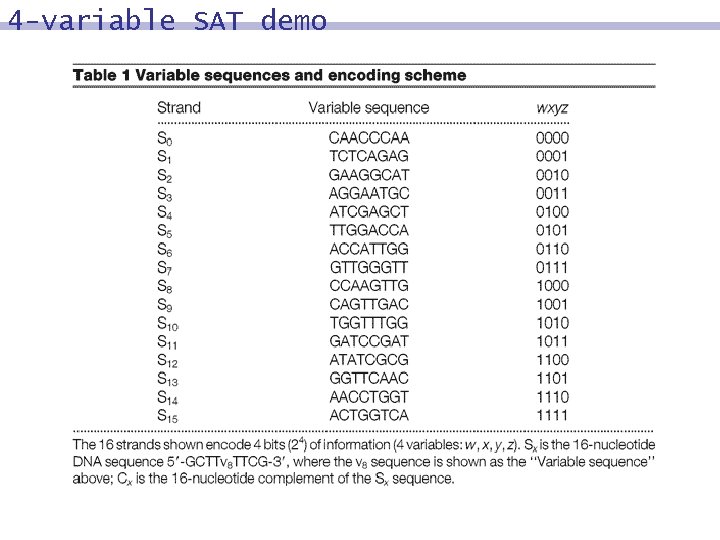
 4 -variable SAT demo (w x y) (w y z) ( x y) ( w y) {0000} {0010} {0100} {0110} {1000} {1010} {1100} {1110} {0001} {0011} {0101} {0111} {1001} {1011} {1101} {1111}
4 -variable SAT demo (w x y) (w y z) ( x y) ( w y) {0000} {0010} {0100} {0110} {1000} {1010} {1100} {1110} {0001} {0011} {0101} {0111} {1001} {1011} {1101} {1111}
 4 -variable SAT demo
4 -variable SAT demo
 4 -variable SAT demo
4 -variable SAT demo
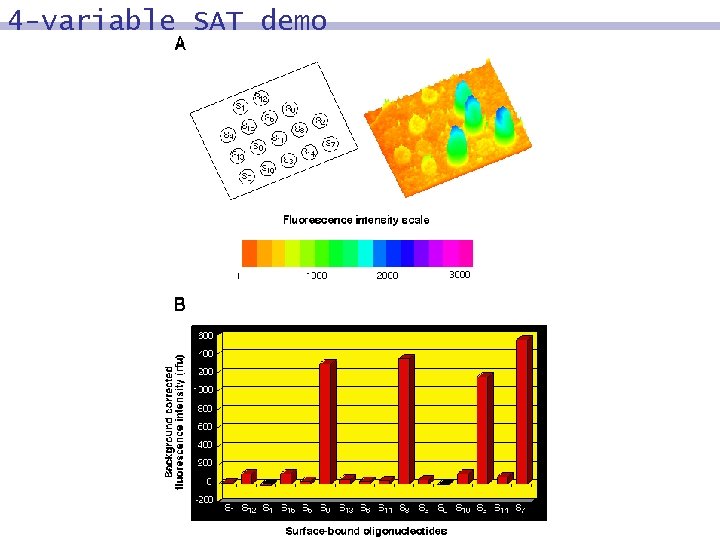
 4 -variable SAT demo 8 The logic computation of the DNA in each cycle, leading at the end to four types of DNA molecules remaining on the surface. 8 The identity of those molecules that correspond to the solutions was determined by PCR. 8 Solution: S 3 S 7 S 8 S 9
4 -variable SAT demo 8 The logic computation of the DNA in each cycle, leading at the end to four types of DNA molecules remaining on the surface. 8 The identity of those molecules that correspond to the solutions was determined by PCR. 8 Solution: S 3 S 7 S 8 S 9
 4 -variable SAT, the answers S 3: w=0, x=0, y=1, z=1 S 7: w=0, x=1, y=1, z=1 S 8: w=1, x=0, y=0, z=0 S 9: w=1, x=0, y=0, z=1 y=1: ( w V x V y) z=1: ( w V y V z) x=0 or y=1: (x V y) w=0: (w V y)
4 -variable SAT, the answers S 3: w=0, x=0, y=1, z=1 S 7: w=0, x=1, y=1, z=1 S 8: w=1, x=0, y=0, z=0 S 9: w=1, x=0, y=0, z=1 y=1: ( w V x V y) z=1: ( w V y V z) x=0 or y=1: (x V y) w=0: (w V y)
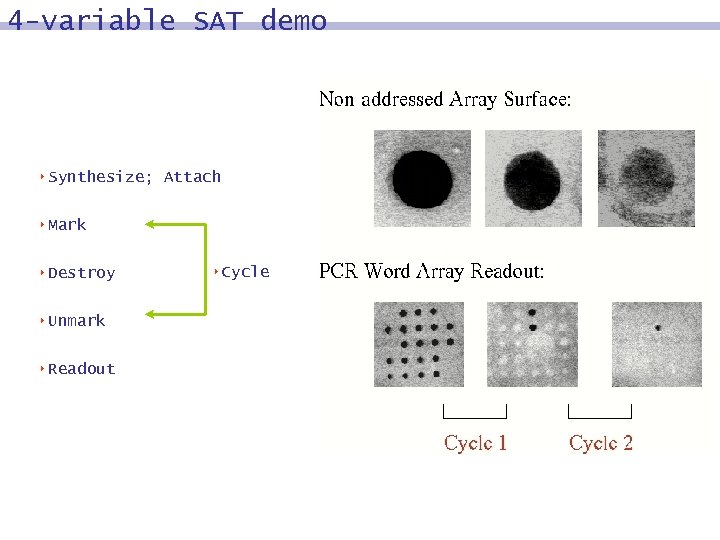 4 -variable SAT demo 8 Synthesize; Attach 8 Mark 8 Destroy 8 Unmark 8 Readout 8 Cycle
4 -variable SAT demo 8 Synthesize; Attach 8 Mark 8 Destroy 8 Unmark 8 Readout 8 Cycle
 4 -variable SAT demo
4 -variable SAT demo
 Conclusions 8 Solid-phase chemistry is a promising approach to DNA computing 8 DNA computing will require greatly improved DNA surface attachment chemistries and control of chemical and enzymatic processes
Conclusions 8 Solid-phase chemistry is a promising approach to DNA computing 8 DNA computing will require greatly improved DNA surface attachment chemistries and control of chemical and enzymatic processes


