Adjoint modeling and applications Consider a forward model

Adjoint modeling and applications Consider a forward model y = F(x) with Jacobian matrix The adjoint of that forward model applies KT to vectors called adjoint forcings This is useful for • Determining the sensitivity of model output to model variables going back in time; • Solving the inverse problem numerically rather than analytically to accommodate large state vectors (4 DVAR inversion)

Adjoint model as sensitivity analysis tool Forward model (CTM): State vector Concentrations Time x(0) y(0) t 0 y(1) t 1 y(p-1) tp-1 y(p) tp Jacobian expresses sensitivity of y(p) to x(0): Take transpose: Apply sequentially to unit vector v = (1, 0… 0)T: followed by etc… Single pass of the adjoint over [tp, t 0] returns sensitivity of y(p), 1 to all model variables at all previous times: y(p), 1/ y(p-1), y(p), 1/ y(p-2), … y(p), 1/ x(0)

Application to receptor modeling: sensitivity of smoke in Singapore to fire locations in Equatorial Asia MODIS fire observations, June 20 -29 2013 Smoke in Singapore, June 20 Smoke transport simulated by GEOS-Chem • Large fire emissions in Equatorial Asia from oil palm and timber plantations • Adjoint can identify the sensitivity of smoke concentrations at a particular receptor site to fire emissions at all locations and previous times Smoke concentration in surface air Kim et al. [2015]

Using GEOS-Chem adjoint to compute sensitivity of smoke concentrations in Singapore to fire emissions E(x, t) from bottom-up inventory Concentrations y(x, t) =F(E(x, t)) computed with GEOS-Chem Sensitivities s (x, t, t’) = y. Singapore(t)/ E(x, t’) computed with GEOS-Chem adjoint Contributions to Singapore smoke Smoke concentrations in Singapore can be calculated for ANY emission inventory E and time t using archived sensitivities computed just ONCE from the adjoint:

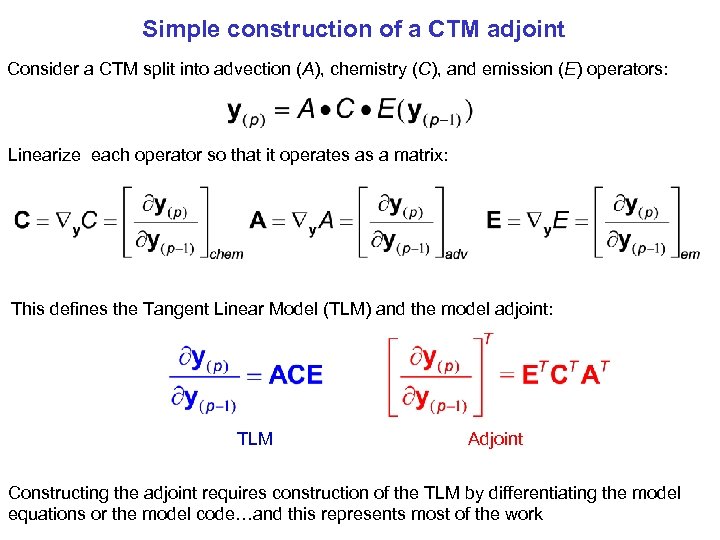Simple construction of a CTM adjoint Consider a CTM split into advection (A), chemistry (C), and emission (E) operators: Linearize each operator so that it operates as a matrix: This defines the Tangent Linear Model (TLM) and the model adjoint: TLM Adjoint Constructing the adjoint requires construction of the TLM by differentiating the model equations or the model code…and this represents most of the work

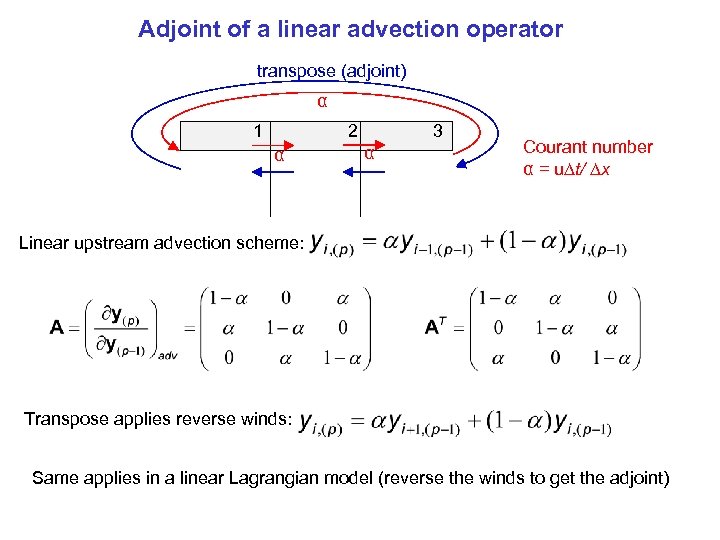Adjoint of a linear advection operator transpose (adjoint) α 1 2 α 3 α Courant number α = u t/ x Linear upstream advection scheme: Transpose applies reverse winds: Same applies in a linear Lagrangian model (reverse the winds to get the adjoint)

Adjoint of a linear chemistry operator A linear chemistry operator is self-adjoint; same operator can be used in forward and adjoint models. Sensitivity with respect to emissions is also self-adjoint:

Variational inversion A x. A 1 Solve the inverse problem ° 2 ° 1 x numerically rather than analytically x 2° 1. Starting from prior x. A , calculate 3 x 3 ° 2. Using a steepest-descent algorithm get next guess x 1 3. Calculate , get next guess x 2 4. Iterate until convergence Adjoint model computes by applying KT to adjoint forcings Minimum of cost function J

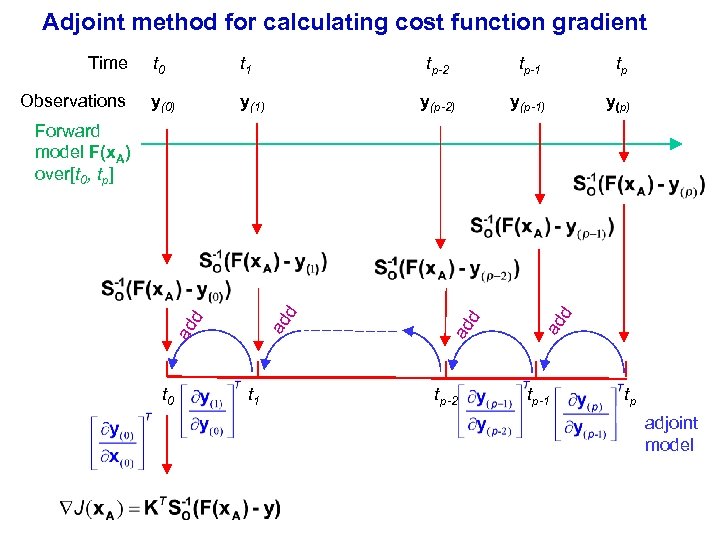Adjoint method for calculating cost function gradient Time Observations t 0 t 1 tp-2 y(0) y(1) tp-1 tp y(p-2) y(p-1) y(p) t 0 t 1 tp-2 d ad ad ad d d Forward model F(x. A) over[t 0, tp] tp-1 tp adjoint model

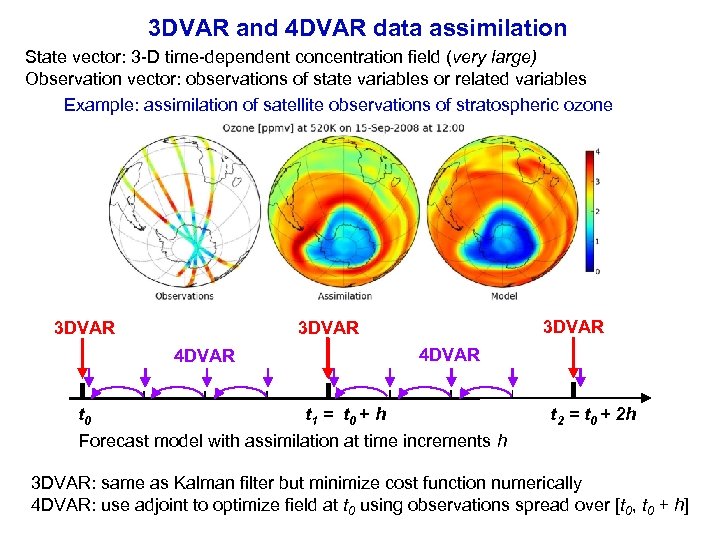3 DVAR and 4 DVAR data assimilation State vector: 3 -D time-dependent concentration field (very large) Observation vector: observations of state variables or related variables Example: assimilation of satellite observations of stratospheric ozone 3 DVAR 4 DVAR t 0 t 1 = t 0 + h Forecast model with assimilation at time increments h t 2 = t 0 + 2 h 3 DVAR: same as Kalman filter but minimize cost function numerically 4 DVAR: use adjoint to optimize field at t 0 using observations spread over [t 0, t 0 + h]