Aditya Bhaskara Princeton Moses Charikar Princeton Venkatesan Guruswami

Зарегистрируйтесь, чтобы просмотреть полный документ!

Aditya Bhaskara (Princeton) Moses Charikar (Princeton) Venkatesan Guruswami (CMU) Aravindan Vijayaraghavan (Princeton) Yuan Zhou (CMU)

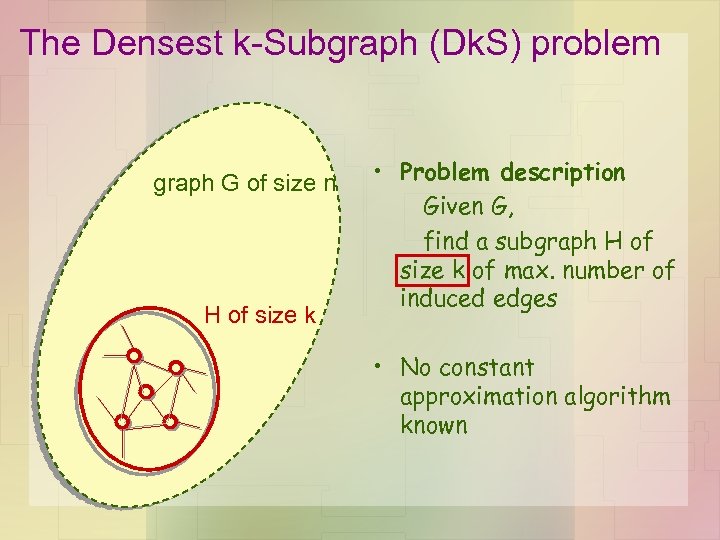
The Densest k-Subgraph (Dk. S) problem graph G of size n H of size k • Problem description Given G, find a subgraph H of size k of max. number of induced edges • No constant approximation algorithm known

Related problems • Max-density subgraph – no size restriction for the subgraph – find a subgraph of max. edge density (i. e. average degree) – solvable in poly-time [GGT'87]

Algorithmic applications • Social networks. Trawling the web for emerging cybercommunities [KRRT '99] – Web communities are characterized by dense bipartite subgraphs • Computational biology. Mining dense subgraphs across massive biological networks for functional discovery [HYHHZ '05] – Dense protein interaction subgraph corresponds to a protein complex [BD '03]

Hardness applications • Best approximation algorithm: ratio [BCCFV '10] approximation • Mostly used as an (average case) hardness assumption – [ABW '10] Variant was used as the hardness assumption in Public Key Cryptography – [ABBG '10] Toxic assets can be hidden in complex financial derivatives to commit undetectable fraud – [CMVZ '12] Derive inapproximability for many other problems (e. g. k-route cut)

Proof of hardness? • Unfortunately, APX-hardness is not known for the Densest k-subgraph problem

Evidence of hardness? • [Feige '02] No PTAS under the Random 3 -SAT hypothesis • [Khot '04] No PTAS unless • [RS '10] No constant factor approximation assuming the Small Set Expansion Conjecture • [FS '97] Natural SDP has an integrality gap – Doesn't serve as a "strong" evidence since stronger SDP indeed improves the integrality gap [BCCFV '10]

Our results • Polynomial integrality gaps for strong SDP relaxation hierarchies • Theorem. gap for SA+ (Sherali-Adams+ SDP) hierarchy • Theorem. hierarchy gap for levels of Lasserre levels of

Implications of the SA+ SDP gap • Beating the best known approximation factor is a barrier for current techniques – Since the algorithm of [BCCFV '10] only uses constant rounds of Sherali-Adams LP relaxation • Natural distributions of instances are gap instances w. h. p. – We use Erdös-Renyi random graphs as gap instances

Implications of the Lasserre SDP gap • A strong (and first) evidence that Dk. S is hard to approximate within polynomial factors – Reason: Very few problems have Lasserre gaps stronger than known NP-Hardness results NP-Hardness Lasserre Gap Max K-CSP [EH 05] [Tul 09] K-Coloring [KP 06] [Tul 09] Balanced Seperator, Uniform Sparest Cut 1 [GSZ'11] Dk. S 1 this work

Lasserre SDP gap for Dk. S

Outline • Gap reduction from [Tulsiani '09] (linear round Lasserre gap for Max K-CSP) gap instance for Max K-CSP SDP gap instance for Dk. S SDP – Vector completeness: perfect solution for good solution for Max K-CSP SDP Dk. S SDP – Soundness: there is no good integer solution (w. h. p. )

The bipartite version of Dk. S • The Dense (k 1, k 2)-subgraph problem. – Given bipartite graph G = (V, W, E) – Find two subsets , such that 1) 2) (# of induced edges) is maximized • Lemma. Lasserre gap of Dense (k 1, k 2)-subgraph problem implies Lasserre gap of Dk. S • Only need to show Lasserre gap of Dense (k 1, k 2)subgraph problem

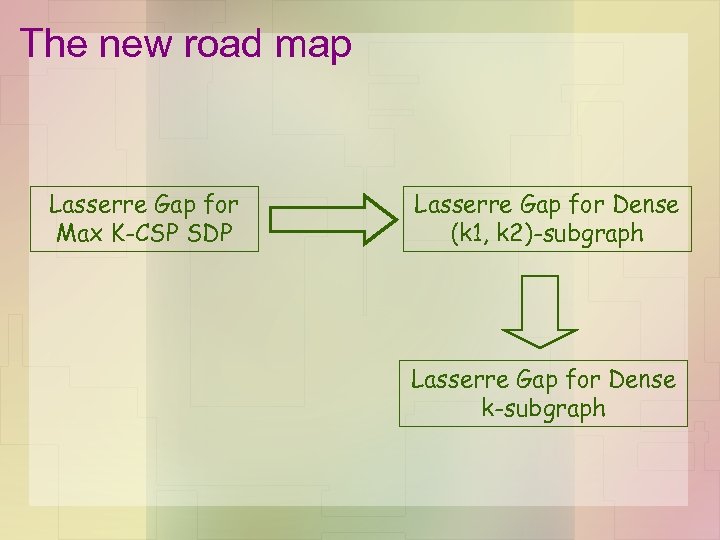
The new road map Lasserre Gap for Max K-CSP SDP Lasserre Gap for Dense (k 1, k 2)-subgraph Lasserre Gap for Dense k-subgraph

The Max K-CSP instance • A linear code: • Alphabet: [q] = {0, 1, 2, . . . , q-1} • Variables: • Constraints: – is over , insisting – where • A random Max K-CSP instance: – Choose and completely by random

Integrality gap for Max K-CSP [Tul 09] • Given C as a dual code of dist >= 3, for a random Max KCSP instance • Vector completeness. For constant K, there exists perfect solution for linear round Lasserre SDP w. h. p. • Soundness. W. h. p. no solution satisfies more than (fraction) clauses.

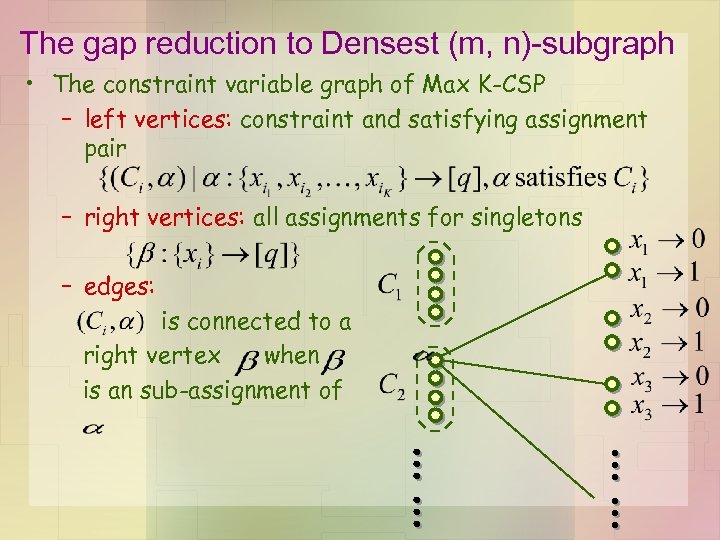
The gap reduction to Densest (m, n)-subgraph • The constraint variable graph of Max K-CSP – left vertices: constraint and satisfying assignment pair – right vertices: all assignments for singletons – edges: is connected to a right vertex when is an sub-assignment of

Integrality gap • Vector Completeness. Max K-CSP instance is perfect satisfiable (in Lasserre) Dense (m, n)Subgraph (in Lasserre) – Intuition: translate the following argument (for integer solution) into Lasserre language – Given an satisfying solution for Max K-CSP instance, we can choose m left vertices (one per constraint) and n right vertices (one per variable) agree with the solution, such that the subgraph is "dense"

Integrality gap (cont'd) • Vector Completeness. Max K-CSP instance is perfect satisfiable (in Lasserre) Dense (m, n)Subgraph (in Lasserre) • Soundness. W. h. p. there is no dense (m, n)-subgraph – Intuition: random bipartite graph does not have dense (m, n)-subgraph w. h. p. – Argue that our graph has enough randomness to rule out dense (m, n)-subgraph

Parameter selection • Take – C as the dual of Hamming code (i. e. the Hadamard code) – , Get gap for -round Lasserre SDP • Take – C as some generalized BCH code – carefully chosen q and K Get gap for -round Lasserre SDP

Furture directions • gap for -round Lasserre SDP ? • gap for -round Sherali-Adams+ SDP ?

Thank you!

Скачать презентацию Aditya Bhaskara Princeton Moses Charikar Princeton Venkatesan Guruswami

5a79b4e9e2bee5079dffc9f9d2cc21bb.ppt

Количество слайдов: 22