3745de298cf596599cf9d78d092d723f.ppt
- Количество слайдов: 32

Adaptive GPU Cache Bypassing Yingying Tian* , Sooraj Puthoor†, Joseph L. Greathouse†, Bradford M. Beckmann†, Daniel A. Jiménez* Texas A&M University*, AMD Research†

Outline • Background and Motivation • Adaptive GPU Cache bypassing • Methodology • Evaluation Results • Case Study of Programmability • Conclusion

Graphics Processing Units (GPUs) • Tremendous throughput • High performance computing • Target for general-purpose GPU computing – Programming model: CUDA, Open. CL – Hardware support: cache hierarchies – AMD GCN: 16 KB L 1, NVIDIA Fermi: 16 KB/48 KB configurable

Inefficiency of GPU Caches • Thousands of concurrent threads – Low per-thread cache capacity • Characteristics of GPU workloads – Large data structures – Useless insertion consumes energy – Reducing the performance by replacing useful blocks • Scratchpad memories filter temporal locality – Less reuse caught in caches – Limit programmability

Memory Characteristics n m ea nw h. ar it t so r t dc c ni bi to nn m lud at rix m u km l ea ns hi st og ra ba m ck pr op s bf sr ad 100% 90% 80% 70% 60% 50% 40% 30% 20% 10% 0% sp m v Dynamically Accessed Cache Blocks • Zero-reuse blocks: inserted into caches without being accessed again until evicted • 46% (max. 84%) of L 1 cache blocks are only accessed once before eviction • Consume energy; pollute cache; cause more replacement

Motivation • GPU caches are inefficient • Increasing cache sizes is impractical • Inserting zero-reuse blocks wastes power without performance gain • Inserting zero-reuse blocks causes useful blocks being replaced to reduce performance Objective: Bypass zero-reuse blocks

Outline • Background and Motivation • Adaptive GPU Cache bypassing • Methodology • Evaluation Results • Case Study of Programmability • Conclusion
![Bypass Zero-Reuse Blocks • Static bypassing on resource limit [Jia et. al 2014] – Bypass Zero-Reuse Blocks • Static bypassing on resource limit [Jia et. al 2014] –](https://present5.com/presentation/3745de298cf596599cf9d78d092d723f/image-8.jpg)
Bypass Zero-Reuse Blocks • Static bypassing on resource limit [Jia et. al 2014] – Degrade the performance • Dynamic bypassing – Adaptively bypass zero-reuse blocks – Make prediction on cache misses – What information shall we use to make prediction? • • Memory addresses Memory instructions

so nw rt sp m v ge sra om d ea n ck pr o p bf bi s to ni c hi d st ct og r km am ea ns m lu at d rix m ul nn 120 110 100 90 80 70 60 50 40 30 20 10 0 ba nw so rt sp m v ge srad om ea n pr ck ba • • • b bi fs to ni c hi d st ct og ra km m ea ns m lu at d rix m ul nn Distinct PCs with Load Instructions 900000 800000 700000 600000 500000 400000 300000 200000 100000 0 op Distinct Cache Blocks Accessed Memory Address vs. PC Using memory addresses is impractical due to storage Using memory instructions consumes far less overhead PCs generalize the behaviors of SIMD with high accuracy

Adaptive GPU Cache Bypassing PC-based dynamic Bypass Predictor • Inspired by dead block prediction in CPU caches [Lai et. al 2001][Khan et. al 2010] - If a PC leads to the last access to one block, then the same PC will lead to the last access to other blocks • On cache misses, predict if it is zero-reuse - If yes, requested block will bypass the cache • On cache hits, verify previous prediction and make new prediction
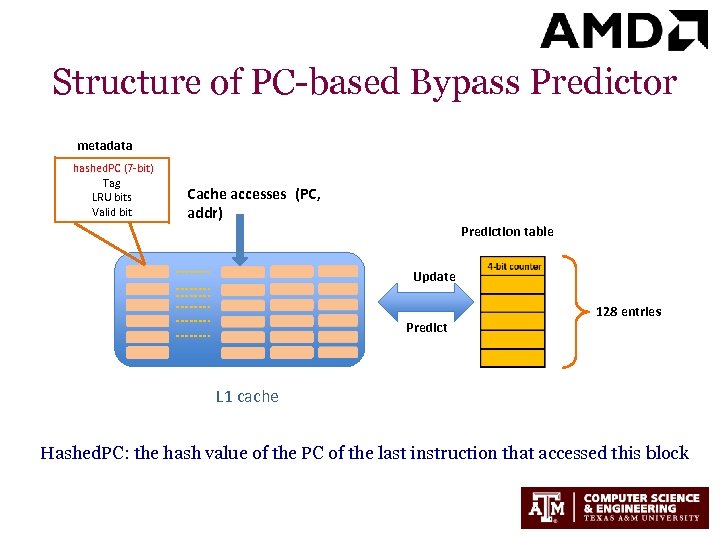
Structure of PC-based Bypass Predictor metadata hashed. PC (7 -bit) Tag LRU bits Valid bit Cache accesses (PC, addr) Prediction table Update Predict 128 entries L 1 cache Hashed. PC: the hash value of the PC of the last instruction that accessed this block
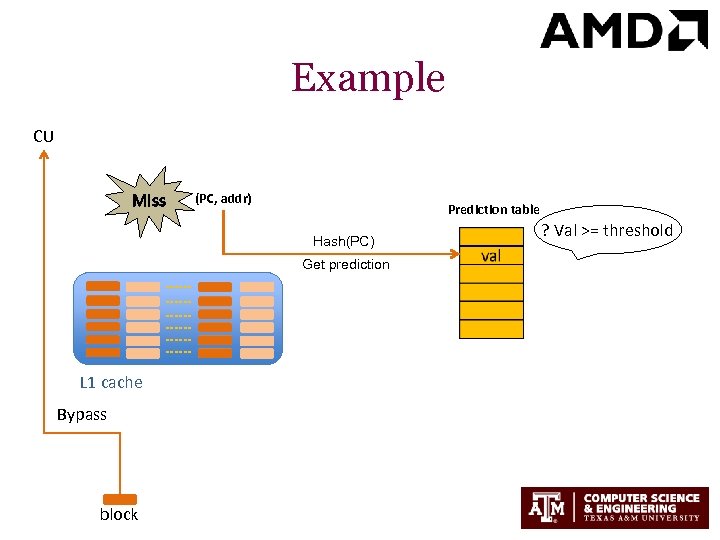
Example CU Miss (PC, addr) Prediction table Hash(PC) Get prediction L 1 cache Bypass block ? Val >= threshold
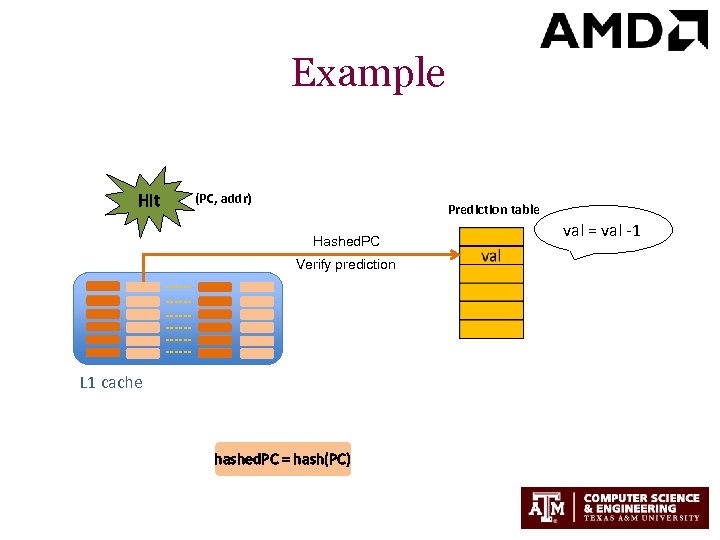
Example Hit (PC, addr) Prediction table Hashed. PC Verify prediction L 1 cache hashed. PC = hash(PC) val = val -1
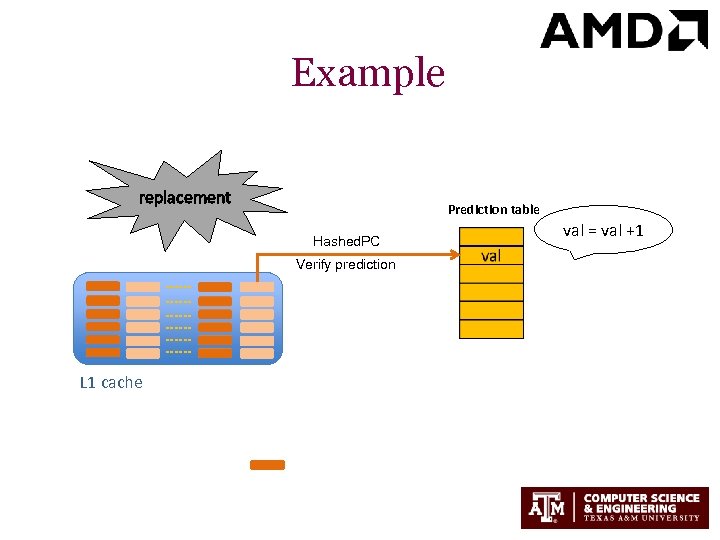
Example replacement Prediction table Hashed. PC Verify prediction L 1 cache val = val +1

Misprediction Correction • • Bypass misprediction is irreversible Cause additional penalties to access lower level caches Utilize this procedure to help verify misprediction Each L 2 entry contains an extra bit: Bypass. Bit – Bypass. Bit == 1 if the requested block will bypass L 1 – Intuition: if it is a bypass misprediction, this block should be rereferenced soon, and will be hit in the L 2 cache • Miscellaneous – Set dueling – Sampling

Outline • Background and Motivation • Adaptive GPU Cache bypassing • Methodology • Evaluation Results • Case Study of Programmability • Conclusion

Methodology • In-house APU simulator that extends Gem 5 - Similar to AMD Graphics Core Next architecture • Benchmarks: Rodinia, AMD APP SDK, Open. Dwarfs GPU cache configuration CUs 8, 1 GHz, 64 scalar units by 4 SIMDs L 1 cache 8 -way, 16 KB, 1 -cycle tag, 4 -cycle data access Shared L 2 cache 16 -way, 256 KB, 4 -cycle tag, 16 -cycle data access Shared L 3 cache 16 -way, 4 MB, 15 -cycle tag, 30 -cycle data access

Storage Overhead • Evaluated Techniques PC-based bypass predictor Prediction table/L 1 cache 4 -bit * 128 entries Metadata/L 1 block 7 bits Metadata/L 2 block 1 bit Total cost 224 bytes out of 16 KB L 1 (1. 5%) 0. 5 KB out of 256 KB L 2 (0. 2%) Counter-based bypass predictor Prediction table/L 1 cache 128* 128 entries, 5 -bits Metadata/L 1 block 20 bits (hashed. PC, counters, prediction) Total cost 10. 625 KB out of 16 KB L 1 (66. 4%)

Outline • Background and Motivation • Adaptive GPU Cache bypassing • Methodology • Evaluation Results • Case Study of Programmability • Conclusion
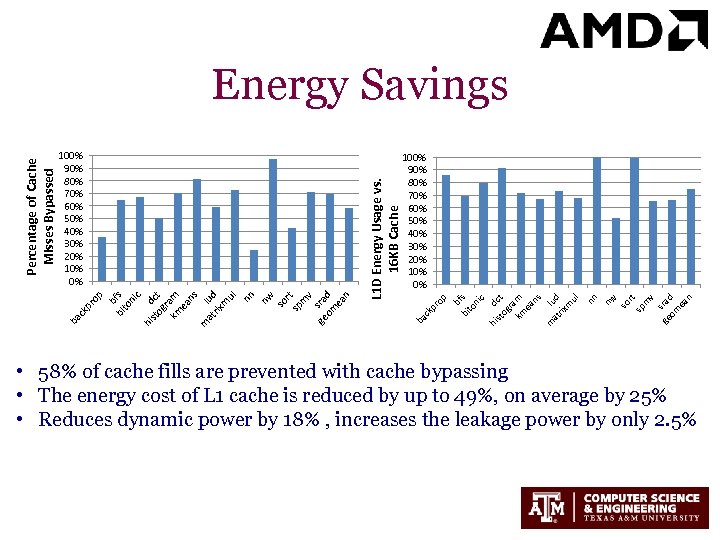
so rt sp m v sr ge ad om ea n nw b bi fs to ni c hi dc st og t ra km m ea ns m lu at d rix m ul nn op pr ck L 1 D Energy Usage vs. 16 KB Cache 100% 90% 80% 70% 60% 50% 40% 30% 20% 10% 0% ba ck ba nw so r sp t m v ge sra om d ea n op b bi fs to ni c hi d st ct og r km am ea ns m lu at d rix m ul nn 100% 90% 80% 70% 60% 50% 40% 30% 20% 10% 0% pr Percentage of Cache Misses Bypassed Energy Savings • 58% of cache fills are prevented with cache bypassing • The energy cost of L 1 cache is reduced by up to 49%, on average by 25% • Reduces dynamic power by 18% , increases the leakage power by only 2. 5%
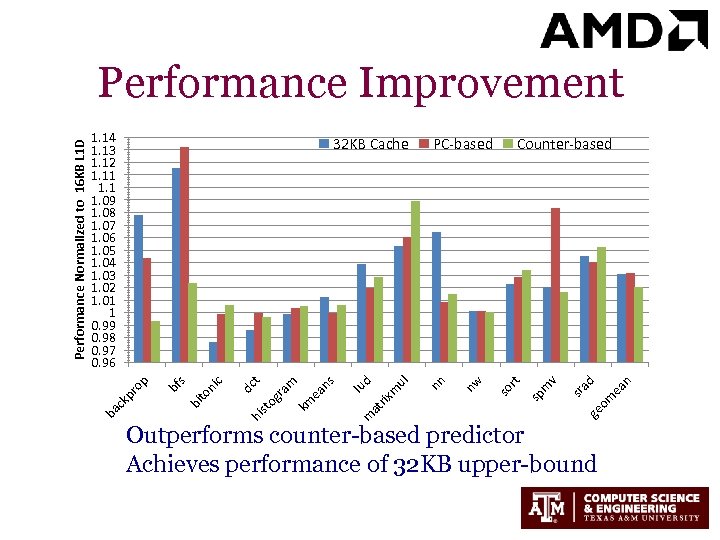
n ea om ad ge sr sp m so v Counter-based rt PC-based nw ul m at rix lu d m ns ea m km t og ra dc hi st to ni c s bf bi ck pr op 32 KB Cache nn 1. 14 1. 13 1. 12 1. 11 1. 09 1. 08 1. 07 1. 06 1. 05 1. 04 1. 03 1. 02 1. 01 1 0. 99 0. 98 0. 97 0. 96 ba Performance Normalized to 16 KB L 1 D Performance Improvement Outperforms counter-based predictor Achieves performance of 32 KB upper-bound
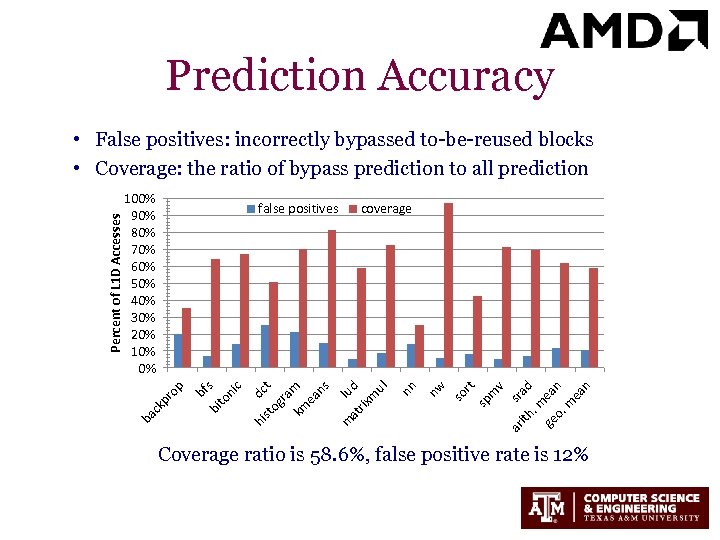
Prediction Accuracy a. m d ge ea o. n m ea n sr ith t sp m so r v ar at lu d rix m ul nn coverage m og t ra km m ea ns dc hi st c s to ni bf bi ck pr op false positives nw 100% 90% 80% 70% 60% 50% 40% 30% 20% 10% 0% ba Percent of L 1 D Accesses • False positives: incorrectly bypassed to-be-reused blocks • Coverage: the ratio of bypass prediction to all prediction Coverage ratio is 58. 6%, false positive rate is 12%

Outline • Background and Motivation • Adaptive GPU Cache bypassing • Methodology • Evaluation Results • Case Study of Programmability • Conclusion

Scratchpad Memories vs. Caches • • Store reused data shared within a compute unit Programmer-managed vs. hardware-controlled Scratchpad memories filter out temporal locality Limited programmability – Explicitly remapping from memory address space to the scratchpad address space To what extent can L 1 cache bypassing make up for the performance loss caused by removing scratchpad memories?

Case Study: Needleman-Wunsch (nw) • nw: – Global optimization algorithm – Compute-sensitive – Very little reuse observed in L 1 caches • Rewrote nw to remove the use of scratchpad memories: nw-no. SPM – Not simply replace _local_ functions with _global_ functions – Best-effort re-written version
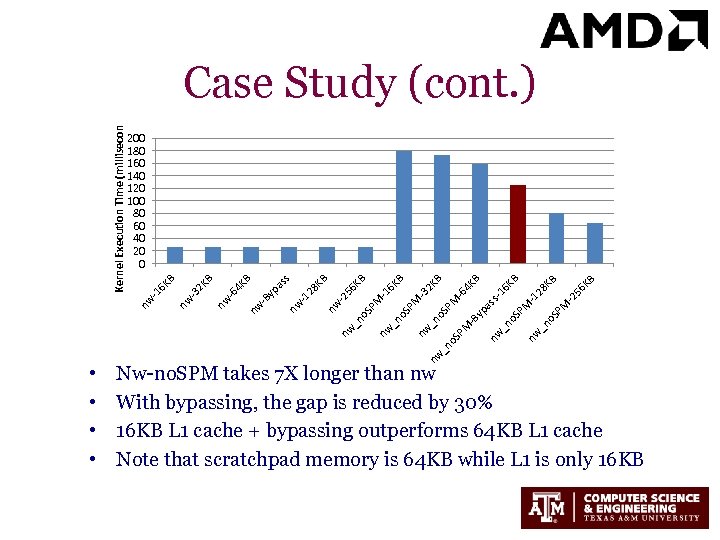
• • KB nw _n o. S PM -2 28 -1 56 KB B PM o. S _n nw M -B y pa ss -1 6 K B 4 K -6 nw _n o SP nw _n o. S PM o. S _n nw PM -3 2 6 K -1 PM o. S _n nw KB B KB 56 -2 nw -1 28 KB s nw nw -B yp as B 4 K B nw -6 2 K nw -3 6 K B 200 180 160 140 120 100 80 60 40 20 0 nw -1 Kernel Execution Time (milliseconds) Case Study (cont. ) Nw-no. SPM takes 7 X longer than nw With bypassing, the gap is reduced by 30% 16 KB L 1 cache + bypassing outperforms 64 KB L 1 cache Note that scratchpad memory is 64 KB while L 1 is only 16 KB

Conclusion • GPU caches are inefficient • We propose a simple but effective GPU cache bypassing technique • Improves GPU cache efficiency • Reduces energy overhead • Requires far less storage overhead • Bypassing allows us to move towards more programmable GPUs

Thank you! Questions?
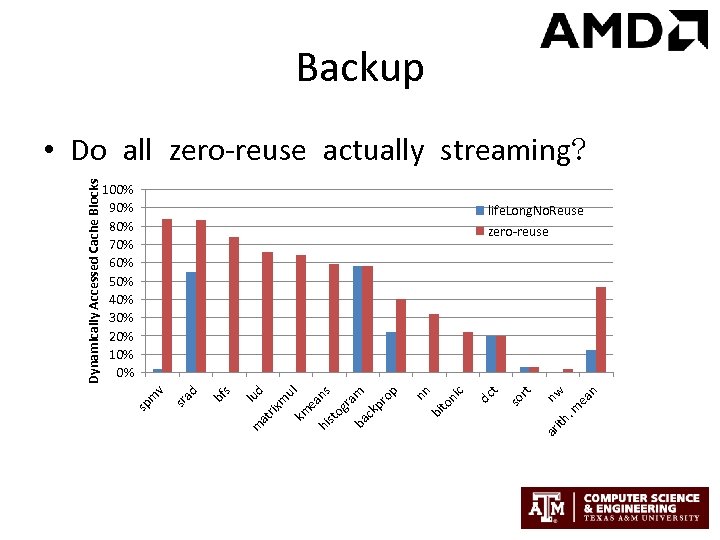
n nw ea . m ith ar t so r t 100% 90% 80% 70% 60% 50% 40% 30% 20% 10% 0% dc c nn to ni bi m ns ul pr op ck ba ea og ra st hi km lu d m rix at m s bf ad sr v sp m Dynamically Accessed Cache Blocks Backup • Do all zero-reuse actually streaming? life. Long. No. Reuse zero-reuse
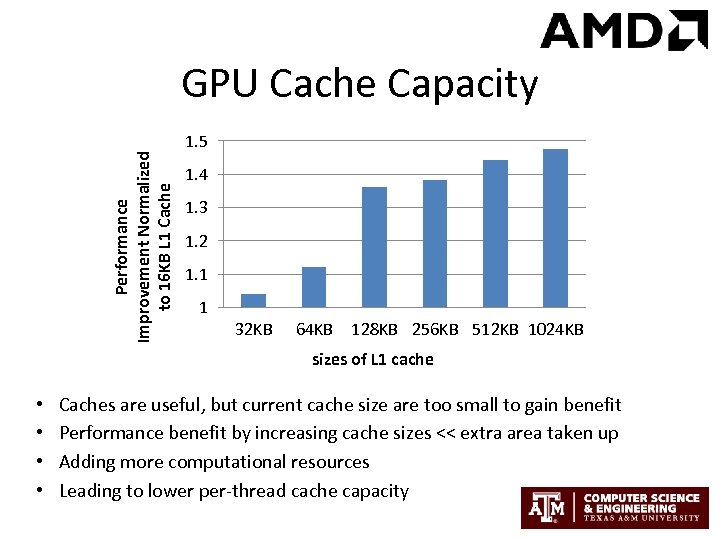
Performance Improvement Normalized to 16 KB L 1 Cache GPU Cache Capacity 1. 5 1. 4 1. 3 1. 2 1. 1 1 32 KB 64 KB 128 KB 256 KB 512 KB 1024 KB sizes of L 1 cache • • Caches are useful, but current cache size are too small to gain benefit Performance benefit by increasing cache sizes << extra area taken up Adding more computational resources Leading to lower per-thread cache capacity
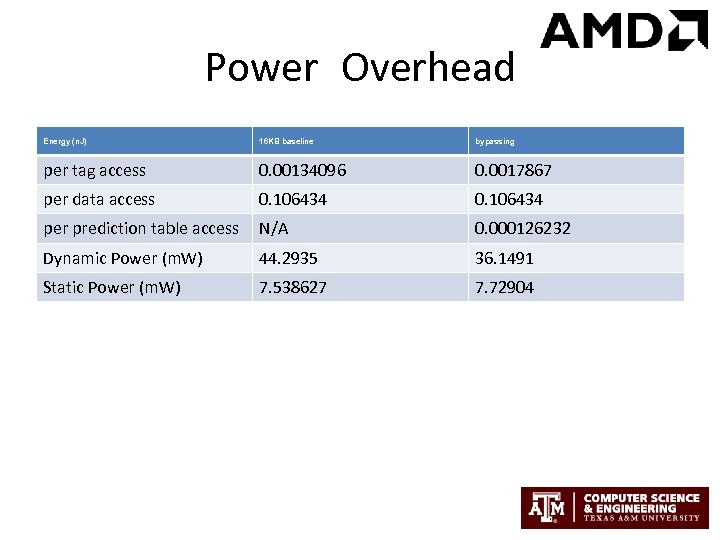
Power Overhead Energy (n. J) 16 KB baseline bypassing per tag access 0. 00134096 0. 0017867 per data access 0. 106434 per prediction table access N/A 0. 000126232 Dynamic Power (m. W) 44. 2935 36. 1491 Static Power (m. W) 7. 538627 7. 72904

Compare with SDBP • SDBP is designed for LLCs, where much of the temporal locality has been filtered • our technique is designed for GPU L 1 caches, where temporal information is complete. We use PCs because of the observation of characteristics of GPGPU memory accesses. • GPU kernels are small and frequently launched, the interleaving changes frequently.
3745de298cf596599cf9d78d092d723f.ppt