ACM today The Fall competition is getting organized

ACM today The Fall competition is getting organized… it's going to be lonely…

Mock mock contest #2 More teams solved problems; more problems were solved All problems solved by some team shipping all-pairs shortest paths could be used for this one… Still one computer per team… API-reference is OK on another machine forward following calls through a graph of forwarding instructions panic

Infinities seen…

Infinities seen… int BIG = 10000000; Michael E.

Infinities seen… int BIG = 10000000; grid[j][k] = 1000000; Michael E. Scott P.

Infinities seen… int BIG = 10000000; grid[j][k] = 1000000; paths[i][j] = 9001; Michael E. Scott P. Martin P.

Infinities seen… int BIG = 10000000; grid[j][k] = 1000000; paths[i][j] = 9001; direct = 2400; Michael E. Scott P. Martin P. Russ R.

Infinities seen… int BIG = 10000000; grid[j][k] = 1000000; paths[i][j] = 9001; direct = 2400; int constant = 1000; Michael E. Scott P. Martin P. Russ R. Zvi E.

Infinities seen… int BIG = 10000000; grid[j][k] = 1000000; paths[i][j] = 9001; direct = 2400; int constant = 1000; public static int Inf = 200; Michael E. Scott P. Martin P. Russ R. Zvi E. George T.

Infinities seen… int BIG = 10000000; Michael E. grid[j][k] = 1000000; Scott P. paths[i][j] = 9001; Martin P. direct = 2400; Russ R. int constant = 1000; Zvi E. public static int Inf = 200; George T. adjacency[a][b] = 0; Andrew H.

Infinities seen… int BIG = 10000000; Michael E. grid[j][k] = 1000000; Scott P. paths[i][j] = 9001; Martin P. direct = 2400; Russ R. int constant = 1000; Zvi E. public static int Inf = 200; George T. adjacency[a][b] = 100; Andrew H. int infinity = 31; Kwang K.

Infinities seen… int BIG = 10000000; Michael E. grid[j][k] = 1000000; Scott P. paths[i][j] = 9001; Martin P. direct = 2400; Russ R. int constant = 1000; Zvi E. public static int Inf = 200; George T. adjacency[a][b] = 100; Andrew H. int infinity = 31; Kwang K. #define INFINITE 0 x 0 fffffff Andrew F.

Infinities seen… int hashnode(char *buf) { int hv = 0; while(*buf) { hv <<= 6; hv |= *buf++ & 31; } return hv; } int BIG = 10000000; Michael E. grid[j][k] = 1000000; Scott P. paths[i][j] = 9001; Martin P. direct = 2400; Russ R. int constant = 1000; Zvi E. public static int Inf = 200; George T. adjacency[a][b] = 100; Andrew H. int infinity = 31; Kwang K. #define INFINITE 0 x 0 fffffff Andrew F. 268435455 for (int woo = 0; woo < tries; woo++) {

Schedule 10/2/2007 Today -- search and related problems 10/9/2007 Lab / mock contest 10/16/2007 10/23/2007 one more algorithm No class: conference & fall break… 10/30/2007 Real mock contest - "real" rules apply 9 pm to 1 am Tuesday, 10/30 11/6/2007 Meeting for ACM teams 11/13/2007 Final CS 189 meeting: contest wrap-up

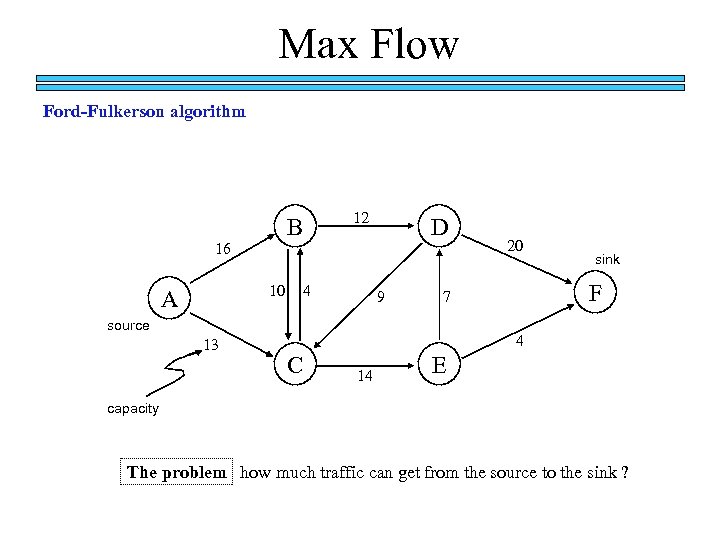Max Flow Ford-Fulkerson algorithm B 16 10 A 12 4 D 9 sink F 7 source 13 20 4 C 14 E capacity The problem how much traffic can get from the source to the sink ?

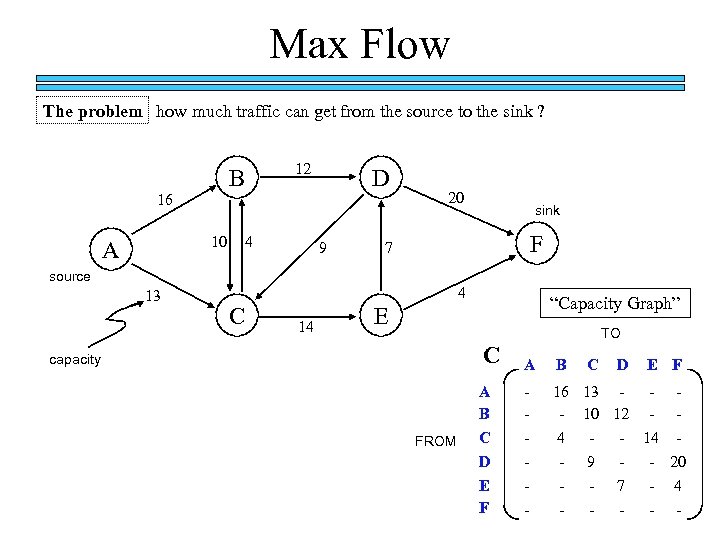
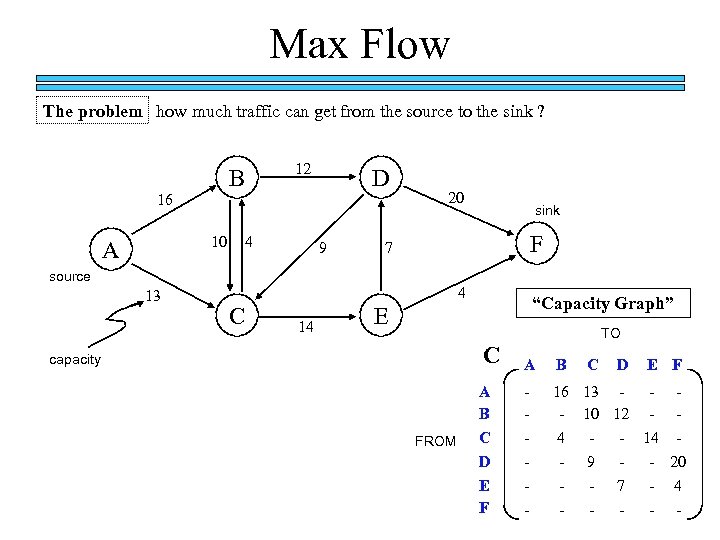Max Flow The problem how much traffic can get from the source to the sink ? B 16 10 A 12 4 D 9 20 F 7 source 13 sink 4 C 14 “Capacity Graph” E C capacity FROM A B C D E F TO A B - 16 13 - - 10 12 - 4 - 14 - 9 - 20 - - C - D 7 - E F - 4 -

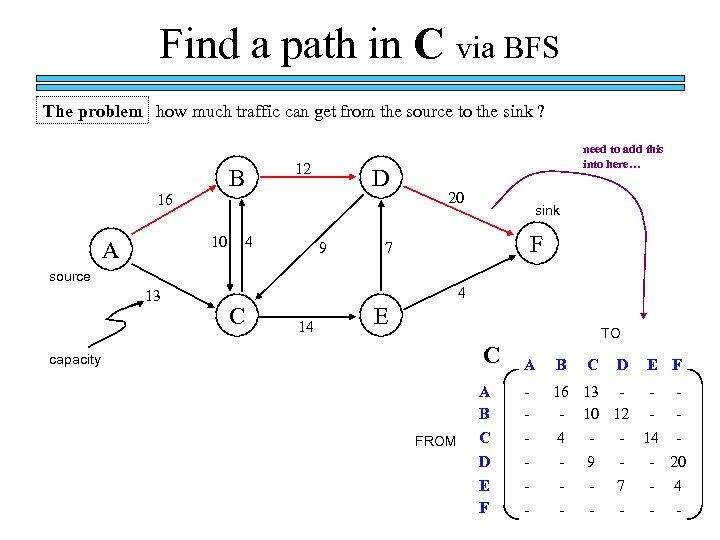Find a path in C via BFS The problem how much traffic can get from the source to the sink ? B 16 10 A 12 4 D 9 need to add this into here… 20 F 7 source 13 sink 4 C 14 E C capacity FROM A B C D E F TO A B - 16 13 - - 10 12 - 4 - 14 - 9 - 20 - - C - D 7 - E F - 4 -

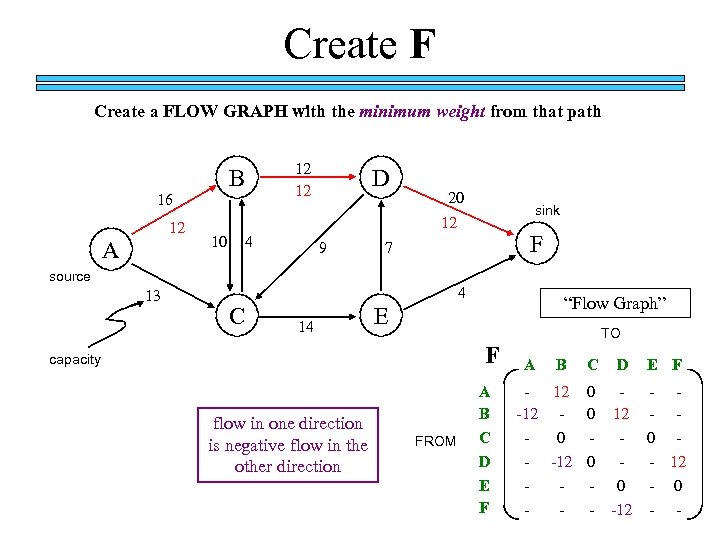
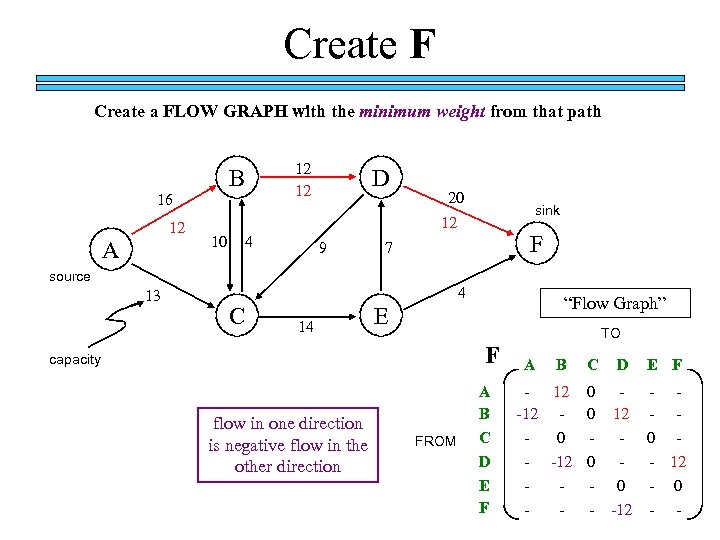Create F Create a FLOW GRAPH with the minimum weight from that path B 16 12 A 12 12 D 20 12 10 4 9 F 7 source 13 sink 4 C 14 “Flow Graph” E F capacity flow in one direction is negative flow in the other direction FROM A B C D E F TO A C D E F - 12 0 -12 - 0 0 - -12 0 12 - - - 0 - 12 0 -12 - - B - - 0 -

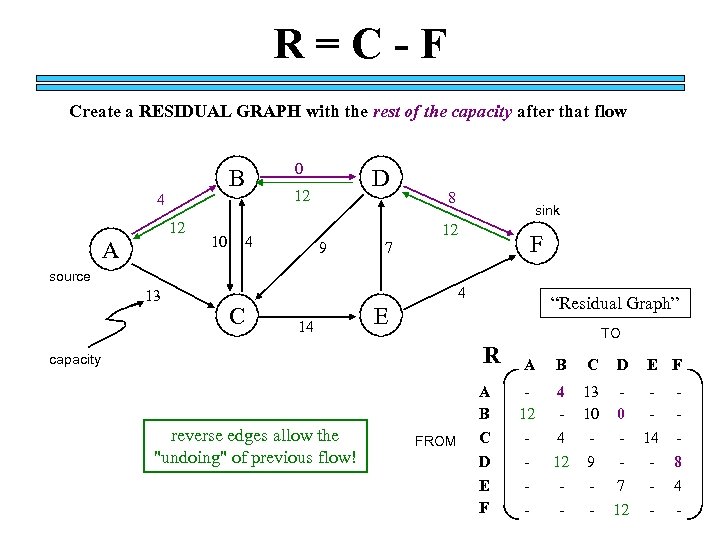
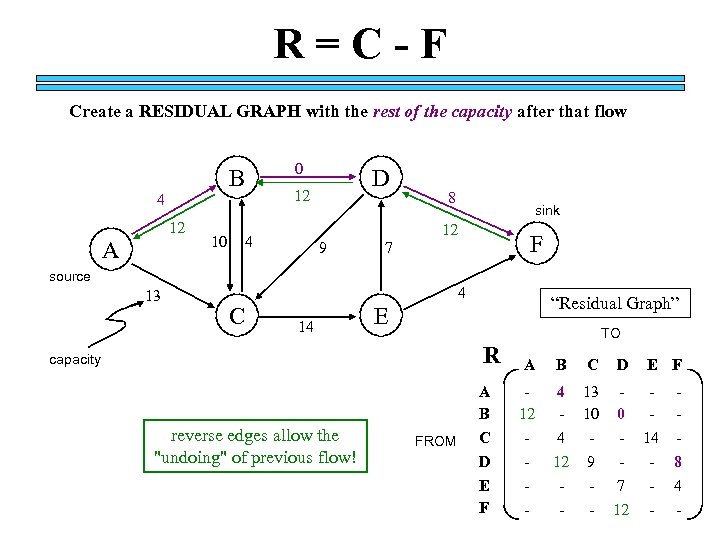R=C-F Create a RESIDUAL GRAPH with the rest of the capacity after that flow B 4 12 A 10 0 D 12 8 12 4 9 F 7 source 13 sink 4 C 14 “Residual Graph” E R capacity reverse edges allow the "undoing" of previous flow! FROM A B C D E F TO A 12 - B C D E F 4 13 - 10 4 12 9 0 - - - 14 - 8 - - 7 12 - 4 -

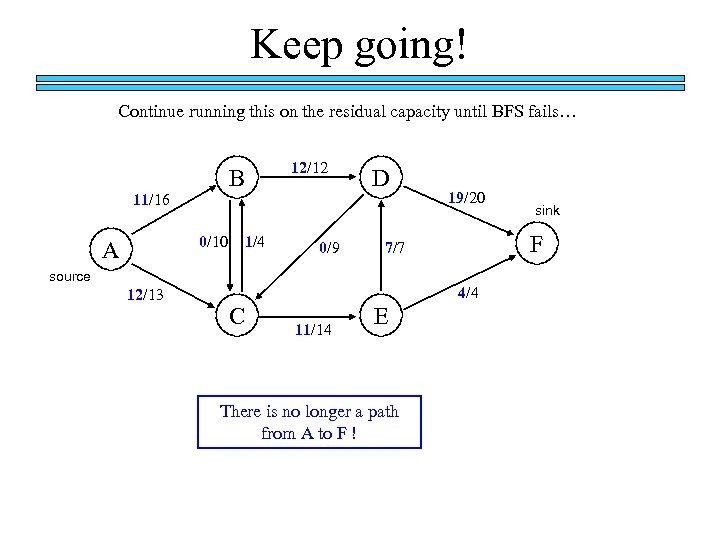Keep going! Continue running this on the residual capacity until BFS fails… B 11/16 0/10 A 1/4 12/12 0/9 D 4/4 C 11/14 E There is no longer a path from A to F ! sink F 7/7 source 12/13 19/20

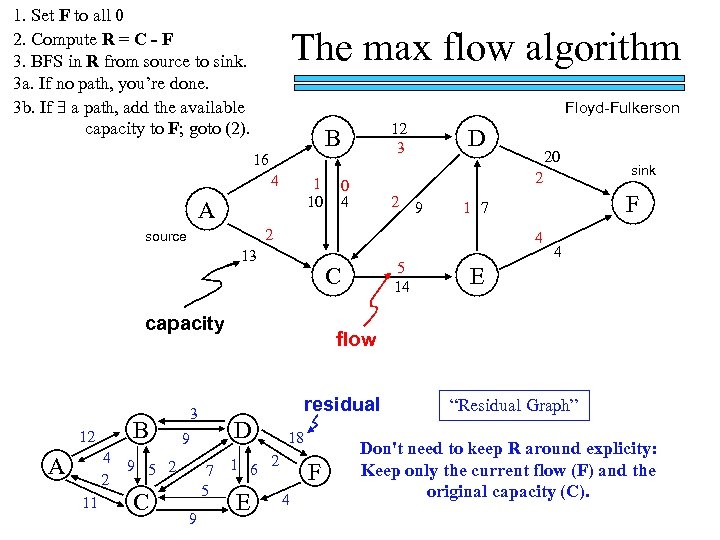1. Set F to all 0 2. Compute R = C - F 3. BFS in R from source to sink. 3 a. If no path, you’re done. 3 b. If a path, add the available capacity to F; goto (2). The max flow algorithm Floyd-Fulkerson 16 4 1 10 A 4 2 A 11 0 4 2 9 sink F 1 7 4 E flow D 7 5 9 5 14 residual 9 9 5 2 C capacity 3 20 4 13 B D 2 source 12 12 3 B 1 6 E 18 2 F 4 “Residual Graph” Don't need to keep R around explicity: Keep only the current flow (F) and the original capacity (C).

Pseudo-code (Python) def edmonds_karp(C, source, sink): n = len(C) # C is the capacity matrix F = [[0] * n for i in range(n)] # F is the flow matrix # residual capacity from u to v is C[u][v] - F[u][v] while True: path = BFS(C, F, source, sink) if not path: break flow = float(1 e 309) # Infinity ! # traverse path to find smallest capacity for (u, v) in path: flow = min(flow, C[u][v] - F[u][v]) # traverse path to update flow for u, v in path: F[u][v] += flow F[v][u] -= flow return sum([F[source][i] for i in xrange(n)]) Get into the flow! A little bit of name contention… edmonds_karp is really Ford-Fulkerson, but with other people getting the credit… def BFS(C, F, source, sink): queue = [source] paths = {source: []} while queue: u = queue. pop(0) for v in range(len(C)): if C[u][v] - F[u][v] > 0 and v not in paths: # Python == English ! paths[v] = paths[u] + [(u, v)] if v == sink: return paths[v] queue. append(v) return None

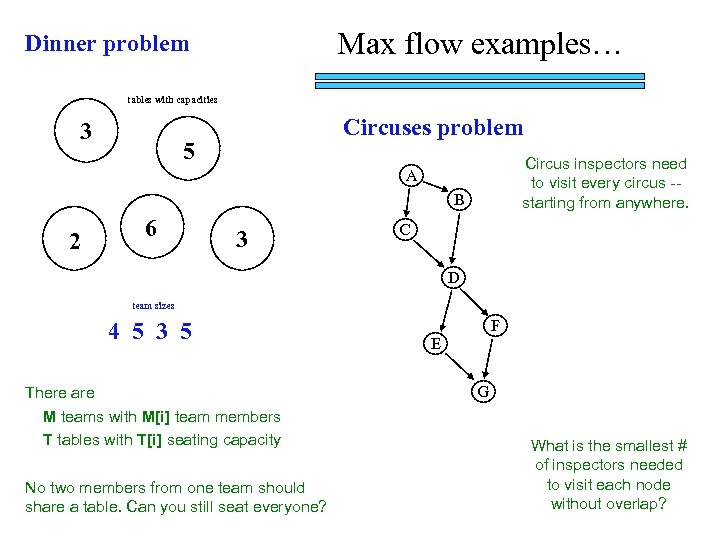Max flow examples… Dinner problem tables with capacities 3 Circuses problem 5 Circus inspectors need to visit every circus -starting from anywhere. A B 2 6 3 C D team sizes 4 5 3 5 There are M teams with M[i] team members T tables with T[i] seating capacity No two members from one team should share a table. Can you still seat everyone? F E G What is the smallest # of inspectors needed to visit each node without overlap?

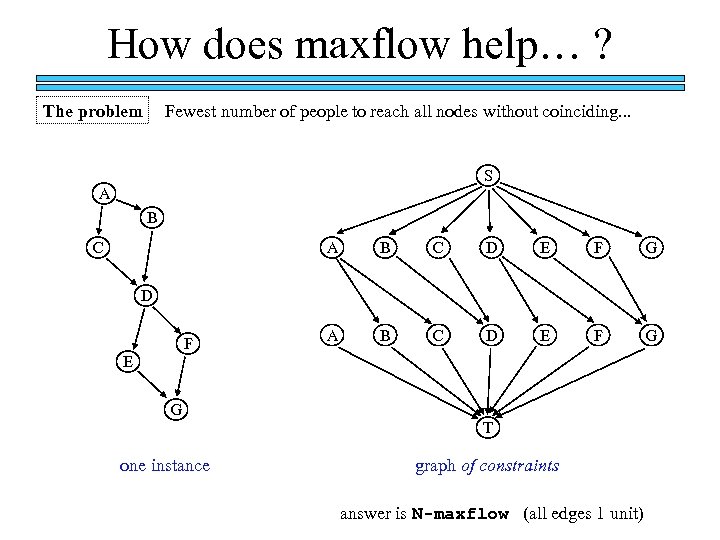How does maxflow help… ? The problem Fewest number of people to reach all nodes without coinciding. . . S A B C D E F G D F E G T one instance graph of constraints answer is N-maxflow (all edges 1 unit)

Pseudo-code (Python) def edmonds_karp(C, source, sink): n = len(C) # C is the capacity matrix F = [[0] * n for i in range(n)] # F is the flow matrix # residual capacity from u to v is C[u][v] - F[u][v] while True: path = BFS(C, F, source, sink) if not path: break flow = float(1 e 309) # Infinity ! # traverse path to find smallest capacity for (u, v) in path: flow = min(flow, C[u][v] - F[u][v]) # traverse path to update flow for u, v in path: F[u][v] += flow F[v][u] -= flow return sum([F[source][i] for i in xrange(n)]) def BFS(C, F, source, sink): queue = [source] paths = {source: []} while queue: u = queue. pop(0) for v in range(len(C)): if C[u][v] - F[u][v] > 0 and v not in paths: paths[v] = paths[u] + [(u, v)] if v == sink: return paths[v] queue. append(v) return None Get into the flow! A little bit of name contention… edmonds_karp is really Floyd-Fulkerson, but with other people getting the credit… many problems require no more than BFS or DFS

Problem Set #5: Search algorithms, etc. orchard gumbo getout sq circuses

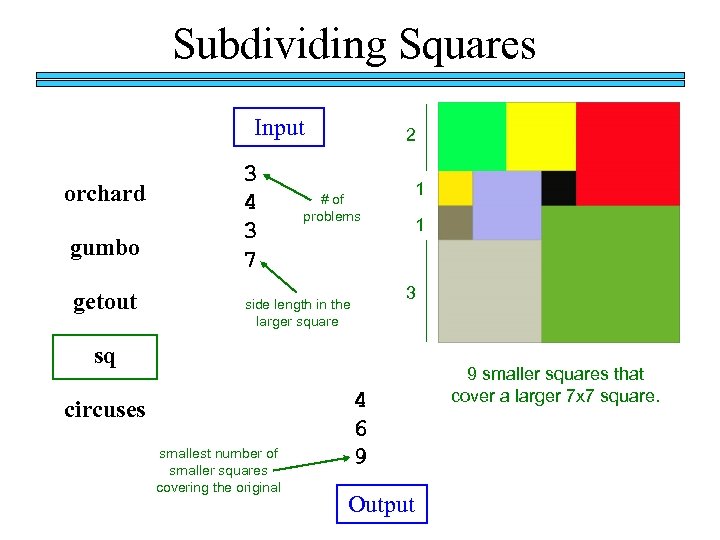Subdividing Squares Input orchard gumbo getout 3 4 3 7 2 1 # of problems 1 3 side length in the larger square sq circuses smallest number of smaller squares covering the original 4 6 9 Output 9 smaller squares that cover a larger 7 x 7 square.

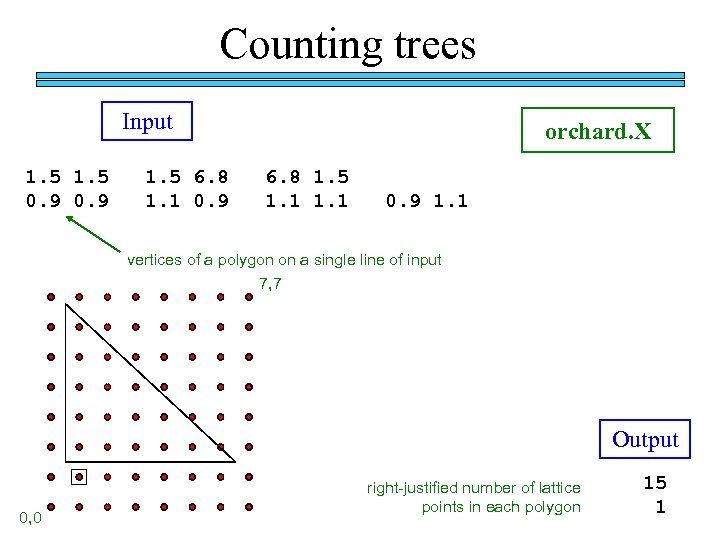Counting trees Input 1. 5 0. 9 1. 5 6. 8 1. 1 0. 9 orchard. X 6. 8 1. 5 1. 1 0. 9 1. 1 vertices of a polygon on a single line of input 7, 7 Output 0, 0 right-justified number of lattice points in each polygon 15 1

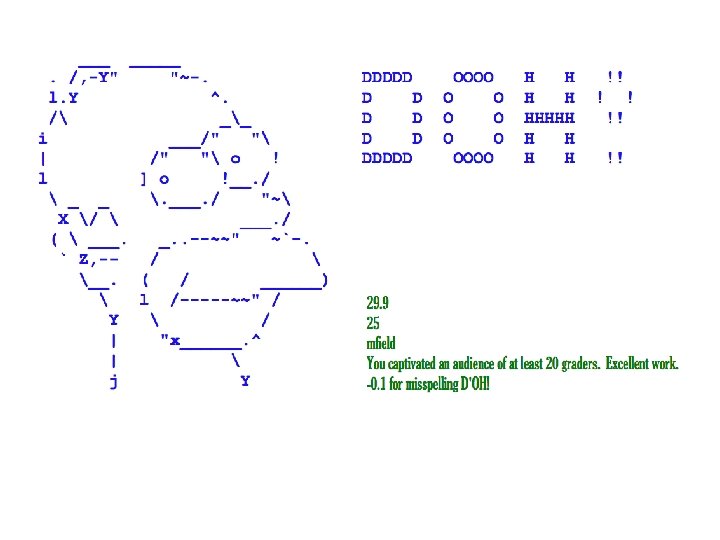
Java Geometry

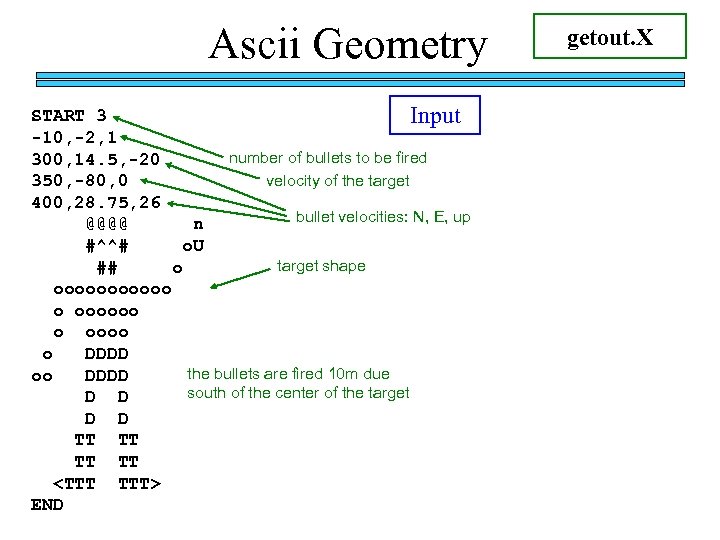Ascii Geometry START 3 Input -10, -2, 1 number of bullets to be fired 300, 14. 5, -20 velocity of the target 350, -80, 0 400, 28. 75, 26 bullet velocities: N, E, up @@@@ n #^^# o. U target shape ## o oooooo o DDDD the bullets are fired 10 m due oo DDDD south of the center of the target D D TT TT END getout. X

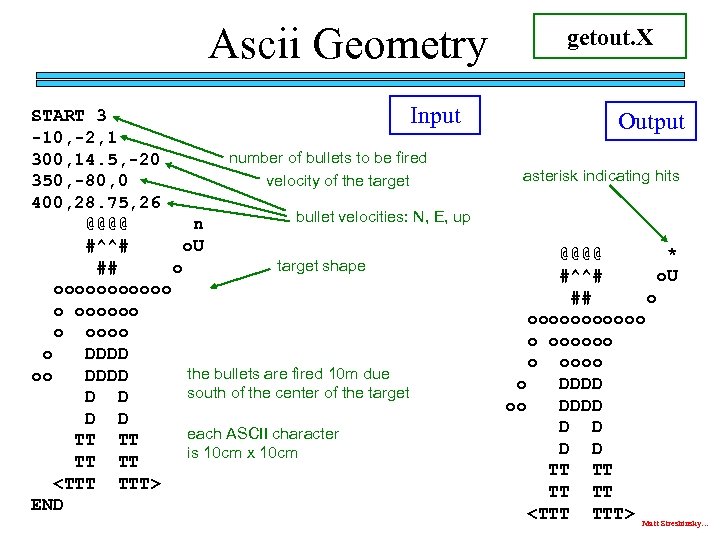Ascii Geometry START 3 Input -10, -2, 1 number of bullets to be fired 300, 14. 5, -20 velocity of the target 350, -80, 0 400, 28. 75, 26 bullet velocities: N, E, up @@@@ n #^^# o. U target shape ## o oooooo o DDDD the bullets are fired 10 m due oo DDDD south of the center of the target D D each ASCII character TT TT is 10 cm x 10 cm TT TT END getout. X Output asterisk indicating hits @@@@ * #^^# o. U ## o oooooo o DDDD oo DDDD D D TT TT Matt Streshinsky…

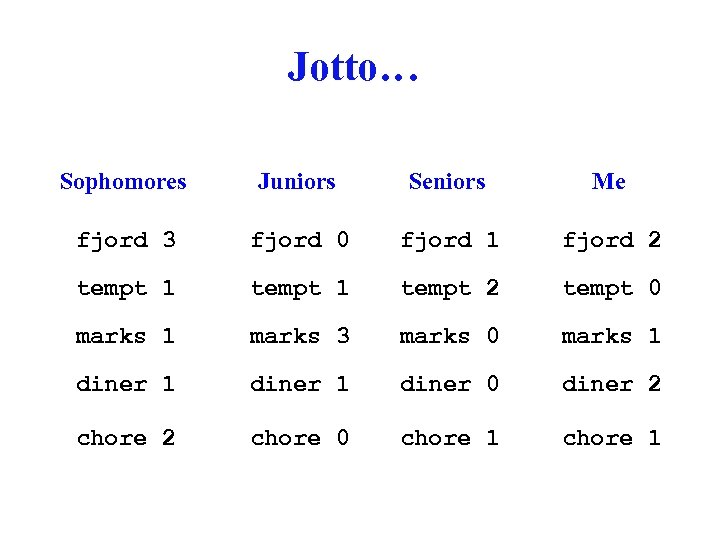Jotto… Sophomores Juniors Seniors Me fjord 3 fjord 0 fjord 1 fjord 2 tempt 1 tempt 2 tempt 0 marks 1 marks 3 marks 0 marks 1 diner 0 diner 2 chore 0 chore 1

See you next week!

ACM today The Fall competition is getting organized…

Schedule 10/2/2007 Today -- search and misc problems 10/9/2007 Lab / mock contest 10/16/2007 10/23/2007 No class: conference & fall break… 10/30/2007 Real mock contest - "real" rules apply 9 pm to 1 am Tuesday, 10/30 11/6/2007 Meeting for ACM teams 11/13/2007 Final CS 189 meeting: contest wrap-up

Max Flow The problem how much traffic can get from the source to the sink ? B 16 10 A 12 4 D 9 20 F 7 source 13 sink 4 C 14 “Capacity Graph” E C capacity FROM A B C D E F TO A B - 16 13 - - 10 12 - 4 - 14 - 9 - 20 - - C - D 7 - E F - 4 -

Create F Create a FLOW GRAPH with the minimum weight from that path B 16 12 A 12 12 D 20 12 10 4 9 F 7 source 13 sink 4 C 14 “Flow Graph” E F capacity flow in one direction is negative flow in the other direction FROM A B C D E F TO A C D E F - 12 0 -12 - 0 0 - -12 0 12 - - - 0 - 12 0 -12 - - B - - 0 -

R=C-F Create a RESIDUAL GRAPH with the rest of the capacity after that flow B 4 12 A 10 0 D 12 8 12 4 9 F 7 source 13 sink 4 C 14 “Residual Graph” E R capacity reverse edges allow the "undoing" of previous flow! FROM A B C D E F TO A 12 - B C D E F 4 13 - 10 4 12 9 0 - - - 14 - 8 - - 7 12 - 4 -

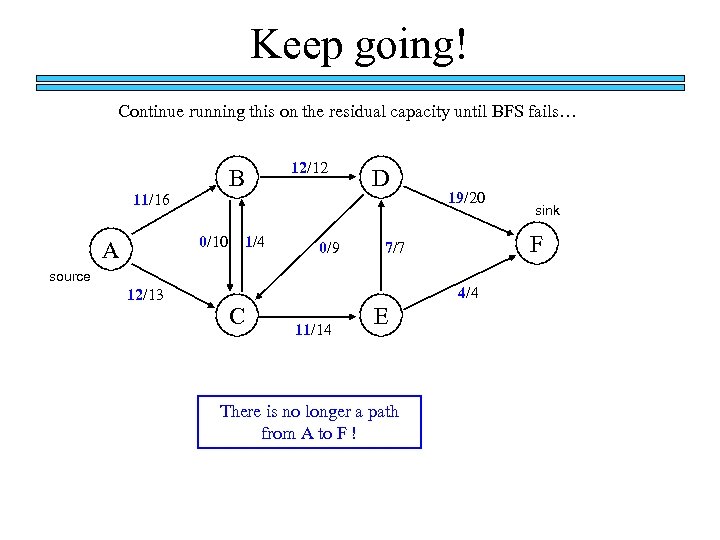Keep going! Continue running this on the residual capacity until BFS fails… B 11/16 0/10 A 1/4 12/12 0/9 D 4/4 C 11/14 E There is no longer a path from A to F ! sink F 7/7 source 12/13 19/20

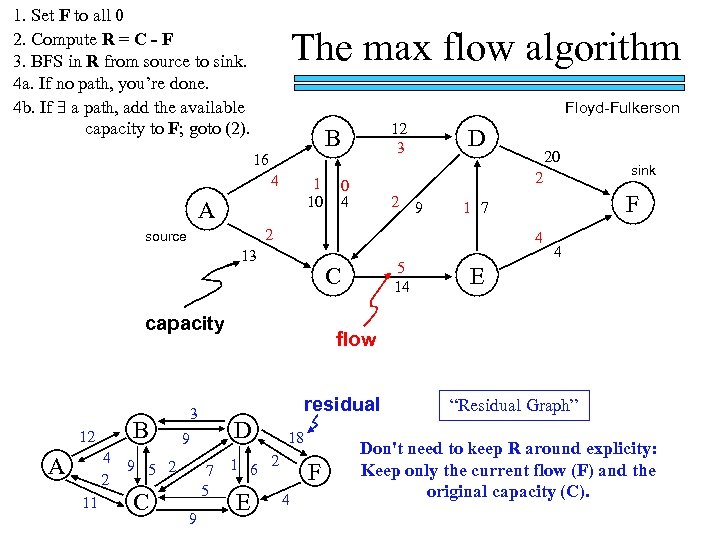1. Set F to all 0 2. Compute R = C - F 3. BFS in R from source to sink. 4 a. If no path, you’re done. 4 b. If a path, add the available capacity to F; goto (2). The max flow algorithm Floyd-Fulkerson 16 4 1 10 A 4 2 A 11 0 4 2 9 sink F 1 7 4 E flow D 7 5 9 5 14 residual 9 9 5 2 C capacity 3 20 4 13 B D 2 source 12 12 3 B 1 6 E 18 2 F 4 “Residual Graph” Don't need to keep R around explicity: Keep only the current flow (F) and the original capacity (C).

Pseudo-code (Python) def edmonds_karp(C, source, sink): n = len(C) # C is the capacity matrix F = [[0] * n for i in range(n)] # F is the flow matrix # residual capacity from u to v is C[u][v] - F[u][v] while True: path = BFS(C, F, source, sink) if not path: break flow = float(1 e 309) # Infinity ! # traverse path to find smallest capacity for (u, v) in path: flow = min(flow, C[u][v] - F[u][v]) # traverse path to update flow for u, v in path: F[u][v] += flow F[v][u] -= flow return sum([F[source][i] for i in xrange(n)]) def BFS(C, F, source, sink): queue = [source] paths = {source: []} while queue: u = queue. pop(0) for v in range(len(C)): if C[u][v] - F[u][v] > 0 and v not in paths: paths[v] = paths[u] + [(u, v)] if v == sink: return paths[v] queue. append(v) return None Get into the flow! A little bit of name contention… edmonds_karp is really Floyd-Fulkerson, but with other people getting the credit…

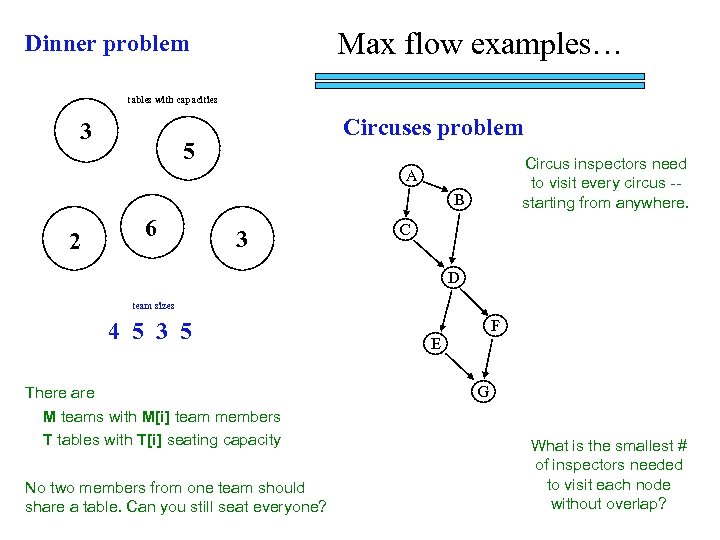Max flow examples… Dinner problem tables with capacities 3 Circuses problem 5 Circus inspectors need to visit every circus -starting from anywhere. A B 2 6 3 C D team sizes 4 5 3 5 There are M teams with M[i] team members T tables with T[i] seating capacity No two members from one team should share a table. Can you still seat everyone? F E G What is the smallest # of inspectors needed to visit each node without overlap?

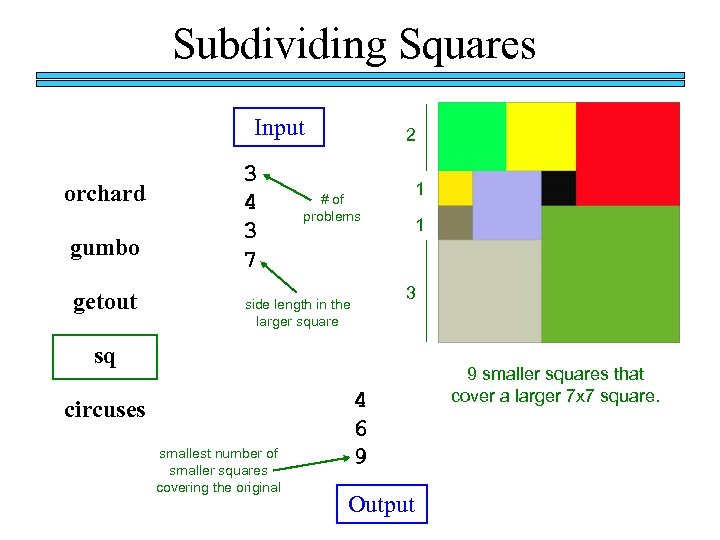Subdividing Squares Input orchard gumbo getout 3 4 3 7 2 1 # of problems 1 3 side length in the larger square sq circuses smallest number of smaller squares covering the original 4 6 9 Output 9 smaller squares that cover a larger 7 x 7 square.

Java Geometry

Jotto… Sophomores Juniors Seniors Me fjord 3 fjord 0 fjord 1 fjord 2 tempt 1 tempt 2 tempt 0 marks 1 marks 3 marks 0 marks 1

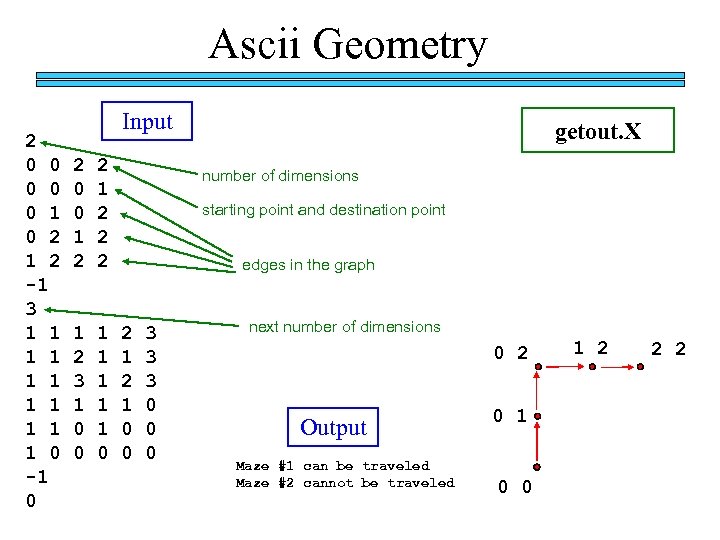Ascii Geometry 2 0 0 0 1 0 2 1 2 -1 3 1 1 1 0 -1 0 Input 2 0 0 1 2 2 2 1 2 3 1 0 0 1 1 1 0 getout. X number of dimensions starting point and destination point edges in the graph 2 1 0 0 3 3 3 0 0 0 next number of dimensions 0 2 Output Maze #1 can be traveled Maze #2 cannot be traveled 0 1 0 0 1 2 2 2