Abstraction and Modular Reasoning for the Verification of

Abstraction and Modular Reasoning for the Verification of Software Corina Pasareanu NASA Ames Research Center

Outline l Bandera Project (Kansas Sate University): – Tool Support for Program Abstraction and Abstract Counter-example Analysis (joint work with the Bandera team) l NASA Ames Projects: – Combining Symbolic Execution with (Explicit State) Model Checking (joint work with Willem Visser) – Assumption Generation for Component Verification (joint work with Dimitra Giannakopoulou and Howard Barringer)

Outline l Bandera Project (Kansas Sate University): – Tool Support for Program Abstraction and Abstract Counter-example Analysis l NASA Ames Projects: – Combining Symbolic Execution with (Explicit State) Model Checking – Assumption Generation for Component Verification

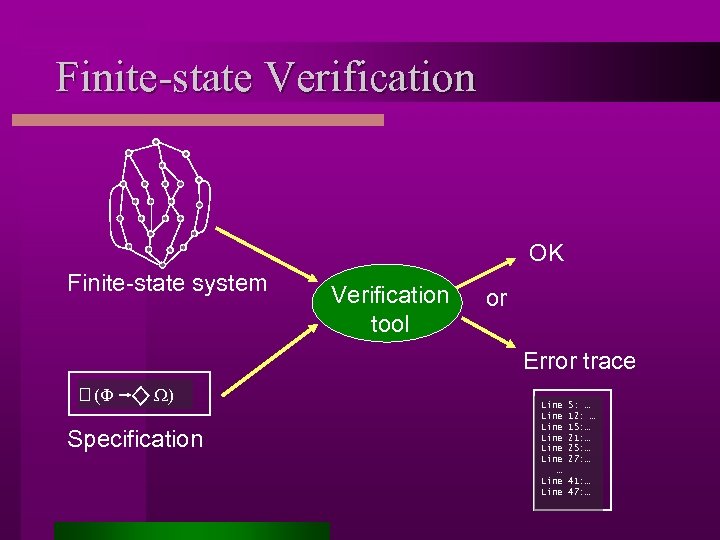
Finite-state Verification OK Finite-state system Verification tool or Error trace (F W) Specification Line Line … Line 5: … 12: … 15: … 21: … 25: … 27: … 41: … 47: …

Finite-State Verification l Effective for analyzing properties of hardware systems Widespread success and adoption in industry l Recent years have seen many efforts to apply those techniques to software Limited success due to the enormous state spaces associated with most software systems

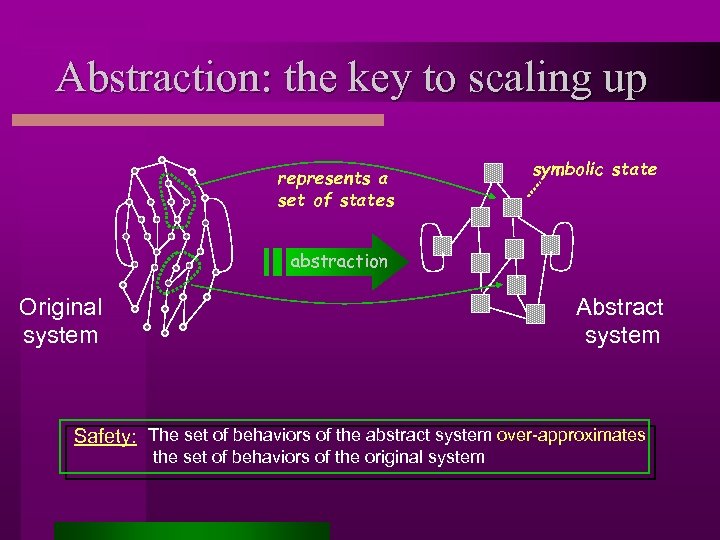
Abstraction: the key to scaling up represents a set of states symbolic state abstraction Original system Abstract system Safety: The set of behaviors of the abstract system over-approximates the set of behaviors of the original system

Goals of our work … Develop multiple forms of tool support for abstraction that is… … applicable to program source code … largely automated … usable by non-experts Evaluate the effectiveness of this tool support through… … implementation in the Bandera toolset … application to real multi-threaded Java programs

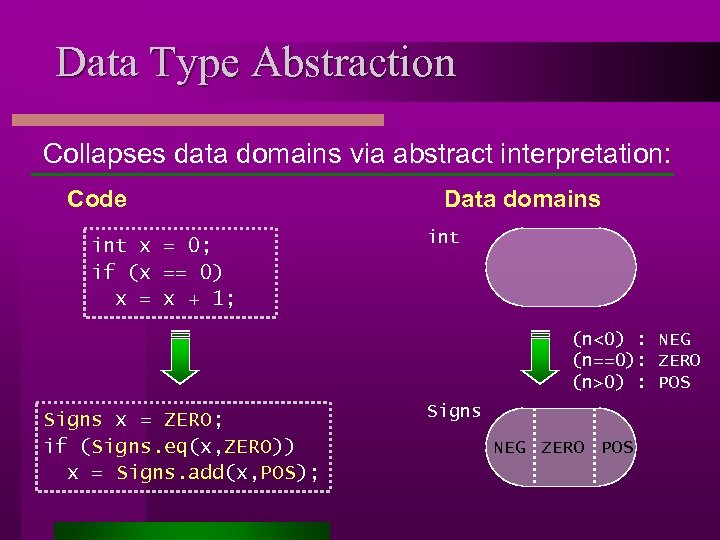
Data Type Abstraction Collapses data domains via abstract interpretation: Code int x = 0; if (x == 0) x = x + 1; Data domains int (n<0) : NEG (n==0): ZERO (n>0) : POS Signs x = ZERO; if (Signs. eq(x, ZERO)) x = Signs. add(x, POS); Signs NEG ZERO POS

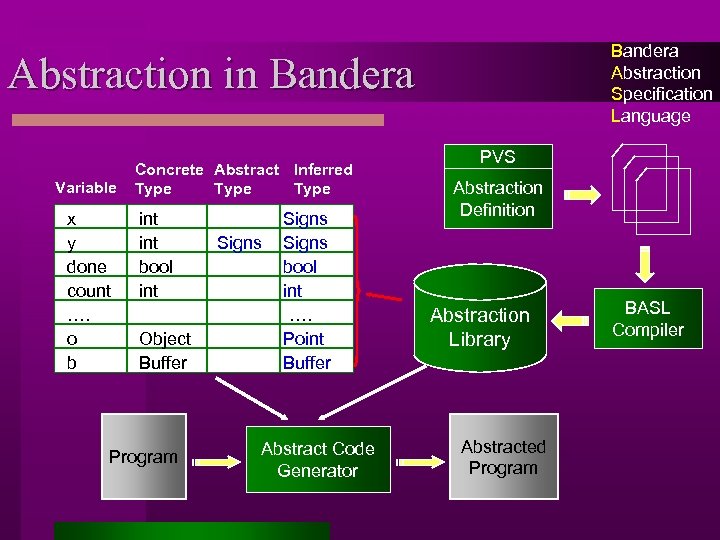
Bandera Abstraction Specification Language Abstraction in Bandera Variable x y done count …. o b Concrete Abstract Inferred Type int bool int Object Buffer Program Signs bool int …. Point Buffer Abstract Code Generator PVS Abstraction Definition Abstraction Library Abstracted Program BASL Compiler

Definition of Abstractions in BASL abstraction Signs abstracts int begin TOKENS = { NEG, ZERO, POS }; abstract(n) begin n < 0 n == 0 n > 0 end -> {NEG}; -> {ZERO}; -> {POS}; Automatic Generation operator + add begin (NEG , NEG) -> {NEG} ; (NEG , ZERO) -> {NEG} ; (ZERO, NEG) -> {NEG} ; (ZERO, ZERO) -> {ZERO} ; (ZERO, POS) -> {POS} ; (POS , ZERO) -> {POS} ; (POS , POS) -> {POS} ; (_, _) -> {NEG, ZERO, POS}; /* case (POS, NEG), (NEG, POS) */ end Example: Start safe, then refine: +(NEG, NEG)={NEG, ZERO, POS} Proof obligations submitted to PVS. . . Forall n 1, n 2: neg? (n 1) and neg? (n 2) implies not pos? (n 1+n 2) Forall n 1, n 2: neg? (n 1) and neg? (n 2) implies not zero? (n 1+n 2) Forall n 1, n 2: neg? (n 1) and neg? (n 2) implies not neg? (n 1+n 2)

Compiling BASL Definitions abstraction Signs abstracts int begin TOKENS = { NEG, ZERO, POS }; abstract(n) begin n < 0 n == 0 n > 0 end -> {NEG}; -> {ZERO}; -> {POS}; public class Signs { public static final int NEG = 0; // mask 1 public static final int ZERO = 1; // mask 2 public static final int POS = 2; // mask 4 public static int abs(int n) { if (n < 0) return NEG; if (n == 0) return ZERO; if (n > 0) return POS; } operator + add public static int add(int arg 1, int arg 2) { begin Compiled if (arg 1==NEG && arg 2==NEG) return NEG; (NEG , NEG) -> {NEG} ; if (arg 1==NEG && arg 2==ZERO) return NEG; (NEG , ZERO) -> {NEG} ; if (arg 1==ZERO && arg 2==NEG) return NEG; (ZERO, NEG) -> {NEG} ; if (arg 1==ZERO && arg 2==ZERO) return ZERO; (ZERO, ZERO) -> {ZERO} ; if (arg 1==ZERO && arg 2==POS) return POS; (ZERO, POS) -> {POS} ; if (arg 1==POS && arg 2==ZERO) return POS; (POS , ZERO) -> {POS} ; if (arg 1==POS && arg 2==POS) return POS; (POS , POS) -> {POS} ; return Bandera. choose(7); (_, _)-> {NEG, ZERO, POS}; /* case (POS, NEG), (NEG, POS) */ } end

Abstract Counter-example Analysis l For an abstracted program, a counter-example may be infeasible because: – Over-approximation introduced by abstraction l Example: x = -2; if(x + 2 == 0) then. . . x = NEG; if(Signs. eq(Signs. add(x, POS), ZERO)) then. . . {NEG, ZERO, POS}

Our Solutions l Choice-bounded State Space Search – “on-the-fly”, during model checking l Abstract Counter-example Guided Concrete Simulation – Exploit implementations of abstractions for Java programs – Effective in practice – Implemented in Java Path. Finder tool

“Choose”-free state space search l Theorem [Saidi: SAS’ 00] Every path in the abstracted program where all assignments are deterministic is a path in the concrete program. l Bias the model checker – to look only at paths that do not include instructions that introduce non-determinism l JPF model checker modified – to detect non-deterministic choice (i. e. calls to Bandera. choose()); backtrack from those points

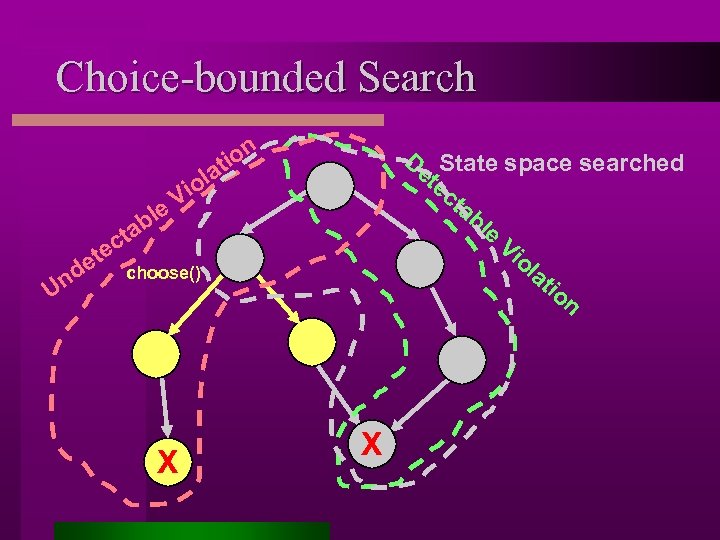
Choice-bounded Search De State space searched te ct ab le Vi ol at io n a l io e. V l on ti b ta c te de choose() Un X X

Case Study: DEOS Kernel (NASA Ames) l Honeywell Dynamic Enforcement Operating System (DEOS) – – l A real time operating system for integrated modular avionics Non-trivial concurrent program (1433 lines of code, 20 classes, 6 threads) Written in C++, translated into Java and Promela With a known bug Verification of the system exhausted 4 Gigabytes of memory without completion; abstraction needed Abstracted using data type abstraction l Checked using JPF and SPIN l Defect detected using choice-bounded search l

Conclusion and Future Research Directions Tool support for abstraction enables verification of real properties of real programs l Extend abstraction support for objects l – Heap abstractions to handle an unbounded number of dynamically allocated objects – Handle recursive procedures, unbounded number of processes l Extend automation – For selection and refinement based on counterexample analysis

Outline l Bandera Project (Kansas Sate University): – Tool Support for Program Abstraction and Abstract Counter-example Analysis l NASA Ames Projects: – Combining Symbolic Execution with (Explicit State) Model Checking – Assumption Generation for Component Verification

Java Path Finder (NASA Ames) Model checker for Java programs l Built on top of a custom made Java Virtual Machine l Checks for deadlock and violation of assertions; LTL properties l Support for abstraction: l – Predicate abstraction – Bandera’s data abstraction l Heuristic search

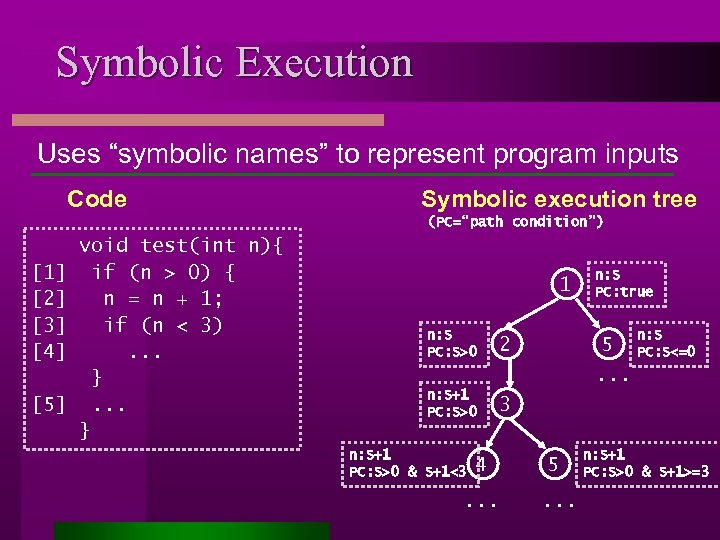
Symbolic Execution Uses “symbolic names” to represent program inputs Code Symbolic execution tree (PC=“path condition”) [1] [2] [3] [4] [5] void test(int n){ if (n > 0) { n = n + 1; if (n < 3). . . } 1 n: S PC: S>0 2 n: S+1 PC: S>0 n: S PC: true 3 n: S+1 PC: S>0 & S+1<3 n: S 5 PC: S<=0. . . 4 5 . . . n: S+1 PC: S>0 & S+1>=3

Symbolic Execution and JPF: Applications l Extends JPF with a new form of abstraction l Test case generation l Abstract counter-example analysis and refinement l Symbolic execution of multithreaded programs l Parameter synthesis …

Implementation in JPF l Easy: – Uses Bandera’s type abstraction – Uses Omega library (Java version) • Manipulates sets of linear constraints over integer variables Can be used as a “symbolic execution tool with backtracking” l Good for finding counter-examples l No state matching! l

(Possible) Implementation Code void test(int n) { if (n > 0) { n = n + 1; . . . } public class Sym. Val { public Sym. Val() {. . . } public Sym. Val(int n) {. . . } public Sym. Val(Sym. Val s 1, Sym. Val s 2, String ops) {. . . } public class Sym. Ops { public Sym. Val add(Sym. Val s 1, Sym. Val s 2){ return new Sym. Val(s 1, s 2, ’+’); } Path. Condition PC; // =“true” void test(Sym. Val n) { n = new Sym. Val(); if(Sym. Ops. gt(n, new Sym. Val(0)){ n=Sym. Ops. add(n, new Sym. Val(1)); . . . } public bool gt(Sym. Val s 1, Sym. Val s 2) { bool result = Verify. choose. Bool(); if(result) { // “true” PC. add. Condition(s 1, s 2, ’>’); } else { // “false” PC. add. Condition(s 1, s 2, ’<=‘); } PC. simplify(); return result; }. . . }

Problem: Convergence Symbolic execution tree Code [1] [2] [3] [4] void test(int n) { int x = 0; while(x < n) x = x + 1; } 1 2 n: S, x: 0 PC: 0<S n: S, x: 0 PC: true 3 n: S, x: 1 PC: 0<S n: S PC: true 2 n: S, x: 1 PC: 0<S & 1<S 3 . . 4 4 n: S, x: 0 PC: 0>=S n: S, x: 1 PC: 0<S & 1>=S

Problem: Convergence Solutions? l l l Limit the search depth of MC Unwind loops a fixed number of times (similar to Bounded MC? ) Discover “simple and practical” widening techniques Acceleration techniques Heuristics? Combine with “predicate abstraction” …

Relation to Bounded MC l Extend BMC with symbolic variables? l Widening for C programs? l…

Outline l Bandera Project (Kansas Sate University): – Tool Support for Program Abstraction and Abstract Counter-example Analysis l NASA Ames Projects: – Combining Symbolic Execution with (Explicit State) Model Checking – Assumption Generation for Component Verification

Assumption Generation for Component Verification l Problem: Component Environment Property ? Environment Assumption ? The “weakest” assumption A for component C: for all environments E, E |= A E || C |= P

Applications l Support for modular verification – Compositional verification – Property decomposition l Run-time monitoring of the environment l Component retrieval l Sub-module construction …

Implementation l In Labeled Transition Systems Analyzer (LTSA) tool - Imperial college – Supports compositional reachability analysis based on software architecture – Incremental system design and verification: • Component abstraction (hiding of internal actions) • Minimization wrt. observational equivalence – Both components and properties expressed as labeled transition systems

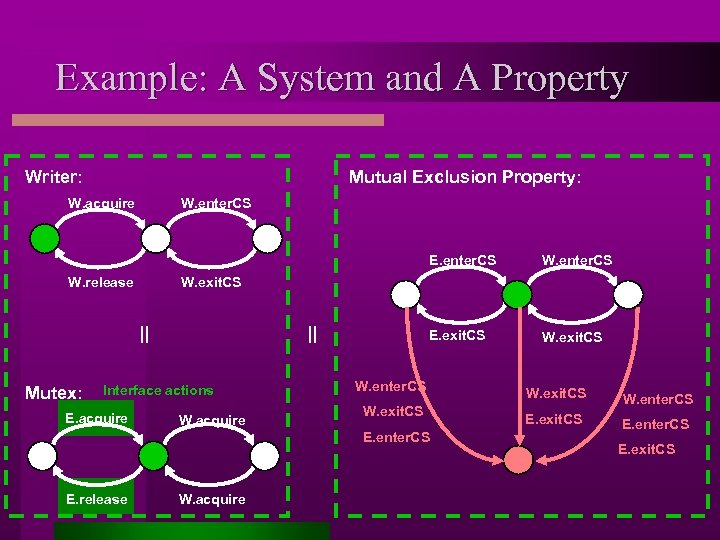
Example: A System and A Property Mutual Exclusion Property: Writer: W. acquire W. enter. CS E. enter. CS || || Interface actions E. acquire E. exit. CS W. release Mutex: W. enter. CS W. acquire W. enter. CS W. exit. CS E. enter. CS E. release W. acquire W. exit. CS W. enter. CS E. exit. CS E. enter. CS E. exit. CS

Assumption Generation Step 1: composition, hiding of internal actions and minimization Property true! (all environments) Step 2: backward reachability with error state Property false! (all environments) Step 3: property extraction (sub-set construction and completion) Assumption

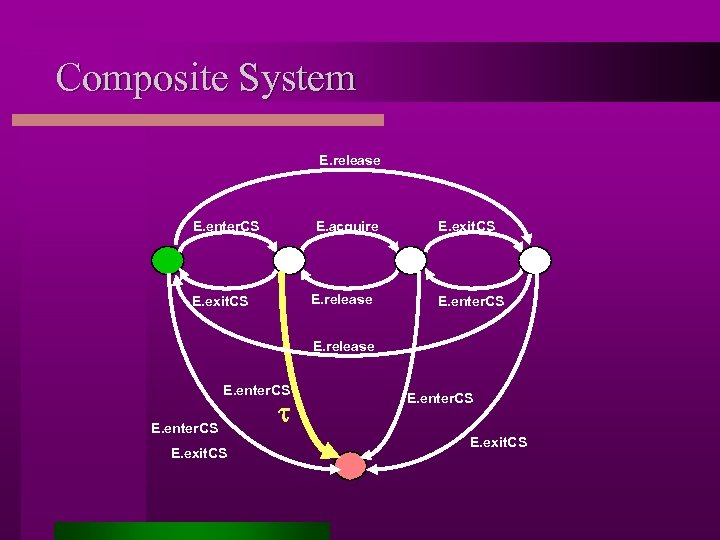
Composite System E. release E. enter. CS E. acquire E. release E. exit. CS E. enter. CS E. release E. enter. CS E. exit. CS t E. enter. CS E. exit. CS

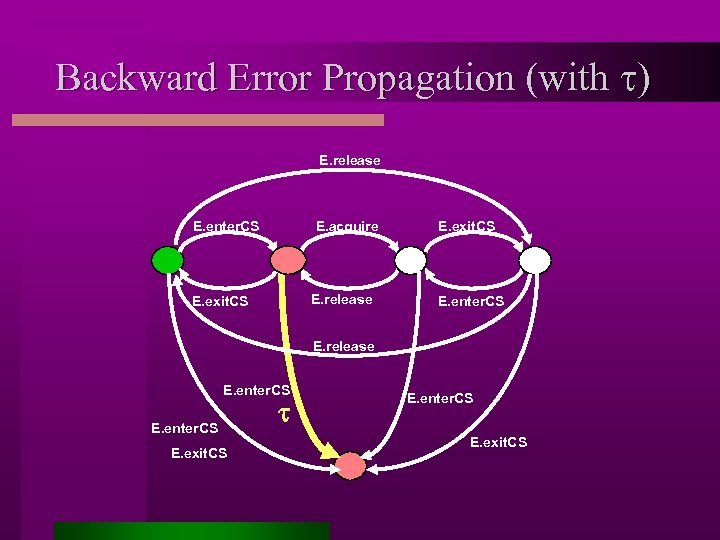
Backward Error Propagation (with t) E. release E. enter. CS E. acquire E. release E. exit. CS E. enter. CS E. release E. enter. CS E. exit. CS t E. enter. CS E. exit. CS

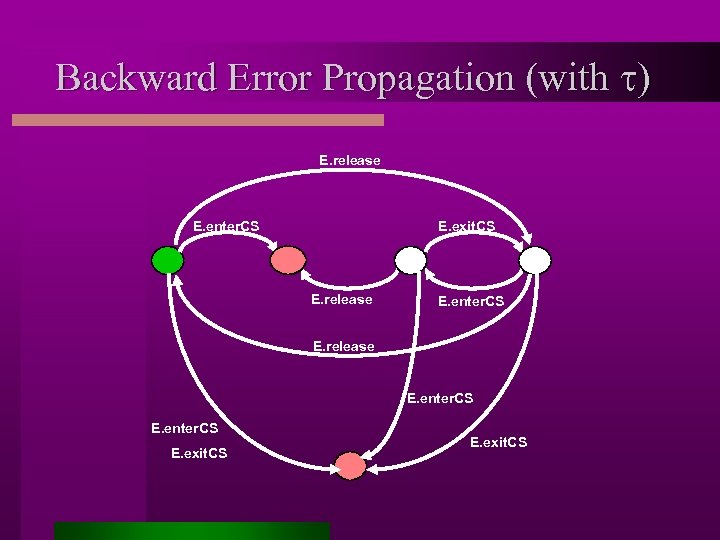
Backward Error Propagation (with t) E. release E. enter. CS E. exit. CS

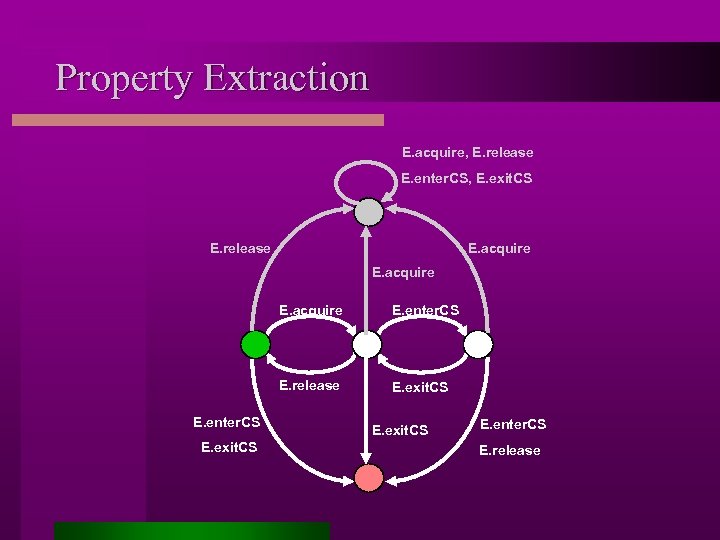
Property Extraction E. acquire, E. release E. enter. CS, E. exit. CS E. release E. acquire E. release E. enter. CS E. exit. CS E. enter. CS E. release

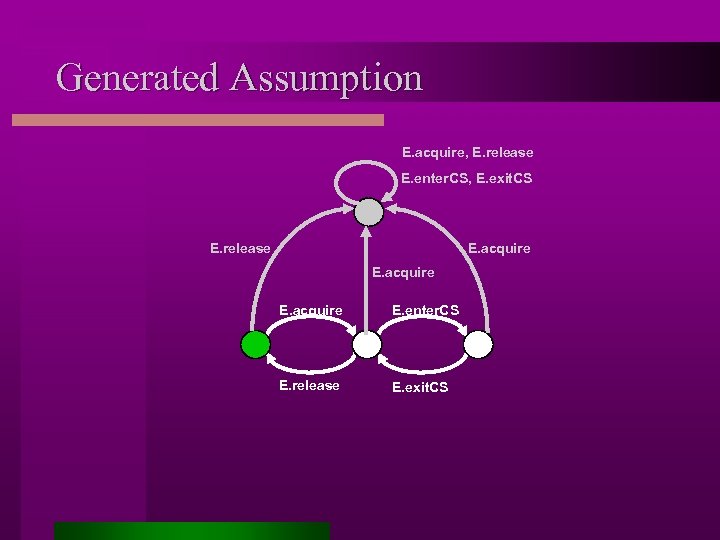
Generated Assumption E. acquire, E. release E. enter. CS, E. exit. CS E. release E. acquire E. enter. CS E. release E. exit. CS

Directions for Future Work l Liveness /fairness l Extend to other frameworks – LTL checking (since we are interested only in error behaviors) l Is the sub-set construction needed? l Study other forms of composition …