Abstract Data Types (ADTs)
Array-based Stack
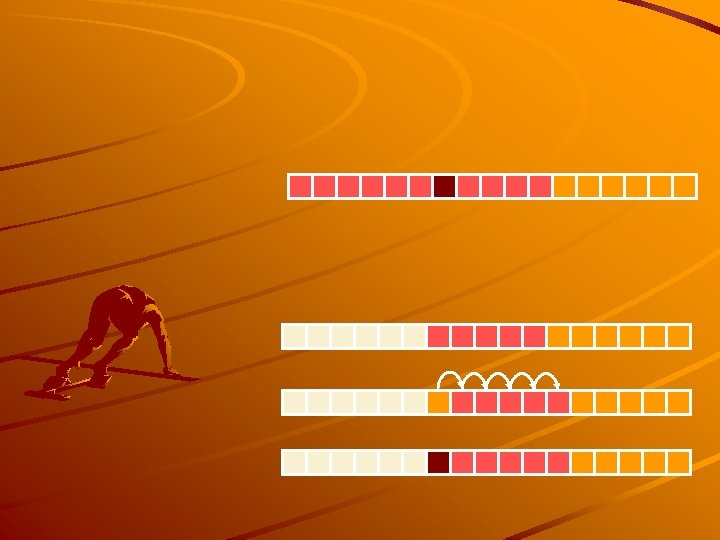
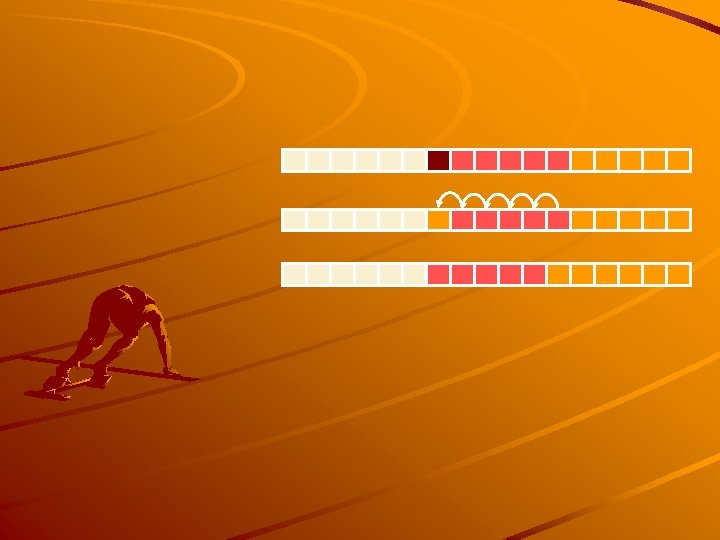
normal configuration wrapped-around configuration
We use the modulo operator (remainder of division) Operation enqueue throws an exception if the array is full This exception is implementation-dependent Operation dequeue throws an exception if the queue is empty This exception is specified in the queue ADT
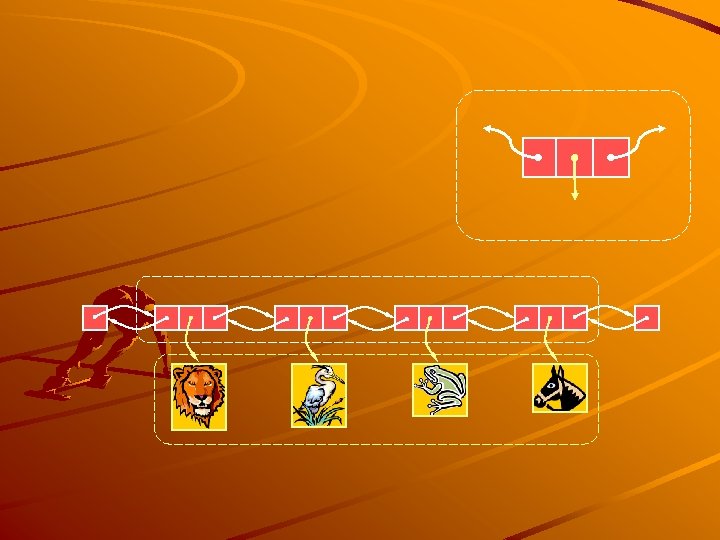
p A A p p B q B p A C B A C A B B C C X q X D p D C A B C
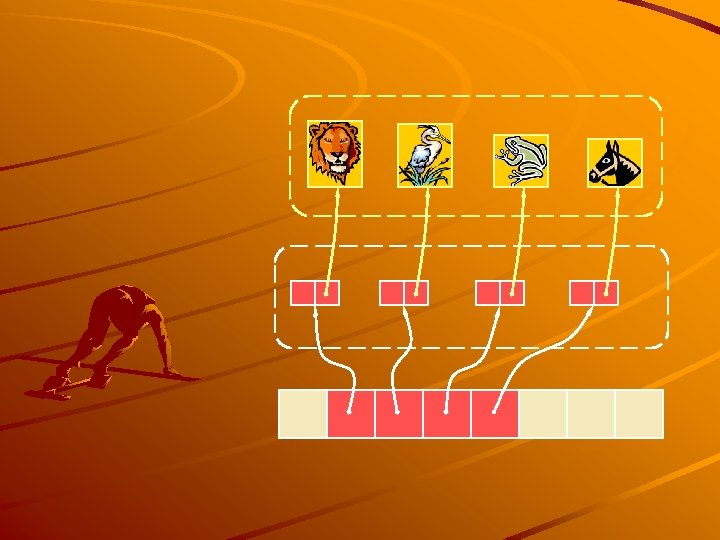
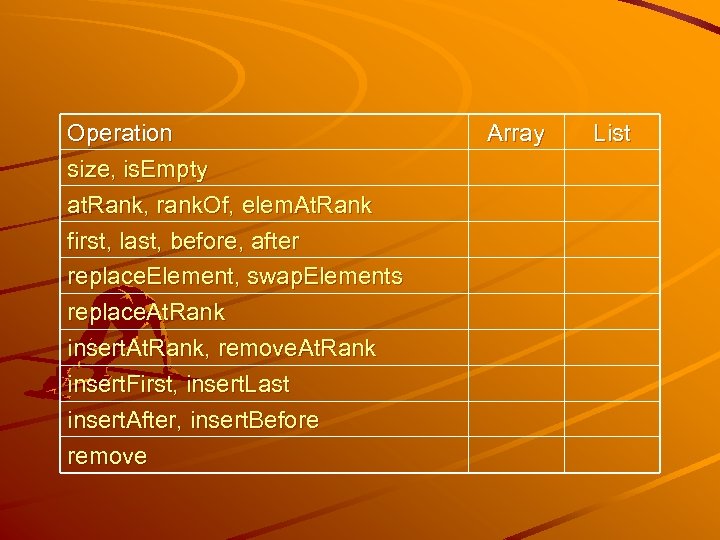
Operation size, is. Empty at. Rank, rank. Of, elem. At. Rank first, last, before, after replace. Element, swap. Elements replace. At. Rank insert. At. Rank, remove. At. Rank insert. First, insert. Last insert. After, insert. Before remove Array List
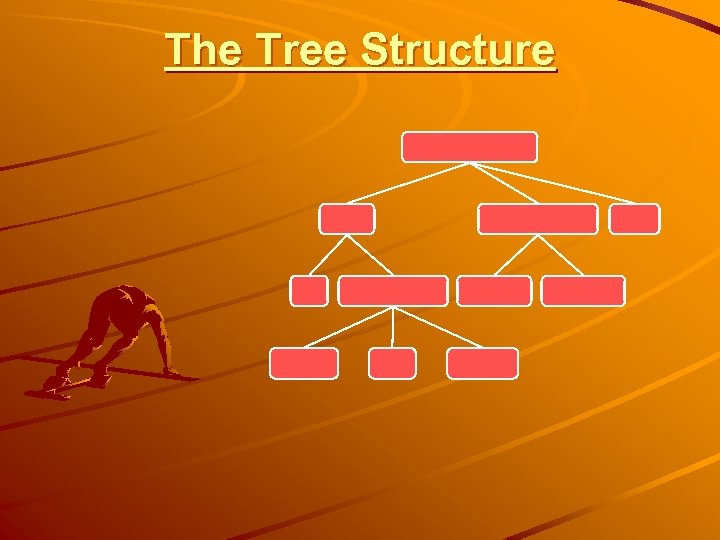
The Tree Structure
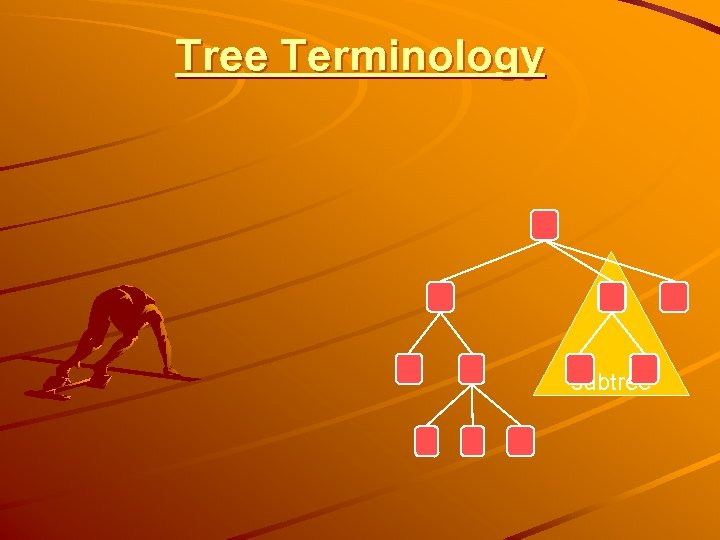
Tree Terminology subtree
Tree ADT
The Tree Structure
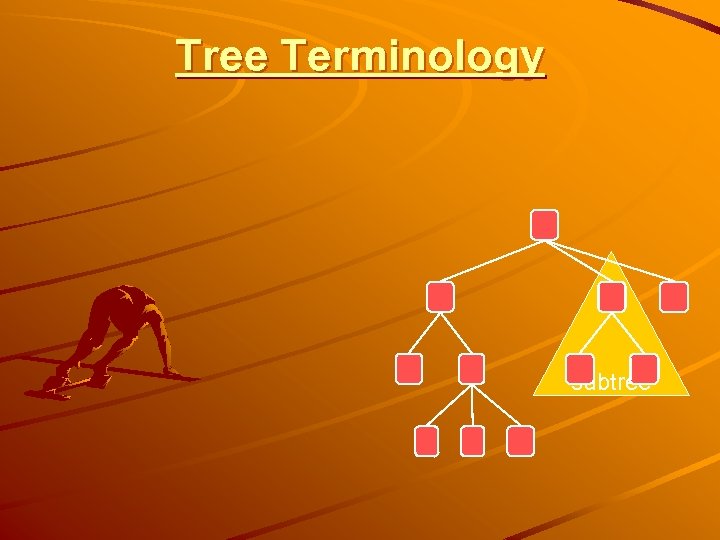
Tree Terminology subtree
Tree ADT
Depth and Height
Preorder Traversal
Postorder Traversal
Binary Tree
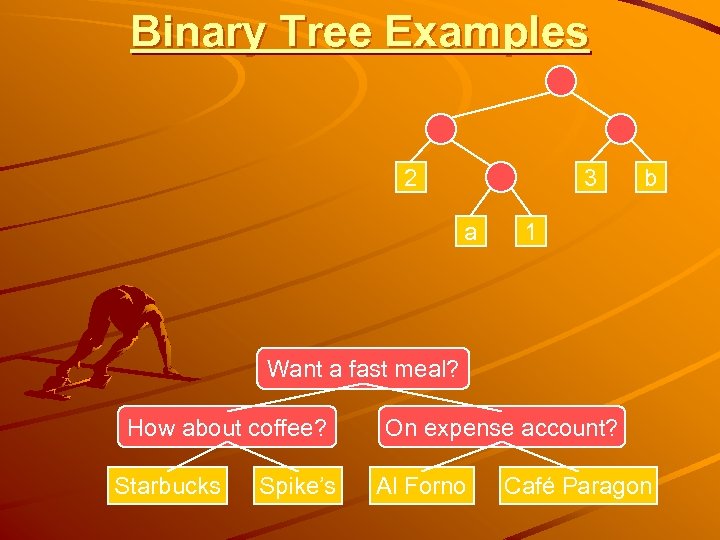
Binary Tree Examples 2 3 a b 1 Want a fast meal? How about coffee? Starbucks Spike’s On expense account? Al Forno Café Paragon
Properties of Binary Trees
Binary. Tree ADT
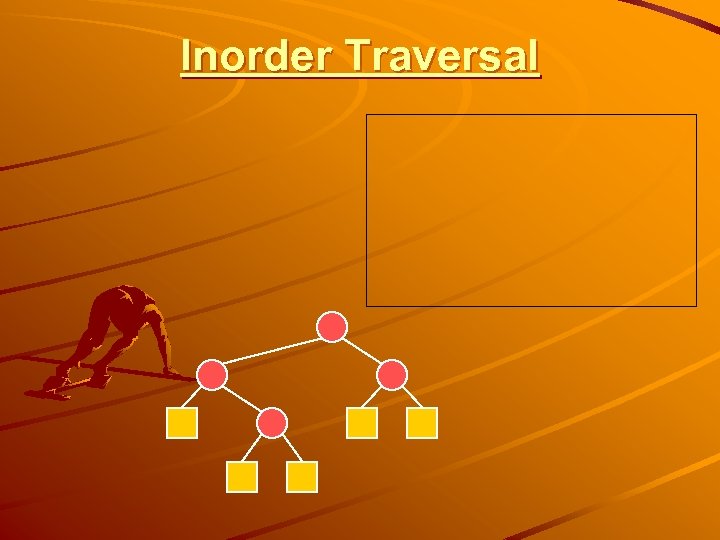
Inorder Traversal
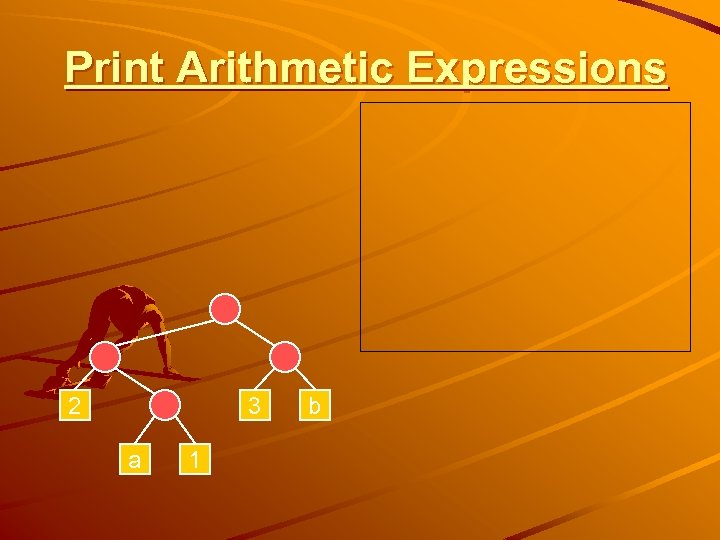
Print Arithmetic Expressions 2 3 a 1 b
2 3 5 1 2
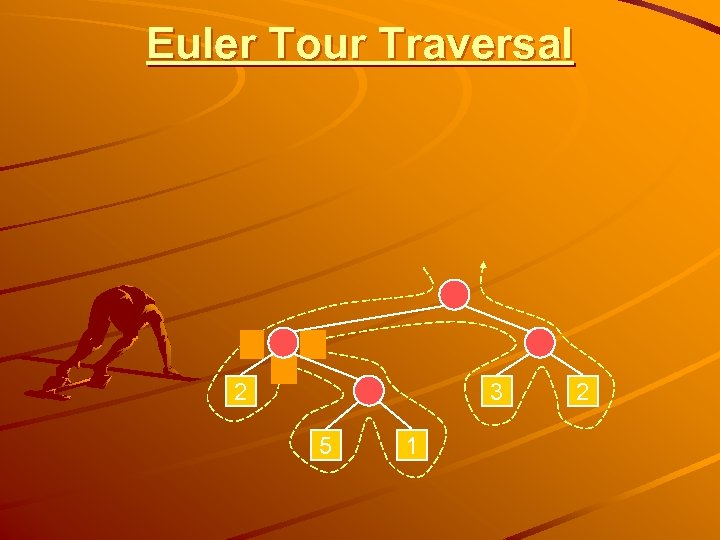
Euler Tour Traversal 2 3 5 1 2
Template Method Pattern
Specializations of Euler. Tour
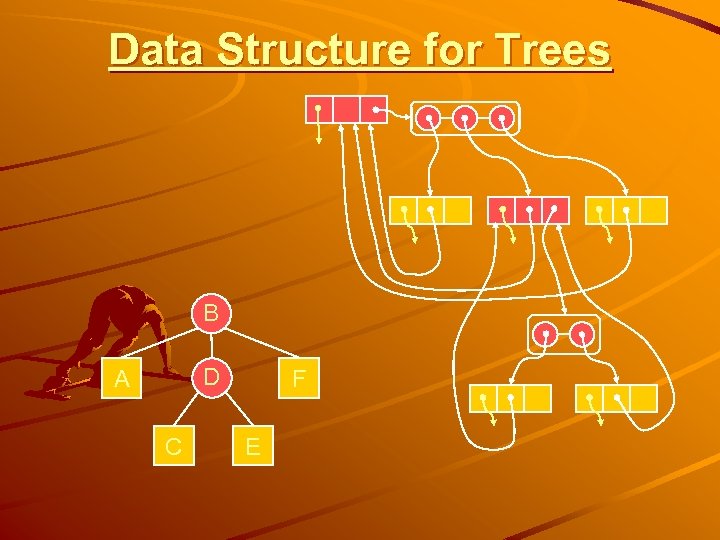
Data Structure for Trees B D A C F E
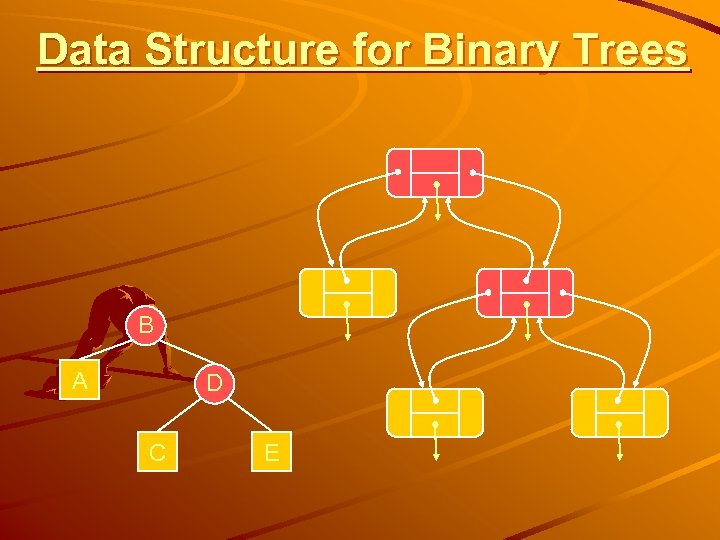
Data Structure for Binary Trees B A D C E
Java Implementation
Trees in JDSL
Priority Queue ADT
Total Order Relation
Comparator ADT
Sorting with a Priority Queue
Selection-Sort
Insertion-Sort
In-place Insertion-sort
What is a heap
Height of a Heap
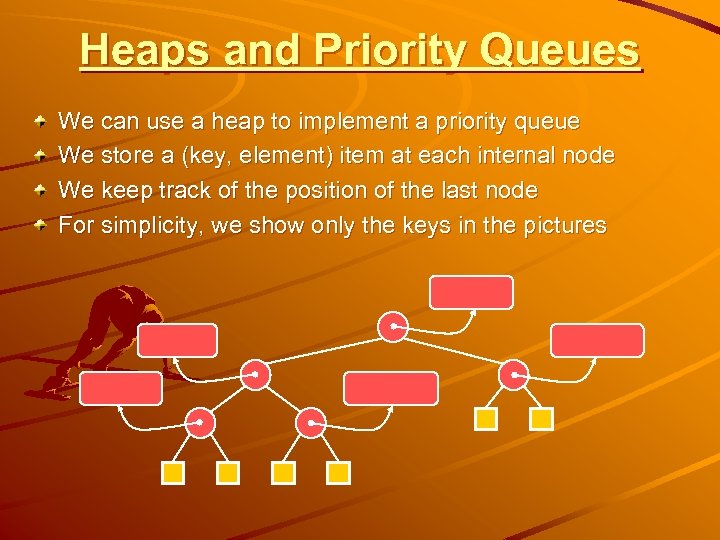
Heaps and Priority Queues We can use a heap to implement a priority queue We store a (key, element) item at each internal node We keep track of the position of the last node For simplicity, we show only the keys in the pictures
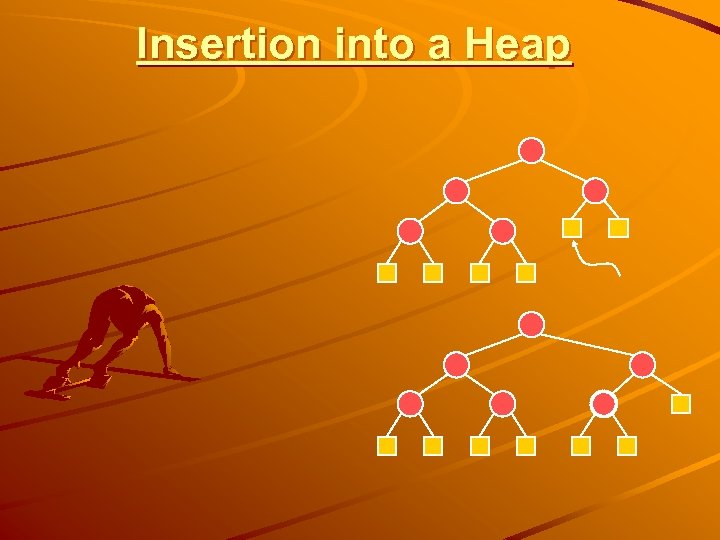
Insertion into a Heap
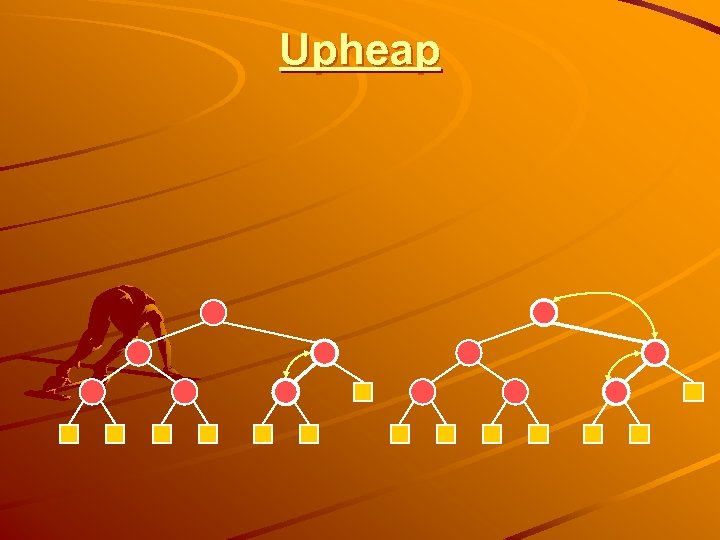
Upheap
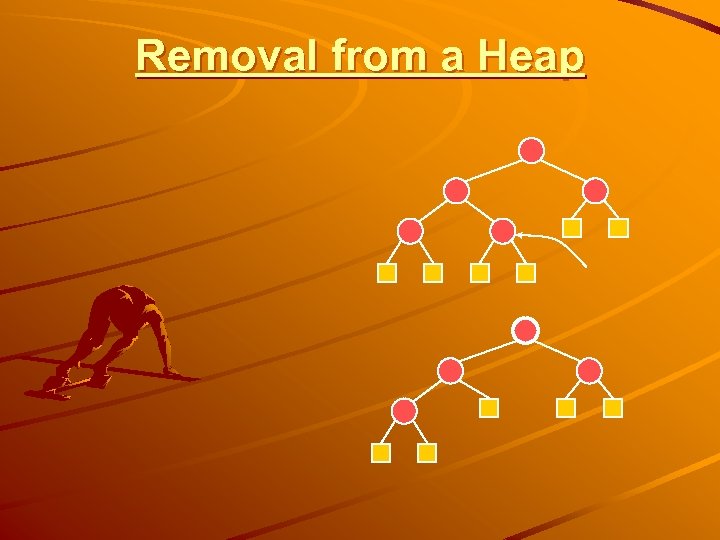
Removal from a Heap
Downheap
Updating the Last Node
Heap-Sort
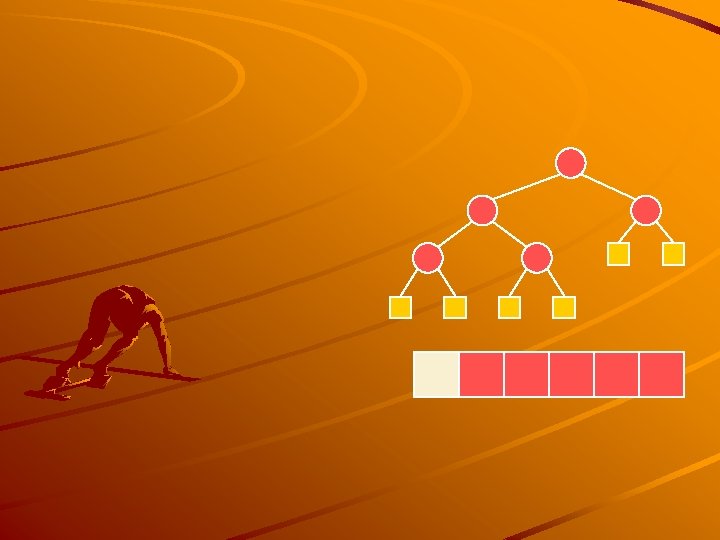
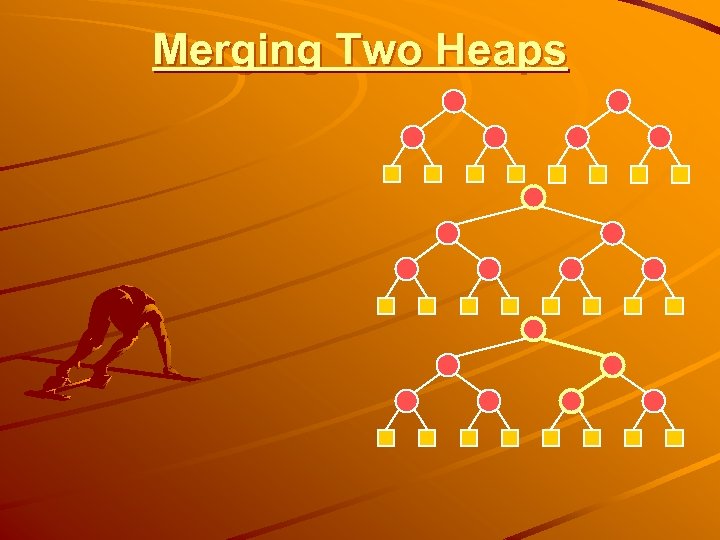
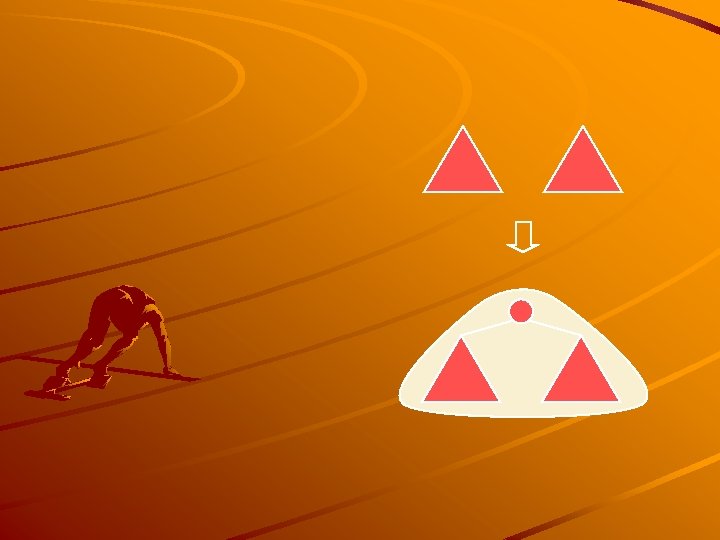
Merging Two Heaps
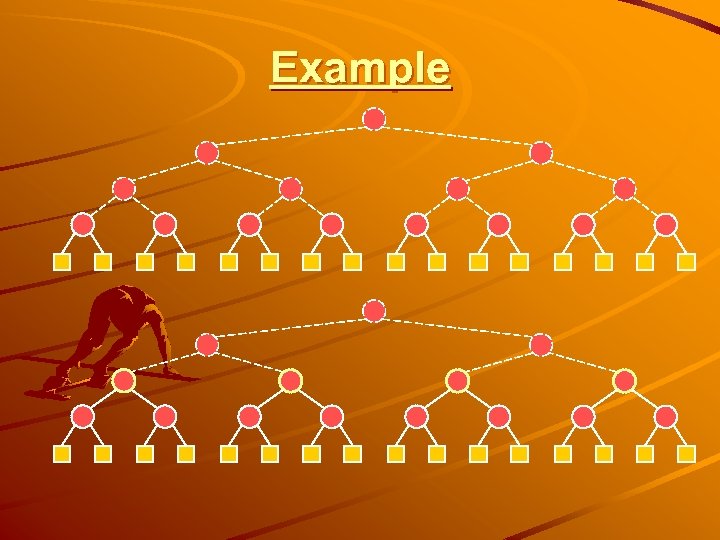
Example
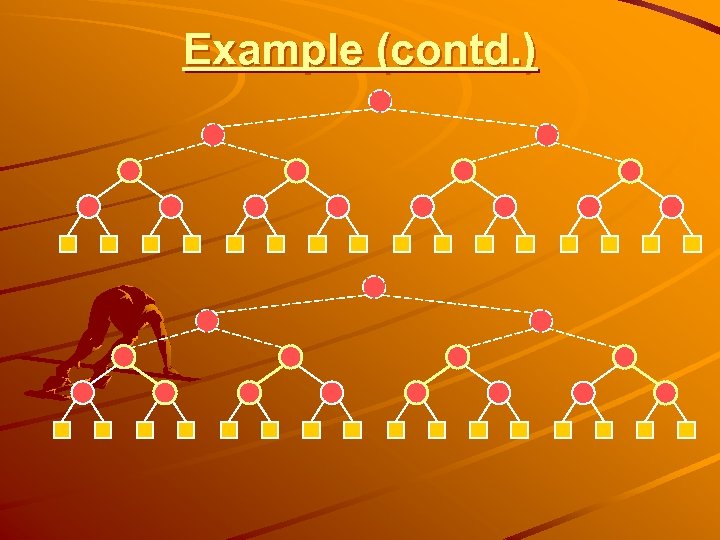
Example (contd. )
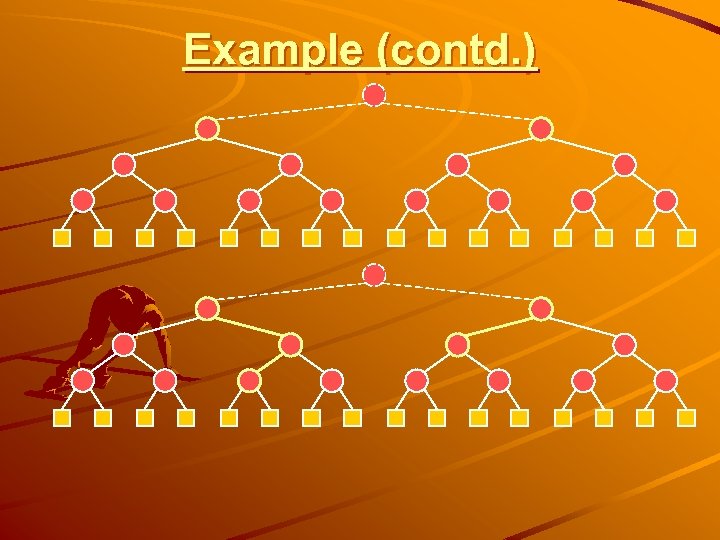
Example (contd. )
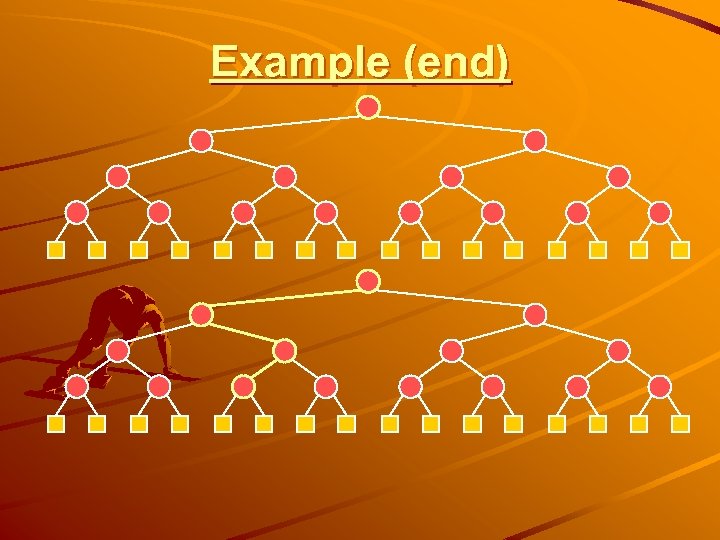
Example (end)
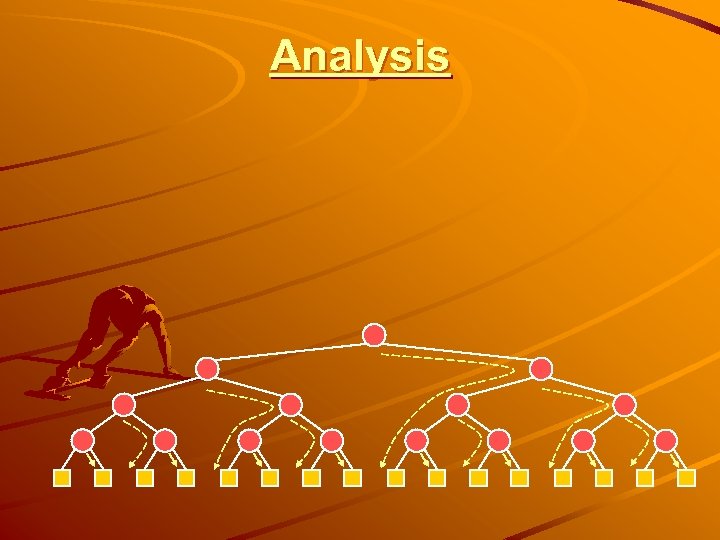
Analysis
Hash Functions
Hash Code Maps
Hash Code Maps (cont. )
Compression Maps
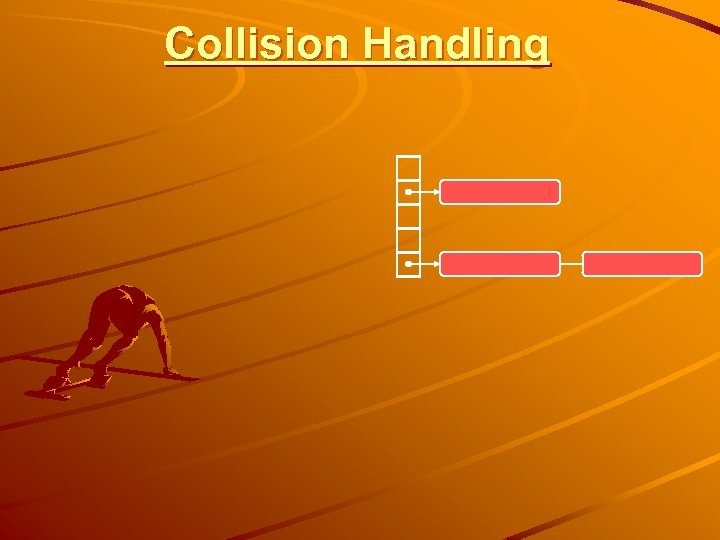
Collision Handling
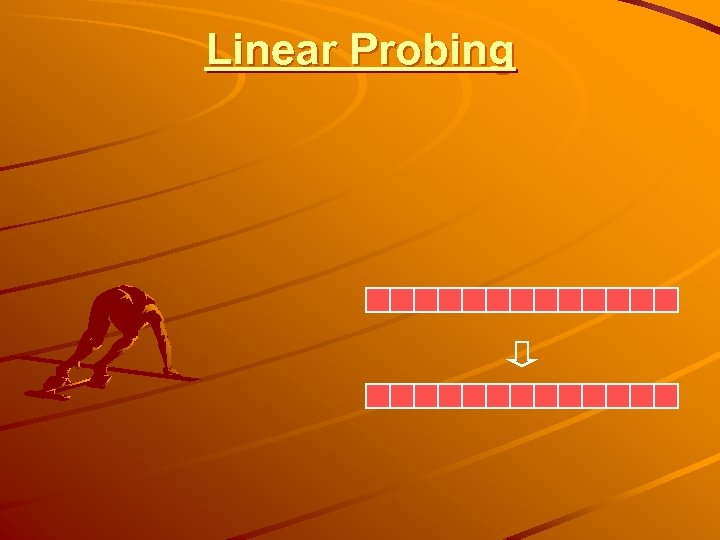
Linear Probing
Search with Linear Probing
Updates with Linear Probing
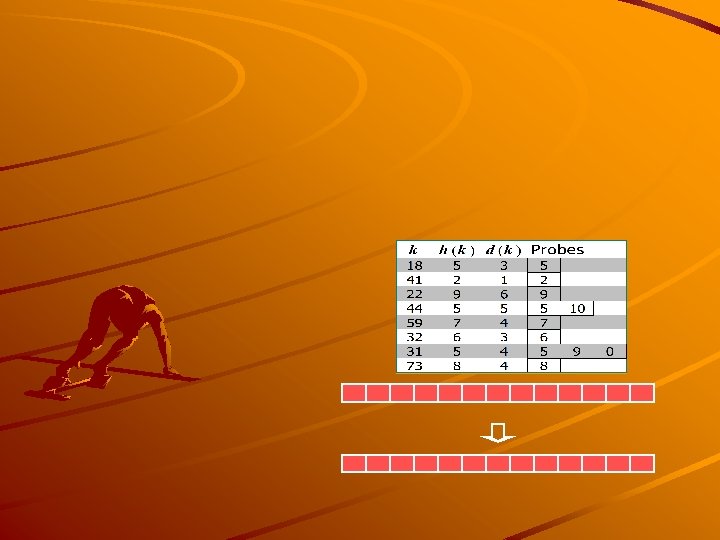
Performance of Hashing
Universal Hashing
Proof of Universality (Part 1) Let f(k) = ak+b mod p Let g(k) = k mod N So h(k) = g(f(k)). f causes no collisions: So a(j-k) is a multiple of p But both are less than p So a(j-k) = 0. I. e. , j=k. (contradiction) Thus, f causes no collisions.
Proof of Universality (Part 2)
Скачать презентацию Abstract Data Types ADTs Array-based Stack
5fafb28380e5487b493a9501c4fab29d.ppt