Ab initio Thermodynamics and Structure-Property Relationships Axel van

Ab initio Thermodynamics and Structure-Property Relationships Axel van de Walle Applied Physics and Materials Science Department Engineering and Applied Sciences Division http: //www. its. caltech. edu/~avdw/

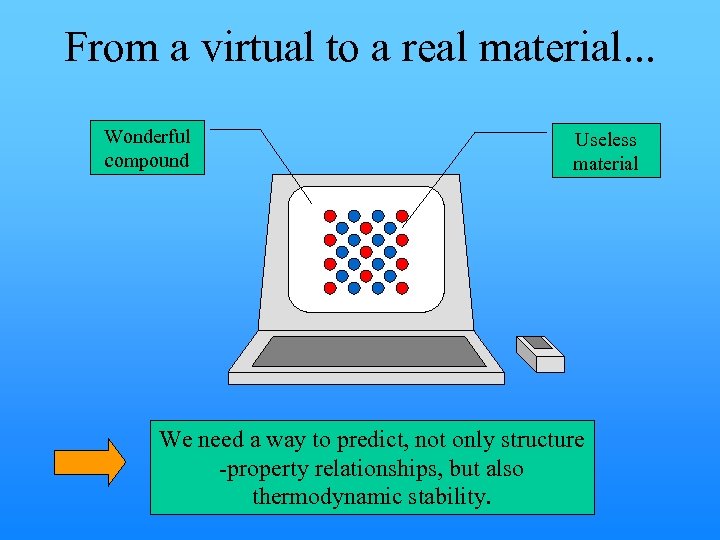
From a virtual to a real material. . . Wonderful compound Useless material We need a way to predict, not only structure -property relationships, but also thermodynamic stability.

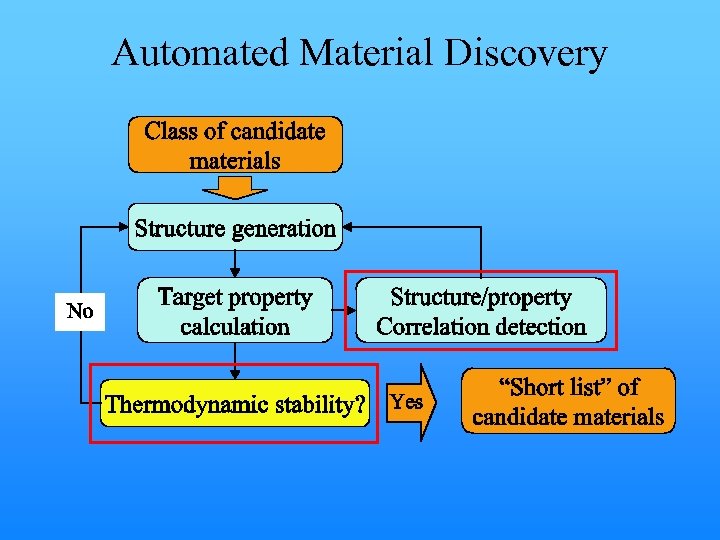
Automated Material Discovery

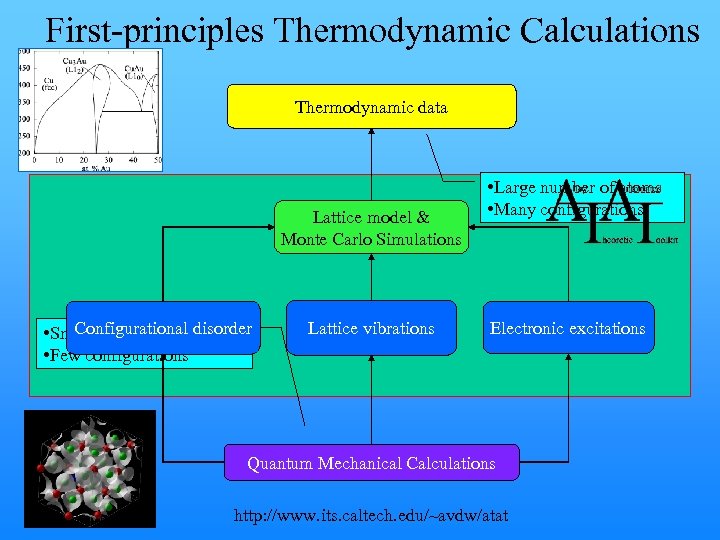
First-principles Thermodynamic Calculations Thermodynamic data Lattice model & Monte Carlo Simulations Configurational disorder • Small number of atoms • Few configurations Lattice vibrations • Large number of atoms • Many configurations Electronic excitations Quantum Mechanical Calculations http: //www. its. caltech. edu/~avdw/atat

Thermodynamic data Lattice model & Monte Carlo Simulations Electronic Lattice vibrations Configurational disorder excitations Configurational disorder Quantum Mechanical Calculations

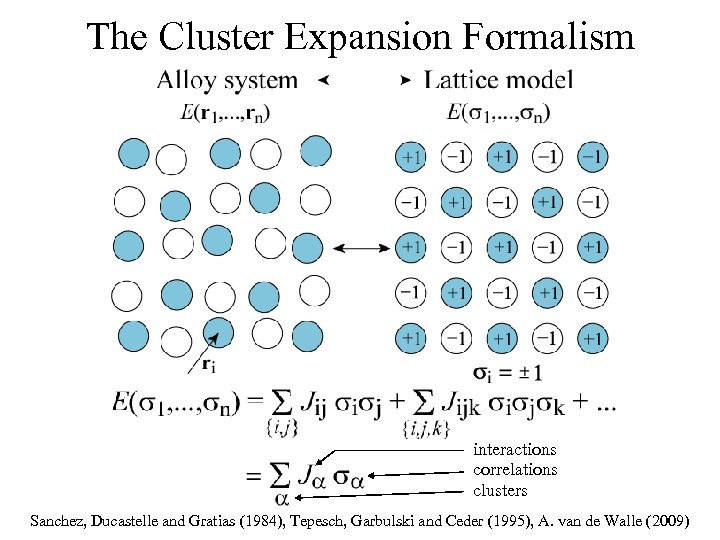
The Cluster Expansion Formalism interactions correlations clusters Sanchez, Ducastelle and Gratias (1984), Tepesch, Garbulski and Ceder (1995), A. van de Walle (2009)

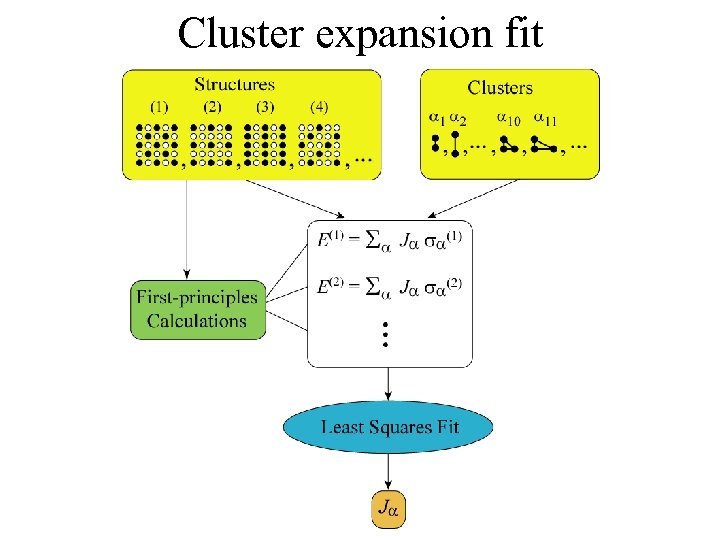
Cluster expansion fit

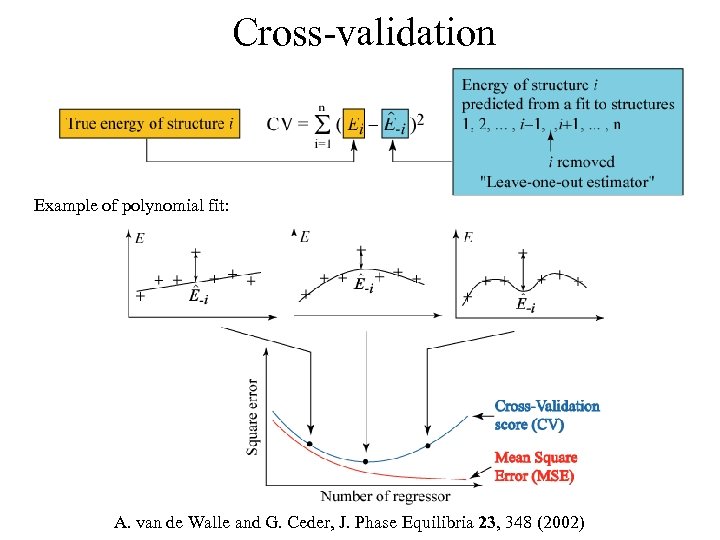
Cross-validation Example of polynomial fit: A. van de Walle and G. Ceder, J. Phase Equilibria 23, 348 (2002)

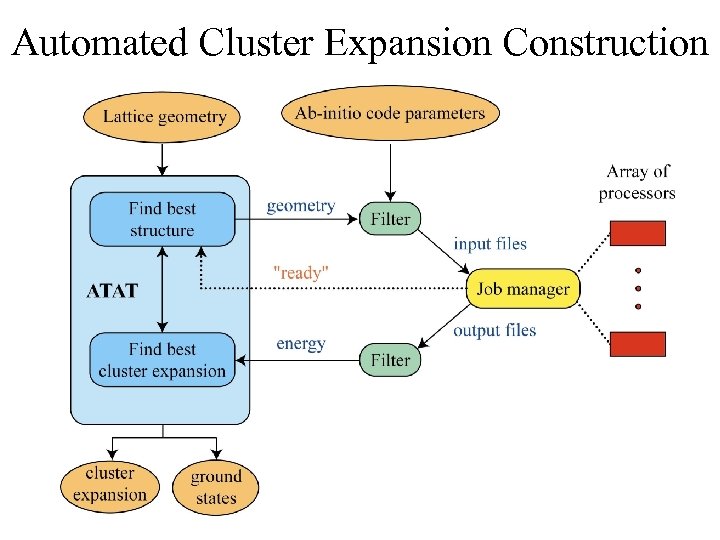
Automated Cluster Expansion Construction

Application Example • (Sm/Ce)O 2 Superlattices have been shown to exhibit enhanced Oxygen conductivity*. Cex. Sm 1 -x. Oy O ~50 nm • Goal: study interface thermodynamics to help understand origin of enhanced conductivity. *I. Kosackia, T. Christopher, M. Rouleau, P. F. Becher, J. Bentley, D. H. Lowndes, Solid State Ionics 176, 1319 (2005) and I. Kosacki, C. M. Rouleau, P. F. Becher and D. H. Lowndes, in press.

Convex hull construction E x[Ce] x[O]

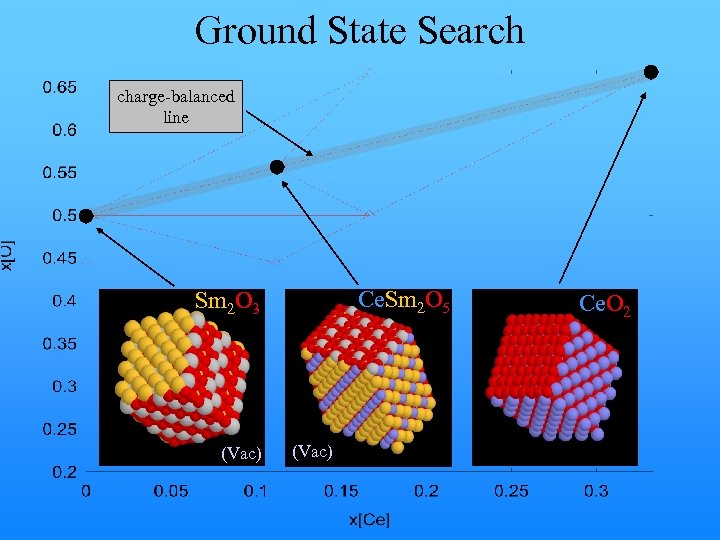
Ground State Search charge-balanced line Ce. Sm 2 O 5 Sm 2 O 3 (Vac) Ce. O 2

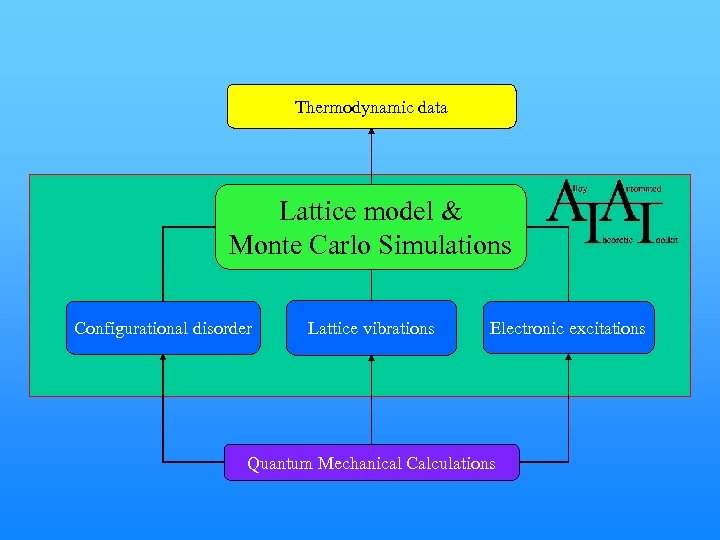
Thermodynamic data Lattice model & Monte Carlo Simulations Configurational disorder Lattice vibrations Electronic excitations Quantum Mechanical Calculations

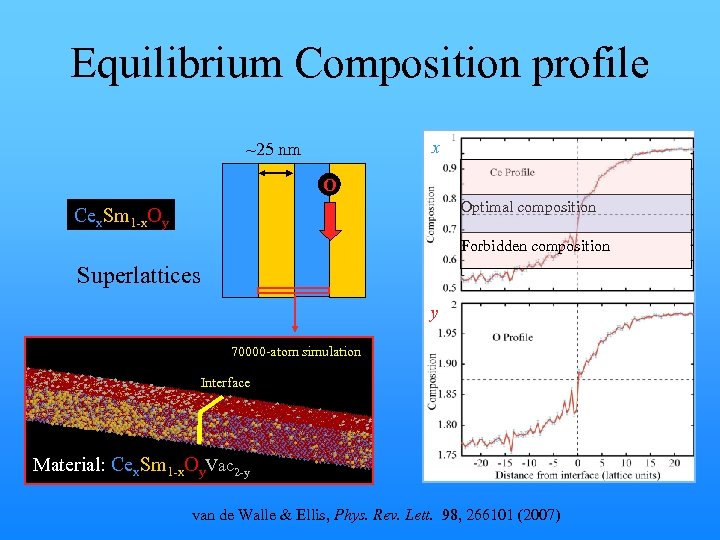
Equilibrium Composition profile x ~25 nm O Optimal composition Cex. Sm 1 -x. Oy Forbidden composition Superlattices y 70000 -atom simulation Interface Material: Cex. Sm 1 -x. Oy. Vac 2 -y van de Walle & Ellis, Phys. Rev. Lett. 98, 266101 (2007)

Application to Ti-Al Alloys Antiphase Boundary Diffuse Antiphase Boundary Creation of a plane with easy dislocation motion: Work softening

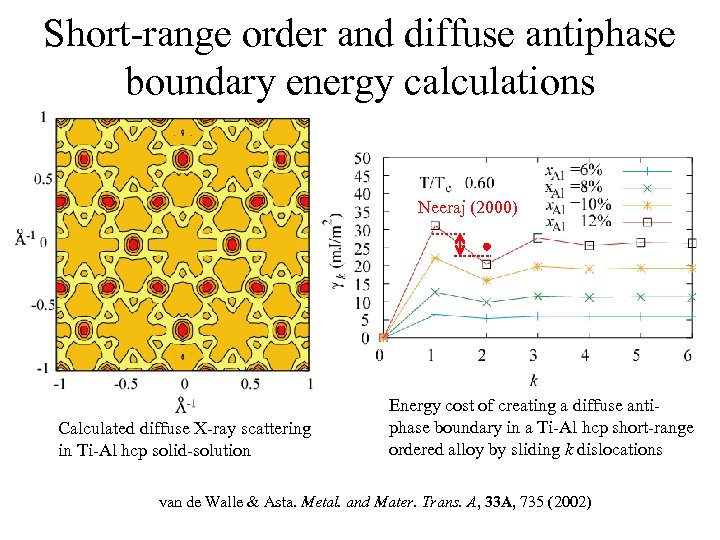
Short-range order and diffuse antiphase boundary energy calculations Neeraj (2000) Calculated diffuse X-ray scattering in Ti-Al hcp solid-solution Energy cost of creating a diffuse antiphase boundary in a Ti-Al hcp short-range ordered alloy by sliding k dislocations van de Walle & Asta. Metal. and Mater. Trans. A, 33 A, 735 (2002)

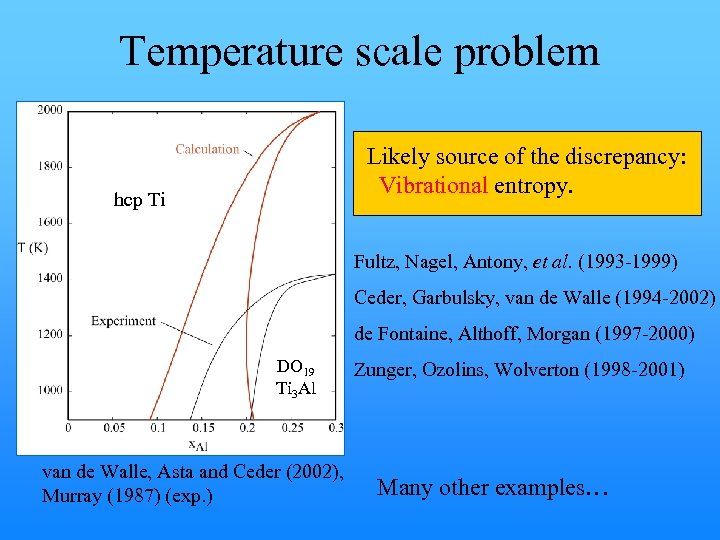
Temperature scale problem Likely source of the discrepancy: Vibrational entropy. hcp Ti Fultz, Nagel, Antony, et al. (1993 -1999) Ceder, Garbulsky, van de Walle (1994 -2002) de Fontaine, Althoff, Morgan (1997 -2000) DO 19 Ti 3 Al van de Walle, Asta and Ceder (2002), Murray (1987) (exp. ) Zunger, Ozolins, Wolverton (1998 -2001) Many other examples…

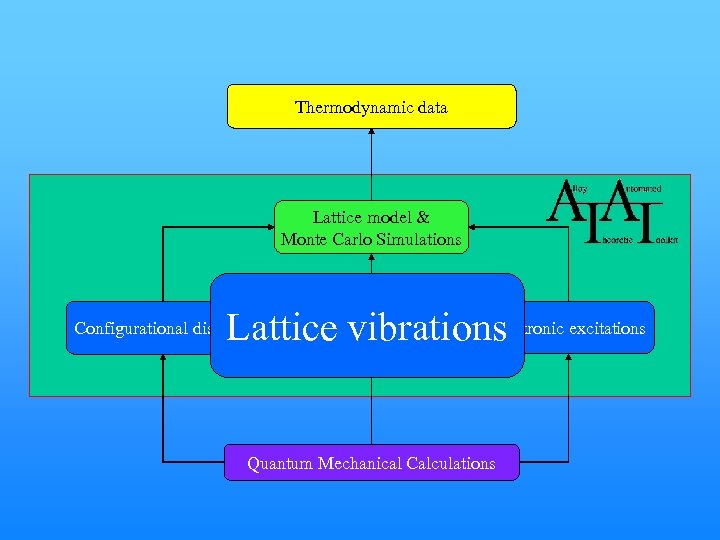
Thermodynamic data Lattice model & Monte Carlo Simulations Electronic excitations Lattice vibrations Configurational disorder Quantum Mechanical Calculations

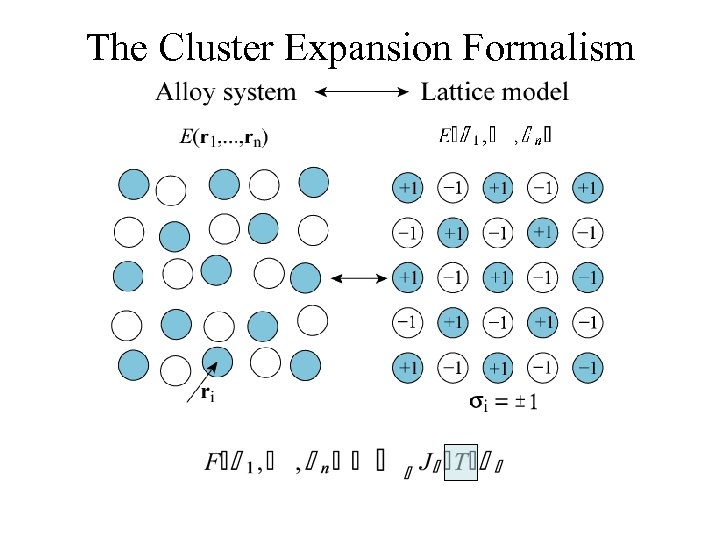
The Cluster Expansion Formalism

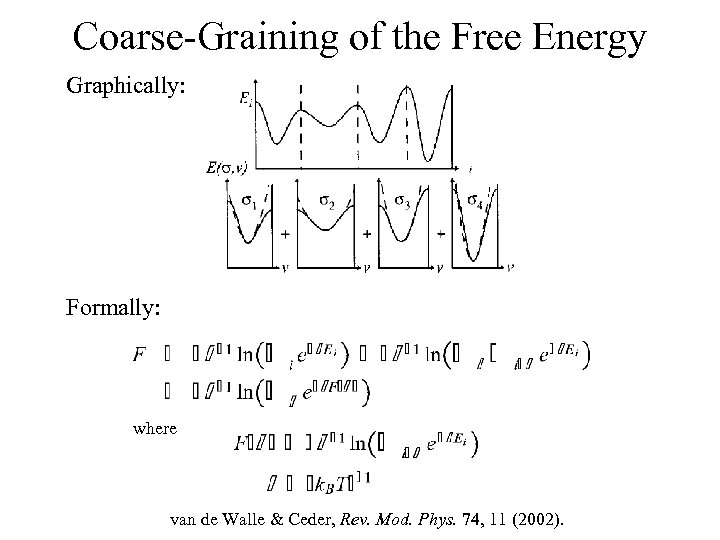
Coarse-Graining of the Free Energy Graphically: Formally: where van de Walle & Ceder, Rev. Mod. Phys. 74, 11 (2002).

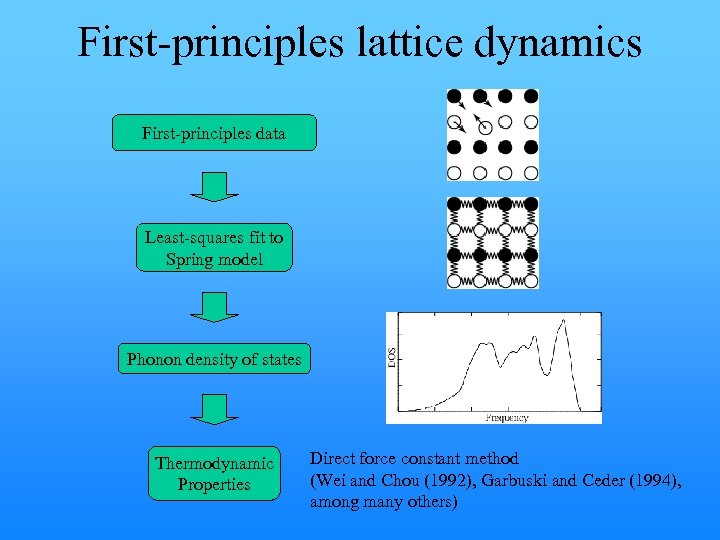
First-principles lattice dynamics First-principles data Least-squares fit to Spring model Phonon density of states Thermodynamic Properties Direct force constant method (Wei and Chou (1992), Garbuski and Ceder (1994), among many others)

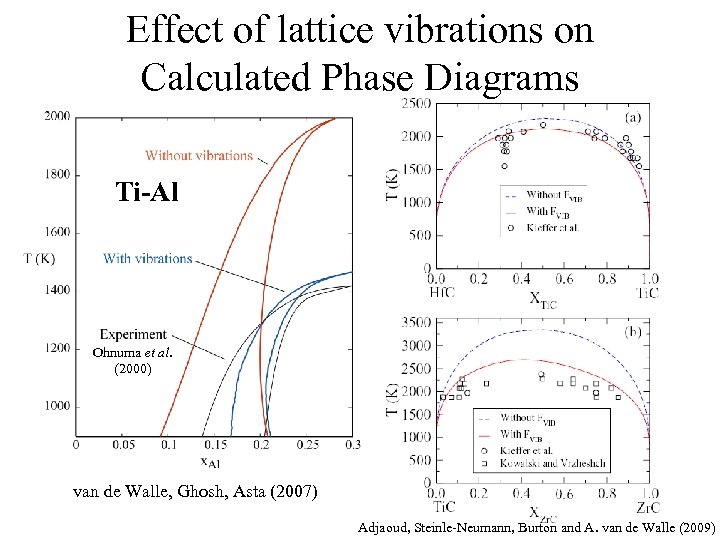
Effect of lattice vibrations on Calculated Phase Diagrams Ti-Al Ohnuma et al. (2000) van de Walle, Ghosh, Asta (2007) Adjaoud, Steinle-Neumann, Burton and A. van de Walle (2009)

Beyond the cluster expansion…

Surface reconstruction problem Example: Sr. Ti. O 3 (100) c(6 x 2) surface (Applications: Catalyst, Gate oxide in integrated circuits, Substrate for thin-film growth) ? O Known “bulk” crystal structure Sr Ti Solution: Combine experimental and computational methods Lanier, van de Walle, Erdman, Landree, Warschkow, Kazimirov, Poeppelmeier, Zegenhagen , Asta, Marks, Phys. Rev. B 76, 045421 (2007)

$Automated Screening Sr, Ti coordinates from e- and X-ray diffraction Locate candidate O sites$

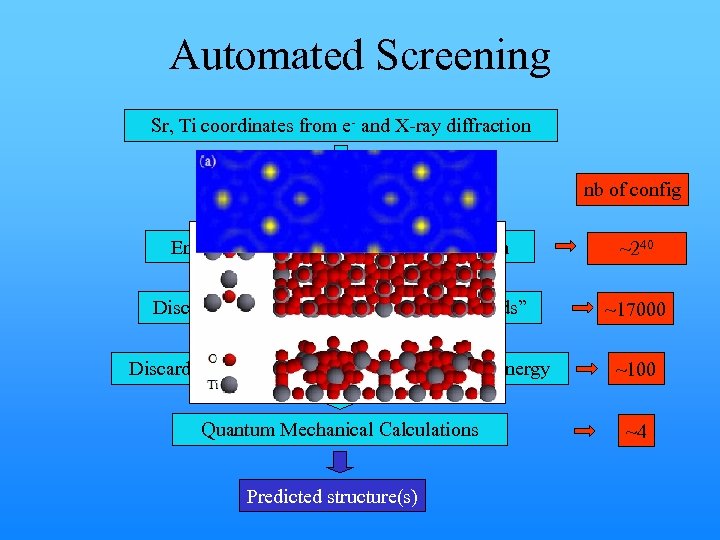
Automated Screening Sr, Ti coordinates from e- and X-ray diffraction Locate candidate O sites nb of config Enumerate every possible O configuration ~240 Discard configurations with “too many bonds” ~17000 Discard configuration with large electrostatic energy ~100 Quantum Mechanical Calculations ~4 Predicted structure(s)

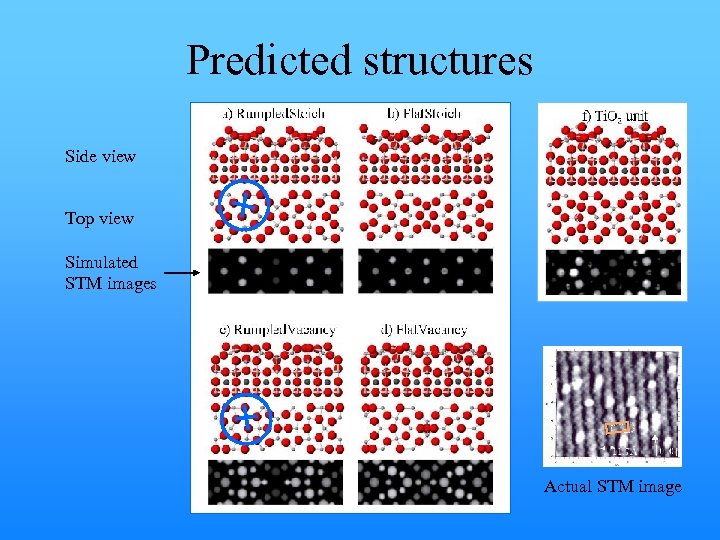
Predicted structures Side view Top view Simulated STM images Actual STM image

“The” equilibrium reconstruction of the Sr. Ti. O 3 (100) c(6 x 2) surface • A dynamic random “solid solution” of many different atomic motifs. • Each structure enters the refined model with fractional occupation. • Solved an exceptionally complex surface reconstruction problem!

Thermoelectrics: Phase stability in the Zn-Sb system • Zn-Sb has been of interest for many years in the search for efficient and low-cost thermoelectric materials: – Environmentally benign and relatively abundant elements – “Zn 4 Sb 3” phase exhibits a high thermoelectric efficiency. • However the “Zn 4 Sb 3” phase has a positive formation energy (20 me. V/atom): – is it really thermodynamically stable? – if so, why? • Entropy could play a role! G. S. Pomrehn, E. S. Toberer, G. J. Snyder & A. van de Walle, PRB (2011, forthcoming).

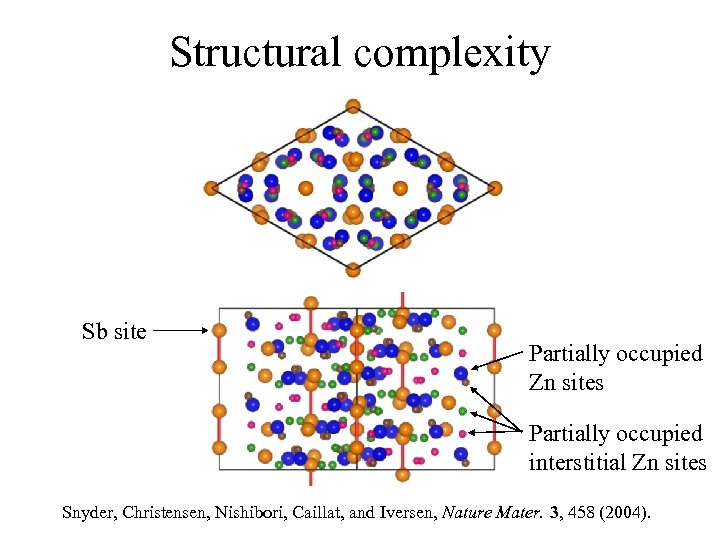
Structural complexity Sb site Partially occupied Zn sites Partially occupied interstitial Zn sites Snyder, Christensen, Nishibori, Caillat, and Iversen, Nature Mater. 3, 458 (2004).

Computational Method Independent cell approximation (works well if cell is big): + + + +

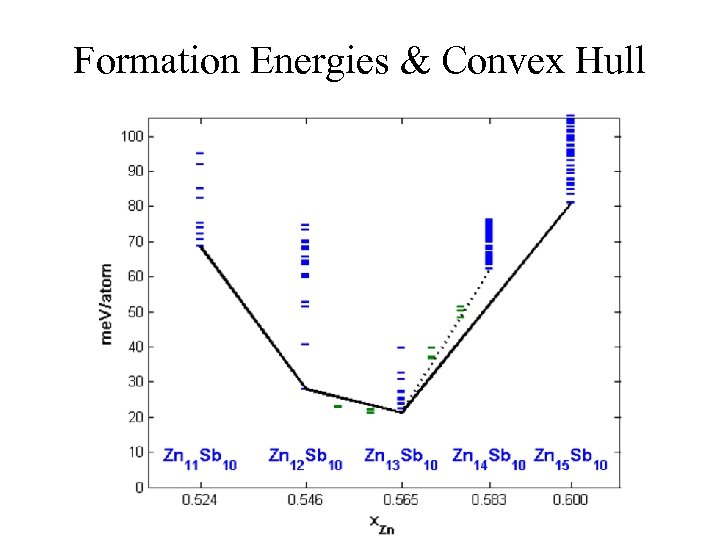
Formation Energies & Convex Hull

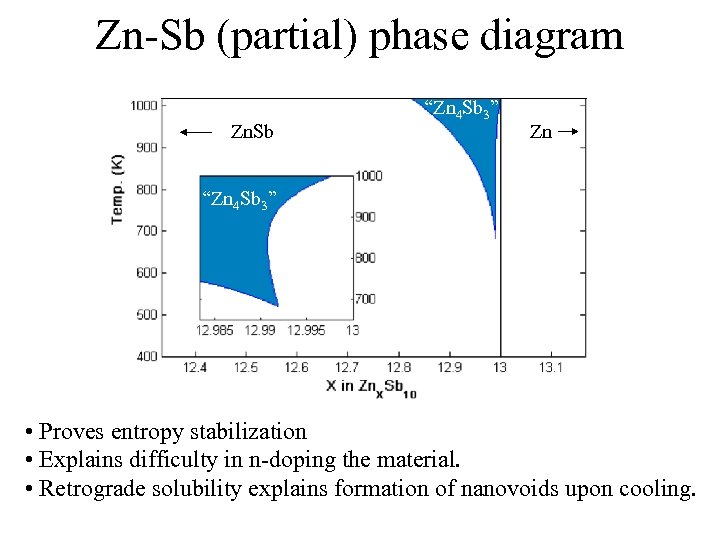
Zn-Sb (partial) phase diagram Zn. Sb “Zn 4 Sb 3” Zn “Zn 4 Sb 3” • Proves entropy stabilization • Explains difficulty in n-doping the material. • Retrograde solubility explains formation of nanovoids upon cooling.

Materials optimization for epitaxial optoelectronic device design • Essential features – Anisotropy – Experimental control over structure • Goal: – Guide experimental efforts to produce high-performance solar cells and LEDs. Nasser et al. (1999)

Structure-Property Relationships • Goal: Relate atomic-level structure to macroscopic properties. • For scalar properties of crystalline alloys, tool already exists: The Cluster Expansion. • Used for representing the structural dependence of – – – – bulk modulus equation of state phonon entropy electronic density of state band gap defect level energy Currie temperature M. Asta, R. Mc. Cormack, and D. de Fontaine (1993) H. Y. Geng, M. H. F. Sluiter, and N. X. Chen, (2005) G. D. Garbulsky and G. Ceder, (1994). H. Y. Geng, M. H. F. Sluiter, and N. X. Chen, (2005). A. Franceschetti and A. Zunger (1999). S. V. Dudiy and A. Zunger (2006). A. Franceschetti et al (2006). • The cluster expansion forms a basis for scalar functions of configurations.

The Tensorial Cluster Expansion • Needed to express configurational-dependence of many important properties in epitaxial systems: – – – – elastic constants, equilibrium strain/stress dielectric constant carrier effective masses ferroelectric vector piezoelectric tensor strain-gap coupling optoelectric coupling, etc. A. van de Walle, Nature materials 7, 455 (2008)

Bases and Tensors

“Tensor-product” basis binary case

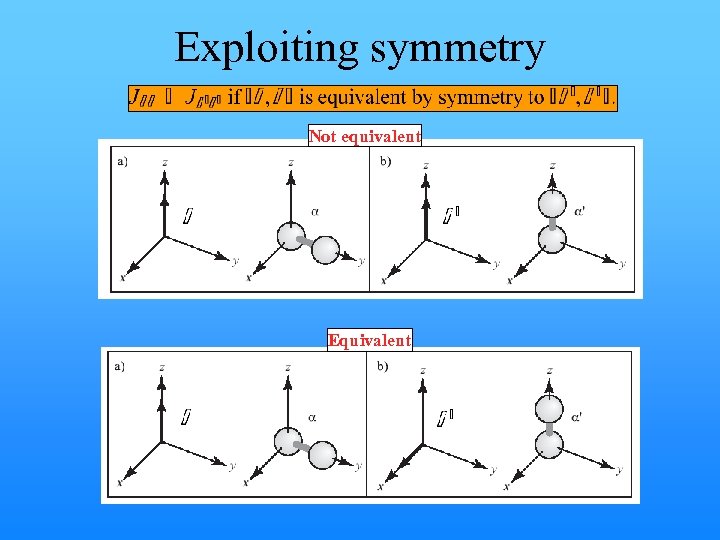
Exploiting symmetry Not equivalent Equivalent

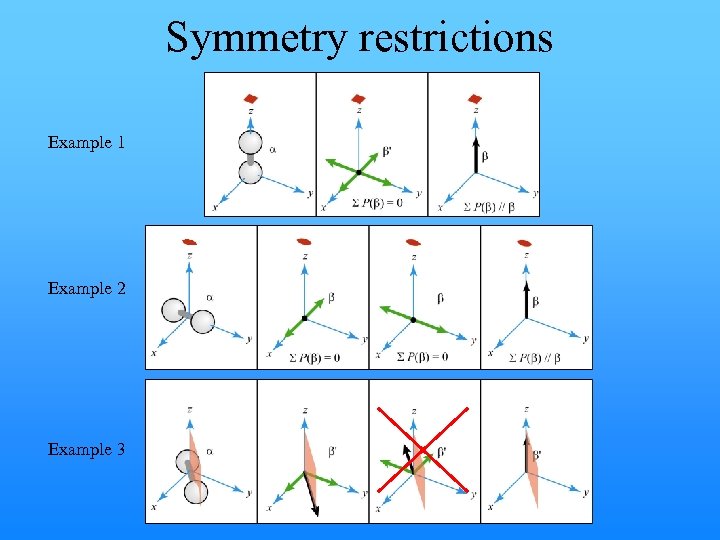
Symmetry restrictions Example 1 Example 2 Example 3

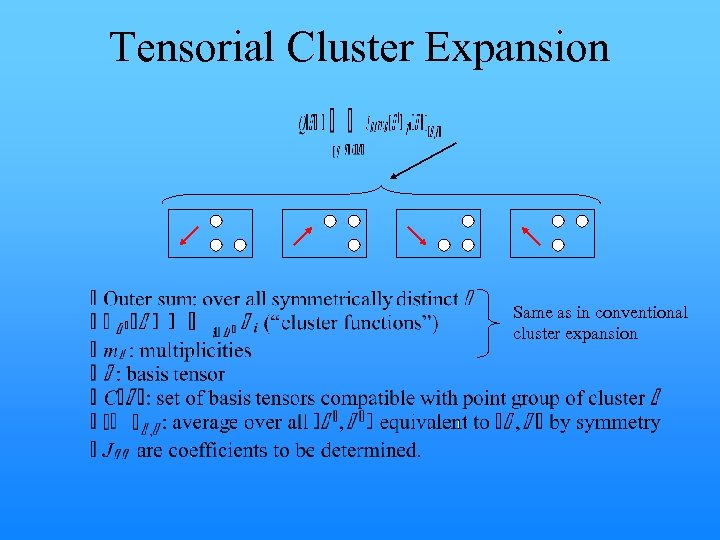
Tensorial Cluster Expansion Same as in conventional cluster expansion

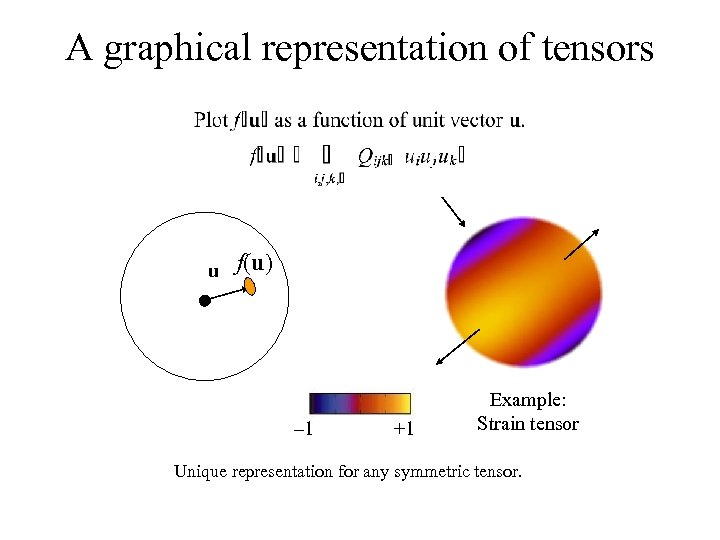
A graphical representation of tensors u f(u) – 1 +1 Example: Strain tensor Unique representation for any symmetric tensor.

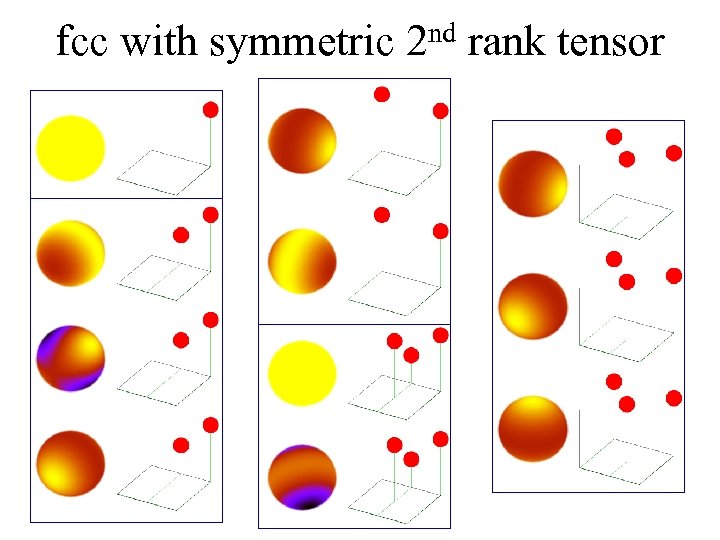
fcc with symmetric 2 nd rank tensor

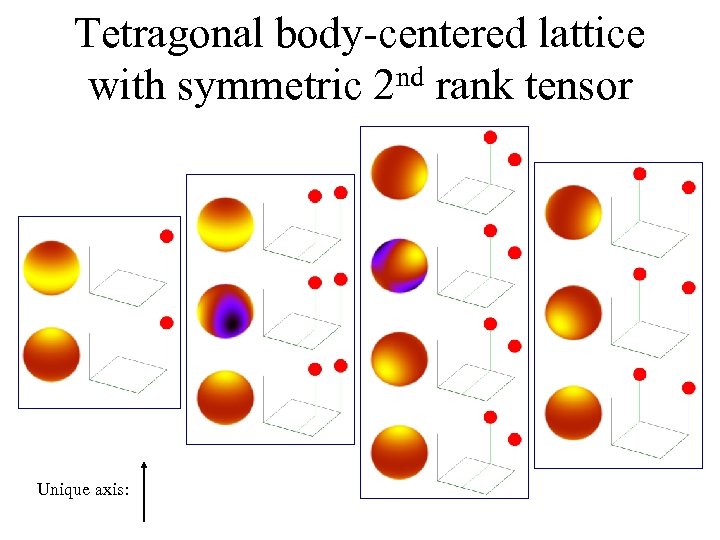
Tetragonal body-centered lattice with symmetric 2 nd rank tensor Unique axis:

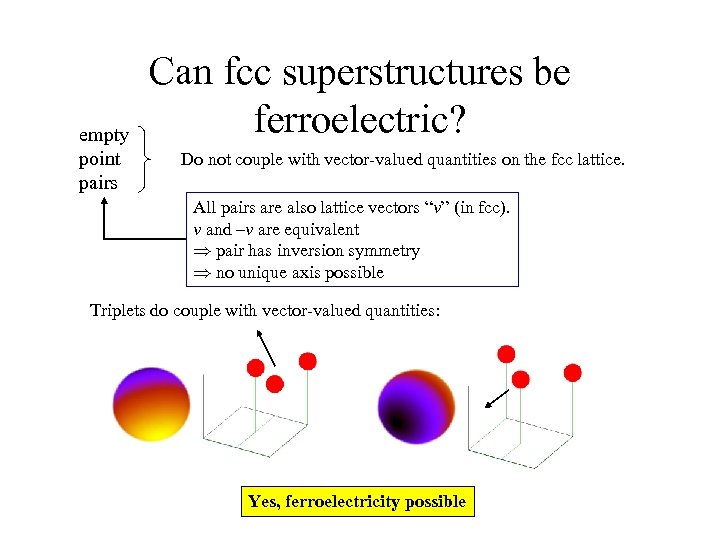
empty point pairs Can fcc superstructures be ferroelectric? Do not couple with vector-valued quantities on the fcc lattice. All pairs are also lattice vectors “v” (in fcc). v and –v are equivalent Þ pair has inversion symmetry Þ no unique axis possible Triplets do couple with vector-valued quantities: Yes, ferroelectricity possible

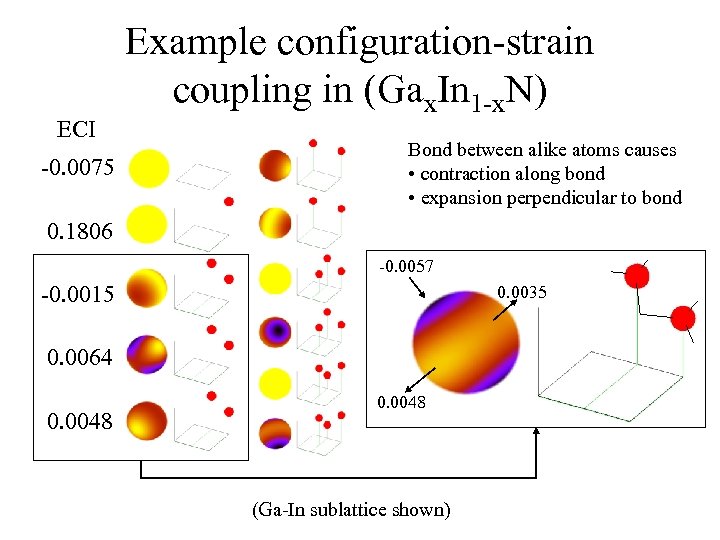
ECI -0. 0075 Example configuration-strain coupling in (Gax. In 1 -x. N) Bond between alike atoms causes • contraction along bond • expansion perpendicular to bond 0. 1806 -0. 0057 -0. 0015 0. 0035 0. 0064 0. 0048 (Ga-In sublattice shown)

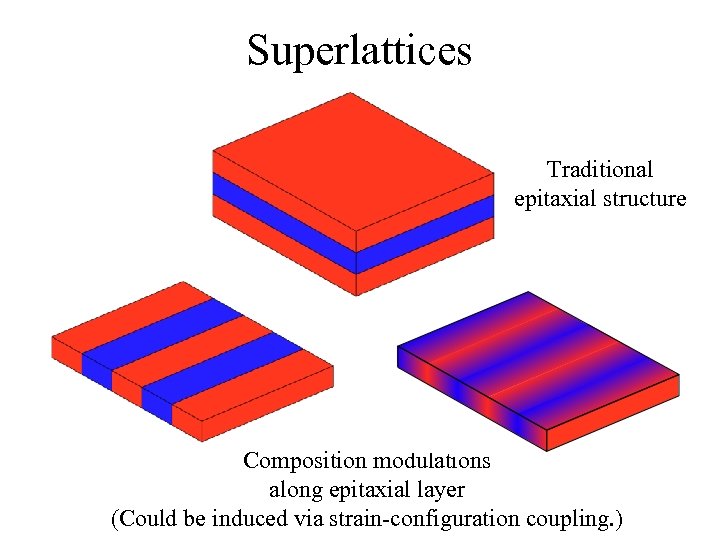
Superlattices Traditional epitaxial structure Composition modulations along epitaxial layer (Could be induced via strain-configuration coupling. )

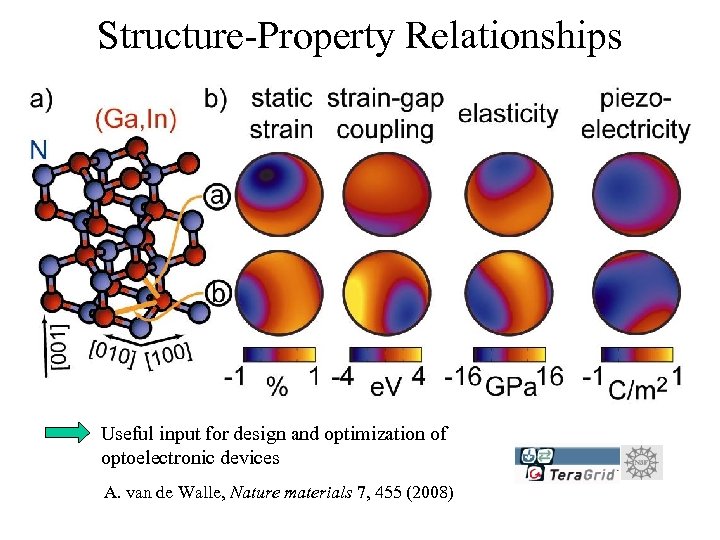
Structure-Property Relationships Useful input for design and optimization of optoelectronic devices A. van de Walle, Nature materials 7, 455 (2008)

Conclusion & outlook • Ab initio materials design is becoming a reality and requires – methods to assess phase stability – methods to uncover structure-property relationships • There is the need to develop methods that break free of the “known lattice” assumption.