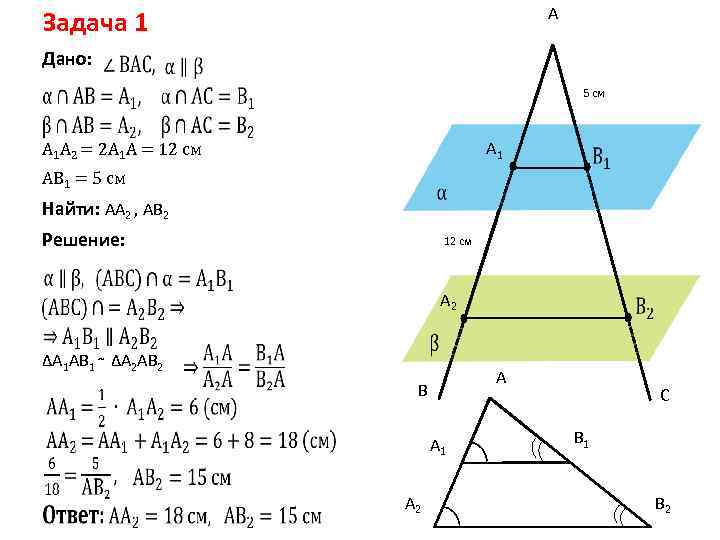
 A Задача 1 Дано: 5 см A 1 A 2 = 2 A 1 A = 12 см AB 1 = 5 см Найти: АА 2 , АВ 2 Решение: 12 см A 2 ∆А 1 АВ 1 ∼ ∆А 2 АВ 2 А B А 1 C В 1 А 2 B 2
A Задача 1 Дано: 5 см A 1 A 2 = 2 A 1 A = 12 см AB 1 = 5 см Найти: АА 2 , АВ 2 Решение: 12 см A 2 ∆А 1 АВ 1 ∼ ∆А 2 АВ 2 А B А 1 C В 1 А 2 B 2
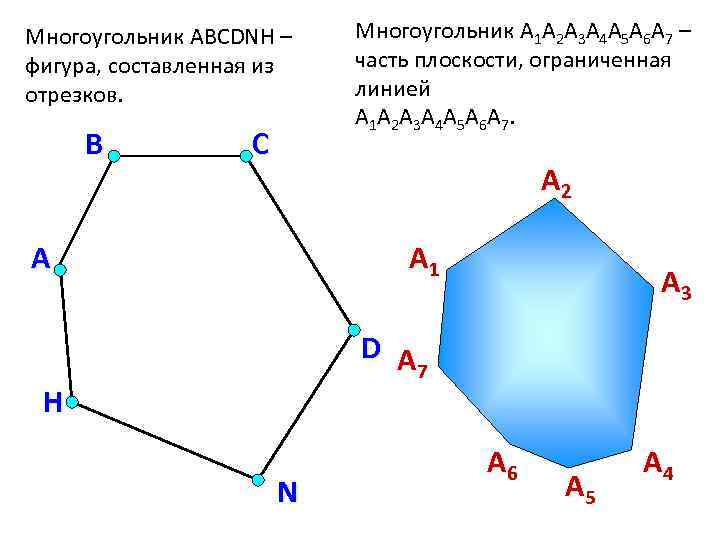 Многоугольник ABCDNH – фигура, составленная из отрезков. В С Многоугольник A 1 А 2 А 3 А 4 А 5 А 6 А 7 – часть плоскости, ограниченная линией A 1 А 2 А 3 А 4 А 5 А 6 А 7. А 2 А А 1 А 3 D А 7 H N А 6 А 5 А 4
Многоугольник ABCDNH – фигура, составленная из отрезков. В С Многоугольник A 1 А 2 А 3 А 4 А 5 А 6 А 7 – часть плоскости, ограниченная линией A 1 А 2 А 3 А 4 А 5 А 6 А 7. А 2 А А 1 А 3 D А 7 H N А 6 А 5 А 4
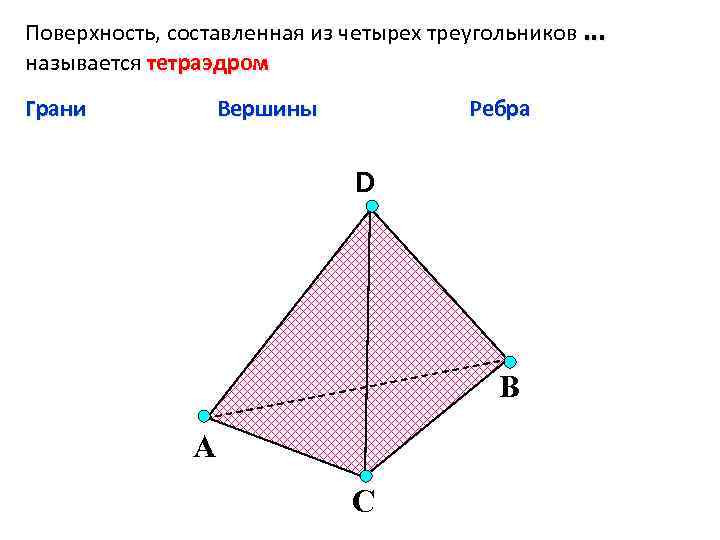 Поверхность, составленная из четырех треугольников … называется тетраэдром Грани Вершины Ребра D В А С
Поверхность, составленная из четырех треугольников … называется тетраэдром Грани Вершины Ребра D В А С
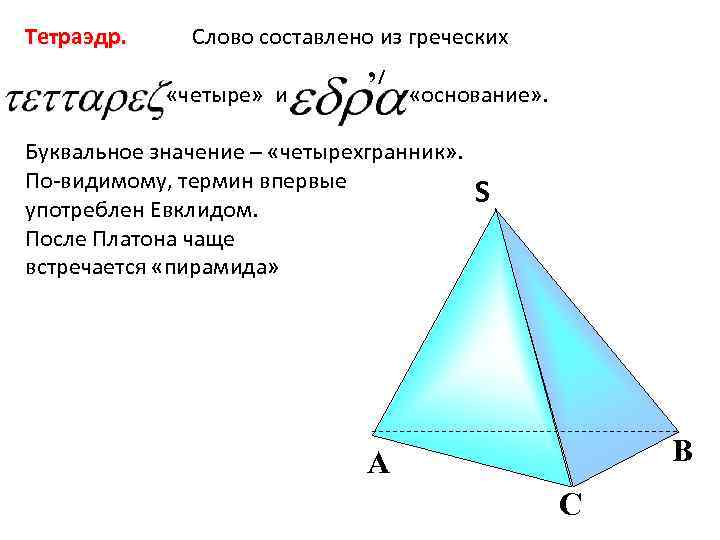 Тетраэдр. Слово составлено из греческих , / «четыре» и - «основание» . Буквальное значение – «четырехгранник» . По-видимому, термин впервые S S употреблен Евклидом. После Платона чаще встречается «пирамида» В А С
Тетраэдр. Слово составлено из греческих , / «четыре» и - «основание» . Буквальное значение – «четырехгранник» . По-видимому, термин впервые S S употреблен Евклидом. После Платона чаще встречается «пирамида» В А С
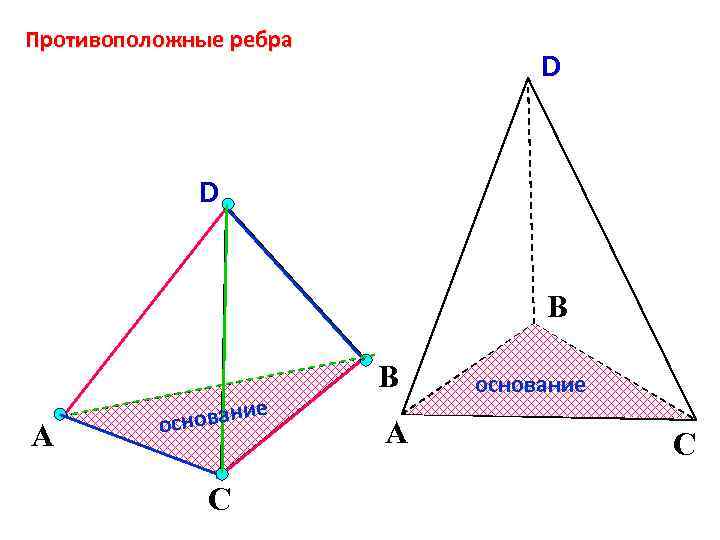 Противоположные ребра D D В А ование осн С В А основание С
Противоположные ребра D D В А ование осн С В А основание С
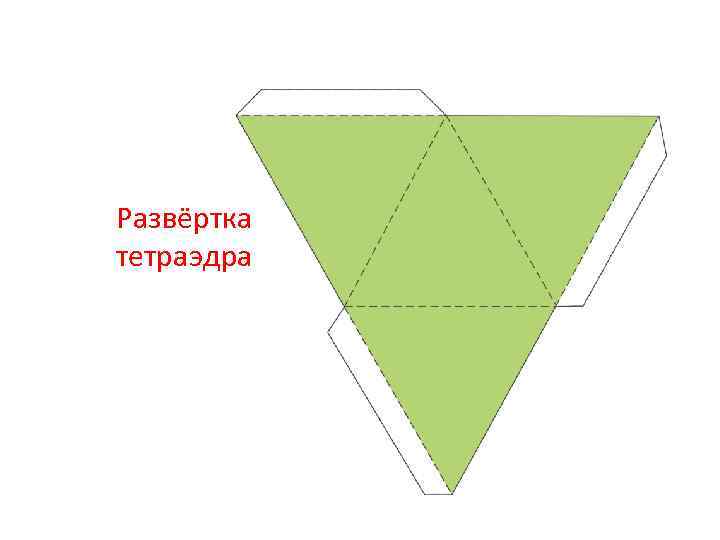 Развёртка тетраэдра
Развёртка тетраэдра
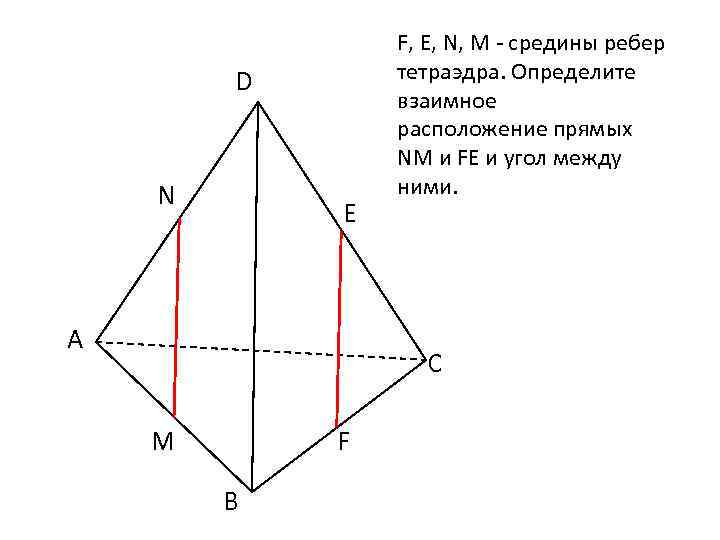 D N E А F, Е, N, M - средины ребер тетраэдра. Определите взаимное расположение прямых NM и FЕ и угол между ними. С M F В
D N E А F, Е, N, M - средины ребер тетраэдра. Определите взаимное расположение прямых NM и FЕ и угол между ними. С M F В
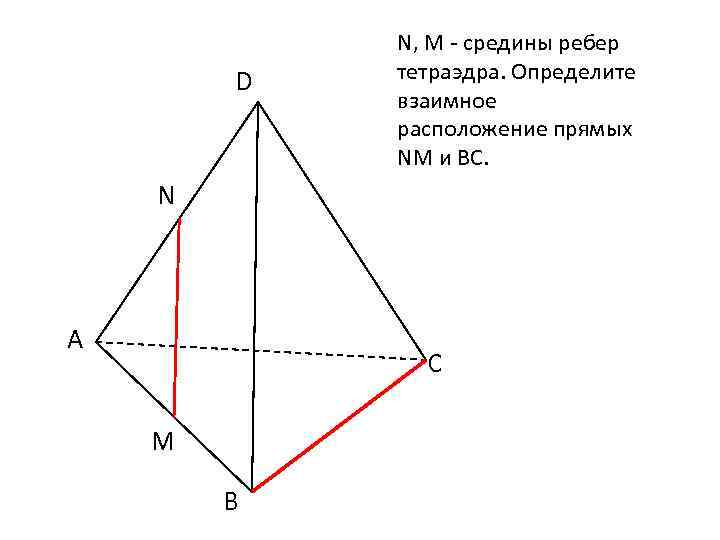 D N, M - средины ребер тетраэдра. Определите взаимное расположение прямых NM и ВС. N А С M В
D N, M - средины ребер тетраэдра. Определите взаимное расположение прямых NM и ВС. N А С M В
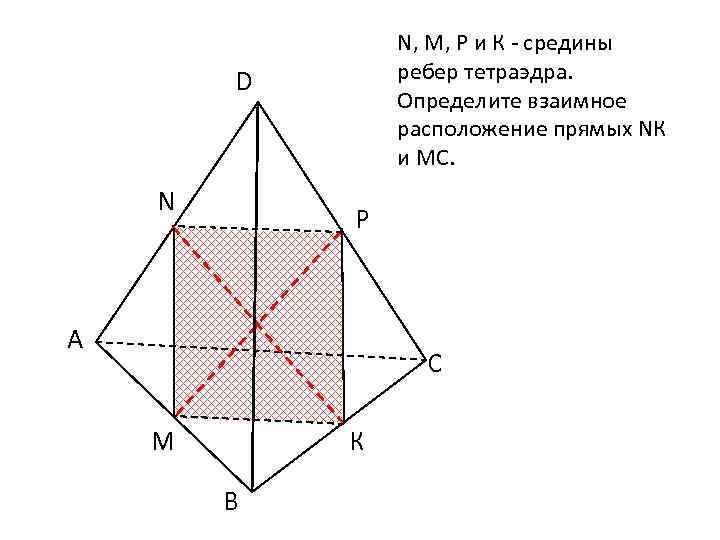 N, M, Р и К - средины ребер тетраэдра. Определите взаимное расположение прямых NК и МС. D N Р А С M К В
N, M, Р и К - средины ребер тетраэдра. Определите взаимное расположение прямых NК и МС. D N Р А С M К В
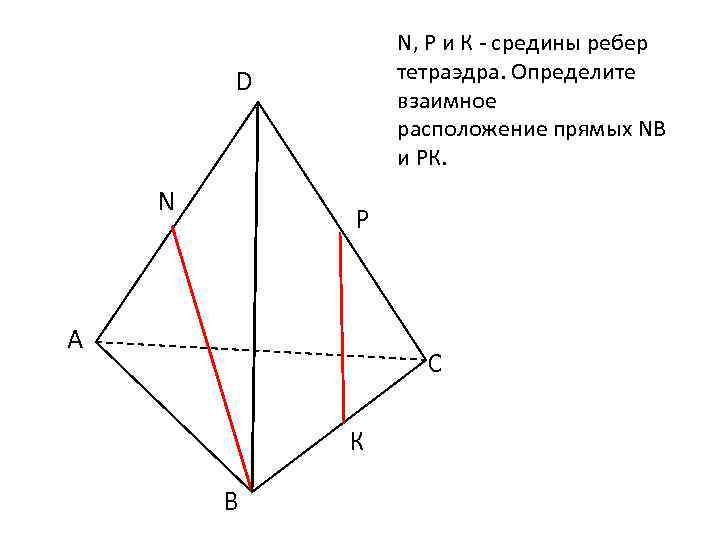 N, Р и К - средины ребер тетраэдра. Определите взаимное расположение прямых NВ и РК. D N Р А С К В
N, Р и К - средины ребер тетраэдра. Определите взаимное расположение прямых NВ и РК. D N Р А С К В
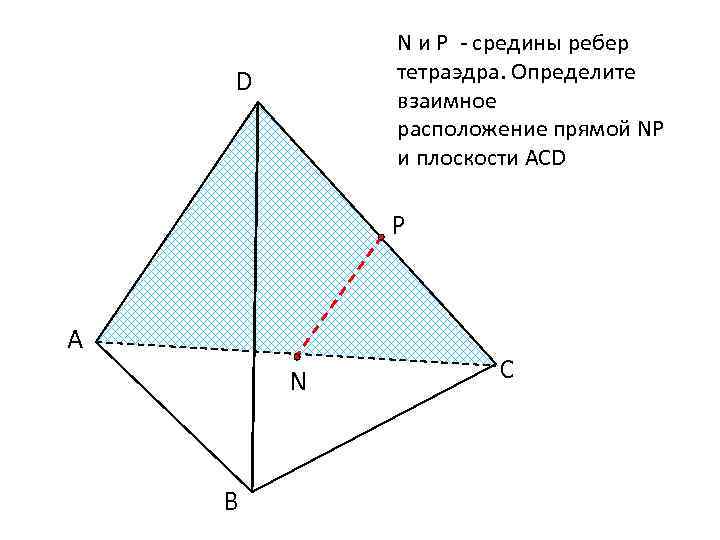 N и Р - средины ребер тетраэдра. Определите взаимное расположение прямой NР и плоскости АСD D Р А N В С
N и Р - средины ребер тетраэдра. Определите взаимное расположение прямой NР и плоскости АСD D Р А N В С
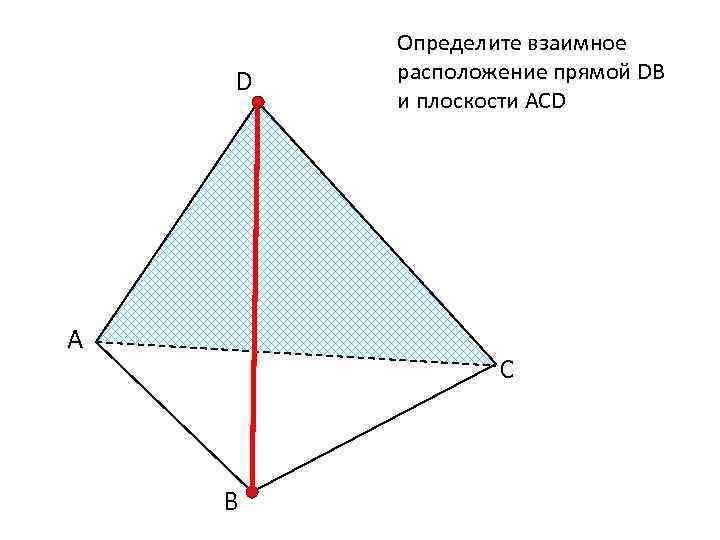 D А Определите взаимное расположение прямой DВ и плоскости АСD С В
D А Определите взаимное расположение прямой DВ и плоскости АСD С В
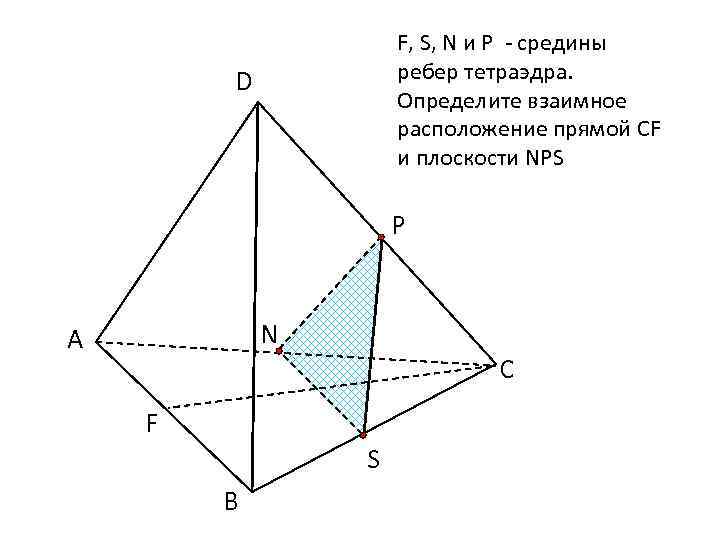 F, S, N и Р - средины ребер тетраэдра. Определите взаимное расположение прямой CF и плоскости NPS D Р N А С F S В
F, S, N и Р - средины ребер тетраэдра. Определите взаимное расположение прямой CF и плоскости NPS D Р N А С F S В
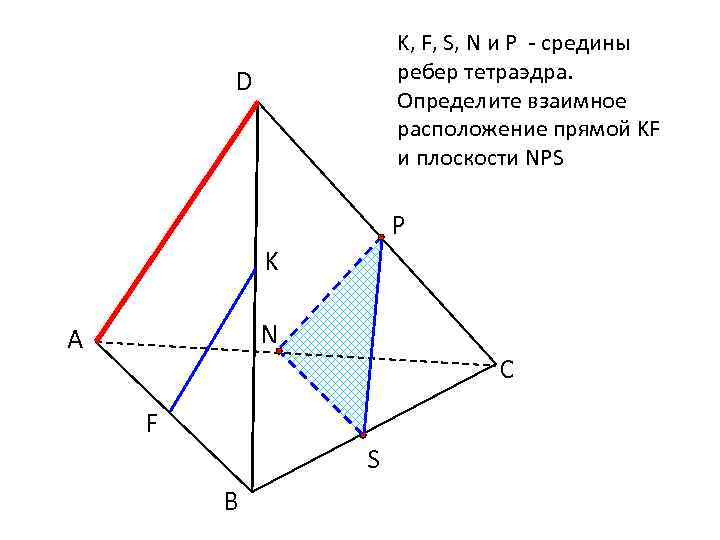 K, F, S, N и Р - средины ребер тетраэдра. Определите взаимное расположение прямой KF и плоскости NPS D Р K N А С F S В
K, F, S, N и Р - средины ребер тетраэдра. Определите взаимное расположение прямой KF и плоскости NPS D Р K N А С F S В
 № 73 А Дано: АВСD – тетраэдр, МА=МВ; ВN=NC; CP=PD; АК=КD; АС=10 см; BD=12 см; Доказать: Найти: Решение: M К В D N Р С
№ 73 А Дано: АВСD – тетраэдр, МА=МВ; ВN=NC; CP=PD; АК=КD; АС=10 см; BD=12 см; Доказать: Найти: Решение: M К В D N Р С
 Домашнее задание 1. п. 12 2. № 67(а); 70; 71(а) 3. Склеить тетраэдр
Домашнее задание 1. п. 12 2. № 67(а); 70; 71(а) 3. Склеить тетраэдр