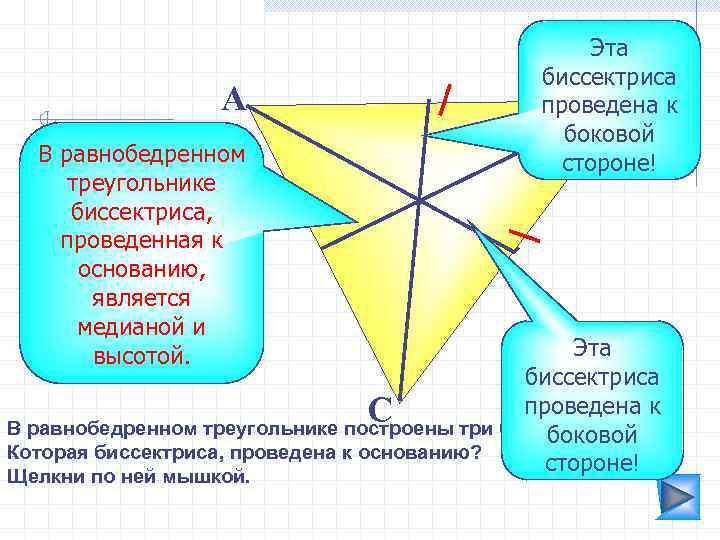
А В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. Эта биссектриса проведена к В боковой стороне! Эта биссектриса проведена к С В равнобедренном треугольнике построены три биссектрисы. боковой Которая биссектриса, проведена к основанию? стороне! Щелкни по ней мышкой.
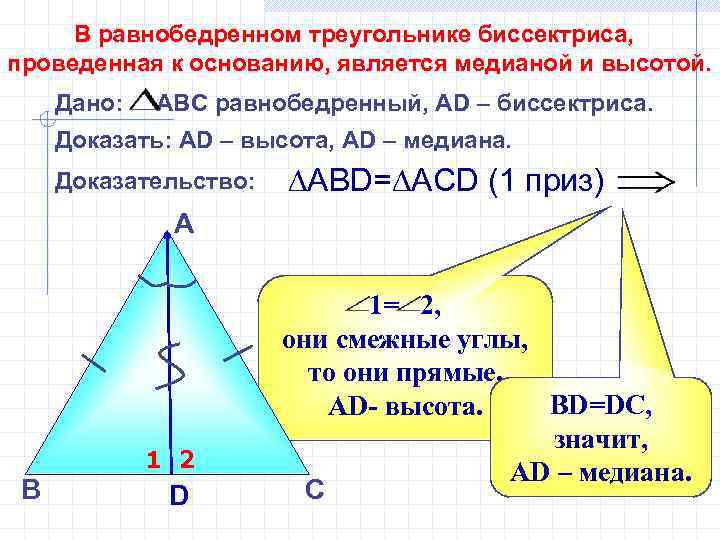
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой. Дано: АВС равнобедренный, АD – биссектриса. Доказать: АD – высота, АD – медиана. Доказательство: ∆АВD=∆АСD (1 приз) А 1 2 В D 1= 2, они смежные углы, то они прямые. ВD=DC, АD- высота. значит, АD – медиана. С
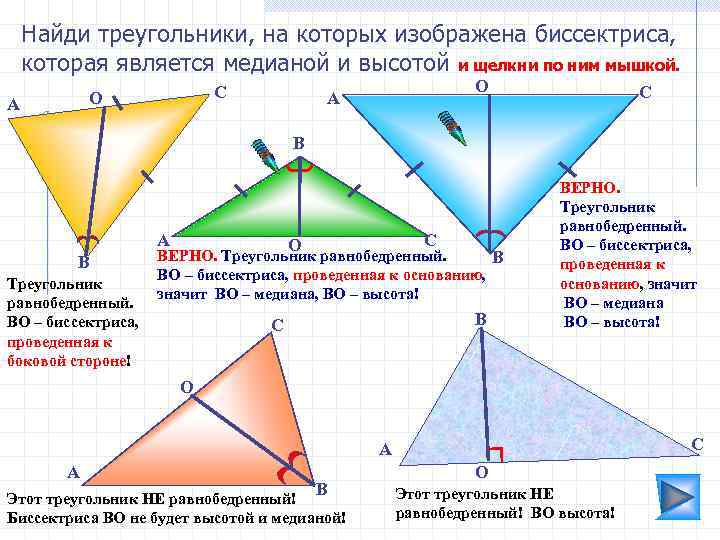
Найди треугольники, на которых изображена биссектриса, которая является медианой и высотой и щелкни по ним мышкой. С О А С В А В Треугольник равнобедренный. ВО – биссектриса, проведенная к боковой стороне! С О ВЕРНО. Треугольник равнобедренный. В ВО – биссектриса, проведенная к основанию, значит ВО – медиана, ВО – высота! В С ВЕРНО. Треугольник равнобедренный. ВО – биссектриса, проведенная к основанию, значит ВО – медиана ВО – высота! О С А А В Этот треугольник НЕ равнобедренный! Биссектриса ВО не будет высотой и медианой! О Этот треугольник НЕ равнобедренный! ВО высота!
Справедливы также утверждения 1. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой. 2. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
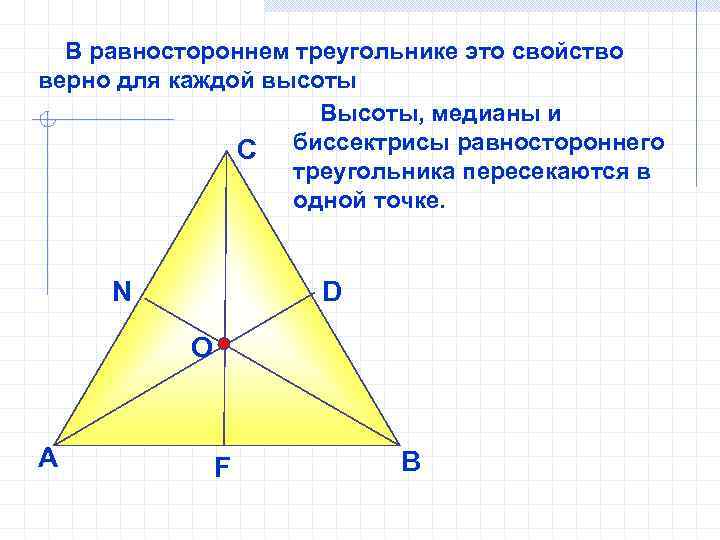
В равностороннем треугольнике это свойство верно для каждой высоты Высоты, медианы и С биссектрисы равностороннего треугольника пересекаются в одной точке. N D O А F В
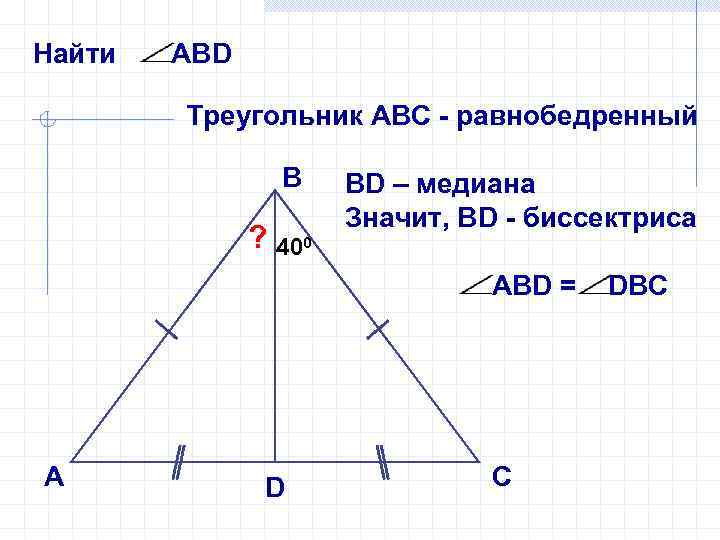
Найти АВD Треугольник АВС - равнобедренный В ? 400 ВD – медиана Значит, ВD - биссектриса АВD = А D С DВС
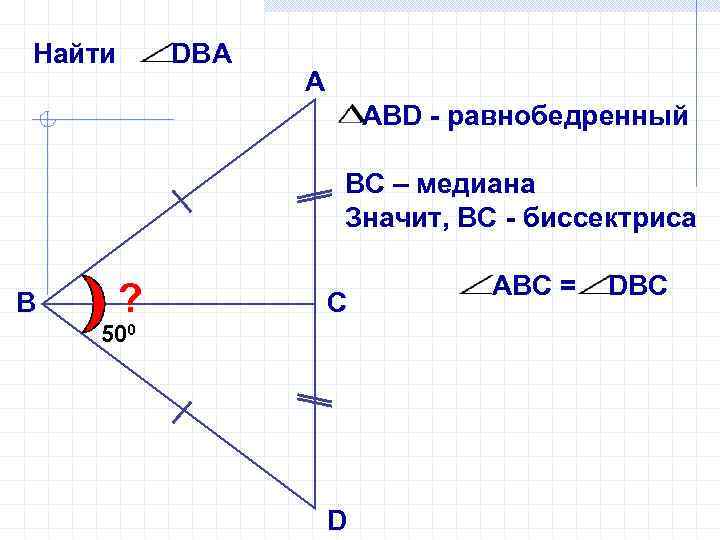
Найти DВА А АВD - равнобедренный ВС – медиана Значит, ВС - биссектриса В ? С 500 D АВС = DВС
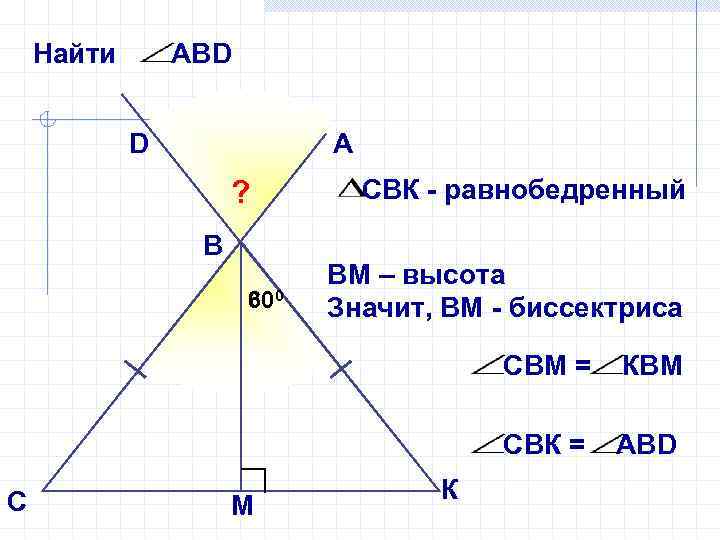
Найти АВD D А ? В 60 300 СВК - равнобедренный ВМ – высота Значит, ВМ - биссектриса СВМ = СВК = С М К КВМ АВD
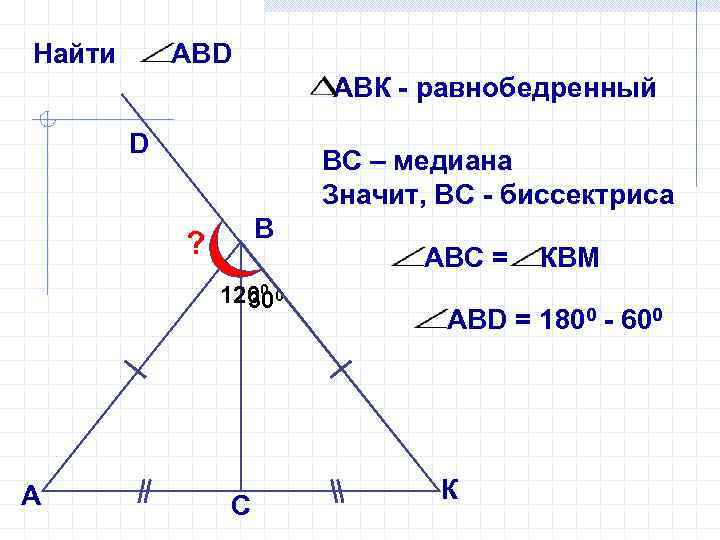
Найти АВD АВК - равнобедренный D ВС – медиана Значит, ВС - биссектриса В ? 1200 0 30 А С АВС = КВМ АВD = 1800 - 600 К
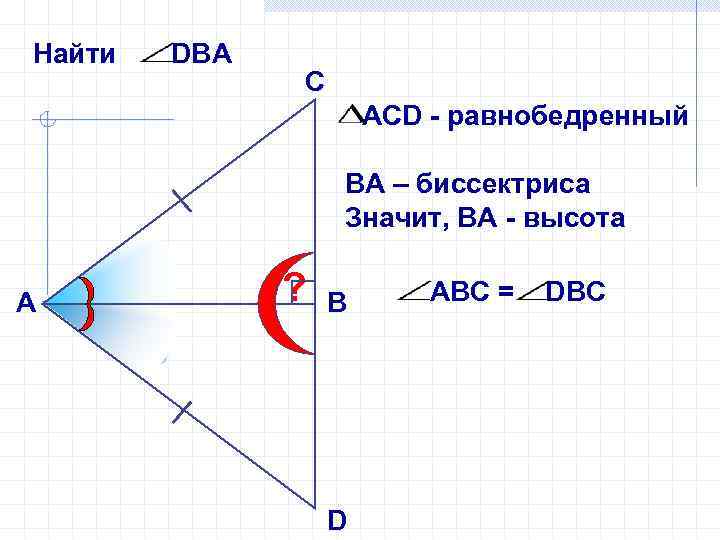
Найти DВА С АСD - равнобедренный ВА – биссектриса Значит, ВА - высота А ? В D АВС = DВС
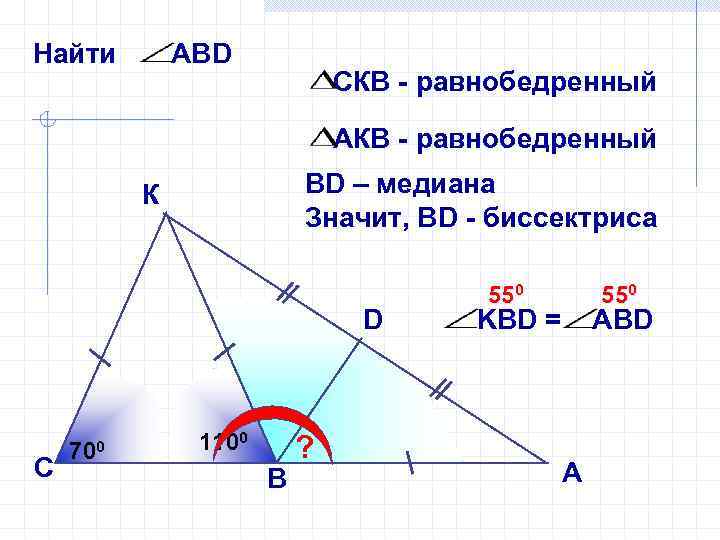
Найти АВD СКВ - равнобедренный АКВ - равнобедренный ВD – медиана Значит, ВD - биссектриса К D С 700 1100 В ? 550 KBD = ABD А
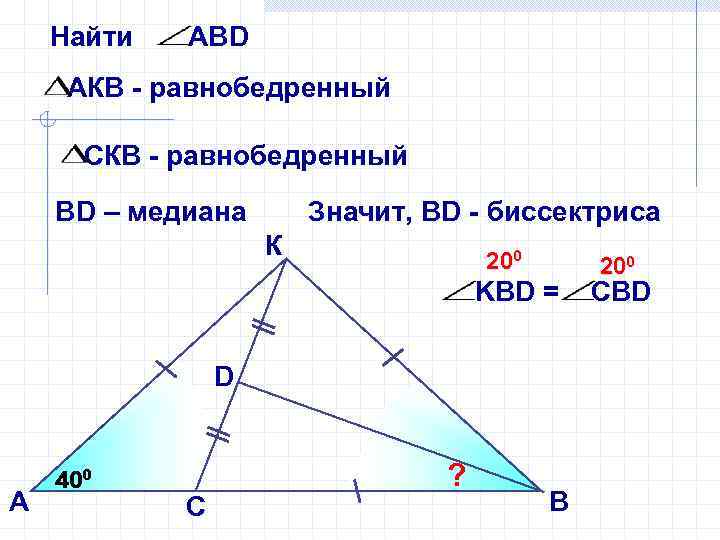
Найти АВD АКВ - равнобедренный СКВ - равнобедренный ВD – медиана Значит, ВD - биссектриса К 200 KBD = D А 400 С ? В 200 СBD
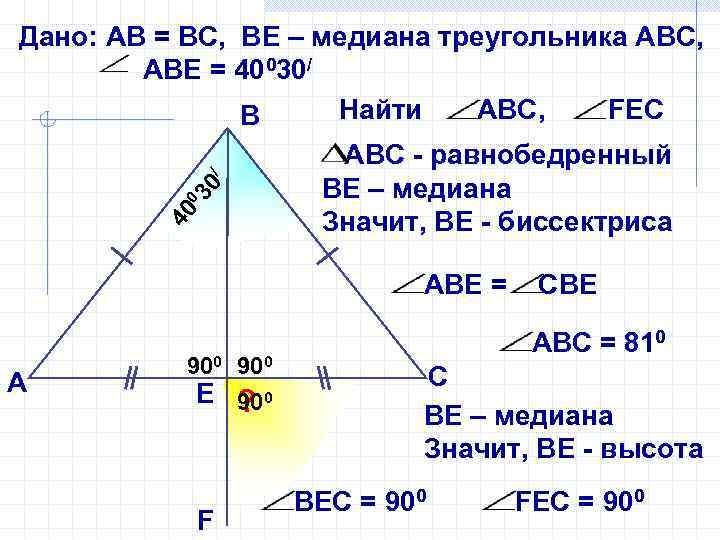
40 0 30 / Дано: АВ = ВС, ВЕ – медиана треугольника АВС, АВЕ = 40030/ Найти АВС, FEC В АВC - равнобедренный ВЕ – медиана Значит, ВЕ - биссектриса АВЕ = А 900 Е ? 0 90 F СВЕ АВС = 810 С ВЕ – медиана Значит, ВЕ - высота ВЕС = 900 FЕС = 900
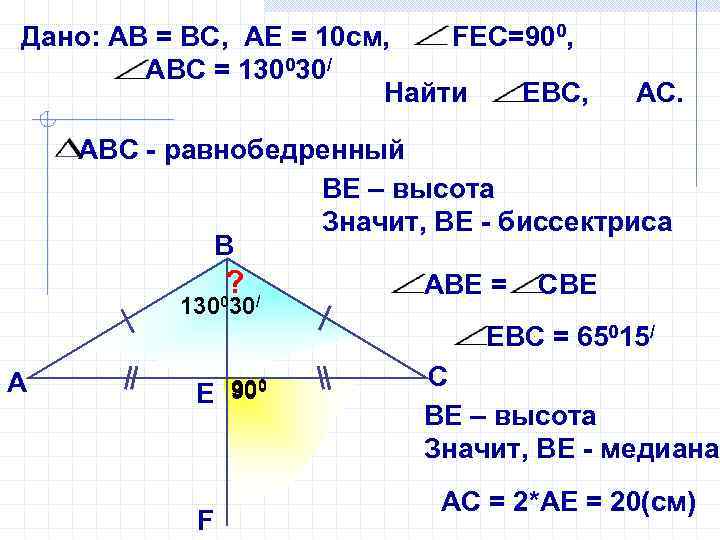
Дано: АВ = ВС, AE = 10 см, FEC=900, АВС = 130030/ Найти ЕВС, АС. АВC - равнобедренный ВЕ – высота Значит, ВЕ - биссектриса В ? / АВЕ = СВЕ 0 130 30 ЕВС = 65015/ А Е 900 F С ВЕ – высота Значит, ВЕ - медиана АС = 2*АЕ = 20(см)
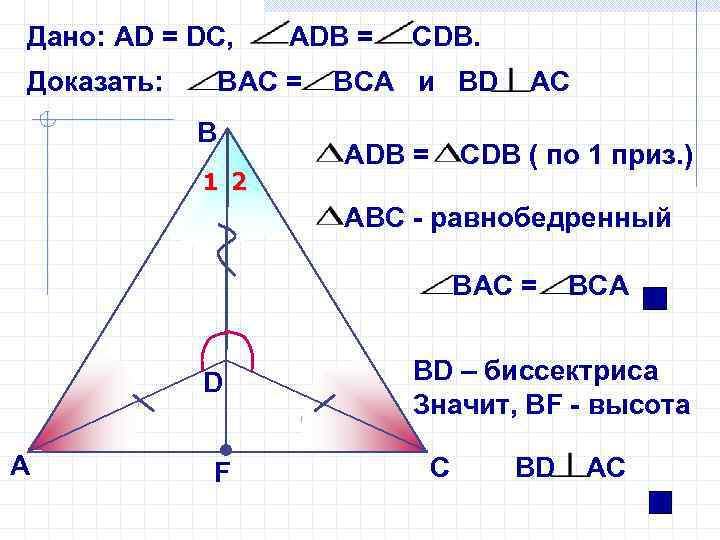
Дано: АD = DС, Доказать: АDB = ВАС = В 1 2 СDВ. ВCА и ВD АDВ = AC СDВ ( по 1 приз. ) АВС - равнобедренный ВАС = D А F ВСА ВD – биссектриса Значит, ВF - высота С ВD AC
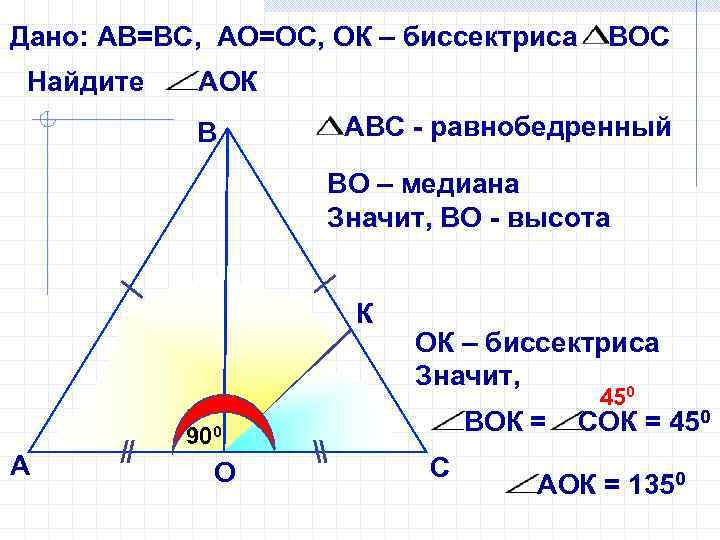
Дано: АВ=ВС, АО=ОС, ОК – биссектриса Найдите ВОС АОК В АВС - равнобедренный ВО – медиана Значит, ВО - высота К ОК – биссектриса Значит, 0 ВОК = 900 А О С 45 СОК = 450 АОК = 1350
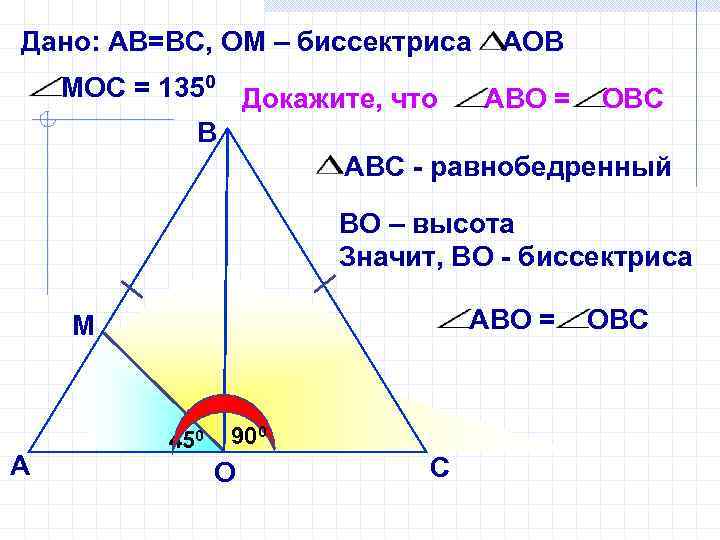
Дано: АВ=ВС, ОМ – биссектриса АОВ МОС = 1350 Докажите, что АВО = ОВС В АВС - равнобедренный ВО – высота Значит, ВО - биссектриса АВО = М А 450 900 О С ОВС
Скачать презентацию А В равнобедренном треугольнике биссектриса проведенная к основанию
10. Равнобедренный треуг. Решение задач.ppt